С переменными во времени параметрами
§ 18.1 Элементы цепей. Электрические цепи с переменными во времени параметрами — это электрические цепи, в состав которых входят резистивные, индуктивные и емкостные элементы, изменяющиеся во времени (если в состав цепи входит хотя бы один изменяющийся во времени элемент, то она принадлежит к рассматриваемому классу цепей).
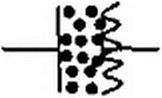
Угольный микрофон — пример изменяющегося во времени резистивного элемента (рис. 18.1, о). Сопротивление его является функцией звукового давления, оказываемого мембраной на порошок графита. Индук-
 |
|
 |
|
 | |||
 | |||
|
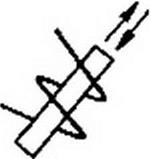
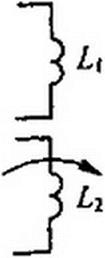
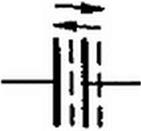
тивная катушка с незамкнутым ферромагнитным сердечником, который выдвигается из катушки и вдвигается в нее (рис. 18.1, б), — пример переменного во времени индуктивного элемента. Конденсатор, пластины которого раздвигаются и сдвигаются, не соприкасаясь (рис. 18.1, в), — пример емкостного элемента, изменяющегося во времени. Две индуктивные катушки Д и 12 (Рис- 18.1, г), взаимное расположение которых меняется во времени (например, если одна из них вращается вокруг своей оси, перпендикулярной рисунку), — пример взаимной индуктивности, меняющейся во времени.
Изменение параметров цепи во времени может происходить под действием внешней механической силы или чисто электрическим путем.
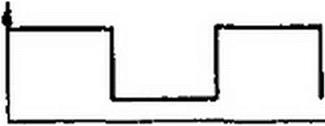
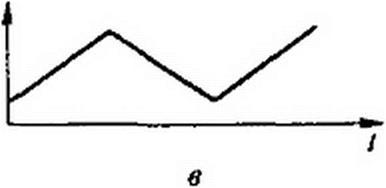
Параметр цепи может изменяться во времени периодически и непериодически. Рис. 18.2, a-в иллюстрирует несколько различных периодических законов изменения параметров.
 |
|
 | |||
 | |||
|
 |
§ 18.2 Общие свойства электрических цепей. Несмотря на то что цепи с переменными по времени параметрами являются линейными цепями (описываются линейными дифференциальными уравнениями), они обладают свойствами, сближающими их с нелинейными цепями.
Переменные во времени элементы цепи, подобно нелинейным элементам, являются генераторами высших гармоник тока и напряжения. В силу этого в цепях с переменными параметрами протекают токи не только тех частот, которые имеют источник вынуждающей силы и переменная составляющая изменяющегося во времени параметра, но и токи множества других частот.
Благодаря этому в цепях с переменными параметрами при наличии в их составе индуктивных и емкостных элементов могут возникать резонансные явления на высших и низших гармониках при отсутствии гармоник данной кратности у источника ЭДС.
Обратим внимание на то, что амплитуды отдельных гармоник тока в цепях с переменными параметрами линейно зависят от амплитуд остальных гармоник (в нелинейных цепях аналогичная зависимость нелинейна).
Наряду с этим цепи с переменными во времени параметрами обладают линейными свойствами, принципиально отличающими их от нелинейных цепей. В них амплитуды гармоник тока и напряжения пропорциональны амплитуде вынуждающей силы. Другими словами, если ЭДС
 источника увеличить вдвое, то и амплитуды токов и напряжений увеличатся вдвое. В цепях с нелинейными элементами, где имеет место насыщение, такой пропорциональности, как известно, нет.
источника увеличить вдвое, то и амплитуды токов и напряжений увеличатся вдвое. В цепях с нелинейными элементами, где имеет место насыщение, такой пропорциональности, как известно, нет.
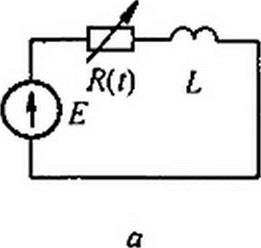
Ранее отмечалось, что изменяющиеся во времени элементы цепи являются генераторами высших гармоник, Убедимся в этом на простейшем примере. На рис. 18.3 изображена схема, состоящая из источника
постоянной ЭДС Е и резистора R, сопротивление которого изменяется во времени в соответствии с кривой (рис. 18.2, б):
 R(t)~ Rq (1 - к sin coz), А<1.
R(t)~ Rq (1 - к sin coz), А<1.
По закону Ома, ток в цепи
 | |||
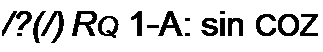 | |||
Известно, что функция 1/(1 -х) при |х|<1 может быть разложена в степенной ряд:
(18.3)
Роль, которую играет х в (18.3), в (18.2) выполняет к sin со t. Поэтому при к < 1
—-— = 1 + к sin a>t + к~ sin2 со / + к3 sin3 со/ + .... (18.4)
Е/Яо
Воспользуемся известными из тригонометрии формулами:
sin2 а = 0,5 (1-cos 2 а), sin3 а =-0,25 sin За+ 0,75 sin а,
sin4 а =0,375-0,5 cos2a + 0,125 cos4a
и объединим слагаемые правой части ряда (18.4) с аргументами одинаковой кратности. В результате получим
= (1 + 0,5 к1 + 0,375 к4 +...) + (к + 0,25 к3 +...) sin со / - Е//?о
- (0,5 к2 + 0,5 к4 +...) cos 2 со t -(0,25 к3 +...) sin 3со/.
Таким образом, несмотря на то что в цепи (рис. 18.3) включен источник постоянной ЭДС, а переменная составляющая сопротивление резистора изменяется по закону синуса с частотой со, ток имеет и высшие гармоники (частоты 2со, Зсо). Постоянная составляющая и амплитуды гармоник тока нелинейно зависят от коэффициента к, но линейно зависят от ЭДС Е.
Обратим внимание также на то, что при к * 0 постоянная составляющая тока в цепи (рис. 18.3) не равна т. е. в схеме наблюдается своеобразный выпрямительный эффект.
Энергия, выделяющаяся в виде теплоты в цепи с переменными во времени параметрами, доставляется не только источниками ЭДС (тока), имеющимися в цепи, но и теми внешними источниками (например, механическими двигателями), которые совершают работу при изменении параметра (параметров) цепи.
Какую долю энергии доставляет источник ЭДС, а какую дает внешний источник, совершающий работу при изменении параметра, для каждой цепи с переменными параметрами следует рассматривать применительно к конкретным условиям. Доля энергии, доставляемая внешним источником, может составлять в одном предельном случае нуль, в другом — 100%.
Отметим различие в определении напряжения от тока или тока от напряжения для элементов одинаковой физической природы для двух случаев:
§ 1.1 да величина, характеризующая этот элемент (сопротивление, индуктивность, емкость), является функцией времени;
§ 1.2 да она является нелинейной функцией тока или напряжения на нем.
Для резистивного элемента в первом случае uR = R(t) i, во втором — «Л=^(0-
Для индуктивного элемента в первом случае потокосцепление
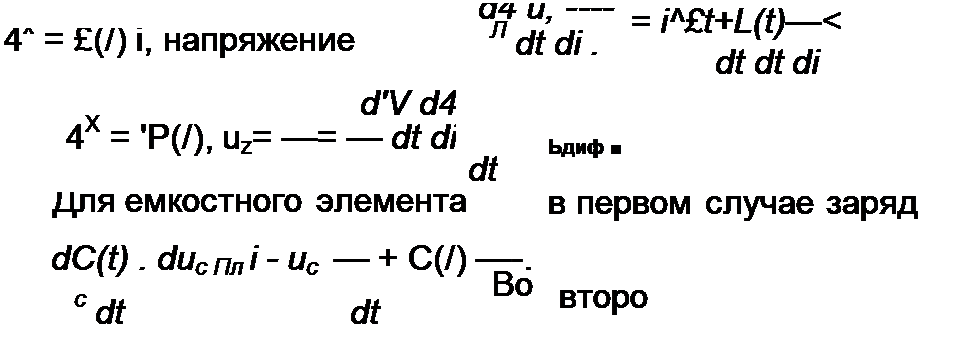 | |||||
 | |||||
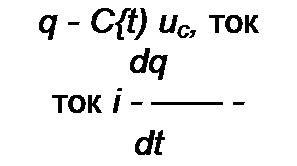 | |||||
dq(uc) duc 4 duc
duc dt диф c dt ’
§ 1.3 Расчет электрических цепей в установившемся режиме. Если переменный параметр изменяется во времени периодически, претерпевая резкие скачкообразные изменения (см. рис. 18.2, а), то расчет цепей целесообразно проводить с помощью классического метода расчета переходных процессов. В этом случае постоянные интегрирования определяют исходя из законов коммутации и периодичности процесса.
Если же переменный параметр изменяется так, что его можно представить в виде постоянной составляющей и одной или нескольких синусоидальных составляющих, то расчет производят, применяя метод гармонического баланса.
Метод гармонического баланса применительно к нелинейным цепям был рассмотрен в § 15.46. Основные его положения и здесь те же. Последовательность расчета такая: искомый ток (любая другая величина) изображают в виде ряда Фурье
i = /0 + /jj sin со/ + /12 cosco/ + /21 sin 2со г + /22 cos2©/ + ....
Полученное выражение для тока подставляют в дифференциальное уравнение цепи и выделяют из него уравнение, выражающее собой равенство постоянных составляющих левой и правой его частей, уравнение, выражающее собой равенство синусных составляющих левой и правой частей, и т. д. Каждое из этих уравнений в общем случае содержит несколько неизвестных (/0, /п, /12, /21, /22), н0 является линейным уравнением относительно этих неизвестных (в этом отличие от нелинейных цепей). Далее решают систему линейных уравнений относительно Л» Ап Аг» ^21» Лг-
Метод гармонического баланса можно применять к расчету цепей, содержащих несколько переменных во времени параметров (например, изменяющееся во времени резистивное сопротивление и изменяющуюся во времени индуктивность), причем характер изменения во времени ЭДС (тока) может быть по любому периодическому закону.
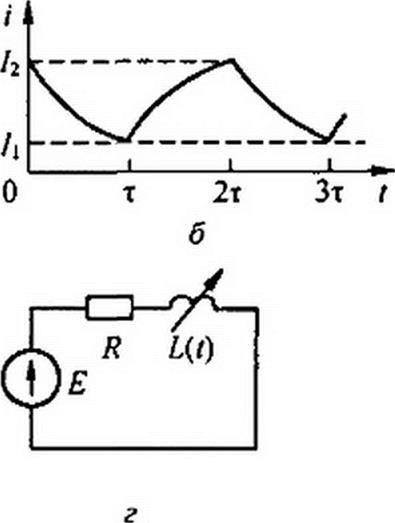
Пример !67. В схеме на рис. 18.4, а ЭДС Е источника ЭДС и индуктивность L катушки постоянны, а сопротивление резистора R(f) меняется в соответствии с рис. 18.4, в. Определить закон изменения тока в установившемся режиме.
| R |
| Я. |
| Ri |
| Рис. 18.4 |
| Решение. Так как сопротивление изменяется периодически, то и ток изменяется периодически. Обозначим значение тока в момент / = О через /2. В этот момент сопротивление цепи скачком возрастает от Л2 до /?, и ток в цепи начинает уменьшаться. В момент t = х ток принимает значение /] и сопротивление скачком уменьшается с Rt до R2. Последнее приводит к тому, что ток начинает увеличиваться. В первом интервале времени от / = 0 до t = т ток можно представить в виде суммы принужденного E/R} и свободного С, e/J|' токов, причем p\=-RjL —корень характеристического уравнения цепи р L + R} =0; С( — постоянная интегрирования. Во втором интервале времени от / = т до г = 2 т |
| *2 |
| /?2 ; р2=—г |
| Задача сводится к определению двух постоянных: С] и С2. При / = 0 i = /2; следовательно. |
| (18.5) |
| При t = Q /=/|, поэтому |
| (18.6) |
| Начальное значение тока для второго интервала времени /, можно найти и иначе: |
| _Е /?■ |
| (18.7) |
| К концу второго интервала времени, когда <= 2 т, i- 12 |
| Р2 * |
| /?2 Приравнивая правые части уравнений (18.5) и (18.8), получим |
| (18.8) |
| Л| |
| Аналогично из уравнений (18.6) и (18.7) следует, что |
Совместное решение двух последних уравнений дает
 С а^~сРг х).
С а^~сРг х).
’ |_еРП«ФН’
С2 — ~о + С| е;1 т; а = ————.
Л2 Л,
В первом интервале времени
i^EjRi +С| ел\
во втором
i-E/R2 + С2 с7’2 ('-х).
Кривая / = /(/) показана на рис. 18.4,6.
Пример 168. В схеме на рис. 18.4, г ЭДС е = Е + Е„, sin(o>/ + \j/), L = Z-o (1 + к sin to /) (к < 1), сопротивление R не является функцией времени. Определить постоянную составляющую, а также первую и вторую гармоники тока.
Решение. В дифференциальное уравнение
 R i +—(L /') = Е + Ет sin(w t + ф)
R i +—(L /') = Е + Ет sin(w t + ф)
подставляем ток
i = /0 + /ц sin со / + /]2 cosw / + /21 sin 2 о/ + /22 cos 2 со/. (18.12)
Выделив постоянную составляющую, получим уравнение
RIq-E. (18.13)
Равенство коэффициентов при sin со/ в обеих частях (18.11) после подстановки в него (18.12) и деления на R дает
 /п -а /12 “0,5 к а /2! = —— совц/.
/п -а /12 “0,5 к а /2! = —— совц/.
R
Приравняв коэффициенты при cosw/ (после деления на /?), получим
£ а /)! + /12 - 0,5 к а /22 = -а к /0 + ——sin ц/;
R
при sin2со/
а А /1( +/2) - 2 о /22 = 0;
при cos2со/
Q к /]2 + 2 а !2\ + 1= 0’
о — со Z.q ] R .
Из (18.13) следует, что в схеме на рис. 18.4, г постоянная составляющая тока 1q не зависит от переменных составляющих индуктивности и ЭДС. Однако постоянная составляющая потокосцепления, равная Lq /о +0,5 A Lo /и, зависит от амплитуды первой гармоники переменного тока.
Это свойство в известном смысле напоминает первое из свойств нелинейных элементов с симметричными характеристиками, описанное в § 15.17.
Запишем решение уравнений (18.14)-(18.17):
Л1 - 2 л2~' ------------------ ’ ^21 “ 7 Л1 ” v Лз» ^22 = v Л I “ 7 ^)2 >
а+(3 а
.. Ет К, • , , 1 + 4 а2 -0,5 а2 к2
М = —— cosvp; /V = —sin у - а Wo; а =---------------------------- ---------------------------------------------------------------------------------- --------------------------------------------------------------------------------- ;
Я R 1 + 4 а2
ак о а(1 + 4а2-а2 к2) 2а2 к
7= , , ,; Р = —------------------------- 5--------- ; v =------------- г-
1+4а2 1 + 4а2 1 + 4а2
Изменяя постоянную ЭДС £ в схеме на рис. 18.4, г, можно управлять переменным током.
§ 1.4 Параметрические колебания. Возникающие в электрических цепях без источников ЭДС и источников тока незатухающие колебания, обусловленные периодическим изменением индуктивности или емкости системы, называют параметрическими. Колебания поддерживаются за счет работы механической силы при периодическом изменении параметра либо за счет энергии, вносимой в цепь при периодическом изменении параметра электрическим путем. Частота первой гармоники параметрических колебаний оказывается в два раза меньше частоты изменения параметра.
На рис. 18.5, а изображена простейшая цепь, в которой при определенных условиях возникают колебания рассматриваемого типа. Цепь состоит из катушки индуктивностью L, нелинейного резистора, ограничивающего амплитуду колебаний /?(/) = Rq + к i2,
 | |||
 | |||
| ||||
| ||||
и конденсатора, емкость которого изменяется во времени: С = Со - AC cos2 (at, ЬС[С§ <к 1, (Предположение, что <к I, принято только для облегчения решения.)
Сначала рассмотрим случай, когда емкость конденсатора изменяется механическим путем.
Внешняя сила, совершающая работу при изменении емкости конденсатора, доставляет в цепь энергию. Эта энергия равна потерям в активном сопротивлении. По второму закону Кирхгофа,
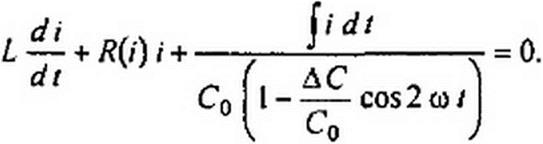 |
В соответствии с формулой (18.3) последнее слагаемое представим так:
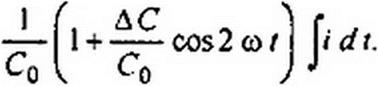 |
Подставим в это уравнение i -a sin со t-b coscat, разобьем его на синусные и косинусные составляющие частоты со (высшими гармониками пренебрежем) и решим отно-
сительно квадрата амплитуды тока а2 +Ь2 = А2:
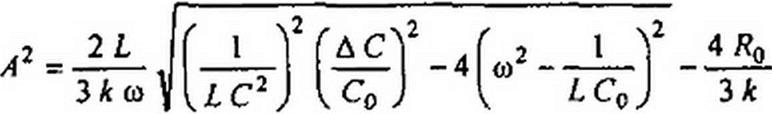 |
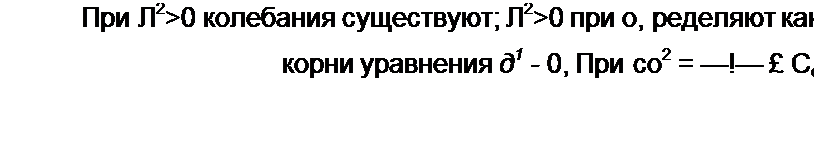 | |||||
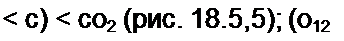 | 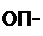 | ||||
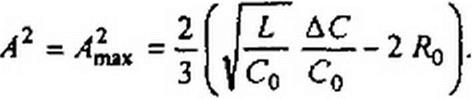 |
Условием возникновения колебаний в этом случае является
ДС 2/?0 "Ч-1Ч- ■ Q VZ/cT
Качественно поясним сущность процесса поступления энергии в цепь при изменении емкости конденсатора во времени. Энергия, запасенная в электрическом поле конденсатора емкостью С с зарядом ±д на пластинах, = $2/(2С). Если при неизменном q емкость изменить на ДС (ДС/С « 1), то энергия станет равной
2(С + ДС) 2С< С)
Приращение энергии
Верхняя кривая на рис. 18.5, в изображает изменяющийся по синусоидальному закону во времени заряд q. Средняя кривая иллюстрирует характер изменения емкости во времени (для простоты рассуждений он принят не синусоидальным, а прямоугольным). Когда заряд q проходит через максимум, то емкость почти скачком уменьшается (ДС <0), когда через нуль, то емкость почти скачком возрастает (ДС > 0).
Уменьшение емкости соответствует раздвиганию пластин конденсатора, а увеличение — их сближению. Поэтому, чтобы при q~q„ емкость почти скачком уменьшить, нужно быстро раздвинуть пластины. Но пластины заряженного конденсатора притягиваются друг к другу. Следовательно, для того чтобы раздвинуть пластины, внешний источник энергии должен затратить работу на преодоление сил их притяжения. Эта работа переходит в энергию электрического поля конденсатора. За период изменения q энергия конденсатора дважды возрастает на величину
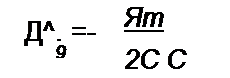 |
Сближение пластин (увеличение С) происходит при q = 0, когда силы, действующие на пластины (силы поля), равны нулю. Поэтому при сближении пластин внешняя сила не совершает работы.
Поступление энергии в параметрическую цепь при изменении параметра цепи называют накачкой энергии. Рис. 18.5, в качественно поясняет также, почему частота колебаний на схеме в рис. 18.5, а в два раза меньше частоты изменения параметра (емкости). Если емкость стала бы изменяться во времени в соответствии с пунктирной кривой (рис. 18.5, в), то энергия в этом случае в цель не доставлялась бы (не накачивалась), ибо сколько энергии доставит в цепь внешний источник при уменьшении емкости, столько же цепь отдаст ему обратно при ее увеличении. Накачка энергии в цепь может происходить не только при изменении емкости, но и при изменении индуктивности во времени.
§ 1.5
 |
|
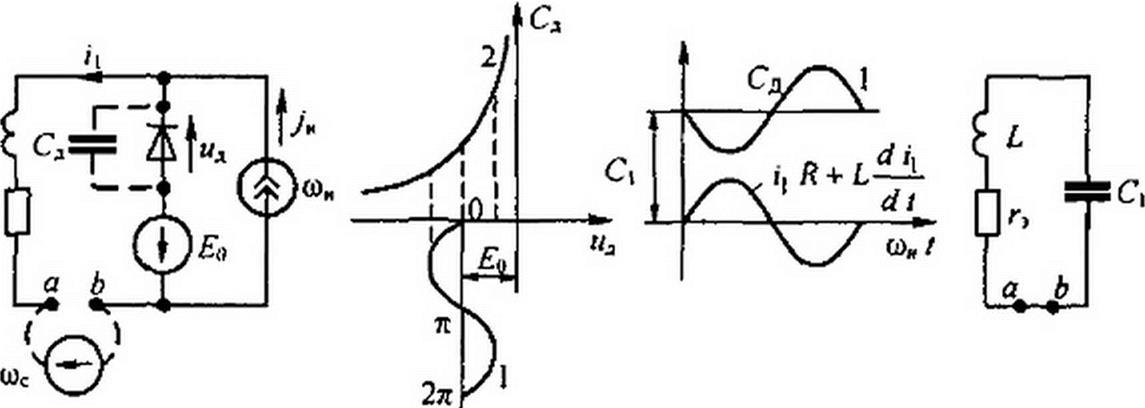
Параметрические генератор и усилитель. В параметрических генераторе (ПГ) и усилителе (ПУ) емкость варьируют не механическим, а электрическим путем — изменяя емкость диода (варикапа), находящегося в запертом состоянии. На рис. 18.6, а в ПГ зажимы ab закорочены, а в ПУ к зажимам ab подключен источник сигнала частотой ос (показано штриховой линией). Источник постоянной ЭДС Ео запирает диод.
«и г
Накачка энергии осуществляется от источника синусоидального тока jH частотой о)н и амплитудой /нот. Часть этого тока (ток /,) амплитудой /,да проходит через Л и £ и совместно с Ео образует падение напряжения на диоде:
и д = -£о -£'| ~£'7Т al
(кривая 1 на рис. 18.6, б). Чтобы диод был заперт, это напряжение должно быть отрицательным. Диод будет заперт, если
Зависимость емкости р—л-персхода Сд‘' от напряжения на диоде дв иллюстрируется кривой 2 (рис. 18.6, б). а изменение емкости Сд во времени — кривой / (рис. 18.6, в). Среднее за период значение емкости Сд обозначим С,.
Схема замещения параметрического генератора для частоты параметрических колебаний о>р = (он/2 * 1 //l С| изображена на рис. 18.6, г. Вносимая генератором накачки (источником синусоидального тока) на частоте t>H энергия компенсирует потери в активном сопротивлении R на частоте wp. Этот процесс можно трактовать как уменьшение активного сопротивления колебательного контура г3 до нуля (ср. с ламповым генератором § 16.6, в котором = R- М S/С). Амплитуда установившихся колебаний определяется энергетическим балансом.
Если допустить, что глубина модуляции емкости Сй т I, то, составив дифференциальное уравнение для колебательного контура LRCa (зажимы ab на рис. 18.6, а короткозамкнуты);
Ri + L + — Г л dt = O
dt Cj 1
‘‘При ил <0 основную роль играет барьерная емкостьр—и-перехода, обусловленная перераспределением зарядов у границы областей с различным характером проводимости. При > 0 основную роль играет диффузионная емкость р—и-перехода. Она обусловлена перераспределением зарядов в базе. В схеме на рис. 18.6. под Сд поднимается барьерная емкость.
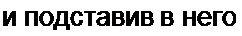 | |||||||
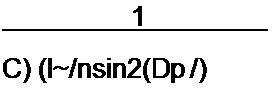 | |||||||
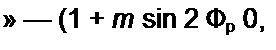 |  | ||||||
получим два уравнения (синусная и косинусная компоненты):
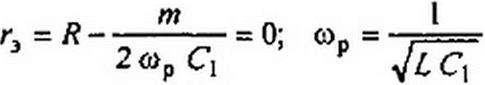 |
При работе схемы (см. рис. 18.6, а) в качестве ПУ генератор накачки настраивают на такой режим, при котором вносимая им энергия уменьшает активное сопротивление контура г, не до нуля (как это было в случае с ПГ), а до г, « R. Параметры Ln С, подбирают так, чтобы фс = 1 С) . При этом источник сигнала (источник ЭДС fc частотой фс) вызовет ток /с=—.
гэ
 Отношение выходного напряжения (на индуктивном элементе) к входному достаточно велико — схема работает в качестве усилителя.
Отношение выходного напряжения (на индуктивном элементе) к входному достаточно велико — схема работает в качестве усилителя.
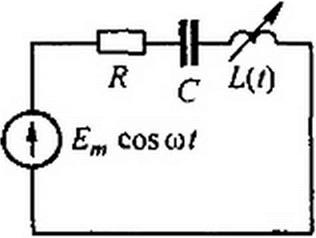
§ 1.6 Исследование устойчивости периодических режимов работы линейных электрических цепей с переменными во времени параметрами. Методику рассмотрим на примере цепи на рис. 18 .7, а, содержащей источник синусоидальной ЭДС Ет cos&i. резистор /?, конденсатор С и изменяющуюся во времени индуктивность L(t) = Lq (I - т cos 2 cut), полагая, что т « 1.
 | |||
 | |||
| ||||
| ||||
 |
Составим уравнение по второму закону Кирхгофа для электрического заряда q конденсатора в периодическом режиме работы, имея в виду, что ток i = dq/ dt, напряжение на конденсаторе и(;=$/С, а потокосцепление индуктивности равно произведению £(/) di
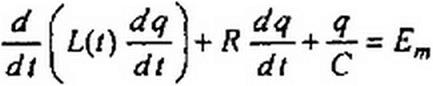 |
|
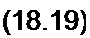 |
Первое слагаемое уравнения (18.19) заменим двумя слагаемыми:
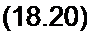 ,, . d2q dl(t) dq ndq q _
,, . d2q dl(t) dq ndq q _
4(z) —+ —— — + /? ~г + ~: = Em со$фл
dt1 dt dt dtC
Затем объединим два слагаемых с первой производной dqldt и придем к уравнению (18.21):
,.,'d2q (о dL{t)\dq 1 г
L(z)72+ я + + = COS(OZ
dr \ dt J di C
Поделим уравнение (18.21) на L(t}:
2
d q dt dq I _ £„ costo/
Ti2* L{() ~di + L{t}'cq~ L(t)
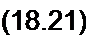
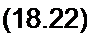 Положим, что заряд q получил малое приращение д<? и стал равен <? + △?. Составим уравнение движения для возмущенного состояния:
Положим, что заряд q получил малое приращение д<? и стал равен <? + △?. Составим уравнение движения для возмущенного состояния:
R , dL(t)
+ = (18 23)
dt2 L(t) dt L(t)C * L(t)
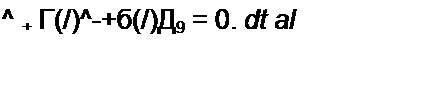 | |||||
 | |||||
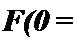 | |||||
|
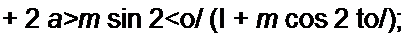 | |||||||
 | |||||||
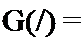 | |||||||
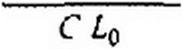 | |||||||
|
 | ||||||||||||||||
 | ||||||||||||||||
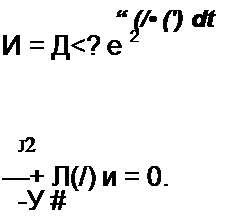 | ||||||||||||||||
 | ||||||||||||||||
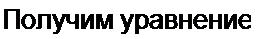 | ||||||||||||||||
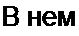 | ||||||||||||||||
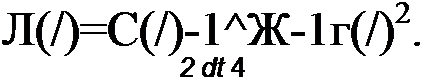 | ||||||||||||||||
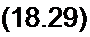 | ||||||||||||||||
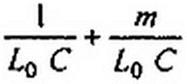 | ||||||||||||||||
 | ||||||||||||||||
|
 |
|
|
Вычтем из уравнения (18.23) уравнение (18.22). Получим уравнение (18.24) для приращения заряда Д^:
В уравнении (18.28) от времени / перейдем к безразмерному времени т = со/, домно-
*2П to2 2
жив ,2 на и поделив затем все уравнение на со . Получим уравнение, называе* а' со
мое уравнением Матье:
d2x\
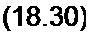 —+ 16 6 cos2t) т| = 0. dx1
—+ 16 6 cos2t) т| = 0. dx1
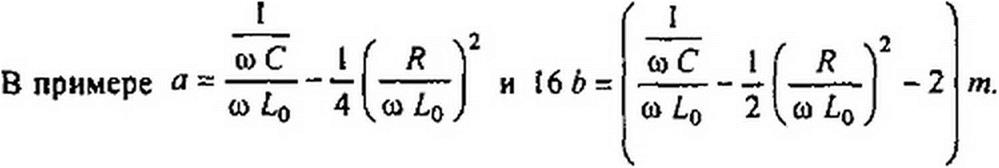 |
|
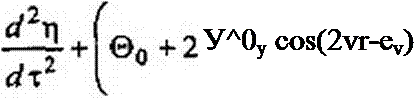 | |||
 | |||
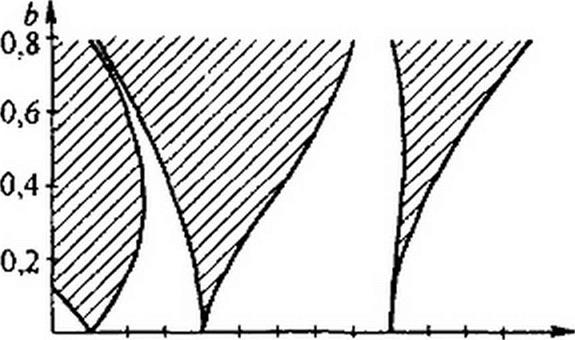
®о и 0V — некоторые числа. Периодический режим работы схемы рис. 18.7, а окажется неустойчив, если малое приращение Zty будет стремиться неограниченно возрастать во времени. Если уравнение для приращений может быть сведено к уравнению Матье, то устойчивость периодического процесса к малым возмущениям в линейных цепях с переменными во времени параметрами определяют с помощью семейства кривых рис. 18.7, б, построенных на основании теории функций Матье.
Решение уравнения Матье может быть записано в виде:
П = С, едТф(т) + С2е и*ф(-т).
Здесь С;,Сг — постоянные; и — характеристический показатель, являющийся действительным или мнимым числом; ф(т) — периодическая функция по t или 2 т. Решение неустойчиво, если g действительно, и устойчиво, если ц мнимое.
Периодическое решение уравнения Матье записывают с помощью функций Матье. При малых b функции Матье представляют собой ряды по степеням Ь, умноженные на синусы и косинусы аргументов, кратных т. Уиттекером*’ вычислены собственные значения параметров**’, соответствующих функции Матье ас„ и а#, (w = I + 3).
Зависимости собственных значений параметров функций ас„ = /(б) и as>, = /(b) при трех значениях п, являющиеся граничными кривыми для трех областей неустойчивости (они заштрихованы), построены в прямоугольной системе координат а и Ь на рис. 18.7. б. Кривые исходят из точек на оси абсцисс, для которых а ~ 1, 4,9. Если при некоторых значениях коэффициентов а и b в уравнении Матье изображающая точка на рис. 18.7, б окажется в какой-либо из заштрихованных областей, то периодический режим работы окажется неустойчив к малым возмущениям. Физически это объясняется тем, что энергия, доставляемая в цепь источником ЭДС и модулятором индуктивности, будет превышать тепловые потери в резисторе. В тех случаях, когда уравнение для приращения не может быть сведено к уравнению Матье, необходимо будет обратиться к уравнению Хилла. Однако исследование устойчивости в этом случае существенно усложняется (см. книгу Уиттекера и Дж. Н. Ватсона, книгу Т. Хаяси [32] или книгу В.А. Тафта «Электрические цепи с переменными параметрами» (М.: Энергия, 1968).
§ 18.7. Исследование устойчивости периодических режимов работы нелинейных электрических целей переменного тока с помощью функций Матье. На рис. 18.8 изображена электрическая цель, содержащая источник синусоидальной ЭДС Е„ sin(co I + у),
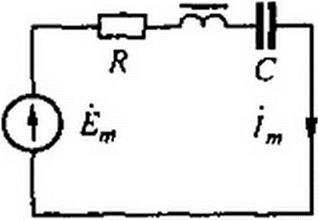
|
нелинейную индуктивность НИ, вебер-амлерная характеристика которой описана формулой / = ashp\p, конденсатор емкостью С и резистор R (схема ранее была рассмотрена в § 15.58; она при определенных соотношениях параметров имеет У-образную ВАХ). В установившемся режиме работы при потокосцеплении ц/ = %, sin а>1 первая гармоника тока в цели sin<oz = 2 a (-J Jj (у Р Ч'да)) sin со/. Если потокосцепление V
получит малое приращение Дф, то ток в цепи станет равным z = ash(P <Р„ sin со/+ Др Y).
*' Уиттекер Э.Т., Ватсон Дж. Н. Курс современного анализа. — М.: Физматгиз, 1961.
“’Под собственными значениями параметров, соответствующих функциям аС)1 и понимают значение а при заданном значении Ь.
| Но |
| sh(p4/m sin о/ + Др Тд,) - sh(P 'Нд, sin (оО ch др Т + ch(p'K/n sin cor) sh Др *F. |
| Учтем, что |
| sh(p Wn sin co/) s 2 (~y Jj(JP Tw))sin<o/, |
| ch(P %, sin co/) * J0(y P Ч'д,) + 2 J2(y p ) cos 2co/ |
| (см. формулу 15.10). При Д0 Ч" <к I ch Др Ч' = l, 5ЬДРЧ'*ДРЧ/. Приращение тока Д/ = a (J0{J p ) + 2 J2(j p У,, ) cos2co/) Др У. (18.31) Составим уравнение для схемы рис. 18.8 для получения приращения дрч7: sinco/+/?/ + ^ рс// = £„ sin(to/ + y) |
| и уравнение после возникновения возмущения: |
| ------ (Р Ч'д, sin со/ + Др Т)+ R (f + Д/) + J(/ + Д/) dt - Ет sin(co/ + у). |
| Вычтем из второго уравнения первое, получим уравнение для приращения (18.32) |
| 1^Р+Дд, + ±и,Л = 0. р dt С J |
| (18.32) |
| подставим в него Д/ из (18.31). обозначим со/ = т, домножим полученное выражение на —. а подынтегральное выражение еще на —, и продифференцируем все уравнения по т. 0) <0 Получим дифференциальное уравнение второго порядка в безразмерных единицах: |
| f^±+r,W^*+C|(t)A₽T = 0. dx2 dx |
| (18.33) |
| Здесь F\ (т) = Wj р %,) + 2 J2 ( j Р ) cos 2 т), (0 Gi(t) = UoO P ) + 2 J2(j p ^) cos21) -J2(j p 'Кд,) sin2t. (£>- С О |
| Как и в § 18.6 устраним первую производную в (18.33), воспользовавшись подстановкой (18.27), и придем к уравнению: |
| ^~- + Л[(т)П| =0. dxi |
| (18.34) |
| Л) (т) = j,(y р ) Sin2 г + 0 П,) + 2Уг(/ р ) cos2х) - О 0)- С ~И—"I f7o(7P^) + 4J0Op4>n,)J:(yp4>m)cos2t + 4J,2(7p4>m}i(l + cos4x)l 4 V о Л 2 / |
| При |
| 1 Я2 ар 2 to С 4 со |
| JoU’P%») 1 уравнение (18.34) является уравнением Матье, |
в котором в данном случае
2 / .
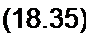
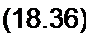 О = АО Р %,>-(— ] (4(/ Р %,) * 14(/ р S',) );
О = АО Р %,>-(— ] (4(/ Р %,) * 14(/ р S',) );
от2 С V ю J к 2 )
16 b = J2 (jр р0 (/ р Ч-„) J2 (J 0 Т„).
(О2 С \ G> J
Далее учтем следующее.
L Энергия на возрастание возмущения в линейной и нелинейной цепях, рассмотренных выше, доставляется в цепь от разных источников. В первом случае от внешнего источника модуляции и от синусоидального источника, во втором — от синусоидального источника питания схемы. Кроме того, в линейном случае уравнение составлено относительно а в нелинейном — относительно Это привело к тому, что знаки коэффициента b в уравнении Матье в этих двух случаях различны: в линейном случае b > 0, в нелинейном— д<0 (так как J2(/AP<F)<0.
2. В нелинейном случае коэффициент а может принимать значения от 0 до 2,2, а коэффициент | b | — от 0 до - 0,2. В линейном случае при Ь > 0 в этом диапазоне изменения а и b левая кривая первой области неустойчивости рис. 18.7, б описывается функцией ас1 = 1 - 8 6, а правая кривая — функцией дт1 = 1 + 8 b (см. § 3.6 [32]). Изменение знака коэффициента Ь в нелинейном случае по сравнению с линейным при b > 0 приведет к тому, что в указанном диапазоне изменения а и b левая кривая рис. 18.7, <5 будет описываться функцией ал1, а правая — функцией od, сама же первая область неустойчивости останется неизменной и ею можно пользоваться и при b < 0, откладывая по оси ординат модуль Ь.
3. Физически неустойчивость работы на падающем участке ВАХ цепи рис. 18.8 объясняется тем, что флюктуация Др 4х приводит к появлению постоянных составляющих и второй гармоники в токе и магнитном потоке НИ. Нелинейное взаимодействие первой и второй гармоник потока, зависящее от их амплитуд и фаз (см. § 15.18), приведет к росту «постоянной» составляющей потока и возникновению отрицательной дифференциальной индуктивности НИ по «постоянным» составляющим потокосцепления и тока.
Рассмотрим пример. Вебер-амперную характеристику НИ схемы рис. 18.9 для мгновенных значений величин опишем формулой:
i = ashpy = 0.0067 sh 62.8 %
угловая частота со = 314с‘’. R - 10 Ом, С = 73.6 мкФ. ВАХ НИ по амплитудам первых гармоник Um-f(Im\ где
= 5р%„
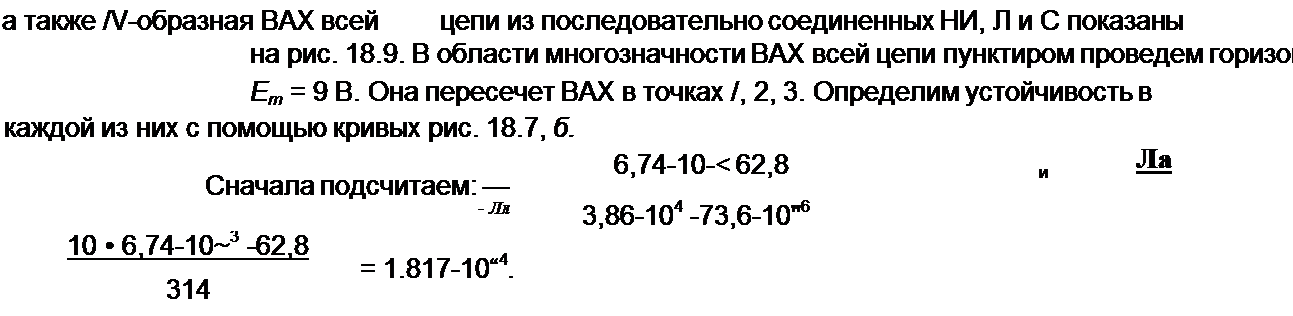 |
В точке / рис. 18.9 Р = 2, Jo<2 Р = 2,28, J2(j Р 4>w) = -0,69; а, = 0,1322, by = -0,005.
Точка а,, | Ьу | на рис. 18.7, б находится в незаштрихованной области — режим устойчив.
| P Vw U т> В |
| 32 - |
| 0 0 0,1 0,2 0,3 0,4 0,5 0.6 0,7 0,8 0,9 J.O |
| Рис. 18.9 |
| В точке 2 рис. 18.9 =4,6, J0(j р V,„) = 19,01, Jz(j Р ) = -11,71; д> = 1,036, b\ = -0.083. Точка а2,|/>21 на рис. 18.7, 6 оказалась в заштрихованной области — режим неустойчив. В точке 3 Р^, =5,3, Jo(; Р %,,) = 23,65, J2(; Р =-15,6; а, = 1,798. di = -0,163. Точка а3,|6} 5 на рис. 18.7. б находится в незаштрихованной области — режим ус- тойчив. |
| Вопросы для самопроверки |
| I. Почему можно сказать, что линейные электрические цепи с изменяющимися во |
| времени параметрами занимают промежуточное положение между линейными цепями с неизменными параметрами и нелинейными электрическими цепями? 2. Какие вы знаете способы изменения параметров реактивных элементов в изучаемых цепях? 3, Изложите известные вам методы расчета цепей с переменными во времени параметрами. 4. Какие колебания называют параметрическими? 5. Что понимают под накачкой энергии в параметрическую цепь? Как ее осуществляют практически? 6. Чем можно объяснить, что частота изменения параметра в два раза больше частоты параметрических колебаний? 7. Поясните принцип работы параметрического генератора и параметрического усилителя. 8. Электрическая цепь (рис. 18.7, а) образована источником синусоидальной ЭДС е(г) = Ет sin от, резистором R, конденсатором С и индуктивной катушкой, у которой 4(/) = Lq (1 + т sin от). Через £(/) протекает ток i + /0. Приняв i = sin(wT-a): I) по- |
| кажите, что зависимость постоянной составляющей потокосцепления ц/0 индуктивной катушки оттока /0 имеет вид = а + b /0; 2) выведите условия, при которых b < 0 (при |
| < 0). Покажите, что режим работы при этом будет неустойчив. (Ответ: |
| т Lq R Ет |
| 2 «.2 + /?2 — —— (О Lq |
| о ------------ — (£)С |
| 2 о Lo------------ |
| 2) Ь < 0 при выполнении трех условий: |
| 1 Ля2 0 wCj |
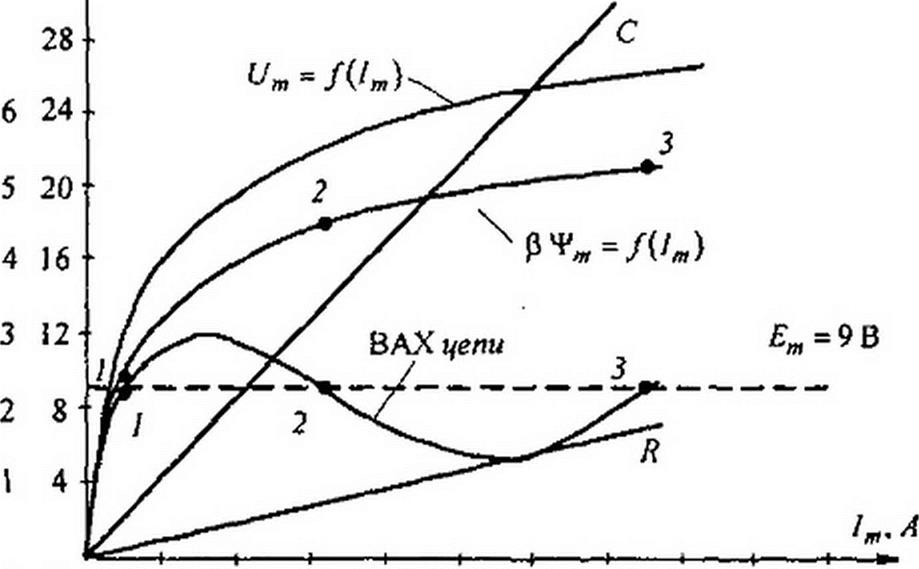
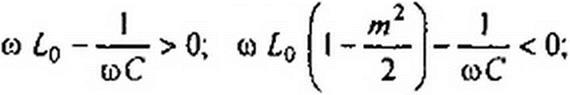
| R2 |
| .) 9. Определите энергию, которая будет введе |
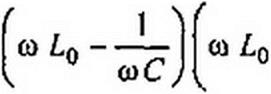
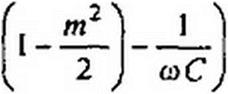
на в цепь рис. 18.7, а при модуляции индуктивности по закону £(/) = L0(\-m cos2<oz) и
2 д
при протекании тока по цепи i - !„ sin(cof - v) за один период Т =--------------------------------------------------------------------------------- . (Ответ:
Г , 2 ю
г AC/') i nt А i
Г--------- di =-------- 2--— sin2v.) 10. Определите, будет ли устойчив периодический режим
*2 4 л
о
работы схемы рис. 18.7, а если 4о=1Гн, С = 0,25 мкФ, R - 2 Ом, т = 0,1, со = 1. 11. Изложите последовательность действий при исследовании устойчивости периодических процессов в линейных электрических цепях с изменяющимися во времени параметрами. 12. Запишите уравнение Матье, поясните, как к нему можно перейти от уравнения для мгновенных значений величин и как можно исследовать устойчивость с помощью кривых рис. 18.7, б. 13. Поясните, почему метод исследования устойчивости периодических процессов в нелинейных цепях переменного тока путем придания небольшого скачкообразного возмущения потокосцеплению или заряду предпочтителен по сравнению с методом придания возмущений амплитудам синусной и косинусной составляющих первых гармоник этих величин (как в § 17.4)? 14. Изложите последовательность действий при исследовании устойчивости периодических процессов в нелинейных цепях переменного тока путем сведения уравнения для приращений к уравнению Матье.
ЛИТЕРАТУРА
Учебники
1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. — 11-е изд. — М.: Гардарики, 2005; Электромагнитное поле. — 9-е изд. — М.: Сардари- ки, 2001.
2. Демирчан КС., Нейман Л.Р, Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: В 3 т. — 4-е изд. — СПб.: СП, 2003.








