Точку т будем называть точкой равновесия. Она определяет режим работы схемы при прохождении по Л и неоновой лампе постоянного тока.

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Убедимся в том, что режим работы, определяемой точкой т, является неустойчивым: достаточно ничтожно малого отклонения от состояния равновесия, чтобы изображающая точка «ушла» из точки т и не возвратилась в нее. В схеме возникнут релаксационные ко­лебания.

Для того чтобы убедиться в неустойчивости состояния равновесия, составим линей­ную схему замещения релаксационного генератора.

Так как HP имеет S-образную ВАХ, то в схеме для исследования устойчивости оно имитироаано (в соответствии с § 17.3) дифференциальным сопротивлением £_ДНф и по­следовательно с ним включенной малой паразитной индуктивностью £_п, зашунтирован- ной резистором сопротивлением /?_доб.

Дифференциальное сопротивление £_днф в точке т пропорционально тангенсу угла а (рис. 17.3, в) и является отрицательной величиной.

Источник ЭДС в схеме замещения (рис. 17.3, г) не включен, так как исследуется по­ведение схемы в режиме приращений по отношению к режиму, определяемому точкой т.

Входное сопротивление схемы в операторной форме относительно точек а и b

7 ( - Р л. Р^п R
?ah \Р) ~ Я_акф + ⁺ R Г ,

‘'аоб К f

Характеристическое уравнение цепи

р (^доб ⁺ ^диф )⁺ Р (^п ⁺ ^доб ⁺ ^диф)^{+ R} ^доб ^диф ) ⁺ ^доб (^ ⁺ ^диф )'

Так как рабочая точка находится на падающем участке ВАХ HP, то R >|Ядиф| ^{и п0}* этому свободный член положителен. Из условия ReZ(j©)>0 при ю-х» следует, что ^доб ^>|^диф|> поэтому коэффициент при р² тоже положителен. Состояние равновесия будет неустойчивым, если коэффициент при р окажется отрицательным, т. е. при

^L A^{R +} Ядоб ^{+ Л}д.<ф)^{+ С R R} n<*> ^диф < 0.

Рассмотрим последовательность смены состояний при релаксационных колебаниях.

Пусть в схеме (рис. 17.3,6) при нулевых начальных условиях замыкается ключ К. Кон­денсатор С начнет заряжаться, и напряжение на нем будет расти (рис. 17.4, а). Так как конденсатор и неоновая лампа НЛ включены параллельно, то в любом режиме работы на­пряжения на них одинаковы. Как только напряжение на конденсаторе возрастает до значения, равного на­пряжению зажигания и₃ неоновой лампы, последняя зажжется и ток в ней возрастет от нуля до i₄ (рис. 17.4, б). Конденсатор быстро разрядится через НЛ, внутреннее сопротивление которой мало по сравнению с сопротивлением R. При этом изображающая точка на ВАХ НЛ переместится из точки 4 в точку /. В точке I напряжение на НЛ равно напряжению ее гашения ц_г, поэтому неоновая лампа гаснет и ток в ней становит­ся равным нулю (точка 2). Далее конденсатор вновь за­ряжается до напряжения НЛ снова зажигается и процесс повторяется.

Траектория движения изображающей точки на рис. 17.4, б образует замкнутую петлю 12341.

Следует подчеркнуть, что если условия возбужде­ния колебаний в схеме выполнены, то амплитуда ко­лебаний напряжения на конденсаторе не зависит от на­грузки R и ЭДС Е, а определяется только напряжени­ями зажигания w, и гашения и_г НЛ. Период колеба­ний равен сумме времени зарядки и разрядки конден­сатора и зависит от ЭДС Е, емкости С, сопротивления и внутреннего сопротивления НЛ. Обратная связь в схеме находит свое выражение в том, что конденсатор управляет режимом работы НЛ.

В заключение заметим, что если в схеме на рис. 17.3, б ЭДС Е и сопротивление R взять такими, что ВАХ резистора сопротивлением R пересечет ВАХ HP с S-образной характе­ристикой в трех точках (/, 2, 3 на рис. 17.3, д), то точки / и 3 будут соответствовать ус­тойчивым состояниям, а точка 2 начиная с некоторого значения С — неустойчивому.

§ 1.7 Исследование устойчивости периодического движения в ламповом гене­раторе синусоидальных колебаний. Рассмотрим вопрос об исследовании устойчивости синусоидальных колебаний в ламповом генераторе (рис. 16.5). С этой целью воспользу­емся формулами (16.25) и (16.30).

В соответствии с (16.30) производная от амплитуды колебаний

~ _s А(а) = 0.5 а (1-0.25 а²) dt

В установившемся режиме работы амплитуду колебаний обозначим а₀. Для опреде­ления а₀ приравняем da/dt нулю и решим уравнение 1-О,25<?о = 0- Отсюда а₀ = 2.

В соответствии с § 17.4. исследования устойчивости периодического движения a sin о/ а автоколебательной системе, на которую не воздействует внешняя периодическая сила частотой ел, достаточно найти знак производной dA(a)/da при a = a_Q. Если при этом d A{a)/da< 0, то процесс устойчив. В нашем случае

{ d Л(а)^

Ранее (см. уравнение (16.27)) было выяснено, что a' М > RC и к_} > 0, так как толь­ко в этом случае амплитуда колебаний представляет собой вещественную величину. Сле-

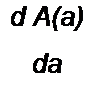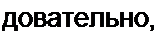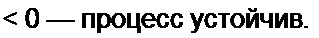§ 1.8 Исследование устойчивости работы электрических цепей, содержащих управляемые источники напряжения (тока) с учетом их неидеальности. Прежде чем приступить к исследованию устойчивости той или иной схемы, надлежит проверить, нет ли в схеме ОУ, у которого имеется обратная связь с выхода на его положительный вход, а минусо­вой вход ОУ заземлен. Если она имеется, то и без подробного исследо­

вания можно сказать, что работа всей схемы окажется неустойчивой, и такую обратную связь в схеме надо устранить.

ф₂ =ч>1 л:₀ /(1 + pi,).

Подставим (р₂ ^в выражение = /₂ и после небольших выкладок по­лучим характеристическое уравнение относительно приращения Дфр

Я| С_п т₁

Положение равновесия рассматриваемого звена схемы неустойчиво, так как один корень из двух корней уравнения положителен. Возникшее приращение Дф, будет нарастать до насыщения ОУ. Элемент схемы Z(p) при малом выходном сопротивлении ОУ практически не влияет на ус­тойчивость этого звена.

После проверки схемы на наличие обратной связи на положительный вход ОУ и устранения ее, если она имеется, можно приступить к иссле­дованию устойчивости работы всей схемы, В случае многоконтурной обратной связи в схеме следует учитывать:

1) что управляющие напряжения или токи управляемых источников зависят от структуры схемы, комплексной частоты р и числовых значе­ний элементов схемы;

2) что управляющая способность самих источников тока или напря­жения зависит от р (например, для операционного усилителя и транзис­

тора К-~~— или К-~---------------------- ту------------------------------------------------- ;)•

1 + J7T (1 + рт₁)(1 + /?т₂)

Порядок исследования:

1. Составляем схему замещения исследуемой цепи, указываем на ней внутренние сопротивления неуправляемых и управляемых источников и токи и напряжения, которыми они управляются. Учитываем выходные сопротивления управляемых источников.

2. Составляем выражения для управляющих токов и напряжений в функции потенциалов незаземленных узлов, параметров схемы и часто­ты р.

3. Учитываем зависимость К = f{p).

4. Составляем систему уравнений по методу узловых потенциалов подобно тому, как это было в § 15.33 (но j со заменено на р).

5. Составляем главный определитель системы и приравниваем его нулю.

Об устойчивости судим по характеру корней. Степень характеристи­ческого уравнения определяется числом энергоемких элементов, незави­симо накапливающих энергию, с учетом полюсов у каждого из имеющих­ся в схеме частотно-зависимых управляемых источников. Перечисленные условия минимальны.

В заключение обратим внимание на то, что исследование устойчиво­сти периодических режимов в нелинейных цепях на частоте вынуждаю­щей силы может быть проведено не только путем придания приращений Ап и Д£> амплитудам а и b синусной и косинусной компонент периодичес­кого режима, но и другим путем, путем исследования устойчивости пе­риодического режима к малым скачкообразным возмущениям какой либо определяющей работу схемы величине, например потокосцепления нелинейной индуктивности или заряда нелинейного конденсатора q.

Естественно, что в этом случае все выкладки должны быть проведе­ны по отношению к малому возмущению Ац/ или, соответственно, А?. Такой путь исследования устойчивости периодических режимов являет­ся в ряде случаев предпочтительным, так как позволяет учесть влияние четных гармоник на устойчивость. Применительно к линейным цепям с периодически изменяющимися параметрами он рассмотрен в § 18.6, а к исследованию устойчивости периодических режимов в нелинейных це­пях — в § 18.7. Вопросы устойчивости странных аттракторов различных типов в цепях с резистивным, индуктивным и емкостным нелинейными элементами рассмотрены в Приложении П10 и в § 15.72.

Вопросы для самопроверки

1. Дайте определение системы, устойчивой «в малом», «в большом» и устойчивой по Ляпунову. 2. Изложите общие основы исследования устойчивости «в малом». 3. При вы­полнении каких условий можно ожидать неустойчивого режима работы электрической цепи на постоянном токе? 4. Может ли быть неустойчивым режим вынужденных колебаний? режим автоколебаний? 5. Сформулируйте критерий Гурвица. 6. Как по коэффициентам

характеристического уравнения, составленного для малых приращений, можно судить об устойчивости системы? 7. В каких группах электрических цепей можно ожидать неустой­чивых режимов работы? 8. Изобразите схемы замещения HP с S- и ^/-образной ВАХ для

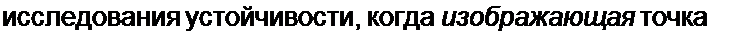Покажите, что для этих схем выполняются условия

Re Z(j < 0 и Re Z(j (о)^^ > 0. 9. Какие фи-

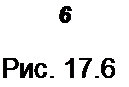зические процессы в нелинейных резисторах могут учитывать L_n и R_ao$ в схеме замещения на рис. 17.2, а и С„ и R_ao6 в схеме замещения на рис, 17.2, в? 10. Для режима автоколебаний в схеме на рис. 17.3, б постройте одну под другой зависимо­сти u_e, i_c, iff, i в функции времени /. 11. Восполь­зовавшись выкладками, приведенными в § 17.5, определите минимальные значения емкости конден­сатора С в схеме на рис. 17.3, б, меньше которого по­ложение равновесия устойчиво, несмотря на то что точка равновесия (точка m на рнс. 17.3, в) находит­ся на падающем участке ВАХ HP. 12. Покажите, что состояние равновесия в схеме на рис. 17.3, 6, соот­ветствующее точке 2 на рис. 17.3, д, при определен­ном условии неустойчиво, а соответствующее точкам / и 3 — устойчиво. 13. Изложите идею исследования устойчивости вынужденных колебаний и автоколеба­ний. 14. Сформулируйте алгоритм исследования устойчивости работы электрической цепи, содержа­щей управляемые источники напряжения или тока.

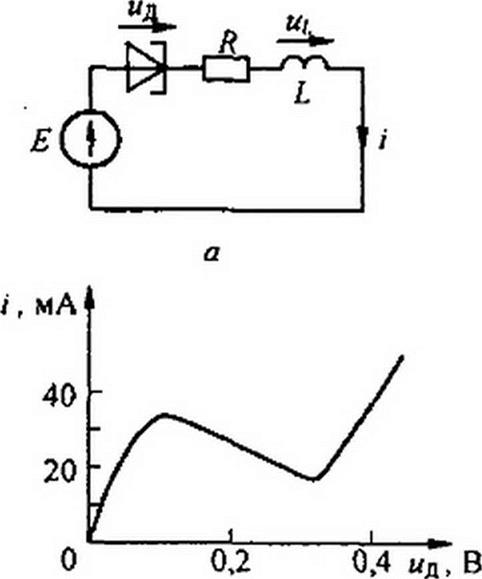
15. На рис. 17.6, а изображена схема генератора на туннельном диоде. ВАХ диода дана на рис. 17.6, б: Е = 0,3 В, R = 5 Ом. Построить кри­вые /, ц_д, u_L в функции времени при автоколебаниях. Вывести формулу для значения Д, начиная с которого возникнут автоколебания, воспользовавшись схемой замещения (см. рис. 17.2, в). (Ответ: L > |С_П(/?-R'^^R^ - •)

Глава восемнадцатая

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ