Следствием теоремы Гурвица является лемма: все коэффициенты характеристического уравнения (а0, ah а2,а„) устойчивой системы пол ожит елъны.

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Из изложенного вытекает, что для системы с характеристическим уравнением второго порядка положительные вещественные корни (или комплексно-сопряженные с положительной действительной частью) име­ют место в том случае, если какой-либо из коэффициентов уравнения (<7₀, а₃) окажется отрицательным. Для системы с характеристическим

уравнением третьего порядка положительные вещественные корни (ком­плексно-сопряженные с положительной действительной частью) будут в том случае, если:

а) какой-либо из коэффициентов (t?₀, a_[ta₂, а₃) окажется отрицатель­ным;

б) а_} а₂ ~a_Q а₃ < 0.

Аналогичные заключения могут быть сделаны и для систем с харак­теристическими уравнениями более высоких порядков.

Коэффициенты а₀,а_1уа₂^.. могут оказаться отрицательными в сле­дующих основных случаях:

§ 1.1 да в состав исследуемой на устойчивость системы входят нели­нейные резисторы (HP), обладающие падающим участком характерис­тики, а точка равновесия оказывается на падающем участке характе­ристики;

§ 1.2 схемах с чрезмерно большим воздействием выходной величины на входную (в схемах с чрезмерно большой положительной обратной связью). В этом случае поступление энергии из выходной цепи во вход­ную превышает потребление энергии во входной цепи и приращение /\х возрастает;

§ 1.3 схемах с управляемыми нелинейными индуктивностями (нелиней­ными конденсаторами) при наличии неявно (в некоторых случаях и явно) действующих обратных связей. В таких схемах обратные связи при оп­ределенных условиях приводят к появлению на характеристиках нелиней­ных индуктивностей (нелинейных конденсаторов) падающих участков. Режим работы системы может быть неустойчивым, если изображающая точка окажется на падающем участке характеристики управляемой нели­нейной индуктивности (нелинейного конденсатора).

§ 1.4 Исследование устойчивости состояния равновесия в сис­темах с постоянной вынуждающей силой. Когда рабочая точка по постоянному току окажется на падающем участке ВАХ, то состояние равновесия в системе при определенных условиях может быть неустой­чивым. В этом случае при исследовании устойчивости нелинейный резистор заменяют расчетной схемой — схемой замещения. Она должна учитывать свойства HP как при медленных (при со -> 0), так и при быст­рых (при со —> оо) малых приращениях тока и напряжения на HP.

Свойства HP при со -> 0 определяются самой ВАХ HP, снятой при постоянном токе, на падающем участке которой дифференциальное со­противление /?_диф < 0.

Если к HP подвести некоторое постоянное напряжение или через него пропустить некоторый постоянный ток такого значения, чтобы рабочая точка находилась на падающем участке ВАХ, и затем воздействовать на
HP синусоидальным напряжением или током малой амплитуды, то сопро­тивление Z(j со), оказываемое HP синусоидальной составляющей малой амплитуды, будет представлять собой комплексное число. Опыт показы­вает, что при достаточно большой о действительная часть этого сопро­тивления оказывается положительной, т. е. ReZ(jto)>0. Объясняется это тем, что физические процессы в самом HP инерционны, причем инер­ционность (сдвиг по фазе между синусоидами напряжения и тока) силь­нее проявляется с ростом частоты.

В одних HP инерционность вызвана тепловыми процессами, в дру­гих — процессами накопления энергии в электрическом и (или) магнит­ном полях, в третьих — процессами ионизации и деионизации (которые также протекают не мгновенно), в четвертых — инерционностью про­цессов диффузии носителей тока и емкостью, обусловленной объемны­ми зарядами. Но чаще всего инерционность есть следствие нескольких взаимно связанных друг с другом процессов.

Таким образом, схема замещения HP, когда точка равновесия находит­ся на падающем участке характеристики, по отношению к малым при­ращениям должна быть такой, чтобы при <о -> 0 Re Z(j со) - Я_диф < 0, а присос оо ReZ(jco)>0.

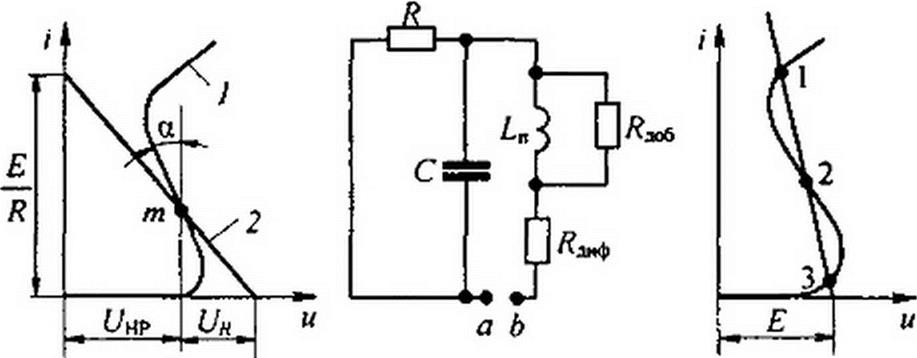
На рис. 17.2, а изображена одна из возможных схем замещения для HP с S-образной ВАХ (рис. 17.2,6), удовлетворяющая перечисленным условиям. В этой схеме L_n — некоторая малая индуктивность, которую часто называют «паразитной», /?_доб > | Я_диф | > 0 — некоторое добавочное активное сопротивление.

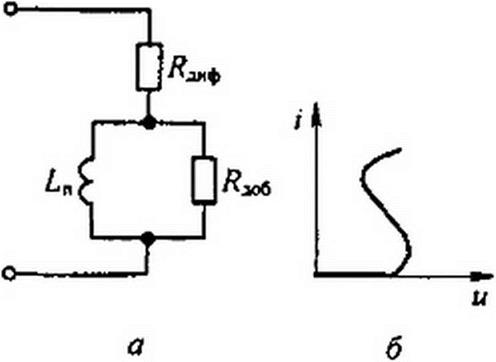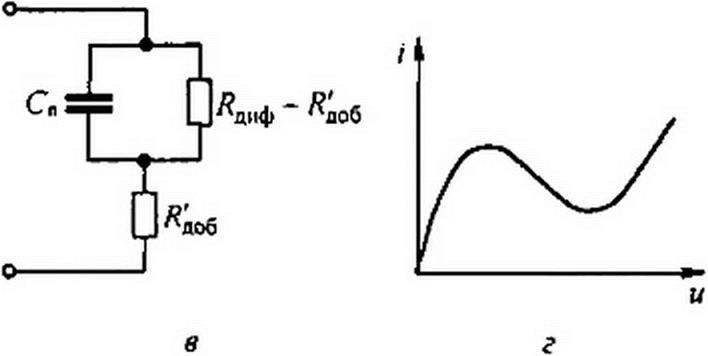
На рис. 17.2, в изображена одна из возможных схем замещения для HP с //-образной ВАХ (рис. 17.2, г), где С_п— некоторая малая емкость, называемая часто «паразитной», и /?_доб >0— некоторое добавочное ак­тивное сопротивление. Параметры L_n и /?_доб, а также С_п и /?_доб зави­сят от физических процессов в HP и изменяются при переходе из одной точки на падающем участке ВАХ в другую.

§ 1.5 Исследование устойчивости автоколебаний и вынужден­ных колебаний по первой гармонике. Исходными при исследовании устойчивости автоколебаний и вынужденных колебаний обычно являются уравнения, получаемые по методу медленно меняющихся амплитуд

(§ 16.6). Однако в тех случаях, когда напряжение на каком-либо элемен­те (ток в исследуемой цепи) резко отличается по форме от синусоиды, например имеет пикообразную форму, исследование устойчивости целе­сообразно проводить по средним за полпериода значениям величии.

Если через а и b обозначить медленно меняющиеся амплитуды синус­ной и косинусной составляющих исследуемого колебания, то из исход­ных уравнений системы можно получить два уравнения для медленно меняющихся амплитуд:

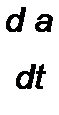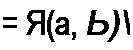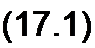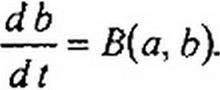
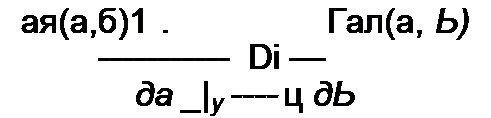(17.2)

Здесь А и В являются функциями амплитуд а и Ь, функциями пара­метров схемы, угловой частоты колебаний со и амплитуды вынуждаю­щей силы. Обозначим значения а и b в установившемся режиме (когда амплитуды не изменяются во времени) через a_Q и Л_о. Для определения а₀ и Ь_о в (17.1) и (17.2) следует положить da/dt-Q и db/dt = Q и решить систему уравнений:

Л(а_о,6_о) = О;

£(a_o,Z>_o) = O.

Пусть в результате возмущения амплитуды колебания получили ма­лые приращения Да и &Ь и стали равными: а = а₀+Да и 6 = 6_О+Д6.

Подставим эти значения а и b в (17.1) и (17.2), разложим A(a_Q + Да, b_Q + Д6) и В(а₀ + Да, b_Q + Д6) в ряд Тейлора по малым при­ращениям Да и Д6, в силу малости приращений ограничимся слагае­мыми ряда с первыми степенями Да и Дб. В результате получим:

А(а₀ + &a,b_Q + Д6) = Л(а₀,6₀) + Да +Д6

В(а$ + Да, 6₀ + Дд) - B(a_Q, b_Q) + Да А₂ + &Ь В₂.

Для сокращения записи обозначено;

Индекс «у» свидетельствует о том, что в частные производные долж­ны быть подставлены значения а и b установившегося режима, т. е. а₀ и Ьц.

Коэффициенты А_[УВ_[}А₂,В₂ являются функциями а₀ и Ь_Оу ноне являются функциями приращений Да и Дб. Подставим правые части (17.5) и (17.6) в (17.1) и (17.2), учтя при этом (17.3) и (17.4), а также то, что

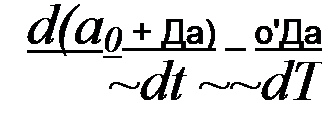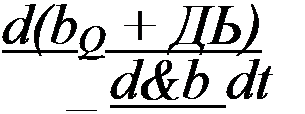В результате получим два уравнения:

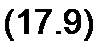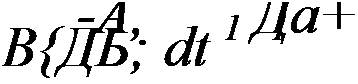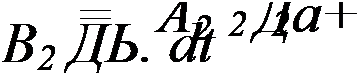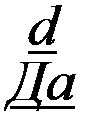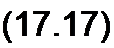Алгебраизируем их:

р Да « А_} Дач- В_} ДА;

р ДЬ = А₂ Да+ В₂ ДЬ.

Составим характеристическое уравнение р² + т p + q = О, где

^т = ~(Л[ ч- А₂У,
q = А_{ В₂ - В| А₂.

В соответствии с критерием Гурвица для затухания приращений Да и ДЬ необходимо, чтобы

т > 0, q > 0.

В автоколебательных системах периодические вынуждающие силы, как правило, отсутствуют, поэтому можно принять Ь - 0, т. е. взять ко­лебания в виде a(f)sinci)/ (см. пример 164). В этом случае вместо двух уравнений — (17.9) и (17.10) — будет одно уравнение

где

(17.18)

Для устойчивости автоколебаний в этом случае необходимо выполне­ние условия А₁ <0.

Пример на исследование устойчивости автоколебаний по формуле (17.15) см. в § 17.6.

§ 1.6 Исследование устойчивости состояния равновесия в генераторе релакса­ционных колебаний. Релаксационные колебания представляют собой автоколебания, при определенных условиях возникающие в нелинейных электрических целях с одним нако­пителем энергии, например в цепи с одним конденсатором (без индуктивного элемента) или с одним индуктивным элементом (без конденсатора).

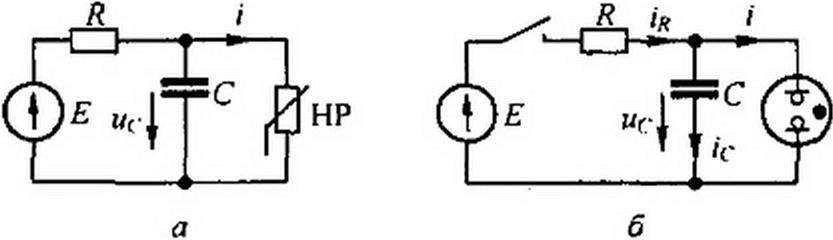
На рис. 17.3, а изображена принципиальная схема генератора релаксационных коле­баний. Она состоит из источника постоянной ЭДС £, линейного резистора сопротивлени­ем R, конденсатора емкостью С и параллельно соединенного с ним нелинейного резисто­ра, имеющего ВАХ S-образной формы.

£

Рис. 17.3

В качестве HP с такой ВАХ могут быть взяты неоновая лампа или тиратрон. На рис. 17.3, б дана схема генератора с неоновой лампой. Кривая 1 (рис. 17.3, в) представ­ляет собой ВАХ неоновой лампы, прямая 2 — ВАХ R.

Если бы не было релаксационных колебаний, то режим работы определился бы точ­кой т пересечения кривой / и прямой 2. Для этой точки сумма падений напряжений на HP и Л, в соответствии со вторым законом Кирхгофа, равна ЭДС £: ¹ R^{+ W}Kp = £.