Если ОТ окружена свертывающейся спиралью, то ее называют устойчивым фокусом (рис. 16.12, е); ей соответствуют комплексно-сопряженные корни с отрицательной действительной частью.
Если ОТ окружена раскручивающейся спиралью, то ее называют неустойчивым фокусом (рис. 16.12, ж\, ей соответствуют комплексно-сопряженные корки с положительной действительной частью.
Если корни отрицательные и действительные, то ОТ называют устойчивым узлом (рис. 16.12, з). При положительных действительных корнях получают ОТ типа неустойчивого узла (рис. 16.12, и). Когда один корень положителен, а другой отрицателен, имеем ОТ типа седло (рис. 16.12, к).
Рассмотрим переходный процесс в схеме на рис. 16.13, а, вызываемый замыканием ключа при нулевых начальных условиях: Е = 1 В; R = 1 Ом; L = 1 Гн; С -1Ф.
 |
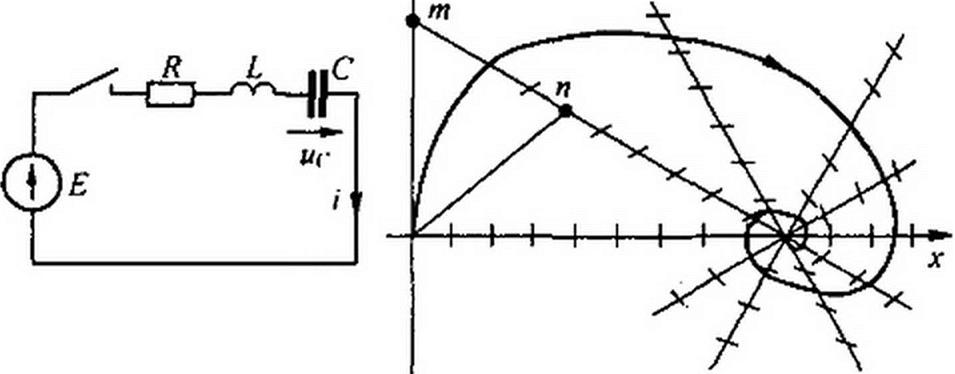а б
Рис. 16.13
Построим семейство изоклин для напряжения на конденсаторе и^. Определим положение и тип ОТ. Построим фазовую траекторию переходного процесса.
В уравнении цепи
£С — f^l + flC^- + uc = Е
dt\ dt ) di (
d dу dx dу , „ Л „
заменим u<- нах, —на.у, —у на ———— -у — — и учтем, что L- R = С = E = 1.
d{ dt dx dt dx
d у
Решим уравнение y— + y + x = i относительно у и dy/dx'.
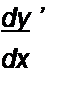(16.96)
(16.97)
Из уравнения (16.97) следует, что координаты особой точки у = 0, х = 1. Последовательно придавая dyjdx значения 0,1,2, ...,-1,-2, <®, строим семейство изоклин (рис. 16.13. б). Все изоклины проходят через ОТ и представляют собой прямые линии (цепь линейна). Масштабы по осям хну приняты одинаковыми. Черточки на каждой изоклине характеризуют значение dy/dx для нее.
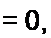
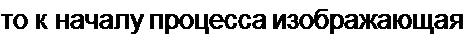Так как х(0) = и с (0) = 0 и у’(0) ~ ~ точка находится в начале координат. В установившемся режиме х » 1 и у = 0.
Для построения интегральной кривой из исходной точки х = у = 0 проводим два луча до пересечения с изоклиной dу /dx = 1 в точках т и п. Первый луч соответствует значению dy/dx-az той изоклины, с которой начинается движение, второй — значению
= 1 следующей изоклины, на которую точка перейдет. Делим расстояние тп пополам dx
и проводим через исходную и полученную точки плавную кривую — кусочек фазовой траектории. Продолжаем аналитический процесс далее и строим всю фазовую траекторию в виде свертывающейся спирали.
ОТ в примере является устойчивым фокусом. Время в явном виде на фазовой плоскости не отражено.
d х
Временные зависимости х- f(t) по фазовой траектории у =— = ср(х) получают по d t
формуле
г
1 j <₽М ’
. . . . хо где xq — начальное значение, ах — текущее. В окрестности точки пересечения кривой с осью абсцисс подынтегральное выражение стремится к бесконечности. Чтобы избежать планиметрирования площади под кривой, уходящей в бесконечность при ф(х)->0, подсчет времени Дг на этом участке производят по средней скорости <рср(х) = Дх/фср(х).
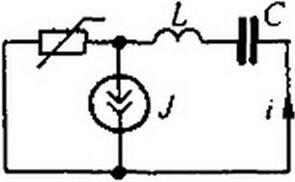
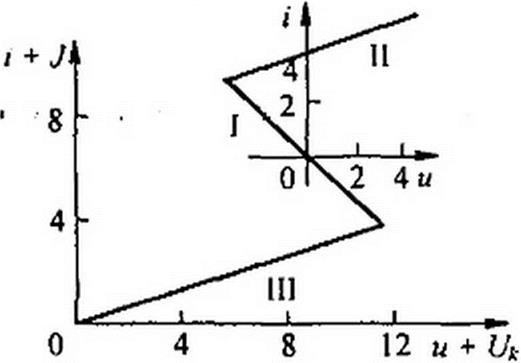
Пример 166. Рассмотрим колебательный процесс в схеме на рис. 16.14, а. В этой схеме Д = 1Гн; С = 1/ЗФ, ВАХ нелинейного резистора i + j = f(u + UK) изображена на рис. 16.14, б. Ток источника постоянного тока J = IА . ВАХ относительно переменных составляющих тока г и напряжения и на резисторе получена переносом начала координат в точку J = 7 А . Эта ВАХ состоит из трех участков. На участке I и = -i (| * | - 3), на участке II и = 3,-12 (/>3), на участке 111 u = 3i + 12 (/>3).
 |
|
 |
|
 |
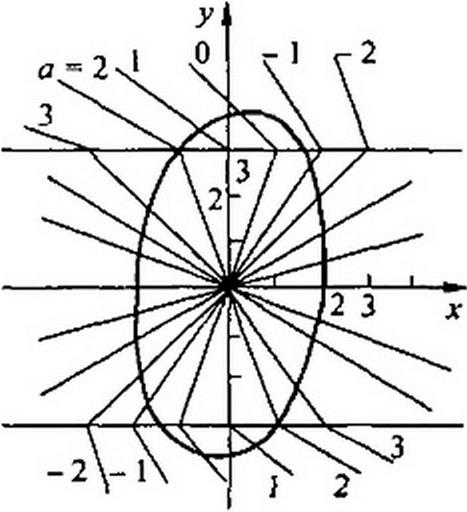Рис. 16.14
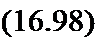Обозначим переменную составляющую заряда конденсатора q ~ х. Учтем, что сумма падений напряжений для переменных составляющих
“я + »L + «с - «я +1-77
a I
ток
dq did dy dx dy
i - — - у; — = — у = —---------------------------- = a у ; a ~ .
dl dt dt dx dt dx
Подставим соответствующие эквиваленты в (16.98) и запишем уравнение изоклин на каждом из участков:
1 3 х
на участке I у ------------- ,
1 -а
.. 12 3 х
на участке II у ------------------------ ,
3+а 3 + а
12 3 х
на участке III у =------------------------- .
3 + а 3+а
В соответствии с этими уравнениями строим на рис. 16.14, в семейство изоклин для каждого из участков. Изоклины являются отрезками прямых. Значения а написаны рядом с соответствующей изоклиной. Жирной линией показан предельный цикл.
В заключение обратим внимание на то, что в большинстве рассмотренных методов расчета переходных процессов в нелинейных цепях характеристика нелинейного элемента принималась не зависящей от скорости процесса, гистерезисных и других подобных явлений. В тех случаях, когда учет этих явлений необходим, единственная характеристика нелинейного элемента должна быть заменена семейством кривых, учитывающим перечисленные факторы. Для решения задач на переходные процессы с учетом этих факторов может оказаться полезным графоаналитический метод В. Волынкина, предложенный им еще в 1916 г. и рассмотренный нм на примере цепи: нелинейная индуктивность, линейный резистор и ЭДС. Этот .метод использует графическое описание характеристики нелинейного элемента, подсчет определенного интеграла по формуле трапеций и простые графические построения. Идея метода и дальнейшее его развитие в цепях второго и третьего порядка при наличии в них разнородных нелинейных элементов даны в § 16.3 (но пока с однозначными характеристиками нелинейных элементов). Наличие у каждого или у части нелинейных элементов целого семейства характеристик может быть учтено методом последовательных приближений.
Вопросы для самопроверки
1. Охарактеризуйте известные вам группы методов расчета переходных процессов в нелинейных цепях. 2. Укажите, в чем положительные и 8 чем отрицательные стороны расчетов по мгновенным значениям и по огибающим первых гармоник, графоаналитических и аналитических методов. 3. Почему метод расчета, основанный на графическом подсчете определенного интеграла, неприменим даже для цепей первого порядка, если вынуждающая сила является функцией времени? 4. Почему метол интегрируемой нелинейной аппроксимации не удается применить к электрическим цепям, описываемым уравнениями второго и более высоких порядков? 5. Чем физически можно объяснить, что при подключении линейной ЯЛ-цспи к источнику синусоидальной ЭДС максимальное значение тока при переходном процессе не может превысить удвоенного значения амплитуды тока установившегося режима, тогда как при подключении цепи резистор—индуктивность с нелинейной ВАХ к источнику синусоидальной ЭДС это превышение может быть во много раз больше? 6. Сформулируйте особенности расчета переходных процессов в нелинейных системах не чисто электрических, например электромеханических. 7. На примере цепи с термистором покажите, что бывает полезно подразделить переходный процесс на быстро и на медленно протекающие стадии и рассматривать их раздельно. 8. В чем идея метода малого параметра? 9. Запишите и прокомментируйте рекуррентное соотношение, явля
ющееся решением нелинейного интегрального уравнения. 10. Охарактеризуйте идею метода медленно изменяющихся амплитуд. 11. Как расчетным путем учитывают магнитную вязкость при перемагничивании ферритовых сердечников импульсами тока? 12. Дайте определение фазовой плоскости, интегральной кривой, фазовой траектории, предельного цикла, изоклины, особой точки. 13. По какому признаку классифицируют особые точки? 14. Как по фазовой траектории у = /(х) построить временную зависимость х(/)?
Глава семнадцатая