Интегральную кривую, проходящую через точку ФП с заданными начальными условиями, называют фазовой траекторией.
Вид фазовой траектории зависит от конфигурации схемы, характера нелинейности и соотношения между параметрами.
Если процесс в цепи является периодическим, то через интервалы времени, равные периоду процесса, соответствующие друг другу значения х и у повторяются, и фазовая траектория в этом случае является замкнутой кривой. Замкнутую фазовую траекторию называют предельным циклом.
Если интегральные кривые и снаружи и изнутри навиваются на предельный цикл, то его называют устойчивым, если удаляются от него — неустойчивым. Если же процесс непериодический, то фазовая траектория представляет собой незамкнутую кривую.
Фазовую траекторию можно наблюдать на экране электронно-лучевого осциллографа С этой целью на одну пару отклоняющихся пластин его подают исследуемую величину х, а на другую пару — производную от х.
§ 2.18 . Изображение простейших процессов на фазовой плоскости. Рассмотрим несколько простейших примеров.
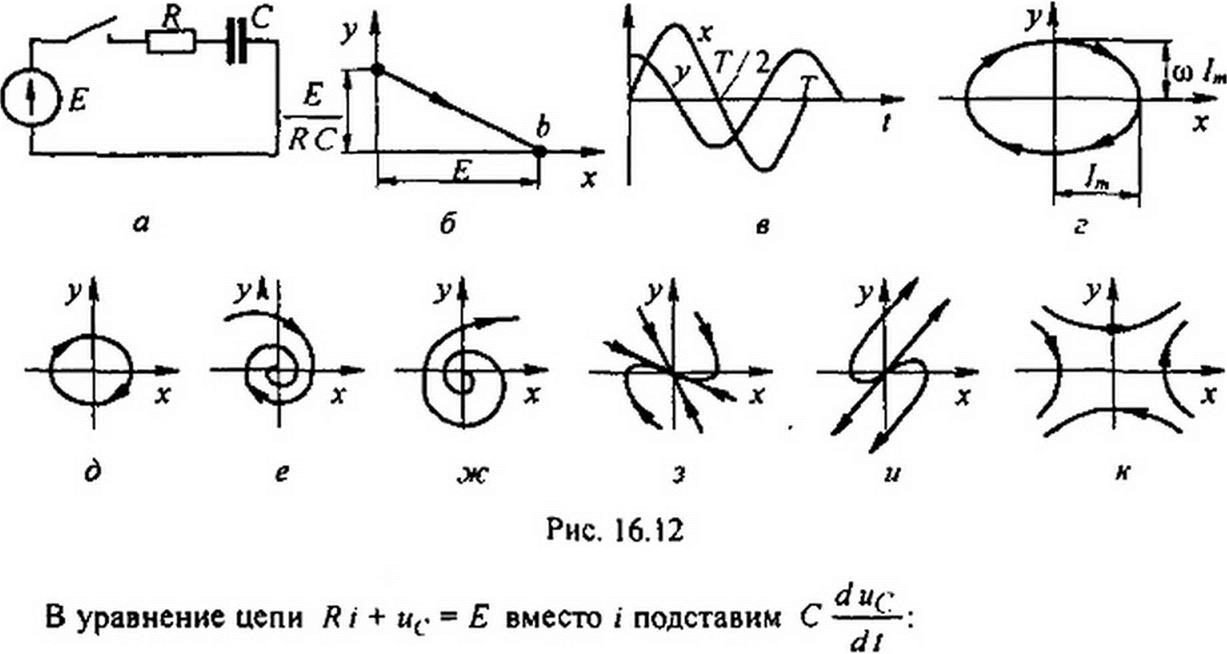
Требуется изобразить на ФП переходный процесс в схеме на рис. 16.12, а, вызываемый при нулевых начальных условиях замыканием ключа. Обозначим: / — ток в цели, ис — напряжение на конденсаторе.
 |
|
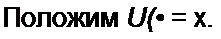 | 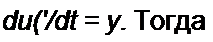 | ||
Последнее уравнение описывает прямую а b (рис. 16.12, б), которая является фазовой траекторией рассматриваемого процесса (точка Ь — точка равновесия).
Рассмотрим изображение на ФП синусоидального колебания i = /msin<i)t (рис. 16.12, а).
Обозначим / = х , тогда
d х ,
у = —— = СП lm COSO /,
d i
x«/OTsino/; у = cd lm cosco t.
Разделив первое уравнение на 1т, второе — на <o/w, возведя 8 квадрат полученные выражения и сложив их. получим уравнение эллипса
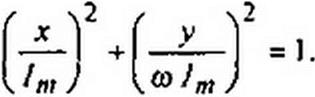 |
Следовательно, изображением синусоидального процесса (фазовой траектории) на ФП является эллипс (рис. 16.12, г).
Направление движения изображающей точки показано стрелкой. В верхней полу- , dx
плоскости у = — > 0, следовательно, изображающая 'точка движется в сторону увеличе- dt
ния
координаты х. В нижней полуплоскости ~ < 0, поэтому изображающая точка движется dt
в сторону уменьшения координаты х. В целом перемещение изображающей точки на ФП происходит всегда по часовой стрелке.
§ 2.19 . Изоклины. Особые точки. Построение фазовых траекторий. Тангенс угла наклона, образованного касательной к интегральной кривой в некоторой точке ФП и осью абсцисс, определяет значение dyfdx в этой точке. Совокупность точек ФП, для которых
dy/dx = const, называют изоклиной. На ФП можно провести множество изоклин, каждой из которых соответствует свое значение d у (dx.
Для всех точек ФП, отражающей процессы в цепи второго порядка (кроме особых точек), dy/d х имеет вполне определенное значение. В особых точках (ОТ) dyjdx- 0/0, т. е. не определено. Через эти точки может быть проведено множество изоклин с различными значениями dy/dx.
ОТ классифицируют по виду интегральных кривых, окружающих эти точки.
Если ОТ окружена эллипсами (рис. 16.12. д), то ее называют ОТ типа центр-, она соответствует двум мнимым корням характеристического уравнения.








