« —•) и оставим слагаемые первого порядка dt

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

малости. В результате получим

d²x С 2 db\ . ( 2 l da\

—г-«- со а + 2со— sin(o/+ -со о+ 2со— cosco/.

dt² I dt) I dt)

Обратим внимание на то, что слагаемые первого порядка малости ос­тавлены в выражении для d²x! dt² и их не учитывают в выражении для dxl dt. Объясняется это тем, что исследуемая цепь обладает малыми потерями, поэтому амплитуда второго слагаемого левой части (16.14) от­носительно мала по сравнению с амплитудами первого и третьего слага­емых левой части (16,14).

В функцию f(x) вместо х подставим (16.15) и разложим /(х) вряд Фурье. Затем умножим ряд Фурье, которым выразилось /(х), на dxldt (на правую часть (16.18)). Таким образом,

dx

f(x) — = F(da,b) + Fi(a,Z))sin<o/ + S(cz,6) cosco / + dt (16.20) + F₃(a,6) sin 2 co l + F₄(a,b)cos2 co / + ....

Так как расчет ведется по первой гармонике, то постоянной состав­ляющей F₀(a, b) и высшими гармониками ряда Фурье (F₃(a, b), F_A(a, Ь) и др.) в дальнейшем пренебрегаем.

В (16.14) подставим правую часть (16.19) вместо d²x/dt\ F_} (a, b) sin со / + F₂( а,Ь) cosco t вместо f\x}dxldt и coq {a sin со / + +bcosco/) вместо сод х.

Тогда (16.14) можно разбить на два уравнения. Одно из них (уравне­ние (16.21)) будет выражать собой равенство коэффициентов при cosco/ в левой и правой частях (16.14), другое (уравнение (16.22)) — равенство
коэффициентов при sin <о t в левой и правой частях (16.14):

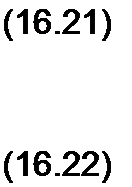-2© — + F_](a_>b) + a (cOq - со²) 4; dt

2о)^+Г₂(а,6) + 6(а)^-со²) = О. dt

Система уравнений (16.21) и (16.22) представляет собой два совмес­тных дифференциальных уравнения, составленных относительно мгно­венных значений медленно меняющихся амплитуд а и Ь.

В общем случае решение этой системы может проводиться методом малого параметра или методами численного интегрирования. В частном случае, когда внешняя периодическая сила равна нулю (Л = 0) и функ­ция = 0, система сводится к одному дифференциальному урав­нению первого порядка

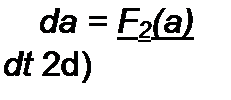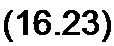Ранее были рассмотрены основные этапы перехода от дифференци­ального уравнения для мгновенных значений (уравнение (16.14)) к диф­ференциальным уравнениям для медленно меняющихся амплитуд. Метод применим и к уравнениям более высоких порядков.

В заключение необходимо отметить, что если максимальное значение слагаемого f(x)dx!dt в (16.14) (и подобных ему), выражающее собой падение напряжения в активном сопротивлении контура (контуров), соизмеримо с максимальными значениями остальных слагаемых (16.14), то в выражении dx/dt должны быть сохранены слагаемые первого порядка малости, которыми ранее пренебрегли. Огибающая колебаний определяется уравнением

/СО = 4a\t) + b\t).

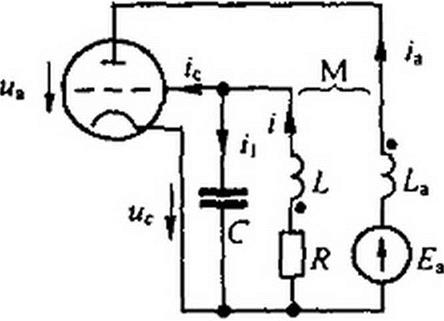
Пример 164. Определить закон нарастания амплитуды напряжения на сетке в лампо­вом автогенераторе (рис. 16.5).

Решение. В соответствии с обозначениями на рис. 16.5 составим уравнение по вто­рому закону Кирхгофа для сеточной цепи:

L — М — — + R i + Uf ® 0. (16.24)

dt dt

d U/'

Подставим в него i = C——. Получим dt

dr dt dt

Анодный ток i_a выразим через напряжение сет­ки (см. (15.39»: /_а = r_a0 + а' и_с - b и}-.

Ho = (д'— 3b и)- ) . Подставим — в (16.24):

dt dt dt

^-^RC-a' M + 3bM + =0.

dt² ' dt ⁽

Поделим последнее уравнение на LC = l/w©. где co_o — угловая частота автоколеба­ний, и обозначим

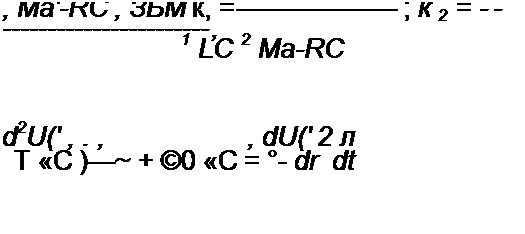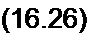Примем

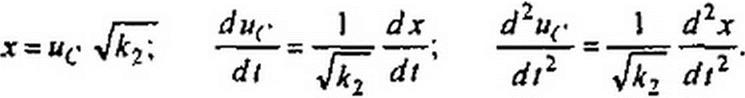Тогда

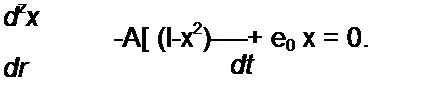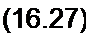Множитель -^(1-x²) и представляет собой функцию f{x) уравнения (16.14). Так как на систему не действует внешняя периодическая сила и частота автоколебаний равна со_о, а не <о, то примем

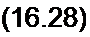dx

х = a sin ю₀ ц — cos о₀ Г,
dt

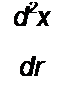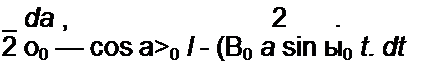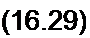Подставим (16.28) и (16.29) в (16.27) и учтем, что

sin² w₀ t cos w₀ i = 0,25 (cosa₀ / - cos3 o₀ t) - 0;

da > • 2 ।

2 cosojq t------------ a e₀ sino₀ t + a <a₀ sm£o₀ t- k, a g>₀ coso>₀ f +

dt

+ 0,25 A, a³ (coso)₀ t - cos 3 co_o t) ~ 0.

Так как расчет ведем по медленно изменяющейся по амплитуде первой гармонике, то слагаемое с cos3 w₀ t ие учитываем. Следовательно,

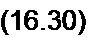2 — ^ак, (1-0,25<?)-
dt

Введя новую переменную у = 0,25 a². получим

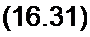~ У 0 - Л

at

Уравнение (16,31} — это уравнение с разделяющимися переменными

,y^V S M = -*nCo+ln~->

^Jy(l~y) 1-у

где 1пС₀ —постоянная интегрирования:

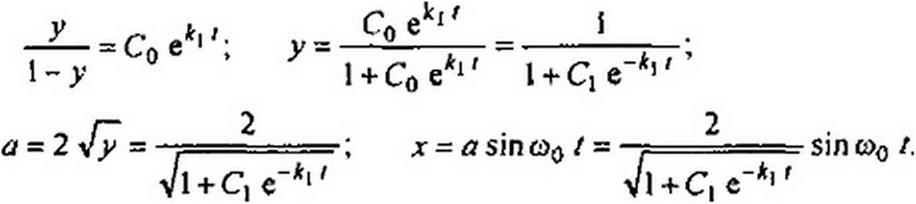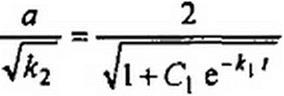
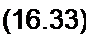
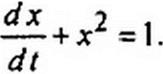
(16.32)

Постоянную интегрирования С₍ определим по начальному значению. Если при / = 0 ^•=^с(0_),то

С ⁴ a'M-RC _{

¹ ^(0.) ^зьм

Мгновенное значение напряжения на конденсаторе

и_е = Uс sin <о_о I.

§ 16.8. Метод малого параметра. Нелинейные дифференциальные уравнения иногда решают путем последовательных приближений, пред­ставляя искомую величину х в виде ряда по степеням некоторого коэф­фициента ц, который называют малым параметром:

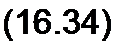X = Xq +pxj +ц² х₂ + ...,

где л₀— решение уравнения нулевого приближения (последнее получают из исходного, полагая, что все нелинейные члены в исходном уравнении отсутствуют); — решение уравнения первой поправки, которая учиты­вает влияние нелинейных членов в первом приближении; х₂ — решение уравнения второй поправки и т. д.

Если исходное уравнение является дифференциальным уравнением второго или более высокого порядка, а принужденный режим представ­ляет собой колебательный процесс, то квадрат угловой частоты первой гармоники со² или первую степень со также разлагают в ряд по малому параметру:

со² =соо +h/i +Ц²/г’

где со²— квадрат угловой частоты в нулевом приближении, когда всеми нелинейными членами пренебрегают; р. / — поправка первого прибли­жения, вызванная нелинейными членами уравнения; р² f₂ — поправка второго приближения, и т. п.

Последовательность решения рассмотрим на двух примерах.

1. При х(0) = 0 решить уравнение

(16.35)

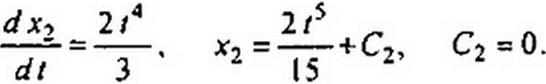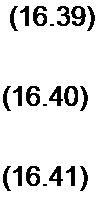
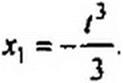
К такому уравнению, например, сводится задача о переходном процессе в цепи, со­стоящей из нелинейной индуктивности с нелинейной ВАХ и линейного резистивного со­противления. при подключении ее к источнику постоянного напряжения и при квадратич­ной аппроксимации зависимости потокосцепления от тока.

Линейные члены уравнения переносим в левую часть, а нелинейные, умножив на не­который малый параметр р,в правую (в примере р = 1).'

—-! = -цх². (16 36)

dt

Представим решение (1635) в виде ряда по степеням М :

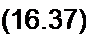x = x₀+px₁+j? х₂+....

Подставим (16.37) в (16.36):

~?’ ⁺ М~’ ⁺ М² ₌ -р² 2 х₀ X) -р’ (х² +2х₀ х₂). (16.38)

dt at al

Из (16.38) образуем систему уравнений, приравняв члены левой и правой частей его при одинаковых степенях р :

с/х₀ , „

—----- 1 = о — уравнение нулевого приближения;

dt

t/x, ₂

— уравнение для первой поправки;

d Xj

—— - -2 х₀ Х| — уравнение для второй поправки. d I

Проинтегрируем (16.39): х₀ =t + C₀.

Постоянную С_о = 0 определили из начальных условий.

Подставим х₀ = / в уравнение (16.40) и проинтегрируем его:

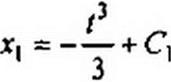
Для первой поправки начальные условия также нулевые, поэтому С, = 0; Подставим значения х₀ и х₍ в (16.41):

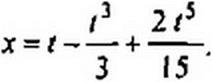В соответствии с (16.37)

(16.42)

Аналогично можно было бы получить и последующие члены ряда (16.37). Так как уравнение (16.35) имеет точное решение x = th/, то, взяв в разложении th/ три первых члена ряда, можно убедиться, что они совпадают с правой частью (16.42).

2. Решить уравнение для лампового генератора (вывод уравнения см. в примере 164) при начальных условиях х(0) = Л_о х'(0) = 0:

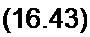d² х , .. 2х ^dx 2 л

—(I-х )-—- + g>q х = 0. dt¹ dt

Коэффициент к_х при нелинейном члене в дальнейшем будем считать малым парамет­ром и обозначим м- В соответствии с предыдущим

х = х₀ + ц Xi + ц² х₂ + ...;

, _{2 2} <^l644>

а“ = <а₀ + ц/) +р /₂+....

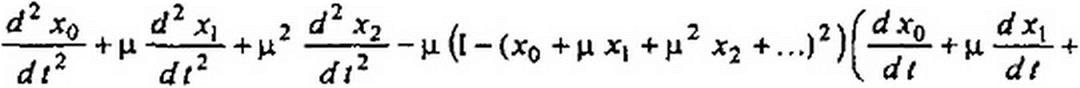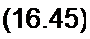В уравнении (16.43) вместо х подставим правую часть (16.44) и со² -ц / -р² /₂ вме- сто wq :

_{+ и}² ^2- ₊ ...'| ₊ (_о² -р/] __и² /₂)(х₀ +ЦД-1 +ц² х₂ + ...) = 0.
a t )

Образуем из (16.45) три уравнения, соответствующих ц в нулевой, первой и второй степенях:

j2

- ^ + ^х_о=0;---- (16.46) dt²

2

- р + о>² X, = (1-Xq)—^- + x₀/_t;--- (16.47) dr--- dl

^d ...^X2 _+(|)2 _q__x2^^j__2 _X( X) +/₂ X_O. (16.48)

dr dt dt

Проинтегрируем (16.46): x₀ - A_o cos tor.

Подставив x₀ в (16.47) и учтя, что sin a cos² а = 0,25 sin а + 0,25 sin 3 а, получим

d

■ *' + Х| = -со Л_о (1 - 0,25 Ло ) sin со / + А_о f_} cos со t +

dr (16.49)

+ 0,25<в Aq sin 3 о г.

Уравнение (16.49) можно трактовать следующим образом: на колебательный £С-кон- тур без потерь (левая часть уравнения (16.49)) воздействуют вынуждающая сила с угло­вой частотой со, равной собственной частоте колебательного контура, и сила с угловой частотой, в три раза большей.

Известно, что если подключить колебательный £С-контур, имеющий активное сопро­тивление R -> 0, к источнику синусоидальной ЭДС Е_т sin со 1 при оговоренных условиях, то амплитуда тока в цепи будет нарастать до бесконечности. Действительно,

' = 'л_Р + 'св = ~ s«nсо t - е^-5' sin(co / + v).

А А

При/?->0 v-> 0 и S =/?/(2 £)-> 0.

Разложим е"⁵' в ряд и, учитывая малость 5, возьмем два первых члена ряда. В ре- £

зультате получим i *---------- t sin со t.

Такие члены в решении дифференциальных уравнений, амплитуды которых нараста­ют теоретически до бесконечности при увеличении времени /, называют вековыми. При дальнейшем решении уравнения (16.49) необходимо помнить о том, что амплитуды веко­вых членов должны оказаться равными нулю при любом f > 0.

Решение (16.49) запишем следующим образом:

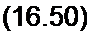X) = Л, since t + В| cosw г + (С, sin со / ч- cos to t) t +
+ Е_} sin 3 се t + 5i cos3 се /.

Первое и второе слагаемые представляют собой полное решение однородного уравне­ния; четвертое и пятое — частное решение неоднородного уравнения. Третье слагаемое представляет собой вековой член. Его можно было бы не вводить в дальнейшие выкладки по определению коэффициентов Л_р Е_и C_b D,, однако введем его, чтобы показать, что его присутствие выкладкам не помешает.

Дважды продифференцируем (16.50) по времени:

xf = -4 (a¹ sincuz-fi] со² Cosco Z +С] со cosco t- D\ cosincoz +

+ co(C| coscoz+ £>] since/)-/ co² (C| sinco/ + D_t cosco/)-9 co² £j sin3 co/ - (16.51)

-9co² F\ co$3 coz.

Подставим (16.50) и (16.51) в (16.49), выделим из левой и правой частей (16.49) сла­гаемые соответственно с sincor (формула (16.52)), cosco/ (формула (16.53)), sin3coz (формула (16.54)), cos3co/ (формула (16.55)):

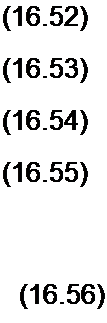= 0,5 4 (1-0,25 4²);

2 со С] - 4

-8 со² £| =0,25 со
8w² Л} =0.

Слагаемые (16.49) с вековыми членами дают нуль:

t (С] sin со / + D| cosco /) (со² - со²).

Используем также заданные начальные условия для определения , Й;, С;, , £₍, .

Так как начальные условия уже были удовлетворены при определении х₀, то для всех последующих приближений начальные условия нулевые. Имея это в виду, из (16.50) на­ходим Х](0) = fi, + = 0.

В соответствии с (16.55) F| = 0, поэтому fi_t = 0. Из уравнения (16.50). используя ус­ловие x'i = 0, получим

со Л] + £>] + 3 со £| = 0.

Но и Г) известны из (16.50) и (16.54), поэтому

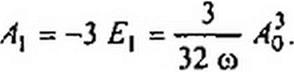Поправку на угловую частоту а вместе с тем и значение Л_(| найдем исходя из того, что амплитуда векового члена должна быть равна нулю при любом ! > 0. Отсюда С| = 0 и О| = 0.

Из (16.53) следует, что /]=0, а из (16.52) — что 4 ⁼ 2:

3

А\ - “— Ло, fi, - 0, С| = D\ = 0. Е\ — ——, Л] « 0, со = соф.

32 св 32 со

Ограничившись первым приближением и перейдя от И к Л,, получим

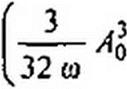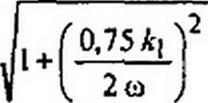Первое приближение привело к изменению амплитуды первой гармоники с 4=2 до и к появлению третьей гармоники.

Угловая частота первой гармоники в первом приближении не изменилась и равна угловой частоте со_о нулевого приближения. Аналогично производится и второе приближе­ние. Однако каждое последующее приближение по сравнению с предыдущим более тру­доемко.

В основу данного метода положены работы французского математи­ка Пуанкаре по небесной механике. Метод называют методом малого параметра, потому что в нем выполняют разложение решения в ряд по
степеням малого параметра. Насколько этот параметр должен быть мал в каждом примере, заранее сказать нельзя. Важно, чтобы ряды для х и для со² или (о сходились. Если ряды будут сходиться медленно или вообще не будут сходиться, то пользоваться этим методом не имеет смысла.

§ 16.9. Метод интегральных уравнений. От нелинейного дифферен­циального уравнения можно перейти к интегральному, используя одну из форм записи интеграла Дюамеля. Поясним идею этого перехода. Реше­ние линейного дифференциального уравнения, например уравнения

(16.57)

может быть записано в виде:

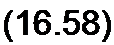х(О = ЛО g(0) + /Л^т> - т) d т.

о

Под g(r) понимают переходную проводимость либо переходную функцию, в зависимости от того, чем является х по отношению к вынуж­дающей силе/(/); g(0 определим как решение (16.57) приу(/) = 1.

Если исходное уравнение нелинейно, например:

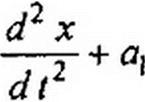то нелинейный член b х² можно перенести в правую часть и рассматри­вать как внутреннюю вынуждающую силу:

с/² X с/х _ч , 2

~d? ^{+ Q]} ~d7 ⁺ “° ^{Х =} " ^{b х} *

Используя (16.58), запишем решение уравнения (16.59):

х = (ЛО - b х²(/)) g(0) + |(ЛО “b х²(т)) - т) с/т.

о

Переходная функция g(z) определяется по линейной части исходного нелинейного дифференциального уравнения при воздействии на нее 1(/). Уравнение (16.60) является интегральным уравнением по типу Вольтер- ра второго рода. Его можно решать методом последовательных прибли­жений, полагая х_о(/) = х(О) и пользуясь таким соотношением для Л-го приближения:

х_к (О = (ЛО - b х²_к__}(О) g(0) + |(ЛО - b х_а²_, (т)) g'(t -x)dx
о

Метод имеет смысл применять только в том случае, когда процесс по­следовательных приближений является сходящимся.

d X 2

Пример 165. Решить уравнение — + х =1 при х(0) = 0. dt

Решен не. Для определения g(z) на линейную часть системы воздействуем единич­ным напряжением —~ - 1 ; g(z) = /; g\t) = 1; g(0) = 0; g'(( - т) = 1. Записываем рекуррен­тное соотношение:

о г ( .3

х,=рт = С х₂ = J(l-T²)^T = ^-—; о о

¹ f* 2/⁵ /⁷

х, = ((1 — (т — т³ /3)*) d т = /--------- +---------- ——.

Г 3 15 63

§ 16.10 Переходные процессы в цепях с терморезисторамн. Мето­дику рассмотрим на примере схемы (рис. 16.6, а). Переходный процесс вызван замыканием ключа К. Полагаем, что температура окружающей

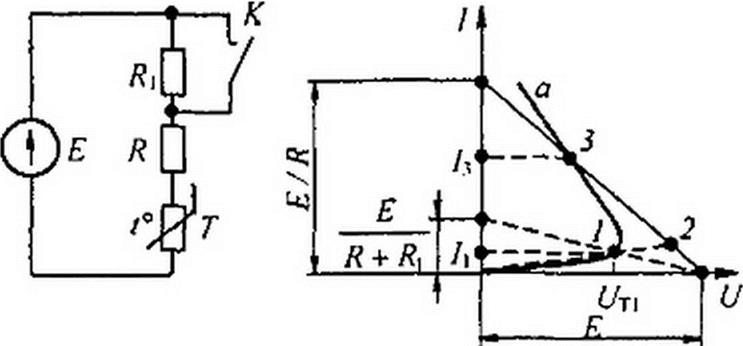
а б

Рис. 16.6

среды 9 неизменна. ВАХ термистора при температуре 9 представлена на рис. 16.6, б кривой а. Установившийся режим до коммутации опре­деляется точкой /, после коммутации — точкой 3. Сразу после коммута­ции сопротивление термистора (он обладает большой постоянной вре- и_т мени) остается равным его сопротивлению до коммутации Rj =— ^L .

¹ А

При коммутации изображающая точка скачком перемещается из положе­ния 1 в положение 2. После этого она по некоторой траектории переме­щается из 2 в 3. Режим в точке 3 будем полагать устойчивым (в § 3.10 [24] разобрано, как исследовать устойчивость этого режима). Переход­ный процесс описывается уравнением теплового баланса

С,.^ + ЦГ-0) = /² Я, , (16.61)

a t

где С₇- --------- теплота, идущая на увеличение теплосодержания тела тер-

d t

мистора; С₇— удельная теплоемкость; Т — среднеобъемная абсолютная температура тела термистора; к(Т -9) — теплота, отдаваемая в окружа­ющее пространство; 1² R_f— теплота, выделяемая в термисторе.

Полагаем, что за время переходного процесса к и С_т практически не­изменны. Сопротивление термистора R_T = (_см., например, [24]);

Д Е

7^— сопротивление термистора при Т ->«>; В-------------------------------------------------------------- , где Д£ —

2 Aj

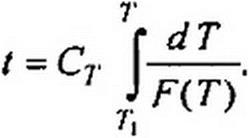усредненная энергия активации; к_} — постоянная Больцмана. Например, для термистора ММТ-1 В = 4600 к и = 5,5 Ом . Из уравнения (16.61) следует, что

(16.62)

Здесь

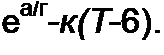Верхний предел интеграла в (16.63) изменяется от 7] до Т_ъ :

_т= в . _ в

' in(/?_r/л„)’ ³ 1п(я_Г1 / я„) ’ ’’ л ■

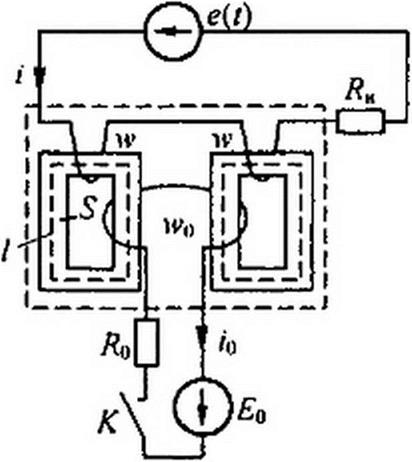
§ 16.11 Переходные процессы в цепях с управляемой индуктив­ностью. Типичный представитель такого класса цепей представлен на рис. 16.7, а. Управляемая цепь образована источником синусоидальной ЭДС е(г) = Е_м sin(со / + <р), двумя обмотками w нелинейной индуктивно­сти, расположенными на двух одинаковых магнитных сердечниках

РЯ_О б

(сечением 5, длиной средней магнитной линии Z), и резистором сопро­тивлением .

Управляющая цепь образована источником постоянной ЭДС Е_о, ре­зистором сопротивлением и двумя обмотками w₀, расположенными на тех же сердечниках. Переходный процесс вызывается замыканием ключа К. При замкнутом К магнитная индукция в левом сердечнике
равна В_т sinco/ + ^₀, а в правом В_т sin <at-B_Q (высшие гармоники не учитываем). Амплитуда синусной компоненты В_т и «постоянная» составляющая B_Q являются медленно изменяющимися функциями вре­мени, влияющими друг на друга.

Учитывая направления намотки катушек, замечаем, что потокосцеп­ление двух обмоток w равно 2 w S В_т sin со /, а потокосцепление двух обмоток w₀ равно 2 w_Q S В_о.

Выразим кривую намагничивания ферромагнитного материала сердеч­ников гиперболическим синусом Н = ash0 В. Используя закон полного тока и формулы (15.13) и (15.12), запишем первую гармонику тока ф у

/ =------- ch р Bq (-J J](jP 2?^)) sin coz. Мгновенное значение медленно

w

изменяющегося «постоянного» тока в цепи управления Q /

io = — sh р В_о В_т). Запишем дифференциальное уравнение для мгновенных значений первых гармоник управляемой цепи:

В_т sin со/ + — R_H ch0 В_о (-j 05_m))sin со/ =

0 ^{dt w} (16.64)

= E_m sin(co t + cp)

и дифференциальное уравнение для мгновенных значений цели управ­ления:

2 Д_{о +} аЦ _{chp р = (|6 б5)}

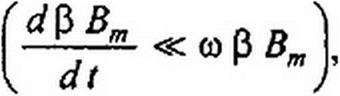0 dt w

Учитывая медленность изменения 0 В_1П во времени из уравнения (16.64) получим уравнение (16.66):

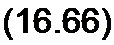т 0 В_т cos со / + п ch 0 Bq (-/ J\ (j 0 B_m)) sin co t - = E_m cosф sin co t + E_m sin ф cosco /;

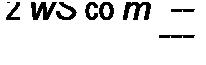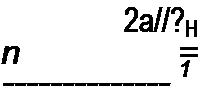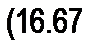Равенство косинусных компонент уравнения (16.66) дает уравнение (16.67), а синусных компонент — уравнение (16.68):

m 0 = Е_т sin ф;

n Ch 0 Bq (-J J, (J 0 B_m)) = E_m cos Ф. (16.68)

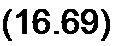Возведем (16.67) и (16.68) в квадрат, сложим и разрешим относитель­но ch0 Bq. Получим

ch0S_o=-^L—

По формуле (16.69) строим зависимость р В_т = /ф 5₀) при переход­ном процессе (рис. 16.8, б).

Обозначим к₀ =-------- ⁵— и перепишем уравнение (16.65) в виде

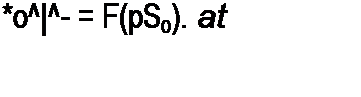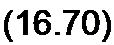Здесь F(P Bq) - Е_о - ch0 Bq Jq(J P B„,). Из уравнения (16.70) ^wo

определим время Л необходимое для нарастания р В_о от 0 до текущего значения р Bq :

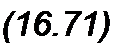dp В_о

ЛР Bq)

Располагая зависимостью р£₀ =/(/), с помощью рис. 16.7, б получим РВ_Л, =/₂G), ^а затем, используя формулу 2 сх /

1_т =------- chр Bq (- j J\(J Р В_т)), строим огибающую амплитуд первой

W

гармоники тока i управляемой цепи /„, - /₃(Г) от времени. По формуле

/₀ = —shp B_qJq(J р В„,) определяем зависимость /₀ = /₄(г). w₀

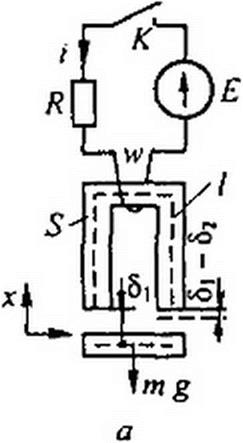
§ 16.12 Переходные процессы в нелинейных электромеханических системах. В качестве примера рассмотрим переходный процесс в элект­ромагните постоянного тока (рис. 16.8, я). Сердечник и подвижная часть (якорь) электромагнита имеют площадь поперечного сечения S, длину средней магнитной линии по пути в стали /. Масса якоря и груза т, кри­вая намагничивания сердечника и якоря Н = J\B) известны (рис. 16.8, б). Через х обозначим изменяющееся расстояние между верх­ней частью якоря и сердечником. В исходном состояниих = 0. В процессе движения якоря зазор равен 5,-х. При притянутом якоре х = 8_}-8₂ (8₂ — толщина тонкой немагнитной прокладки; она может и отсутство­вать, тогда 8₂ = 0).

Переходный процесс после замыкания ключа К при / = 0 состоит из трех стадий:

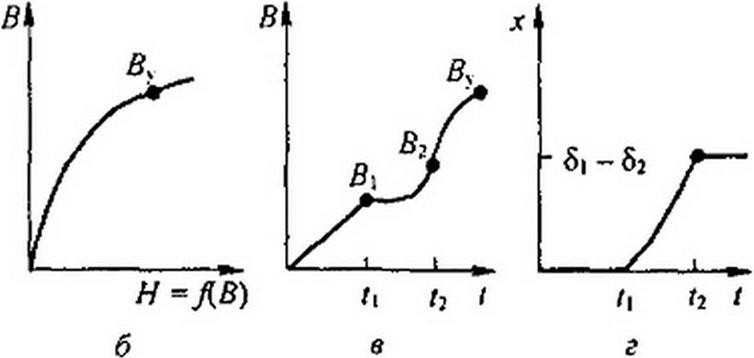
1, От t = 0 до t - /| при неподвижном якоре (х = 0) сила тяги возра­стает от 0 до величины, равной весу якоря и груза, а индукция — от 0 до В| (рис. 16.8, в, г).

2.3а время от / = /, до / = /₂ якорь притягивается к сердечнику, зазор изменяется от х = 0 до х = 8] -8₂, а индукция — от В_} до В₂.

3. При t>t₂ и неизменном х индукция В возрастает от В₂ до уста­новившегося значения В_у.

Сила тяги электромагнита может быть определена как произведение удельного продольного тяжения вдоль магнитных силовых линий в воздушном зазоре (оно равно плотности магнитной энергии в единице объема Z?²/(2p₀)) на площадь поперечного сечения двух воздушных зазоров 2 S:

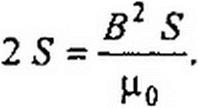По закону полного тока, И I + 2 (8₍ -х) =/ w, но Н = f(B\ а

В I 2 В

, поэтому ток / = — f (В) +---------------------------------------------- (8] - х).

ц₀ ^w

Процесс описывается двумя совместными уравнениями:

для электрической части системы

wS — + R\~ f(B) + ^~(^-x)] = E; (16.72) аЦ wp₀ J

для механической части

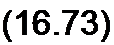d²x В² S

m —— + m g =

dr Po

В первой стадии якорь неподвижен, х = 0 и нарастание В от 0 до В_} определяем по уравнению (16.72), причем —— ~т g и В, « ^т $.

Но ¹ V S

Во второй стадии уравнения (16.72) и (16.73) должны быть решены со­вместно на ЦВМ. Стадия закончится, когда х станет равным 3[ -8₂.

В третьей стадии процесс описывается уравнением (16.72) при х = 8|-8₂; В_у определяем из уравнения

/(S )/ + —2 8₂ =
Mo ^R

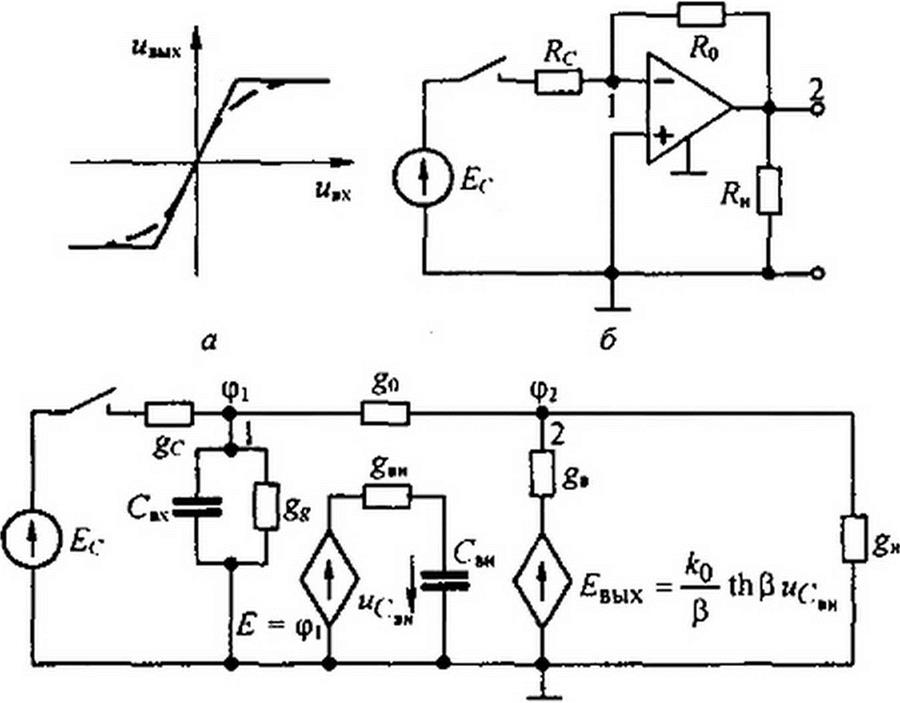
§ 16.13. Переходные процессы в схемах с управляемыми источниками с учетом их нелинейных и частотных свойств. Схемы с управляемыми источниками выполняют очень часто на ОУ. Выходное напряжение ОУ нелинейно зависит от входного напряжения (рис. 16.9,о). Эту зависимость можно аппроксимировать гиперболическим танген-

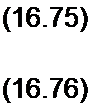
An 1

женин только первый доминантный полюс, то K(j <о)=------------------------------------------------------------------------------- —--------------------------------------------------------------------------------- . Через coj -------------------------------------------------------------------- ---------------------------------------------------------------------------------- обо-

1 + j о х_вн т_вн

значим частоту, при которой модуль K(j а) уменьшается до (затухание в 3 дБ).

Инерционные свойства ОУ будем описывать некоторой вспомогательной цепью, состоя­щей из источника управляемого напряжения, резистора /?_вн и конденсатора емкостью С_вн (^хвн ⁼ ^ян С_вк )-

Макрометод описания переходных процессов проиллюстрируем на схеме инвертиру­ющего повторителя напряжения (рис. 16.9. о). Сигнал £<• поступает на инвертиру­ющий вход ОУ, сопротивление которого по отношению к заземленному входу ОУ а емкость — С_вх. Неинвертирующий вход заземлен, поэтому параметры его нс учитыва­ем. Расчетная схема изображена на рис. 16.9, в. Вместо сопротивлений на ней указаны про-

водимости. Потенциалы узлов / и 2 обозначены ф| и <р2- ЭДС на выходе ОУ " у Р и_См , где и_с

Переменными состояния являются напряжения на конденсаторах «с . ⁼Ф1 ^{и и}С ■ Запишем уравнение для вспомогательной цепи;

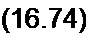_ I

di T_eii

Составим два уравнения по методу узловых потенциалов относительно ф| и <Р2 ^:

Ф1 (РС_ВХ + g_A> +g_c +go)-^2 go = ^£С g(S

An

- Ф1 go ⁺ Ф2 (£o ⁺ SB ⁺ 8H ) = ~SB th P »c’ •

p •"

Из (16.76) определим ,

-ёв + ё0 Ф]

<р₂ = S. (16.77)

£0 + ёв ⁺ ёН

Подставим ф2 ^в (16.75) и заменим р С_8Х Ф] на С_вх —Затем запишем ^th Р “<-»н ~ Р ^и<”.и J® ^WC._H ^{где dt}

/(р “С_1И ) = 1 - “ (р «С,_и У + 1р «С'_1И У “ ““ 1р ^Ис._и У + -

В результате с учетом (16.74) получим два уравнения относительно 0и_с и 0ф₍:

В К

^P^MC_W 1 _а In

——К- =------------------ ₽ w_c + 0_Ф];

^Т ВИ ^Т8Н

~“7~ = -а 0 и_с,_н - b р ф) + Е₍
и¹ ^вх

Здесь

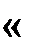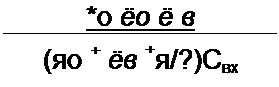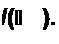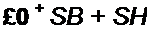При числовых подсчетах —~ и ток во вспомогательной цепи схемы не должны пре- dt

вышать максимальных паспортных значений ОУ, в противном случае параметры схемы должны быть скорректированы.

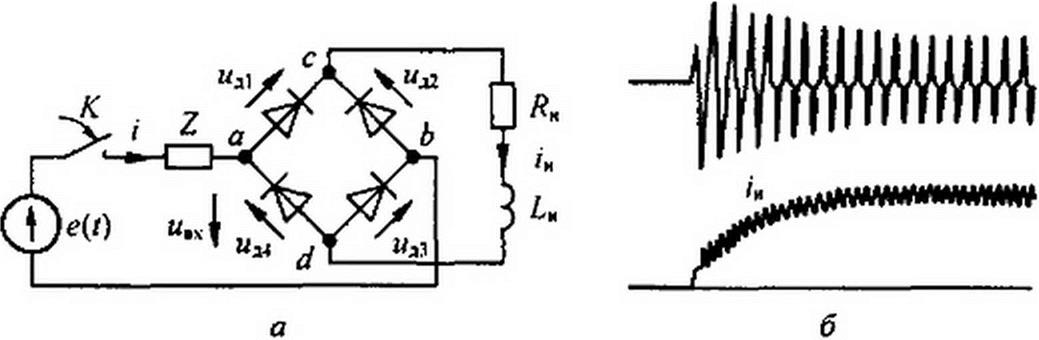
§ 16.14. Переходные процессы в мостовой выпрямительной схеме с предвклю- ченными сопротивлениями в цепи переменного тока. В схеме, приведенной на рис. 16.10. а, к источнику синусоидальной ЭДС Е_т sin(w / + ф) подключается цепь, со­стоящая из комплексного сопротивления Z = R + J<aL и последовательно соединенного с ним выпрямительного моста с резистором R_H и индуктивностью £_н на выходе. Пере­ходный процесс рассматриваем, полагая, что L^IR^ з> Т и LIR<T, где T = \!f, а f — частота источника ЭДС.

В качестве иллюстрации на рис. 16.10, б представлена осциллограмма переходного процесса при /?_н = 4 Ом, L_a = 0,4 Гн, R = 20 Ом, / = 50 Гн. Из рисунка видно, что на­пряжение на входе моста w_BX = и_аь плавно уменьшается по амплитуде и одновременно с этим плавно нарастает среднее за полпериода значение тока /_н. Длительность переходно­го процесса составляет примерно 9 Г, что значительно меньше длительности переходно­го процесса 3£_Н/Л_Н=15Г при подключении последовательно соединенных R_H и £_н непосредственно к источнику постоянной ЭДС. Форсирование переходного процесса про­
изошло благодаря динамическому перераспределению напряжения источника ЭДС между сопротивлением Z и входом выпрямительного моста.

При расчете параметров переходного процесса воспользуемся методом медленно из­меняющихся амплитуд токов и напряжений на злементах цели переменного тока и мед­ленно изменяющихся постоянных составляющих токов и напряжений на элементах цепи выпрямленного тока.

Вольт-амперную характеристику каждого диода в схеме опишем

(16.78)

Напряжения на диодах и токи через них служат связующим звеном между процесса­ми в цепях переменного и выпрямленного токов. В установившемся режиме напряжения надиодах и_д,(/) = и_д3(/), и_л2{Г) = и_д4(/) = и_а\(у - Т/2) являются периодическими функция­ми времени и могут быть представлены рядами Фурье:

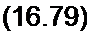Мд] = -U _до + У am sin СО / -f- U 2 a SIП 2 <0 t + U 2 _с cos 2 со t +
+ U_3x sin3 co i + U_3c cos3 «/ + ...

М_д2 = дО “ ^дт sin co / +1/₂₁ sin 2 <o / + (7₂₁. cos 2 о / -
-U_3x sin3e)/-{/_3c cos3 OZ + ...

При переходном процессе все амплитуды слагаемых рядов медленно изменяются во времени. Сначала ограничимся учетом постоянных составляющих рядов и первых гармо­ник, после этого приближенно учтем наличие высших гармоник и их влияние на переход­ный процесс. Влияние высших гармоник на ток /_н учитываем с помощью коэффициента К], а наток i— коэффициентом К^. Считаем, что в каждом плече моста п диодов. Урав­нения для цепей выпрямленного и переменного токов соответственно имеют вид:

L_H ^-~- + R_H /_н +л(д_д1 +и_д2) = 0; (16.80)

a t

L — + R i + п (и_а} -ы_д2) = Е_т sin(ci) 1 + ф). (16.81)

d {

Если не учитывать четные гармоники рядов, то

^u dc ~ ^{п + и}д1) = ”2 л (7_д0 = -2 UQ.

Здесь ~2Uq — постоянная составляющая напряжения на зажимах de моста. В свою очередь напряжение u_afl на зажимах моста без учета третьей гармоники

^л ) = ² « sinco/ = 2U_m sin со/,

где через 2 U_m обозначена амплитуда первой гармоники на входе моста.

Выразим токи /_н и / через U_д0 и и_лт sinco/. С этой целью подставим укороченные ряды для Мд) и и_а2 в формулу (16.78):

=/, ₊,₂ = а (е'^А,/ди _с^м/а-’^5пи/ -1 _{+ е}'^А^ _e’^M/^^sintoZ -!)=
= 2a(c^/>u*' J_obbU_a„)K^l)-

Л(;_дт5юы/ -ЛГ/_ДИ sinaf | е — е / л 2 —

-A A е~^1>1'^л0 (-j J|(j b U _ат)) К₂ since/= i_m sin о/.

Медленно изменяющуюся «постоянную» составляющую тока /_н обозначим через )_но . Из уравнения (16.80) для нес следует:

С. Т7Т ^{+ Л}» = ^{2 и}‘0- <¹⁶-⁸⁴>

а t

Затем учтем медленность изменения амплитуд первой гармоники напряжения U_m и тока 1_т во времени « (л 1_т и ^^т- (t>U_m и вместо (16.81) запишем уравне- di dt

ние:

(2 U_m + R /_т ) sin w I + w L /_п> с os о / = Е_П) sin(co/ + <p). (16.85)

Разобьем его на два уравнения (для синусных и косинусных компонент), возведем каждое из них в квадрат, сложим и придем к уравнению вида

(2W„+«/„)²+(o£/_m)²=£². (16.86)

Разрешим (16.86) относительно 2 U_m:

2 U„ = ^E²-(_aL/_m)² - R 1„ (16 87)

и примем во внимание следующее.

1. При описании ВАХ диодов формулой (16.78) токи / и /_н оказываются выраженны­ми через показательную и бесселевы функции (см. (16.82) и (16.83)). За счет резкого изгиба ВЛХ диодов вблизи начала координат значения аргументов этих функций при пе­реходном и установившемся режиме выпрямительной схемы оказываются значительно больше 5; например, величина bU_m в начале переходного режима может оказаться рав­ной 20. Но уже при х>5 бесселевы функции Jo(j х) и (-yJ|(yx)) практически равны друг друг}' и могут быть заменены асимптотическим выражением с^х /2 их. Кроме того, при b U_т >8 можно в формуле (16.82) не учитывать I. при этом из (16.82) и (16.83) сле­дует, что /„, =1^2._/н0.

*1

2. Рассмотрим понятие о средних за полупериод Г/2 значениях следующих вели-

чин: тока /_нОс, напряжения Д/_дОс. амплитуд разом:

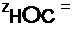тс

с

2 К->

Рассчитаем величину 2К₂/К\ в выражении 1_П1 -—^-/_hq. Исходим из того, что электрический заряд, проходящий по цепи переменного тока за полупериол Т/2, по закону сохранения заряда равняется заряду, прошедшему за то же время по цепи выпрям­ленного тока. т. е. должно выполняться соотношение

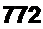772

jf_mc sina>tdt = J/_hOc dt

или

_7_ .

тс ~ ⁽к0с<

отсюда /_wc = 1,57j_hOc » 2К₂1К\=\,52.

Зависимость между плавно изменяющимися значениями 1_т\ и /_hq примем такой же, как для дискретных значений 1_тс и '_Н0с (так как эта зависимость выполняется для лю­бого полупериода переходного процесса).

3. Оценим влияние четных гармоник на выходе моста на работу схемы. Сначала выясним, влияют ли они на величины средних за полупериод Г/2 напряжения U_дОс и

заряда:

2 ^т 2 ^Tl2

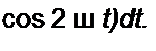^дОс=«у Jta)⁺«д2)<^/' = "26'_д0с-лу \(2и_2з sin2a/ + 2t/_2e О Q

Так как половине периода на частоте f соответствует полный период на частоте 2 /, в установившемся режиме работы четные гармоники на выходе моста не оказывают вли* яния на £/_яОс и среднее за полулериод значение заряда. При медленно изменяющихся амплитудах влияние четных гармоник на значения U_aQc и электрического заряда за полупериод не­велико. Отметим, что четные гармоники способствуют увеличению времени нахождения диодов в проводящем состоянии.

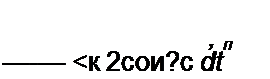4. Определим теперь соотношение между средними за полупериод значениями U_amc и U_aQc при переходном процессе. Если бы диоды имели идеально прямоугольные ВАХ (см. рис. 1539, в), то при протекании токов в них не было бы тепловых потерь, а энергия, доставляемая за полупериод со стороны входа ab моста схемы рис. 16.10, а источником питания схемы на первой гармонике, была бы равна энергии, которую со стороны выхода cd мост доставил бы за то же время в цепь выпрямленного тока, т. е. выполнялось бы соотношение:

7/2

п |2 t/ддас sin© t I_mc sin© / dt =

_m ° 0688)

= " ((²О_аое⁺²О_г„_с sin(2o>/+p))(/_nOC +/_Imc sin(2m/ + 0 + v))<//.

0

Здесь 2U2_mc — среднее за лолупериод значение амплитуды, ар— фазы напряже­ния второй гармоники на выходе моста; /_2л)С — среднее за полупериод значение ампли­туды, а Ц/ — фазы второй гармоники тока на выходе моста:

., Г~2 ТТ? п , 2 п (J 2m с 2 (a L

U2m^^_2sc*U₂ ₽=arctg——, /₂„,_с - _v = arctg—

"²“' /л² + (2 _Ю Д„ )^{2 Я}»

После интегрирования, сокращения на л и Г/2 получаем:

опте 1 тс УдОс 6<0с ⁺ тс тс со$у = 2С/_д0с/_мОс К₃, (16.89)

где

. ^2тс¹2тс^^

К. j = 1 + ——■ ~

2 Uдо с нОс

С помощью коэффициента Кт. в выражении (16.89) учтены тепловые потери в резне- торе от тока второй гармоники. Коэффициент зависит от величины /?_н, L_H и и

при L_H/R_H » Т равен примерно 1,10-1,18 (примем его равным 1,15). С ростом L_h/Rh

коэффициент Кз уменьшается. Учитывая, что /_Л)С = 1,57 /_нОс , из (16.89) определим

21/,₀ = = 1.365

5. Оценим влияние третьих гармоник напряжения на зажимах ab моста sin3 со / + Uj _с cos3c>/) на работу схемы. От третьих гармоник напряжения через

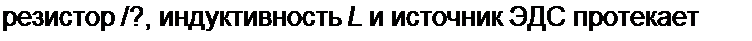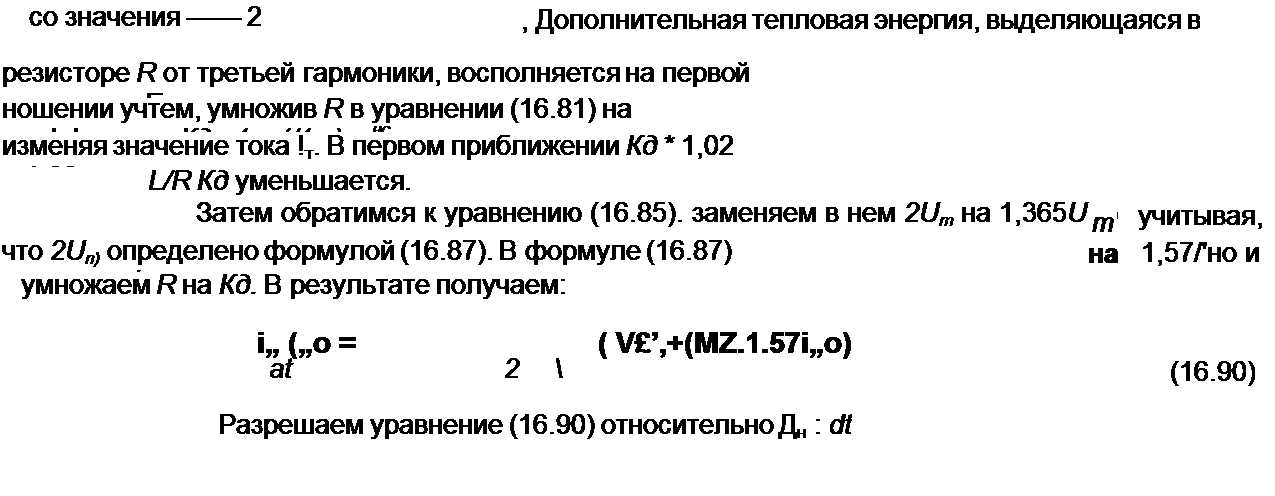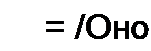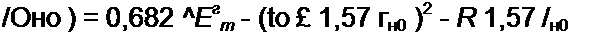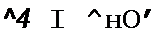В (16.91) разделим переменные и получим формулу для определения текущего значе­ния времени /_тск, соответствующего текущему значению тока /_но_тек . полагая, что при / = о /_но = 0:

^'нОтек

'тек=^н J (‘6.93)

0 /Оно)

Установившееся значение тока '_н0у получим, приравняв нулю /Оно): _ _

/_н0 у - ~---------- —...... - —- .

у (1,57 to L}¹ + (1,57 R Кд + 1.466 R_n)²

Начальная фаза Ф источника ЭДС на входе схемы на рис. 16.10, а при L_H/R_H >Т может повлиять на длительность переходного процесса на величину порядка (0,5-1,0) Т.

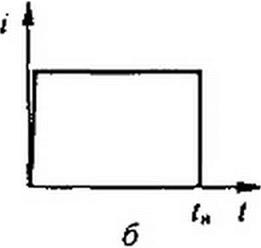
§ 16.15. Перемагничивание ферритовых сердечников импульсами тока. В устрой­ствах вычислительной техники в качестве запоминающих элементов применяют миниатюр­ные ферритовые сердечники различной формы, в частности кольцевые с внешним диаметром порядка 1 мм из материала с прямоугольной петлей гистерезиса (ППГ). Через отверстия в них пропускают проводники, являющиеся одновитковыми обмотками (на рис. 16.11, а показан только один проводник). При записи информации по одному из про­водников пропускают прямоугольный или почти прямоугольный импульс тока (рис. 16.11, 6) длительностью в несколько десятков наносекунд или микросекунд. Под дей­ствием этого импульса сердечник перемагничивается. Хотя в ферритовом сердечнике и от­сутствуют макроскопические вихревые токи (в нем нет замкнутых токопроводящих кон­туров, выполняющих функции вторичных обмоток трансформатора), перемагничивается он все же не мгновенно.

На длительность процесса перемагничивания сердечника при высоких скоростях перемагничивания решающее влияние оказывает магнитная вязкость, которая создает внутрен­нее поле трения. Последнее зависит от значения и скорости изменения намагниченности, а также от превышения воздействующей напряженности поля над коэрцитивной силой.

При математическом описании тормозящего действия магнитной вязкости исходят из уравнения

(16.94)

где Hq — напряженность поля, при котором происходит перемагничивание феррита с ППГ (Яо несколько больше коэрцитивной силы Н_с по статической петле гистерезиса; #0^HaxoW опытным путем для каждого типа феррита); Я_вн =iw/i— напряженность внешнего поля, вызванная током i (w — число витков; / — длина средней магнитной

линии). Член а — учитывает тормозящее действие магнитной вязкости. Множитель , dl

. где к — некоторый коэффициент; J — текущее значение намагничен­ности; J_s — намагниченность насыщения.

Решим уравнение (16.94) относительно dJ / ^/.заменив J на индукцию В, a 3_А — на индукцию насыщения B_s . Получим уравнение относительно В:

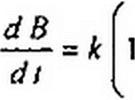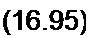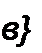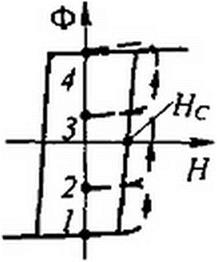
Это уравнение с разделяющимися переменными. Из (16.95) следует, что для перехода из точки / в точку 4 (рис. 16.11, в) под действием импульса тока / длительностью г_н должно выполняться соотношение

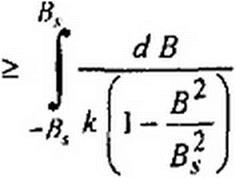j(#вн - H§)dt < М, то изображающая точка из положения / после прекра-

0

щения действия импульса перейдет в точку 2 или 3 или им подобную (конечное состоя- ние зависит от J (/У_ЙН - H^dt и амплитуды импульса тока). Из состояния / в состояние О

4 сердечник может быть переведен и иным путем — путем воздействия на него несколь­кими следующими друг за другом импульсами одинаковой полярности, для каждого из 'к

которых |(Я_ВН - Ha)di < М. После первого импульса рабочая точка перейдет из поло- 0

жения /, например, в положение 2, после второго из положения 2 — в положение 3, затем из положения 3 — в положение 4.

§ 16.16. Фазовая плоскость и характеристика областей ее применения. Качествен­ное исследование процессов в нелинейных электрических цепях, описываемых дифферен­циальными уравнениями первого и особенно второго порядка, в ряде случаев производят с помощью фазовой плоскости.