Коэффициент пропорциональности L^s между потокосцеплением и током называют индуктивностью рассеяния первичной обмотки', Lqs зависит от числа витков и конструкции обмотки.

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Принимают также, что потокосцепление ф_2л. потока Ф_2т обмот­кой пропорционально току вторичной цепи /₂;

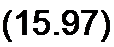^2л - ^W 2 ^2л “

Коэффициент пропорциональности L_2s между потокосцеплением обусловленным потоком рассеяния Ф_3а., и током /₂ называют ин­дуктивностью рассеяния вторичной обмотки, L_2x зависит от числа витков и конструкции вторичной обмотки.

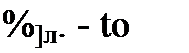Индуктивное сопротивление первичной обмотки, обусловленное по­током рассеяния Ф_ь,

(15.98)

Аналогично, индуктивное сопротивление вторичной обмотки, обус­ловленное потоком рассеяния Ф_2л,

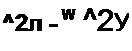(15.99)

Пусть R_} — резистивное сопротивление первичной обмотки; R₂ — резистивное сопротивление вторичной обмотки; Z_H — сопротивление нагрузки.

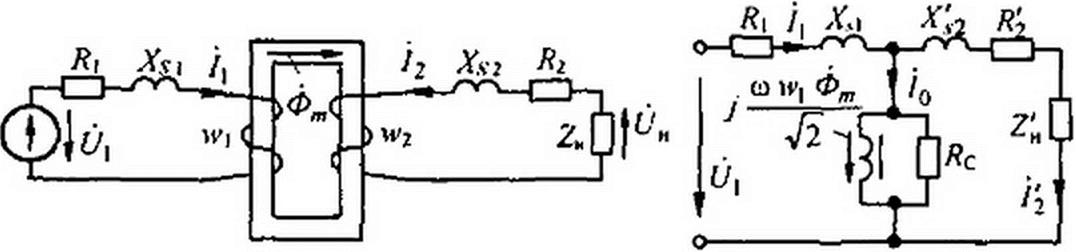
На рис. 15.52, а изображена схема того же трансформатора, что и на рис. 15.51, в, но на ней резистивные и индуктивные сопротивления, обус­ловленные потоками рассеяния, представлены отдельно выделенными R_}, Л|_А., /?₂, JV_2?. Запишем уравнение по второму закону Кирхгофа для обеих цепей.

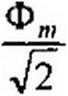
Для первичной цепи

(15.100)

для вторичной цепи

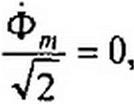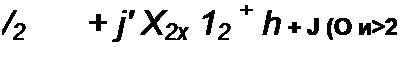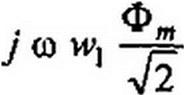
— напряжение, численно равное ЭДС, наводимой в

обмотке W] основным рабочим потоком Ф^,. Деление Ф_т на V2 объяс­

няется переходом от амплитудного значения к действующему. Аналогично Ф

ytowj—— напряжение, численно равное ЭДС, наводимой в Аг

обмотке w₂ основным рабочим потоком Ф_л?.

Обозначим ток при холостом ходе трансформатора через /₀. МДС трансформатора при холостом ходе равна /₀ w_x. МДС трансформатора при наличии тока /₂ составляет +/₂ w₂. Трансформаторы конст­руируют обычно таким образом, что падения напряжения Ц и j /, Х_1х

Ф

были много меньше, чем падение напряжения со wj —Л-. Если это учесть, V2

то для правильно сконструированных трансформаторов уравнение (15.100) запишем так:

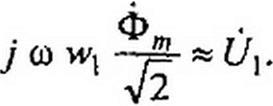(15.102)

Уравнение (15.102) справедливо как при холостом ходе, так и при на­грузке, т. е. при переходе от холостого хода к режиму работы при нагрузке поток Ф_т практически остается неизменным по модулю.

Но если в этих двух режимах поток Ф_л; один и тот же, то должны быть равны и создающие его МДС, т. е.

(15.103)

Поделив обе части равенства на w,, получим

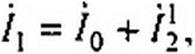(15.104)

где

₂ -~1₂ •

И'[

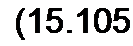Таким образом, ток первичной цепи может быть представлен как геометрическая сумма двух токов: тока холостого хода /₀ и тока /₂. Ток Г₂ называют приведенным (к числу витков первичной обмотки) вторич­ным током. Он численно равен току /₂, измененному в раз.

Кроме того, в правильно сконструированных трансформаторах паде­ния напряжений /₂ /?₂ и у/₂ Х_2х малы по сравнению с ja>w₂ поэтому из уравнения (15.101) следует, что

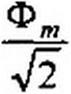Ф

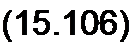j (j) W₂ ~=- is -U_н.

Если почленно разделить (15.102) на (15.106) и перейти к модулям,

(15.107)

т. е. отношение напряжения на входе трансформатора к напряжению на его выходе (на нагрузке) приблизительно равно отношению числа вит­ков первичной обмотки к числу витков вторичной обмотки.

В правильно сконструированных трансформаторах при нагрузке, близ­кой к номинальной, ток Z_o составляет 1-10 % тока поэтому уравне­ние (15.103) можно приближенно представить так:

/j и-) * -/₂ w₂.

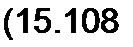Между модулями токов и /₂ при нагрузке, близкой к номиналь­ной, имеет место следующее приближенное соотношение:

/j / /₂ ~ W₂ / W| ,

т. е. ток /( почти пропорционален току Z₂- Эта пропорциональность немного нарушается за счет тока холостого хода /₀.

В резистивных сопротивлениях вторичной цепи выделяется энергия, которая переносится магнитным потоком из первичной цепи во вторич­ную и восполняется источником питания схемы. На рис. 15.52, б изоб­ражена схема замещения трансформатора со стальным сердечником. Для ее обоснования уравнение (15.101) умножим на /м>₂, заменим в нем ток /₂ на Г₂ (W| / w₂) в соответствии с (15.105) и у всех слагаемых урав­нения изменим знаки. В результате получим

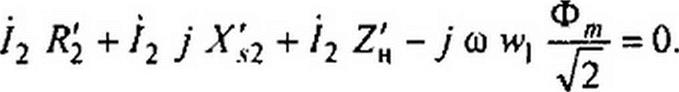Приведенные сопротивления

^ = /?₂(w,/w₂)²; Л;₂=Х,₂(и-₁/и'₂)²; Z>Z_K(W,/_W2)².

Схема (рис. 15.52, б) удовлетворяет уравнениям (15.100), (15.103) и (15.109).

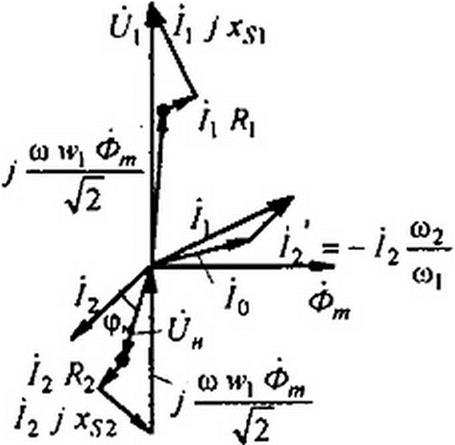
§ 15.69 Векторная диаграмма трансформатора со стальным сер­дечником. На рис. 15.53, а изображена векторная диаграмма при индук­тивной нагрузке Z_H = R_H + j

Построение диаграммы начнем с тока /₂, расположив его произволь­но. Под углом <р_н =arctg%_H / R_H к нему расположим вектор напряжения на нагрузке U_H. Прибавим к вектору (У_н векторы /₂ /?₂ и /₂ J %. si- Сум­ма падений напряжения во вторичной цепи равна нулю, что дает возмож­ность построить вектор j « w₂ ~г^г- Далее строим вектор <Ь_т (он на 90°

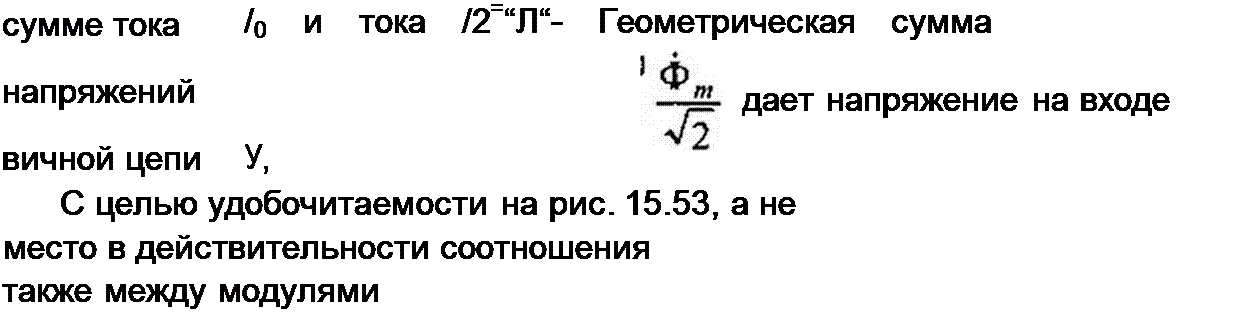
Произведение 0 В_т = 5.75 • 1,22 = 7,02.

Пр кривой (рис. 15.51, б) при Р 8_т - 7,02 находим н'|/_g/(a / *2)= 185. а/ <2/^ =0,71 -0,25 ^2 /250 = 10’³. Следовательно, /_g= 0,185 А.

Масса сердечника при плотности 7,8 г/см² = 7,8-2,2 с.м² ■ 25 см = 0,428 кг.

табл. 15.2 находим p_{i 0} = 1,6 Вт/кг; Р\ ₅ = 3.6 Вт/кг, л = 5,69 lg(3.6/1,6) * 1,13.

Удельные потери в стали при В_т * 1.22 Тл р_с = 1,6 - 1,22^м3 -1 = 2,1 Вт/ кг. Полные по­тери в сердечнике массой 0,428 кг Р_с - 0,428 2,1 = 0,9 Вт. Ток. обусловленный потерями р

встали. 1_С * — = 0,9/15 = 0.06 А. Ток холостого хода /₀ практически равен току /_р. ^1

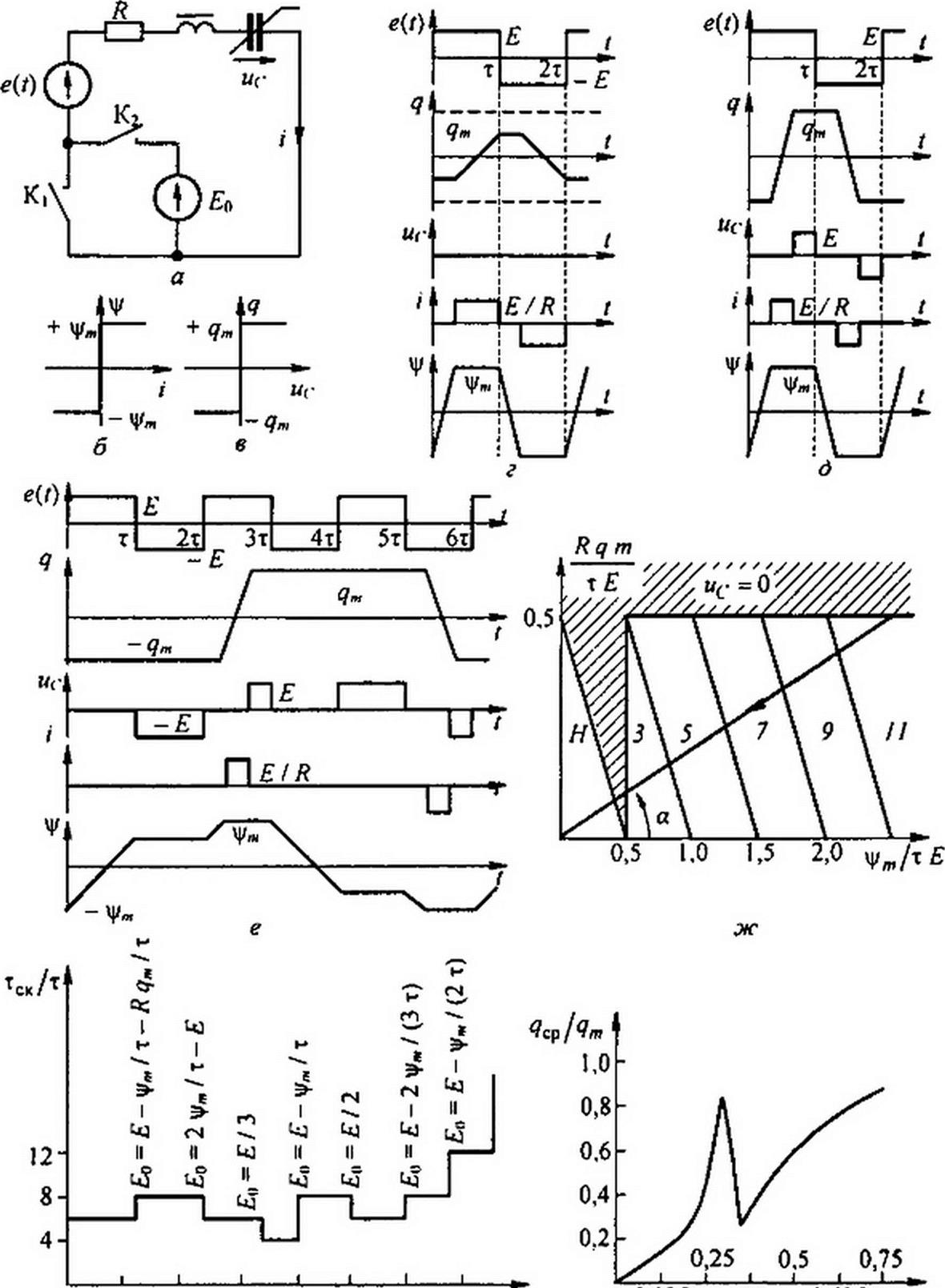
§ 15.70 Субгармонические колебания. Многообразие типов дви­жений в нелинейных цепях. Субгармоническими называют колебания, период которых Г_ск больше периода Г = 2т вынуждающей силы е(/). Число к-Т_ск/Т характеризует порядок субгармонических колебаний (СК). В цепи рис. 15.54, а с нелинейной индуктивностью и нелинейным конденсатором, имеющими идеально прямоугольные характеристики

0,1 0.2 03 0,4 0,5 0,6 0,7 0,125 0,375 0,625 _£q/_£

и

Рис. 15.54

(рис. 15.54, б, в) и резистором £, при воздействии ЭДС е(/) - ±£. в виде меандра (рис. 15.54, г) (а в дальнейшем также еще и постоянной ЭДС £₀) возникают СК нечетного порядка.

Обозначим а - 2 /(т £) и b = 2 R q_m /(т £). Сначала рассмотрим

работу схемы при замкнутом К₁ и разомкнутом К₂ случае, когда дей­ствует только е(г) = ±£. При b > 1 и а < 1 возникает тип движений, по­казанный на рис. 15.54, г (для этого рисунка а = 0,25 и 6 = 1,5), когда Т = 2 т и и_с = 0 в течение всего периода Т.

При b < 1 и a + b < 1 тип движений (назовем его тип Н) иллюстриру­ет рис. 15.54, д (для этого рисунка а = 0,25 и 6 = 0,5), период 7' = 2т. Для существования СК в цепи (рис. 15.54, а) необходимо, чтобы а>1, 6 < 1. Порядок к равен сумме смежных чисел натурального ряда, в ин­тервале между которыми находится сумма а+ 6.

Так, для существования колебаний третьего порядка необходимо, что­бы 1<а + 6<2. Физически СК возникают потому, что за время т пото­косцепление у нелинейной индуктивности не успевает измениться на величину 2\|/_w. Условие 6<1 означает, что перезарядка нелинейного конденсатора на 2 q_m должна происходить за время, меньшее т.

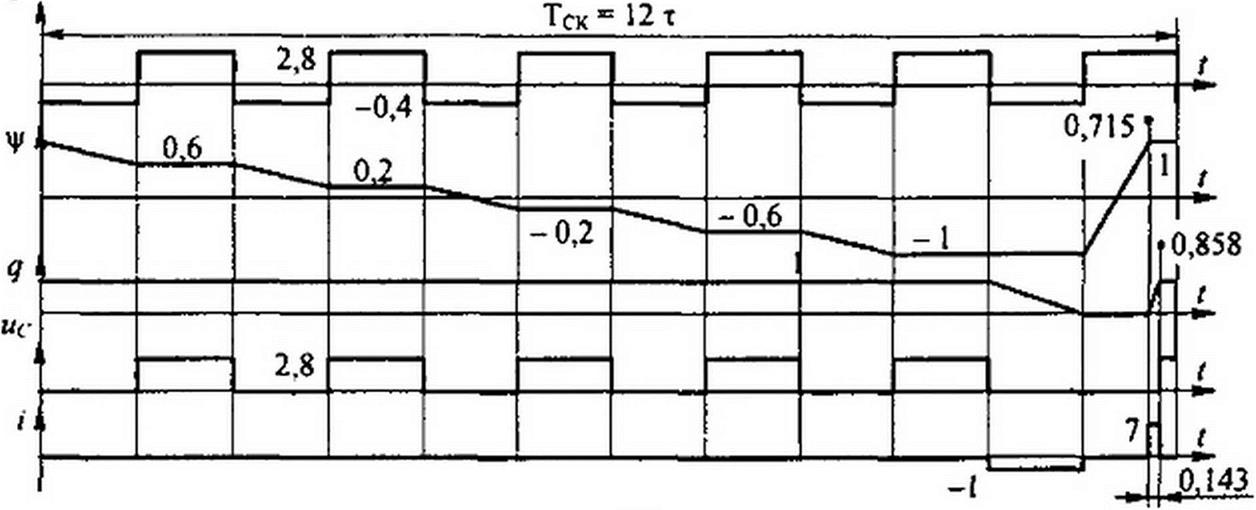
Графики ЭДС e(z), заряда q_y напряжения на конденсаторе w_r, тока i и потокосцепления V при СК третьего порядка (6 = 3, а = 1,25, 6 = 0,5) изображены на рис. 15.54, е. При построении кривых учтено, что увели­чение заряда может иметь место только после того, как Ц/ достигло зна­чения а уменьшение заряда — только после того, как достигло значения -у_т-

Дадим пояснения к кривым на рис. 15.54, е. Период СК третьего по­рядка составляет шесть интервалов длительностью т. К началу первого интервала е(г) = £, заряд q = -q_m и потокосцепление у = -За пер­вый интервал времени длительностью т \|/ изменяется от до 0,6 Так как V не достигло значения y_w, то перемагничивание сер­дечника осталось незаконченным. Во второй интервал времени е(/) = -£ оказывается приложенной к нелинейному конденсатору и_с = -£. В тре­тий интервал времени под действием ЭДС е(/) ~ Е происходит три каче­ственно различных процесса. Сначала заканчивается перемагничивание сердечника нелинейной индуктивности, когда потокосцепление у изме­няется от 0,6 у_п, до (на это затрачивается время 0,25 т ). После это­го за 0,5 т заряд нелинейного конденсатора изменяется от -q_nl до q_m (при этом по цепи течет ток £/ £); в оставшуюся часть времени третье­го интервала (1 —0,25 — 0,5) т = 0,25 т на нелинейном конденсаторе появляется напряжение и_с = £. В последующие три интервала времени каждый длительностью т имеют место процессы качественно такие же, что и в трех рассмотренных, но движения происходят в обратном направ­лении.

Диаграммы возможных типов движений в схеме (на рис. 15.54, а), когда в ней действует ЭДС е(г) = ±£, изображены на рис. 15.54, ж. Заштрихованная область и_с = 0 соответствует типу движения по рис. 15.54, г, область Н — движению по рис. 15.54,6, области 3, 5, 7, Р, 11 — это области субгармонических колебаний соответствен­
но 3-11-го порядка. Если на рис. 15.53, ж провести из начала координат прямую под углом а к оси абсцисс (tga = R на рисунке tga = 0,2) так, чтобы она прошла через все области, то при плавном увеличении Е изображающая точка будет двигаться в направлении стрел­ки, последовательно проходя области 11, 9, 7, 5, 3 и_с = О, Н, т. е. при этом будут получены 7 различных типов движений и все они будут устойчи­вы. Переход из предыдущей области в последующую обусловлен невоз­можностью при измененной Е осуществить смену состояний, характер­ную для предыдущей области.

§ 15.71 Определение условий перехода от одного типа движений к другому. Хаос субгармоник. Рассмотрим теперь СК в схеме рис. 15.54, а, когда в ней кроме ЭДС в виде меандра действует еще и постоянная ЭДС £₀ (ключ К₂ замкнут. разомкнут).

Величину Е_о будем в дальнейшем изменять от 0 до значения £. Полагаем сначала, что все возникающие при этом типы движений будут устойчивыми.

Суммарная ЭДС в цепи е в положительный полупериод равна £ + £₀, в отрицатель­ный -£ + Е_о. Поэтому процесс перемагничивания и перезарядки в положительный полу­период происходит быстрее, чем в отрицательный. Для иллюстрации процессов времен­ными графиками положим £ = 1.6 В. /? = 0,4Ом; т = I с; у_мж|В*с; q_m = I К.

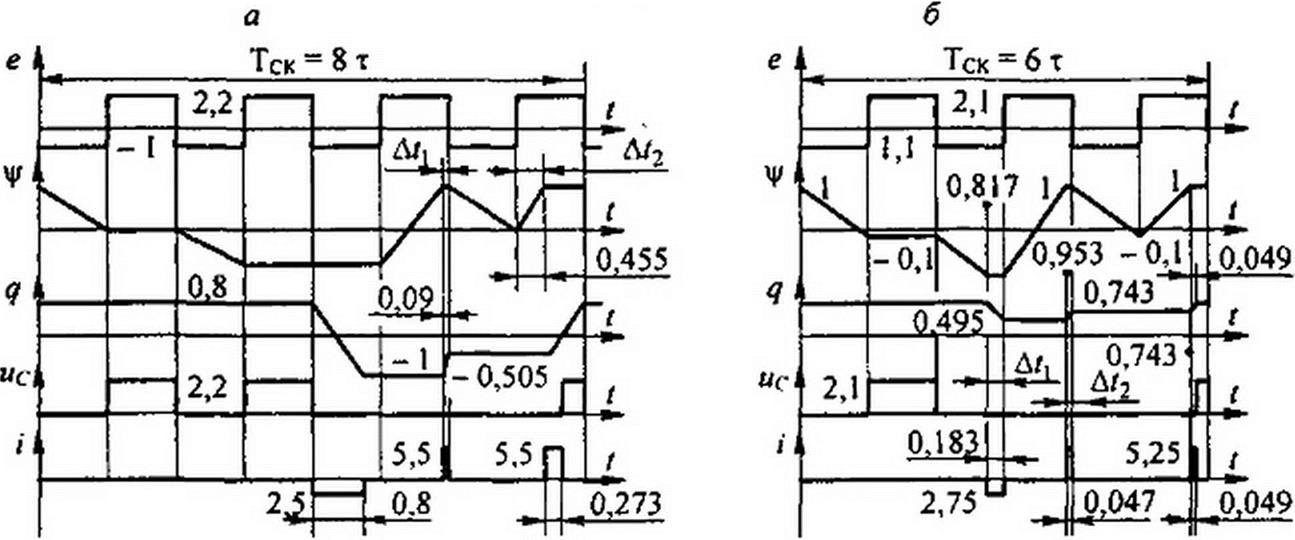
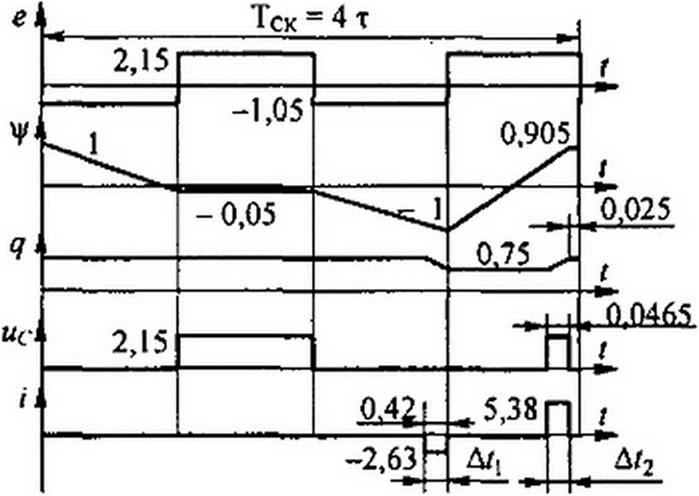
На рис. 15.55, a-ж приведены изменения ЭДС е, V» q, и_с, i в функции времени для нескольких значений £₀: а—при £_о=О.2; б—при £_о=0,3; в—при £_о=О,6; г — при £_о=О,5; д— при £₀ = 0,55: е— при £_о=О,8; ж — при Eq = 1,2 В.

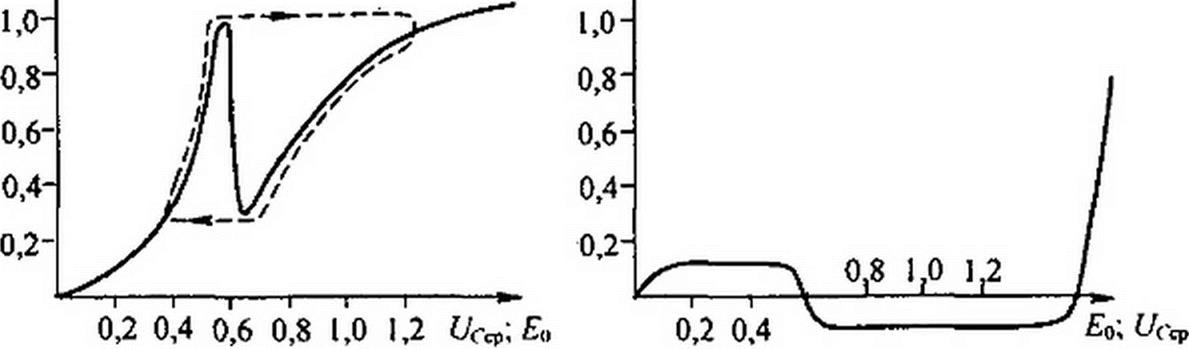
Используя построения и при других значениях £₀, можно получить графики зависимости среднего за период субгармонического колебания Т_ск значения заряда <?_ср =— jqdi (рис. 15.55, а) и среднего за период СК потокосцепления нелинейной

^Гс* о _г

индуктивности ц/_ср ------------- Jyrf/ (рис. 15.55. б).

По оси абсцисс рис. 15.55, а и б отложена постоянная составляющая напряжения на конденсаторе Ue ср, которая в каждом рассматриваемом режиме равна постоянной ЭДС Eq.

При Eq-E (в примере при £₀ = 1,6 В ) <?_ср становится равным q_m (в примере 1 К),

Vcp Ут> ^{а ?}ср

Зависимость q_Cf> = /((7_ср) имеет Л/-форму и в диапазоне значений £₀ от £/3 до

Е на этой зависимости имеется падающий участок, т

Кривая ц/_ср = /(С/_о) интересна тем, что при относительно малых значениях £₀ по­токосцепление \р_ср>0, а при больших £₀ ч'_ср<0 При дальнейшем увеличении £₀ (при Eq > 1,5 В) 'Vcp снова становится положительным.

На зависимости ц/_ср - f (Eq) в той же области значений £₀ также имеется падаю­щий участок.

Так как в схеме рис. 15.54, а есть нелинейный конденсатор НК, то среднее значение тока за период Т_ск равно нулю. Период Т_ск зависит от величины £₀ (см. рис. 15.55, в). При плавном увеличении £₀ он то увеличивается, то уменьшается.

Каждое очередное изменение периода вызвано невозможностью сохранять смену со­стояний, которая характерна при меньшем значении Е_о. Первое увеличение период от 6 т до 8 т происходит при Eq -0,2 В. Из сопоставления рис. 15.55, а я б видно, что при Eq <10,2 В во второй отрицательный полупериод заряд НК успевает измениться до значе­ния ~q_m, Благодаря этому в третий отрицательный полупериод НК оказывается подго­товленным к принятию на себя отрицательного напряжения -£+ £₀. Если же £₀ будет больше 0,2 В, например 0.3 (см. рис. 15,55. б), то к концу второго отрицательного полу- периода заряд q не успевает достичь значения -q_m, и потому НК оказывается не подго­товленным к принятию на себя отрицательного напряжения в третий отрицательный полупериод. Это и вызывает затягивание процесса.

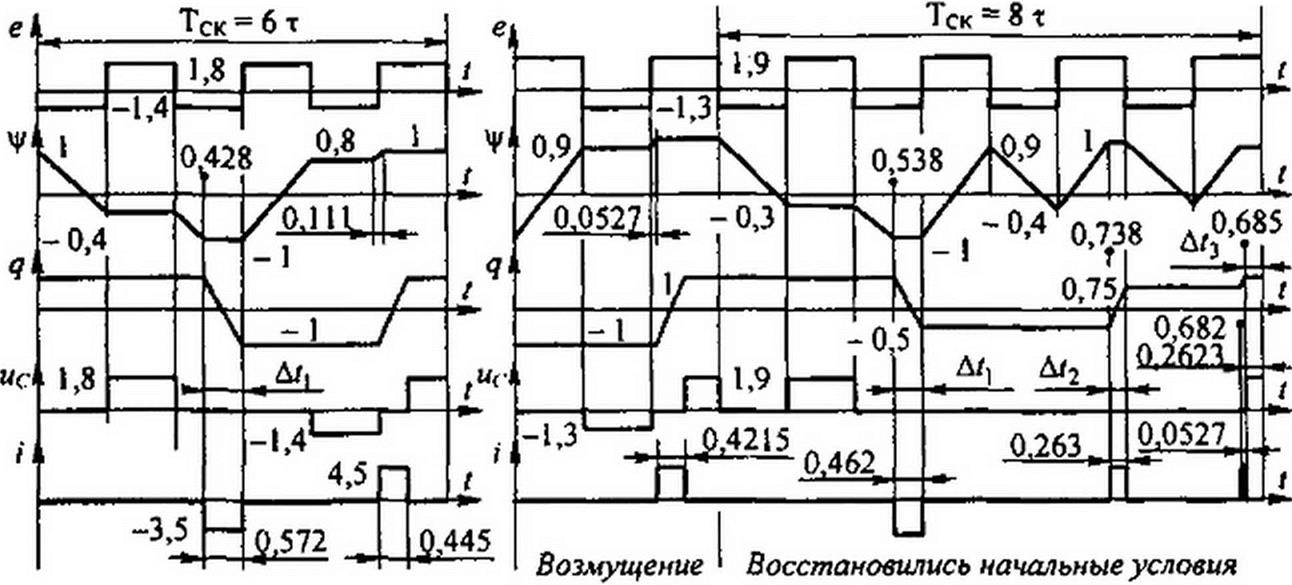
в

Рис. 15.55 (начало)

На рис. 15.55, а показан режим непосредственно до перехода от Г_ск = 61 к Г_ск = 8 -г.

Для аналитического определения значения Е_о, при котором происходит первое изме­нение периода (с 6 т до 8 т), учтем, что за время (2 т - Д/|) в два первых отрицатель­ных лолупериода (см. рис. 15.55, а) потокосцепление изменяется на 2ц/_т, а за время Д/, заряд изменяется на 2 q„,.

Следовательно, д,₌2т--^- и —^-A/,=2^.

£-£₀ R ^{1 Чт}

Отсюда

£₀ = E-y_mlx-q_m Rix.

Второе изменение периода (с 8 т до 6т) происходит при £₀ = 2 /х - £ = 0,4 В. Объясняется это тем, что во второй положительный полупериод (см. рис. 15.55, б) за вре­мя т потокосцепление изменяется на

2y„, =(£ + £₀)т.

Отсюда

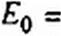
Третье изменение периода (с 6 т до 4т) происходит при Е_о = Е/3. Это соотноше­ние получаем, исходя из того, что всплески токов на рис. 15.55, г имеют место только за время Д/| и Д/₂. Изменения заряда по абсолютной величине равны, поэтому

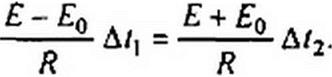Здесь

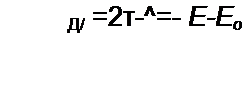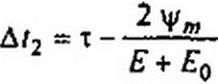Увеличение периода с 4 т до 8 т имеет место при Е_о - 0,6 В. Это увеличение обус­ловлено тем, что за два отрицательных полупериода вольт-секундная площадь (Е-Е₀)2т равна 2 ц/_л.

„ 2

Последующие изменения периода происходят при Е₀ = Е/2, Е_о = Е----------------------------------------------------------------

F — Р I ^т Р — Р У*” _н -г п

- t - —------- , Cq = h - —------------ и T. Д.

Таким образом, при плавном увеличении Е_о период субгармонических колебаний меняется скачками, а сами колебания становятся то четного, то нечетного порядка.

За исключением области значений Е_о от Е/3 до Е-ц/^/т, колебания при взятых сочетаниях параметров оказываются устойчивыми. Можно взять начальные условия

существенно отличающимися от тех, которые должны быть к началу установившегося ре­жима, и через некоторое относительно небольшое время режим становится таким, каким он был до получения возмущения. Процесс возвращения к установившемуся режиму ил­люстрируется левой частью рис. 15.55,6.

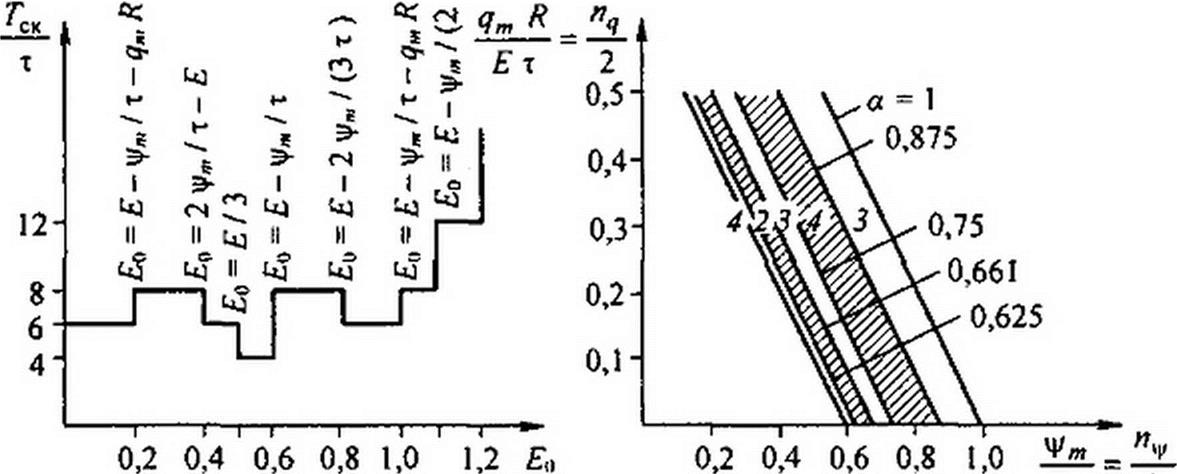
Воспользуемся рис. 15.56, а, б, в, кривыми рис. 15.55 а-ж и соотношениями, связы­вающими E_q, Е, ц/_т/т Е и q_mR!xE в каждом интервале изменения £₀ на рис. 15.55, для построения областей возможных типов движений в схеме рис. 15.54, а, изображен­ных на рис. 15.56, г. При п_(/12 > 0,5 (рис. 15.56, г) субгармонические колебания (СК) от­сутствуют. Наклонные прямые, отделяющие соседние области, построены по уравнению

y_mIEx + q_mRJEx = a или /2 + /2 = а.

Цифры на рис. 15.56, г указывают порядок возникающих СК. Область, заключенная между прямыми а-\ и а = 0,875, соответствует СК третьего порядка; между прямыми а - 0,875 и а = 0,75 — СК четвертого порядка и т.д.

При определении граничных значений а исходим из того, что для рассматриваемых на рис. 15.55 типов движений изменение заряда нелинейной емкости только в предельном случае может достигать значения 2q_m. Граничное значение а = 1 следует из условия су­ществования СК, рассмотренных в начале § 15.72. Значение а = 0,875 соответствует скач­кообразному изменению 7'_ск/т на рис. 15.56, «при £₀=0,2, когда при £ = 1,6 постоян­ная ЭДС £₀ = £-/т - q_m R/x. Отсюда

\1)_т /х Е + R q„ /х Е = 1 - Е_о/£ = 0,875.

Граница перехода от СК четвертого порядка к СК третьего порядка (£₀ = 0,4, а ~ 0,75) определена с учетом того, что за время т + х под действием напряжения £ - £₀ потоко­сцепление уменьшается со значения +ц/_т до значения -ц/_т.

Отсюда

_т_ ,_т
Е-£_о

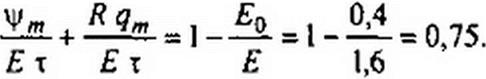За время т + х заряд в пределе может измениться на величину 2 q_m при протекании через нелинейный конденсатор тока ———, т. е.

Поэтому

В интервале значений Е_о от Е/3 до Е--^²- режим работы цепи неустойчив — ра­бочая точка находится на падающих участках кривых q_cp = f(U_cp) и м>_ср = Л^_ср)- Вме- сто СК второго порядка в цепи возникает хаос. В макросмысле рабочая точка при хаосе будет перемещаться по штриховой линии на рис. 15.56, а.

§ 15.72. Автомодуляция. Хаотические колебания (странные ат­тракторы). Автомодуляцией называют режим работы нелинейной элек­трической цепи, находящейся под воздействием периодической вынуж­дающей силы частотой о), при которой амплитуды токов и напряжений в цепи периодически изменяются без воздействия внешнего модулирую­щего фактора. Автомодуляция возникает вследствие неустойчивости пе­риодического режима работы на частоте вынуждающей силы <о. Процесс оказывается почти периодическим для огибающих амплитуд первых гар­моник и непериодическим (хаотическим) для мгновенных значений.

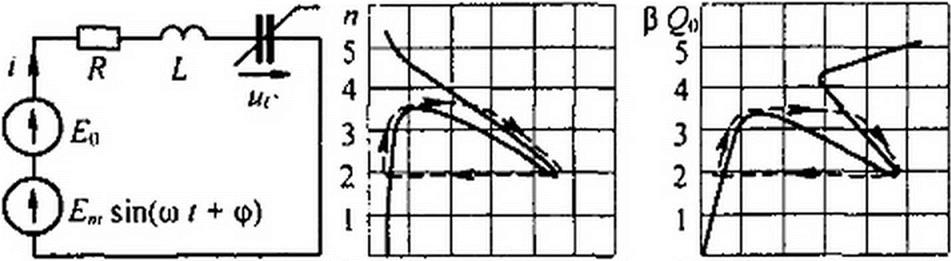
Выведем основные зависимости, описывающие процесс автомодуля­ции в схеме (на рис. 15.57, а) с нелинейным конденсатором, кулон-воль- тную характеристику которого в соответствии с § 15.26 выразим в виде и_с - a sh р q.

Так как в цепи действуют постоянная Е и синусоидальная Е_т sin(co t + q>) ЭДС, то заряд q имеет постоянную и синусоидальную компоненты:

Постоянная составляющая напряжения на конденсаторе (см. § 15.16)

L/_co =ashp0_o J_o (у 0&).

Первая гармоника и_С{ = 2 a ch 0 Q_o (-у J_l (J 0 Q_ni)) sin co /, первая гар­моника тока /]=(!) Q_nl cosco Л Если в уравнение цепи

di dt

подставить записанные выражения для U_CQ +и_с и разбить его в со­ответствии с методом гармонического баланса на уравнения для посто­янной составляющей, а также для синусной и косинусной компонент, а затем два последних уравнения возвести в квадрат и сложить для устра- 0 Е „

нения угла ф, то, введя обозначения а = —д , 6 =------------------------------------------------------------- , 0£)_о=л,

со L (a L

$Qm ~^т> получим два следующих уравнения:

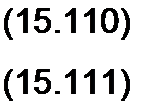ash и J_Q (у w) = E_q = U

b² т² + (с (-у (у т) ch п - w))² = а².

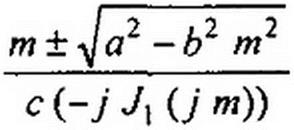
Решим (15.111) относительно ch«:

(15.112)

Уравнение (15.112) дает связь между п и w, обусловленную парамет­рами цепи по первой гармонике частоты со, а уравнение (15.110)— по постоянной составляющей. На рис. 15.57, б изображена зависимость п от т, построенная по соотношению (15.112) при а = 0,5; b = 0,1; с = 0,054. Верхний участок кривой соответствует знаку плюс, а нижний — знаку минус перед радикалом в формуле (15.112).

Задаваясь значениями п в интервале 0-^6 и беря соответствующие им значения т из рис. 15.57, б, по формуле (15.110) строим зависимость 02о = (рис. 15.57, в). Из рисунка видно, что в области значе­

ний С/_со/а = 35-4-60 имеется падающий участок, не прикрытый восхо­дящими участками.

Из рис. 15.57, в видно, что дифференциальная емкость нелинейного конденсатора по приращениям постоянных Составляющих заряда Д0_О и напряжения ДС/_с0 на падающем участке зависимости 0 Qq = /(</_{< 0})

отрицательна: С_д0 =---------- $-<0. В соответствии с § 17.2, исследуем,

устойчиво ли будет положение изображающей точки, если она окажется на падающем участке этой зависимости, не прикрытом восходящими ветвями. В исходном положении U_CQ = Е и среднее за период Т~ 1 / f значение среднего тока /_ср = 0. Положим, что £/_со получило малое при­ращение ДС/( о > 0 флюктуационного происхождения. Ему будет соответ­ствовать отрицательное приращение заряда Д0_ГО = C_d0 ^и отрица-

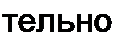приращение среднего за период тока в цепи

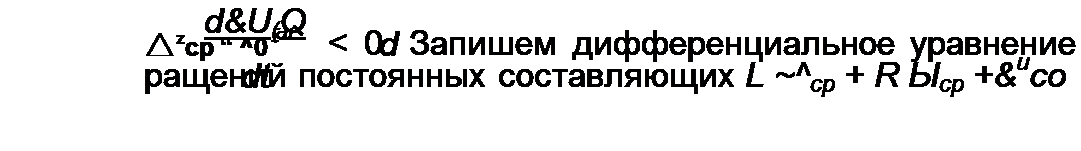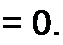После алгебраизации ему соответствует характеристическое уравне­ние

L Qo р¹ + R Qj Р +1 - 0’

Один из двух корней его положителен (т. к. C_rt0 < 0) что свидетельствует о неустойчивости положения рабочей точки на па­дающем участке на рис. 15.57, в. Изображающая точка на этом рисунке будет двигаться по штриховой линии. Движение по штриховой линии описывает макропроцесс в схеме. Для мгновенных значений тока, заряда, напряжений на элементах схемы процесс будет являться непери­одическим. Такого рода непериодические процессы в нелинейных элек­трических цепях переменного тока, причины возникновения которых представляются непонятными, в зависимости от степени их упорядочен­ности, условимся называть автомодуляцией, или хаосом. Если высшие гармоники в этих процессах в токах и напряжениях будут выражены сла­бо, то такие процессы будем именовать автомодуляцией, если сильно — хаосом. Автомодуляцию и хаос можно рассматривать как катастрофу ожи­даемого периодического режима. В иностранной литературе последних лет подобные колебания стали называть странными аттракторами (атт­рактор — это путь от одного типа движения к другому’*), самим назва­нием подчеркивая, что природа его непонятна.

Основная причина возникновения такого рода процессов — проявле­ние ряда малоизвестных физических явлений, приводящих к возникно­вению нелинейной неявно выраженной обратной связи, осуществляемой в той или иной схеме, чаще всего через взаимодействие гармоник раз­ных частот. При возникновении обратной связи через нелинейное взаи-

*’Термин «странные аттракторы» предложен в 1971 г. Руэлем и Тиксеном в работе, посвященной турбулентным движениям в вязкой несжимаемой жидкости при большом числе Рейнольдса.

модействие гармоник тока (напряжения) различных частот входная цепь (для протекания тока одной частоты) и выходная цепь (для протекания тока другой частоты) могут быть либо совмещены» либо быть раздель­ными. Выявлению каналов действия такой обратной связи в схемах с различными управляемыми и неуправляемыми нелинейными элемента­ми посвящено Приложение П10. В нем показано также» в чем отличие этих колебаний от автоколебаний в цепях с постоянными во времени источниками ЭДС или тока.

§ 15.73 Конвергентные и неконвергентные электрические цепи. Познакомимся с понятиями конвергентная и неконвергентная электри­ческая цепь, используемыми в литературе. Под конвергентной будем по­нимать цепь, в которой при любых значениях ее элементов, любых на­чальных условиях и любых периодических источниках питания устанав­ливается единственно возможный вынужденный режим работы, период которого равен периоду источника питания. Если же в цепи при некото­рых значениях ее элементов возможно существование нескольких различ­ных вынужденных режимов при одном и том же значении входного на­пряжения или тока, либо в цепи возникает нежелательный режим рабо­ты, период которого не равен периоду источника питания схемы, или в цепи возникает хаос или автомодуляция, то такая цепь неконвергентна.

Все линейные электрические цепи с неизменными во времени пара­метрами конвергентны. Однако некоторые нелинейные электрические цепи с периодическими источниками при определенных значениях пара­метров могут оказаться неконвергентными (примеры см. в § 15.58, 15.60, 15.69, 15.70 и в Приложении П10).

Неконвергентными при определенных значениях параметров могут оказаться и нелинейные цепи, содержащие постоянные во времени источники ЭДС или тока. К их числу могут быть отнесены некоторые автоколебательные системы, а также цепи, содержащие нелинейные резистивные элементы, вольт-амперные характеристики которых имеют S'- или /V-образную форму. В ряде автоколебательных систем неконвер- гентность приводит к тому, что вместо ожидаемого периодического ре­жима работы в схеме возникают перерывы в работе, биения, автомоду­ляция или хаос. В системах, содержащих нелинейные элементы с S- или jV-образными вольт-амперными характеристиками, установившийся ре­жим работы схемы может оказаться зависящим от предыстории.

§ 15.74 Дуальные нелинейные цепи переменного тока. Две нели­нейные электрические цепи (схемы) переменного тока условимся назы­вать дуальными, если:

1) каждому независимому контуру исходной схемы, а также области, являющейся внешней по отношению к схеме, соответствует узел в ду­альной;

2) независимые контуры составлены так, что каждая ветвь исходной схемы, содержащая нелинейный элемент, входит только в один незави­симый контур (не входит в соседние) и является периферийной (пункт 2
в общем случае необязателен, он имеет существенное значение при рас­чете цепей, если его предполагается провести);

3) образование ветвей дуальной схемы между ее узлами производит­ся так же, как и для линейных цепей (§ 3.44-3.45) — каждому элементу исходной схемы соответствует своя ветвь в дуальной;

4) заполнение ветвей дуальной схемы схемными элементами, дуаль­ными элементам исходной, осуществляется по тому же принцип)', что и в линейном случае с одинаковым масштабным множителем для линей­ных и нелинейных элементов.

Если это будет выполнено, то физические процессы, происходящие в исходной схеме по отношению к напряжениям на ее элементах, будут с точностью до масштабного множителя сопровождаться аналогичными процессами по отношению к токам в соответствующих ветвях дуальной схемы.

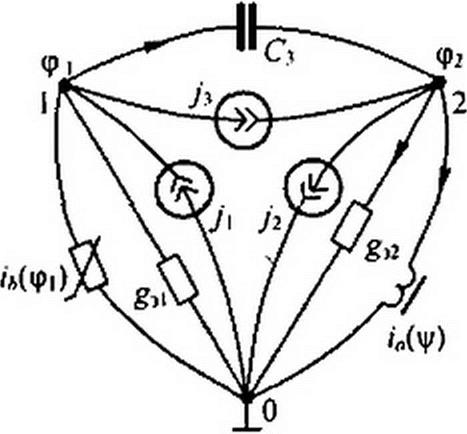
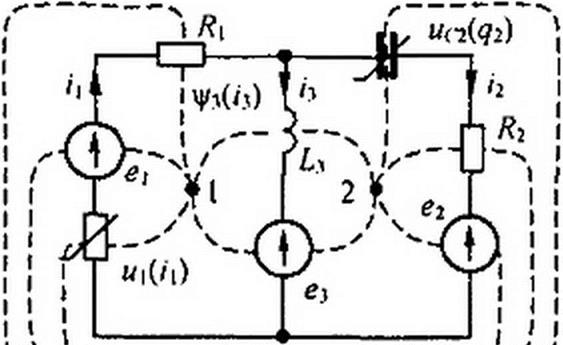
В качестве примера на рис. 15.58, а изображена исходная схема. В ней три ветви и два независимых контура. Она содержит два линейных резистора— Я₍ и /?₂, нелинейное резистивное сопротивление М|(/₍),ли-

Рис. 15.58

нейную индуктивность и нелинейный конденсатор с вольт-кулоновой характеристикой «02(^2). Для образования дуальной схемы в каждом независимом контуре исходной схемы ставим по точке, обозначив их циф­рами / и 2. Во внешней по отношению к схеме области исходной схемы ставим точку и обозначаем ее 0. Эти точки будут узлами дуальной схе­мы, изображенной на рис. 15.58, б. Точки I и 0 на рис. 15.58, а соединя­ем тремя штриховыми линиями, проведенными через элементы первой ветви, и в дуальной схеме на рис. 15.58, б в эти ветви включаем источ­ник тока j_}, нелинейную проводимость /^(<pj) и линейную проводимость g₃₁ дуальные элементам первой ветви. Точки / и 2 на рис. 15.58, а со­единяем двумя штриховыми линиями и на рис. 15.58, б в соответствую­щие им ветви включаем линейный конденсатор С₃ и источник тока у₃. Точку 2 на рис. 15.58, а соединяем с точкой 0 тремя штриховыми линия­ми, проходящими через резистор /?₂, нелинейный конденсатор, вольт- кулоновая характеристика которого w_C2(^2)’ ^и источник ЭДС е₂-

В дуальной схеме между узлами 2 и 0 включены, соответственно, нели­нейная индуктивность, вебер-амперная характеристика которой /_а(ф), ли­нейная проводимость #32 ^и источник тока у₂. Если направление обхо­да к контура совпадает с направлением стрелки на источнике ЭДС е_т, то в дуальной схеме ток источника тока должен быть направлен к А-узлу, если не совпадает, то от к -узла. Чтобы выявить соответствие между эле­ментами исходной схемы и элементами дуальной, составим уравнения по второму закону Кирхгофа для исходной схемы на рис. 15.58, а (см. урав­нения (15.113) и (15.114)) и уравнения по первому закону Кирхгофа для дуальной схемы на рис. 15.58, 6 (см. уравнения (15.115) и (15.116)) и за­тем сопоставим их:

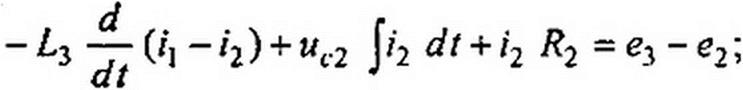
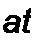
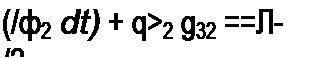(15.113)

(15.114)

(15.115)

(15.116)

При составлении уравнений (15.113) и (15.114) учтено, что /₃ = i_} -i₂ и что заряд q₂ -jt'2 dt. При составлении уравнений (15.115) и (15.116) учтено, что напряжение на линейном конденсаторе С₃ равно ср] -<р₂, а потокосцепление ф нелинейной индуктивности в схеме на рис. 15.58, б равно |<р₂ поскольку потенциал точки 0 принят равным нулю.

Для того чтобы потенциал точки /, т. е. ф₁₅ изменялся во времени так же, как ток а потенциал точки 2, т. е. ф₂, как /₂, отношение анало­гичных слагаемых в уравнениях (15.113) и (15.115) должно быть одина­ково и равно произвольно выбранному масштабному числу т (Ом):

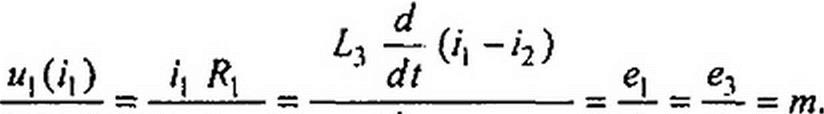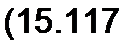Отношение аналогичных слагаемых в уравнениях (15.114) и (15.116) так­же равно т:

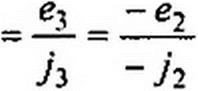
dt ^0| Ц(-2 (рз _ i₂ R₂

-С₃—(ф]-ф₂) АД/фг^') Фг£э1

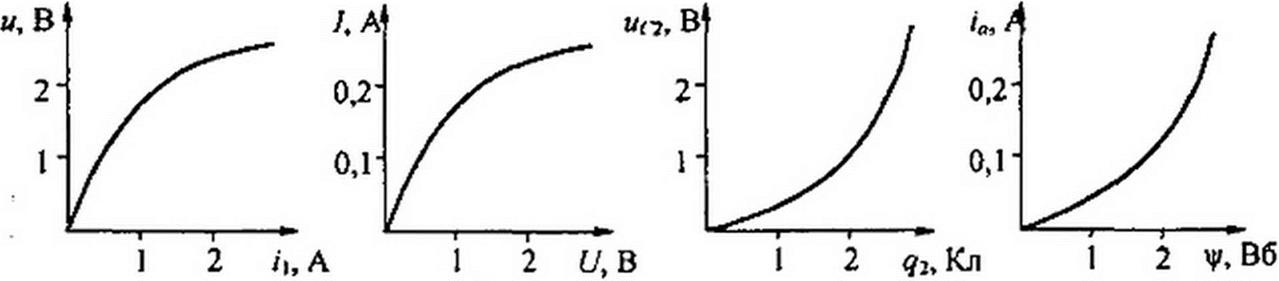
Из (15.117) следует, что ВАХ нелинейного резистора исходной схе­мы W](/|) и АВХ нелинейной проводимости дуальной схемы /Дф,) свя­заны соотношением w_I(fj) = т i_e (<р,), причем ординаты АВХ /_в(ф])

уменьшены в т раз по сравнению с ординатами ВАХ Uj(7|). Так, если ВАХ исходной схемы соответствует рис. 15.59, а, то АВХ дуаль­ной схемы соответствует рис. 15.59, б (т взято равным 10).

Из (15.118) следует, что вольт-кулоновая характеристика и_С2(Я2) нелинейного конденсатора исходной схемы связана с ампервеберной характеристикой /_о(\р) нелинейной индуктивности зависимостью ^ис2 (*72) ~^т i_a (Ч>) (^см- Р^ис- 15.59, в и г).

Вопросы для самопроверки

1. Охарактеризуйте известные вам типы нелинейных резистивных, индуктивных и емкостных элементов. 2. Как понять выражение «нелинейные элементы являются генера­торами высших гармоник тока (напряжения)»? 3. Какие преобразования можно осуще­ствить с помощью нелинейных электрических цепей? 4. Какие физические явления могут наблюдаться в нелинейных и не могут в линейных цепях с постоянными параметрами? 5. Как из характеристик для мгновенных значений можно получить ВАХ для первых гар­моник и ВАХ для действующих значений величин? 6. Проанализируйте зависимость ин­дуктивного сопротивления для нелинейной индуктивной катушки от амплитуды приложен­ного напряжения при неизменной частоте со. 7. Качественно начертите семейство ВАХ уп­равляемой индуктивности и управляемого нелинейного конденсатора и сопоставьте их. 8. Чем объяснить, что ВАХ управляемой нелинейной индуктивности (см. рис. 15.15,6) имеют насыщение по напряжению, а ВАХ управляемого нелинейного конденсатора (см. рис. 15.15, в) — по току? 9. Чем можно объяснить, что постоянная составляющая заряда Qo на нелинейном конденсаторе зависит от амплитуды Q_m первой гармоники заряда? 10. Начертите схемы замещения электронной лампы и биполярного и полевого транзис­торов для малых переменных составляющих. 11. Охарактеризуйте основные положения известных вам методов расчета периодических процессов нелинейных цепей. 12. Сфор­мулируйте условия нахождения моментов времени открытия и закрытия диодов. 13. По­кажите, что для перемагничивания сердечника нелинейной индуктивности от до +V_W под действием напряжения и(О необходимо выполнить условие 2 = £’«(/)<//,

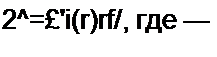а для перезарядки нелинейного конденсатора от -q„, до под действием протекаю­щего через него тока /(/) необходимо выполнить условие амплитуда потокосцепления; q„ —заряд; —время перемагничивания (перезарядки).

14. Что понимают под автоколебаниями? Как выявить условия, когда они возникают?

15. В чем причина возникновения субгармонических колебаний? 16. В чем причина воз­никновения автомодуляции? 17. В чем отличие субгармонических колебаний от автомо- дуляционных? 18. В чем принципиальное отличие феррорезонанса напряжений и токов от соответствующих резонансов в линейных цепях? 19. При каких условиях в электричес­ких цепях могут возникать триггерные явления? 20. Возможны ли триггерные явления в схеме (см. рис. 15.43, а), если источником питания схемы будет не источник ЭДС, а источник тока? 21, Можно ли ожидать возникновения триггерных явлений в схеме

(см. рис. 15.45, а), если на входе ее будет источник ЭДС? 22. Что понимают под частот­ными характеристиками нелинейных цепей? 23. Чем принципиально отличаются частот­ные характеристики нелинейных цепей от частотных характеристик аналогичных линей­ных? 24. В чем сходство и в чем различие в построении векторных диаграмм по первым гармоникам для линейных и нелинейных цепей? 25. Дайте определение понятий «индук­тивность рассеяния», «намагничивающий ток», «ток потерь». 26. Постройте векторную диаграмму трансформатора со стальным сердечником при активно-емкостной нагрузке. 27. Составьте алгоритм расчета нелинейной цепи с учетом первой и одной из высших гар­моник. 28. К нелинейному резистору с симметричной характеристикой приложено перио­дическое напряжение без постоянной составляющей. Можно ли утверждать, что протека­ющий через него ток не может содержать постоянную составляющую? 29. Электрическая цепь без потерь состоит из последовательно соединенных линейной индуктивности L и нелинейного конденсатора, кулон-вольтная характеристика которого описана выражением и_с -ashbq. Вывести формулу для угловой частоты свободных колебаний о₀ в цепи,

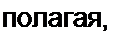
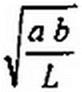
что при t = 0 ток i - 0, а заряд q равен ^(0). {Ответ-. 4 к(о>

, где К — эллиптический интеграл первого рода.) 30. Решите

задачи 10.9; 10.10; 10.20; 10.23; 10.37; 10.38; 10.39; 10.41; 10.48; 10.58; 10.61.

Глава шестнадцатая

ПЕРЕХОДНЫЕ ПРОЦЕССЫ

•В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

§ 16.1 Общая характеристика методов анализа и расчета переход­ных процессов. Методы анализа и расчета переходных процессов в нелинейных цепях могут быть классифицированы:

а) по виду основных операций, которые необходимо выполнять для интегрирования нелинейных дифференциальных уравнений, — на гра­фические (графоаналитические) и аналитические;

б) по характеру величины, для которой производится расчет (по мгно­венным значениям токов и напряжений), по мгновенным значениям оги­бающих токов и напряжений (их первых гармоник) либо по мгновенным значениям медленно меняющихся средних за период внешнего воздей­ствия значений.

Под графическими {графоаналитическими} понимают такие методы, в которых основными операциями при определении зависимости от вре­мени искомых токов и напряжений являются графические построения, нередко сопровождаемые и некоторыми вспомогательными числовыми подсчетами.

В графических методах характеристики нелинейных элементов обыч­но не требуется выражать аналитически (см. § 16.2 и 16.3).

Аналитическими называют такие методы, в которых основной опера­цией при определении зависимости искомых токов и напряжений от вре­мени является точное (приближенное) интегрирование дифференциаль­ных уравнений цепи, с использованием аналитических выражений харак­теристик нелинейных элементов.

Рассмотрены следующие аналитические методы:

1) метод интегрируемой нелинейной аппроксимации (см. § 16.3);

2) метод кусочно-линейной аппроксимации (см. § 16.4);

3) метод медленно меняющихся амплитуд (см. § 16.6);

4) метод малого параметра (см. § 16.7);

5) метод интегральных уравнений (см. § 16.8).

Графические методы (§ 16.2 и 16.3) имеют следующие преимущества перед аналитическими:

а) нет необходимости выражать характеристики нелинейных элемен­тов аналитически, что позволяет избавиться от погрешностей, связанных с аналитическим представлением характеристик;

б) простота учета гистерезиса и других сложных нелинейных зависи­мостей.

В свою очередь, аналитические методы также имеют перед графиче­скими преимущества. Из них основным является то, что они дают воз­можность получить решение в общем виде, а не для какого-то одного конкретного сочетания параметров. Получить решение в общем виде
желательно потому, что анализ его позволяет выяснить все особенности процесса при изменении всех параметров.

Как упоминалось, все методы расчета могут быть подразделены на две подгруппы:

1 ) расчет по мгновенным значениям токов и напряжений;

2 ) расчет по мгновенным значениям огибающих токов и напряжений.

Расчет по огибающим важен тем, что он дает возможность, не вдава­ясь в мелкие детали процесса внутри каждого периода действующей в схеме периодической ЭДС (внутри каждого периода автоколебаний в ав­токолебательной системе), судить о макроструктуре процесса. Он возмо­жен не только для нелинейных цепей, он представляет существенный интерес и для линейных цепей.

Точность расчета по огибающим уступает точности расчета по мгно­венным значениям. Однако возможность судить о макроструктуре про­цесса часто является решающим фактором.

Там, где это необходимо, целесообразно дополнять расчет по огибаю­щим расчетам по мгновенным значениям. Метод расчета по огибающим представлен методом медленно меняющихся амплитуд (см. § 16.7 и 16.13). Остальные методы относятся к подгруппе расчета по мгновен­ным значениям.

Теория переходных процессов в электрических цепях с управляемы­ми нелинейными индуктивными, емкостными и резистивными элемен­тами, а также в электромеханических системах и цепях с управляемыми источниками с учетом их нелинейных и частотных свойств рассмотрена в § 16.9-16.13.

3 16.2. Графический метод, основанный на разделении перемен­ных. Метод применим к нелинейным электрическим цепям, описывае­мым дифференциальными уравнениями первого порядка, допускающим разделение переменных. Последняя оговорка свидетельствует о том, что метод применим к цепям постоянного и, как правило, неприменим к це­пям переменного тока. Основные этапы и последовательность расчета проиллюстрируем на примере.

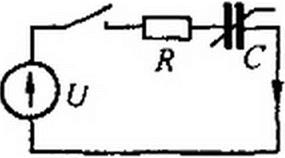
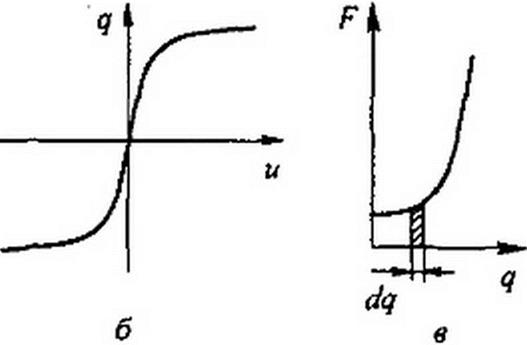
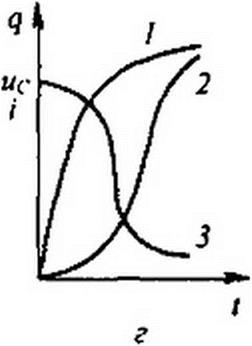
Нелинейный конденсатор через резистор подключается к источнику ЭДС Е (рис. 16.1, о). Кулон-вольтная характеристика (КВХ) конденсатора задана графически (рис. 16.1,6). Полагая, что в схеме нулевые начальные условия, построить кривые изме­нения заряда q, напряжения на конденсаторе и_с и тока i в функции времени. Составим дифференциальное уравнение:

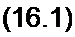⁺ * ^-=Е.
al

Разделим переменные;

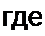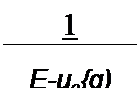Для построения кривой F(q) используем КВХ (рис. 16.1, в).

Левую часть уравнения (16.1, а) проинтегрируем по / от 0 до текущего значения t, а правую — по q от q = 0 до текущею значения q. В результате получим

ч

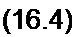t~R ^F(q)dq.
о

Графически подынтегральное выражение F(q)dq представляет собой заштрихован­ную площадку (рис. 16.1, в).

Кривая / на рис. 16.1, г качественно представляет собой зависимость q от t. С помо­щью кривой q = /(/) и КВХ нелинейного конденсатора строят зависимость ис{() (кривая 2). Ток в цепи для произвольного момента времени определяется по формуле i -((/ - u_c)f R (кривая 3).

4 16.3. Метод, основанный на подсчете определенного интеграла по формуле трапеций. Если интервал интегрирования b-а в опреде- ь

ленном интеграле Jy(x) dx разбить на п равных частей и обозначить а

значения функции у(х) через Уо,У},у₂,--- ^ПР^{И х}о ~ + х₂ = а + 2 h... соответственно, где h = (b-a)/n, то

/> t) а

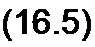Jy(x) dx = —- (y₀ + 2 у, + 2 у₂ +... 2 у„_, + у_п).

Г 2 п

Рассмотрим идею метода (предложена в 1916 г. русским инженером В, Волынкиным) на примере цепи, приведенной на рис. 16.2, а. Цепь содержит источник ЭД С е(г), нелинейную индуктивность, резистор R. Зависимость потокосцепления ц/(/) нелинейной индуктивности задана графически — кривая на рис. 16.2, 6, начальные условия полагаем нуле­выми, т. е. /(0) = 0, ц/(0) = 0. Составим уравнение

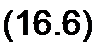с/\|/ / dt + Ri = е(/).

Разделим текущее время t на равные промежутки т (/ = п т), тогда вме­сто (Ь-а)(2п в(16.5)будем иметь (л т-0)/2 п = т/2. Последователь­но проинтегрируем уравнение (16.6) сначала от t = 0 до t = т, затем от г = 0 до / = 2т ит.д., каждый раз используя формулу трапеций. Для первого интервала

t < с _т

+ R р dt » je(/) dt; fydt = — i\,
оо о

Следовательно,

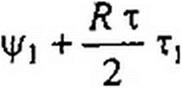Для ^ = 2т

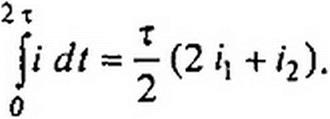Поэтому для t - 2 т

2т

р(/) dt-Rx /|.

о

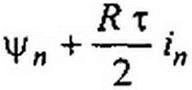
При t = nx

(16.7)

Формула (16.7) позволяет последовательно определить

В ее левую часть входят неизвестный ток i_n и соответствующее ему W-1

потокосцепление \р_л, а значение в правой части известно по к «1

результатам расчета за предыдущие интервалы времени.

Последовательность расчета следующая: Л т

1) по заданной е(/) подсчитываем значения функции je(/) dt для раз­личных п; ⁰

2) на рис. 16.2, б проводим прямую OS под углом а к оси абсцисс, R т т,

тангенс которого равен-------------- где m_t и т — масштабы по осям /

. 2 т,.,

и 4; ^v

3) значения тока и потокосцепления j к конц}/ первого интерва­ла времени определим исходя из (16.7) по величине je(t)df. Эта вели- о

чина в масштабе потокосцепления должна быть равна отрезку BD на рис. 16.2, б. Отрезок ВС будет равен а отрезок CD — значению

/р Ток /| равен отрезку ОС\

4) ток /₂ ^к концу второго интервала времени и значение ц/₂ находим аналогично: по (16.7) подсчитываем правую часть (она теперь равна

е(/) di - R т /0 и перемещаем отрезок, равный правой части, параллель- о

но оси ординат так, чтобы один его конец оказался на кривой \|/(/)> а другой — на прямой OS. Далее определяем значения /₃ и у₃ к концу

третьего интервала, когда правая часть (16.7) равна |е(г) dt -Rx (i_{ + i₂) и т. д. ⁰

Применим рассматриваемый метод к расчету переходного процесса в цепи, приведенной на рис. 16.2, в, при нулевых начальных условиях /(0) = ц/(0) = 0. К источнику ЭДС е(г) подключается цепь, состоящая из нелинейной индуктивности с известной ц/(/), и нелинейный резистор, ВАХ z/(z) которого изображена на рис. 16.2, г. Уравнение цепи

—— + u(i) = е(/) проинтегрируем по t от 0 до / = п т. Учтем, что at

п т

Jw(O dt = у (2 «(/)) + 2 u(i₂) +... + 2 у(/„_]) + w(z„)) о ²

и получим формулу, аналогичную (16.7):

л-1

V«⁺“«0„)= \e(l)dt-x 2>(z*). (16.8)

² о *=i

Последовательность расчета по формуле (16.8) такая же, как и по

(16.7), с тем отличием, что вместо прямой — R i {OS на рис. 16.2, б) на 2

х рис. 16.2, д надо нанести кривую — u(i).

Применение метода к цепи второго порядка с тремя разнохарактер­ными нелинейными элементами рассмотрено в [24].

§ 16.4. Расчет методом интегрируемой нелинейной аппроксима­ции. Данный метод основан на аппроксимации характеристики нелиней­ного элемента такой нелинейной функцией, которая, во-первых, дос­таточно точно отображает его характеристику в предполагаемом интер­вале перемещения изображающей точки по ней и, во-вторых (и это главное), дает возможность точно проинтегрировать уравнение в извест­ных функциях.

Ценность метода заключается в том, что в результате интегрирования получают зависимость исследуемой величины от времени и всех пара­метров схемы.

Метод применим к дифференциальным уравнениям первого порядка» а также к уравнениям, сводящимся к уравнениям первого порядка путем замены переменных.

Пример 161. Определить закон нарастания во времени тока при замыкании ключа в схеме (рис. 16.2, а). Зависимость тока от потокосцепления V выражена формулой / = к ц/⁴. В схеме нулевые начальные условия.

б/ Ф dw гч

Р е щ е н и е. Из уравнения цепи —— + Ri = U следует, что dt = ———. Вынесем из dt U - Ri

знаменателя множитель R и заменим i на к ц>⁴ :

¹ dt = — ——■—- у

R /_у - к ц/⁴

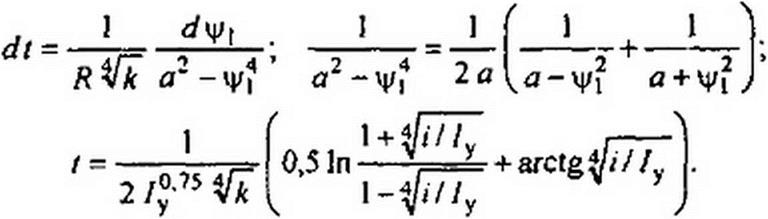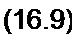§ 16.5 Расчет методом кусочно-линейной аппроксимации. При рас­чете этим методом осуществляется замена характеристики нелинейного элемента отрезками прямых линий, что позволяет перейти от нелиней­ного дифференциального уравнения к нескольким линейным уравнени­ям, отличающимся друг от друга лишь значениями коэффициентов.

Каждое из линейных уравнений справедливо для того интервала вре­мени, в течение которого рабочая точка перемещается по соответствую­щему линеаризованному участку. Метод применим к цепям, содержащим источники постоянной и (или) синусоидальной ЭДС, а также к цепям первого и более высоких порядков.

Для сложных нелинейных цепей с источником (источниками) сину­соидальной ЭДС основная трудность расчета данным методом заключа­ется в определении постоянных интегрирования, исходя из законов ком­мутации и времени работы на каждом линейном участке. В сложных цепях неизвестные находят обычно из трансцендентных уравнений, час­то применяют ЭВМ. Впервые идея этого метода была высказана россий­ским физиком Н.Д. Папалекси в 1912 г.

Рассмотрим основные этапы расчета на простейшем примере.

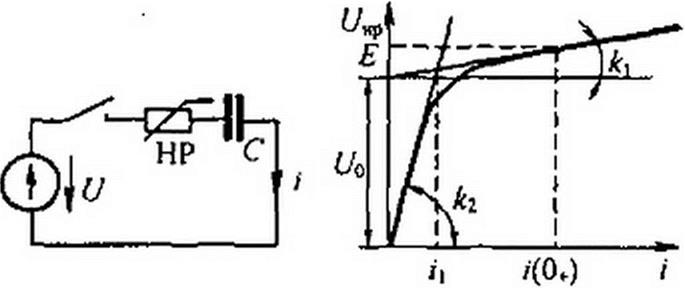
Пример 162. Конденсатор емкостью С заряжается через HP от источника постоянно­го напряжения U (рис. 16.3. а}. Определить закон изменения тока в цепи при зарядке.

Решение. ВАХ HP заменим двумя отрезками прямых линий (рис. 16.3, б). Пусть на участке от i = 0 ло i-i_} u_HJJ = А₂ /, где — напряжение на нелинейном резисто­ре; — коэффициент. На участке i > Ыцр ~ Uo ⁺ *■

Размерность коэффициентов к_} и к₂ соответствует размерности сопротивления. В уравнение цепи и₍- + а_НР = U вместо и₍- подставим заменим д_К1> для первого

участка на + к_{ i, а для второго — на к₂ I.

При зарядке конденсатора ток постепенно уменьшается от максимального значения до нуля. Поэтому изображающая точка перемешается сначала по первому участку, а затем по второму.

Для первого участка — р dt + (J_o + A, i = Е;

для второго — J i at + к₂ 1 - t.

Для первого участка i = /_пр + i_C9 - 0+ е"^//А* ⁶ .

Постоянную интегрирования найдем из начального условия: / = 0, «_с=0. Поэто­му Uq + к_} /(OJ = Е и /(0₊)= Л] =(£-t/₀)/Aj. Следовательно, при работе на первом уча­стке

(16.10)

Пусть при / -ток > = /_t. Подставим в (16.10) i\ вместо / и вместо / и решим полученное уравнение относительно z₍:

При работе на втором участке / = Л₂ е *^{2 (} , причем а₂ ~

§ 16.6 Расчет переходных процессов в нелинейных цепях методом переменных состояния на ЭВМ» Рассмотрим методику расчета, исполь­зуя понятия дифференциальной индуктивности индуктивной катушки

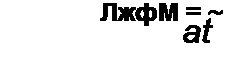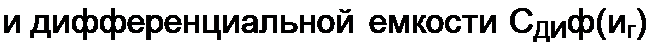го конденсатора.

Если вебер-амперная характеристика нелинейной индуктивности

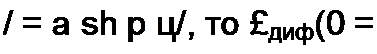Если кулон-вольтная характери­стика конденсатора и_с -a^ibq, то Сд_Нф(и_с) =

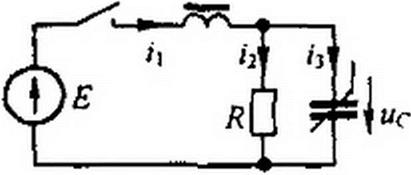
Пример 163. Составить систему уравнений по методу переменных состояния для схе­мы (рис. 16.4) при нулевых начальных условиях и указанных на рисунке положительных направлениях отсчетов токов и напряжений.

Решение. Из уравнения i_t = /₂ + /₃ следует u_c dq du_c u_c _ . .du_c ..

'i =-f⁺ w d ^+Сд"ф("с)-^Г- ^Из Уравнения

R aur at R at

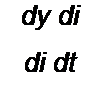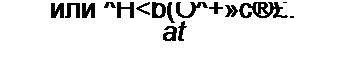---- + u_c = £ имеем dl

Искомая система уравнений:

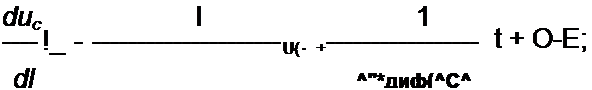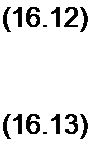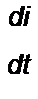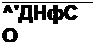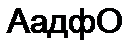Значения £_ДИф(0 и С_а1!ф(ы_г) на (£ +1)-шагс интегрирования подсчитывают по зна­чениям i и и_с на А-м шаге.

§ 16.7 Метод медленно меняющихся амплитуд. В электро- и радио­технике для расчета переходных процессов широко применяют метод медленно меняющихся амплитуд. Этот метод был предложен в 1921 г. голландским ученым Ван-дер-Полем.

Рассмотрим основы этого метода на примере нелинейной цели вто­рого порядка, находящейся под воздействием периодической возмуща­ющей силы.

Пусть уравнение этой цепи записано следующим образом:

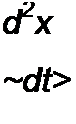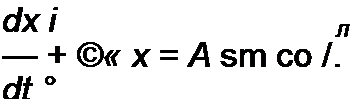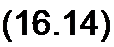Под действием периодической силы с частотой © в цепи устанавли­вается вынужденное колебание, первая гармоника которого имеет частоту со. Полагаем, что высшие гармоники выражены слабо.

Искомая функция х(/) может быть представлена как

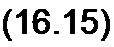х = a sin © t + b cos © г,

где а и b — медленно меняющиеся во времени амплитуды искомого ко­лебания.

Медленность изменения а и b во времени определяется тем, что их производные по времени являются величинами первого порядка малости по сравнению с произведениями © а и Ь©:

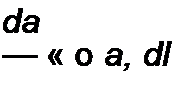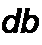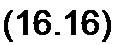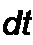Если это учесть, то, вместо того чтобы взять

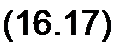dx ... da db

— = am cos © t - b о sm w t + sm © t — + cos © t —,
dl di dt

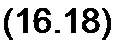можно в первом приближении принять

— « а (й cos t - b со sin co t. dt

Аналогично, вместо того чтобы вторую производную брать в виде

J

d x ? da . db

—-«-co a sin co /-co b cosco / + co cosco/---------------------------------------------------- co sin co / — +

Л² dt dt

d²a , d²b da . db

н---- г sin и t + —z- cosco / + +o) cosco t------ co sin co t —,

dt² dt² dt dt

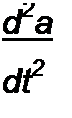
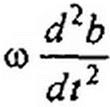
пренебрежем в ней слагаемыми второго порядка малости (учтем, что