Индуктивное сопротивление Хх - со Дл называют индуктивным сопротивлением рассеяния.
Схема замещения нелинейной индуктивности изображена на рис. 15.50, 6. Она отличается от схемы на рис. 15.3, а тем, что в ней добавлено сопротивление Хх. В неразветвленной части схемы включены резистивное сопротивление R обмотки w, и индуктивное сопротивление рассеяния Хх.
На участке cb есть две ветви. Правую ветвь образует идеализированная нелинейная индуктивность, по которой проходит намагничивающий ток Д. Левую ветвь образует активное сопротивление Яс, потери в котором равны потерям Рх на гистерезис и на вихревые токи в сердечнике нелинейной индуктивности. По левой ветви течет ток
(15.89)
На рис. 15.50, в изображена векторная диаграмма нелинейной индуктивности в соответствии со схемой на рис. 15.50,6. Эта векторная диаграмма строится так же, как и для обычных линейных схем.
Начнем ее построение с потока Ф„,.
Потоки ФР) и Ф¥ пронизывают обмотку Wj (см. рис. 15.50, а) и наводят в ней ЭДС самоиндукции.
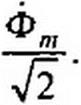
|
Напряжение (jah на зажимах идеализированной нелинейной индуктивности равно по величине и противоположно по знаку ЭДС самоиндукции, возникающей в обмотке w, схемы (рис. 15.50, а) под действием основного потока Фп|:
(15.90)
Деление на V2 объясняется переходом от амплитудного значения потока к действующему. Напряжение йсЬ на 90° опережает поток Ф .
Ток / — это ток через идеализированную нелинейную индуктивность, в сердечнике которой нет потерь энергии; он на 90° отстает от напряжения (jeb и по фазе совпадает с потоком Фи. Ток /с совпадает по фазе с напряжением (1сЬ. Определение токов и 1С рассмотрено в § 15.67 и 15.68.
По первому закону Кирхгофа,
/ = /и + Л- (15.91)
Напряжение (jab на входе схемы равно геометрической сумме напряжения йсЬ, падения напряжения / R в резистивном сопротивлении и падения напряжения j 1 Xs в индуктивном сопротивлении рассеяния.
Токи и 1С не пропорциональны напряжению U аЬх а следовательно, и напряжению Uab на входе схемы, т. е. если напряжение UаЬ увеличить, например, в 1,3 раза, то токи и 1С увеличатся не в 1,3 раза, а в большее число раз.








