Явление резкого изменения тока в цепи при незначительном измене­нии напряжения на входе будем называть триггерным эффектом в последовательной феррорезонансной цепи.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если схему рис. 15.43, а подключить к источнику напряжения U, на­пряжение которого находится в интервале между U_x и U₂, то в схеме установится один из двух возможных режимов. Первый режим соответ­ствует положению рабочей точки на участке между точками / и 2, вто­рой — на участке между точками 3 и 4.

На каком из двух участков окажется рабочая точка, зависит от харак­тера переходного процесса в цепи при подключении ее к источнику ЭДС.

Феррорезонансом напряжений называют режим работы цепи (см. рис. 15.43, а), при котором первая гармоника тока в цепи совпадает по фазе с напряжением 0 источника ЭДС. На рис. 15.43, б построены ВАХ для действующих значений: феррорезонанс напряжений приблизитель­но соответствует точке р (находится немного левее ее).

Феррорезонанса напряжений можно достичь изменением величины напряжения или частоты источника питания схемы, а также изменением емкости и параметров нелинейной индуктивности.

Пример 157. Кривая I на рис. 15.44, б представляет собой ВАХ нелинейной индук­тивности. Полагая 7? —> О, определить емкость конденсатора, который следует включить последовательно с нелинейной индуктивностью (см. рис. 15.43, а), чтобы триггерный эф­фект происходил при 60 В. Во сколько раз после скачка /₄ будет больше тока до скачка /₂, если со - 314 с"¹?

Р ешен и с. Из точки U = 60В, / = 0 проводим касательную к ВАХ индуктивнос­ти. Касание произойдет в точке а. ВАХ конденсатора (прямая) должна быть проведена из начала координат параллельно касательной. Тангенс угла наклона ее к оси абсцисс чис­ленно равен 1/(соС).

Из рис. 15.44, б находим 1/(соС) = 600 0м: С = 10⁶/(3]4-600) = 5,32мкФ.

Ток при скачке изменяется с /₂ - 0,06 А до /₄ =* 0,315 А; /₄ //₂ = 5.

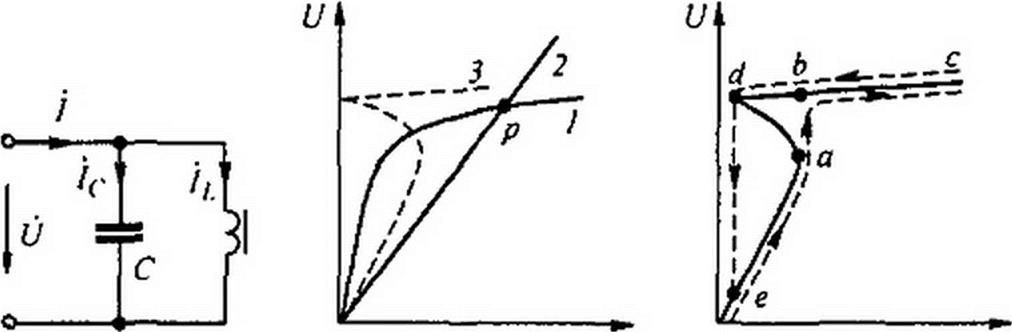
§ 15.60 ВАХ параллельного соединения конденсатора и нелиней­ной индуктивности. Феррорезонанс токов. В схеме на рис. 15.45, а параллельно соединены нелинейная индуктивная катушка L и конденса­тор емкостью С. ВАХ катушки со стальным сердечником изображена кривой 1 на рис. 15.45, б, а конденсатора — прямой 2.

I 1

а б в

Рис. 15.45

По первому закону Кирхгофа / = + /, .Так как токи и I, нахо­

дятся в противофазе, то точке р пересечения кривой 1 и прямой 2 соот­ветствует режим феррорезонанса токов — ток / = 0. Результирующая ВАХ всей схемы изображена в виде штриховой линии 3 рис. 15.45, б (аб­сциссы кривой 3 равны модулю разности абсцисс кривой / и прямой 2). Кривая 3 рис. 15.45, б повторена на рис. 15.45, в с тем отличием, что на рис. 15.45, в учтено, что в режиме феррорезонанса токов (точка d на рисунке) ток / в неразветвленной части схемы до нуля не снижается за счет наличия высших гармоник и активной составляющей первой гар­моники в токе /,.

§ 15.61 Триггерный эффект в параллельной феррорезонансной цепи. Если схему (см. рис. 15.45, а) питать от источника напряжения, плавно увеличивая напряжение этого источника при неизменной часто­те, то изображающая точка пройдет без скачков по всем участкам ВАХ схемы. Если же схему питать от источника тока, то при плавном увели­чении тока этого источника и неизменной угловой частоте со изобража­ющая точка будет сначала перемещаться по участку 0—е—а, затем про­изойдет скачок из а в Ъ, после этого движение будет происходить по уча­стку b—с. При последующем плавном уменьшении тока движение будет происходить от с через b к d, затем произойдет скачок из d в е и далее от е к 0. Обратим внимание на то, что режим феррорезонанса токов в схеме на рис. 15.45, а и режим феррорезонанса напряжений в схеме на рис. 15.43, а могут быть достигнуты изменением входного напряже­ния U при фиксированных угловой частоте со, емкости С и неизменной ВАХ нелинейной индуктивности.

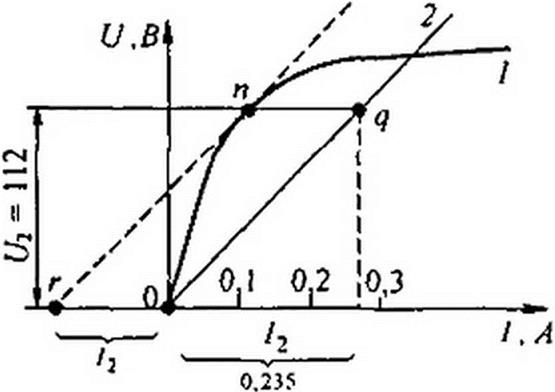
Пример 158. ВАХ каггушки со стальным сердечником в схеме на рис. 15.45, а изобра­жена в виде кривой / на рис. 15.46. Пренебрегая резистивным сопротивлением и высши­ми гармониками, определить емкость конденсатора С, который нужно включить в схеме

на рис. 15.45, а, чтобы триггерный эффект имел место притоке /₂=0,15А; со = 314с .

Решение. На рис. 15.46 откладываем значение тока /₂ влево от точки 0; получаем точку г. Из нее проводим штриховой касатель­ную к кривой / в точке п. Через точку п прово­дим горизонталь. Ордината ее равна напряже­нию 1/₂ = 112В, при котором произойдет триггерный скачок. Из точки 0 проводим пря­мую 2. параллельную касательной гп. Прямая 2 представляет собой ВАХ конденсатора. Абсцис­са точки q (0,265 А) равна току через конденса­тор при напряжении {Jo. Следовательно, 1 / (о О = 112 / 0,265 = 422 Ом; С = 7,54 мкФ.

§ 15.62 Частотные характеристики нелинейных цепей. Под амп­литудно-частотной характеристикой (АЧХ) понимают зависимость амплитуды какой-либо величины, определяющей работы нелинейного элемента, от изменения угловой частоты при неизменной амплитуде внешнего воздействия.

Фазочастотная характеристика (ФЧХ) — зависимость фазы этой величины от о при неизменной амплитуде и фазе внешнего воздействия. В отличие от линейных цепей формы АЧХ и ФЧХ нелинейных цепей зависят от амплитуды внешнего воздействия, т. е. можно рассматривать семейства АЧХ и ФЧХ, для которых амплитуда внешнего воздействия является параметром.

Построим АЧХ цепи (рис. 15.47, а), полагая, что вебер-амперная ха­рактеристика нелинейной индуктивности описывается формулой i₂ = а чА ток источника тока j_k = l_m sin со t, Г_т ~ const, со = var, /?-0.

г> • , . ■ du_c d¹ ц/ . з

В уравнении + 1₂ = j_k подставим = С ~ С - и i₂ - а у.

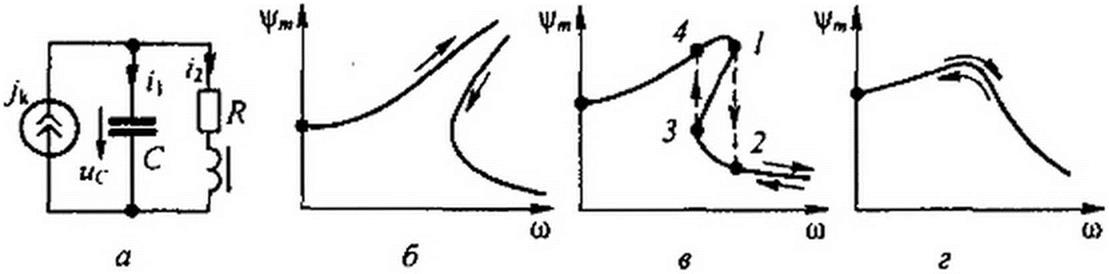
Рис. 15.47

Примем ц/ = sin он ив токе /₂ удержим’’ только первую гармони­ку — 0,75 а sin со г Получим уравнение, в которое входят со и :

0,75 yj, -и? Су_т=±1_т.

Плюс в правой части соответствует режиму до резонанса, минус — после резонанса. Решим уравнение относительно со:

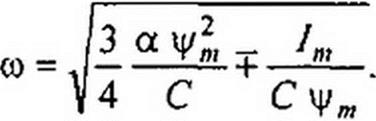
При построении зависимости у_т(о) учтем, что угловая частота со > 0 и действительна, а также что при х« 1 vl ±х ~ I ±0,5 х.

Если со = 0, то \у_т = V⁴ /(3 «)• При 0,75 а » ^{_т

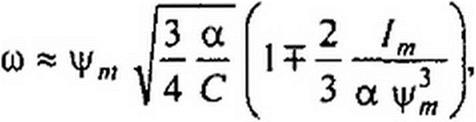
при /„ > 0,75 а ч4

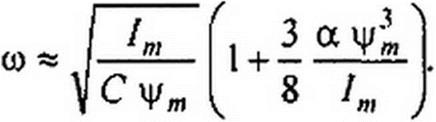
Характер зависимости ц/„,(со) показан на рис. 15.47, б. Если не учи­тывать резистивное сопротивление R второй ветви, то теоретически могла бы возрастать до бесконечности. С учетом небольшого R этой ветви зависимость Ц/_т(со) имеет /V-форму (рис. 15.47, в).

При плавном увеличении со имеет место скачок из точки / в точку 2; при последующем плавном уменьшении со — скачок из точки 3 в точ­ку 4. При значительном R зависимость ц/_т(со) приобретает вид кривой на рис. 15.47, г.

§ 15.63 Применение символического метода для расчета нелиней­ных цепей. Построение векторных и топографических диаграмм. В § 15.56-15.62 были рассмотрены некоторые явления, которые анали­зировались графически с помощью ВАХ, по действующим значениям или

§ 15.64 = а sin© /)³ = а — sin<o/-a 0,25 sin©/, так как sin³0 = 0,75 sinp - 0,25sin3p. ⁴

по первым гармоникам. Приближенное исследование режимов работы сложных разветвленных нелинейных цепей переменного тока, особенно когда высшие гармоники выражены слабо, часто проводят с помощью векторных или топографических диаграмм.

Диаграммы строят отдельно для каждой из гармоник. Построения выполняют в принципе так же, как и для линейных цепей (см. § ЭЛ 8). Отличие состоит в том, что зависимость первой гармоники напряжения на нелинейном элементе от первой гармоники тока через него является нелинейной и берется из графика или ее подсчитывают, пользуясь ана­литическим выражением.

Если не учитывать потери в ферромагнитном сердечнике и потери от высших гармоник тока, то первая гармоника напряжения на нелинейной индуктивности по фазе на 90° опережает первую гармонику тока через нее. Если же учитывать потери в стали сердечника и (или) потери в ре­зистивных сопротивлениях цепи от высших гармоник тока, то этот угол меньше 90° (см., например, рис. 15.50, в). Аналогично, если не учиты­вать наличие потерь в сегнетодиэлектрике и потерь в цепи от высших гар­моник тока, то первая гармоника напряжения на нелинейном конденса­торе на 90° отстает от первой гармоники тока через него.

При учете потерь в сегнетодиэлектрике и потерь от высших гармо­ник 1/_с1 отстает от /_с| на угол меньше 90°.

При построении векторных диаграмм для высших и дробных гармо­ник на частоте v f следует иметь в виду, что при синусоидальном ис­точнике питания частоты f нелинейный индуктивный (емкостной) эле­мент схемы является источником энергии на частоте v /, поэтому напряжение на частоте v f на нелинейном индуктивном элементе будет опережать протекающий через него ток /_v/- частоты v f на угол больше 90° (а на емкостном напряжении U_Cvf будет отставать от Л/ на угол больше 90°).

Обобщенно можно сказать, что комплексное сопротивление нелиней­ного элемента НЭ на частоте v f (v ф 1) при частоте источника пита­ния f равно взятому со знаком минус входному сопротивлению линейно­го двухполюсника на частоте v f, к зажимам которого присоединен НЭ.

В случае линейного активного четырехполюсника (см. рис. 4.16, п) с внутренними источниками частоты/ заменив источник ЭДС частоты/в ветви I на нелинейный элемент НЭ] и линейную нагрузку Z_H в ветви 2 на НЭ₂ на любой гармонике v f (v * 1) в схеме установится режим, при котором Z_BXH31(^V )^s~^ci(^v/) И Z_BxH3₂(v) = “Z_c2(v/), где Z_cl(v /) и Z_c2(v /) — характеристические сопротивления линейного четырехпо­люсника по отношению к ветвям / и 2 на частоте v f определяемые по (4-47).

Пример 159. Для цепи (рис. 15.48, а) построить топографическую диаграмму по пер­вой гармонике при !_} - 0,2 А. ВАХ по первой гармонике для нелинейной индуктивности изображена на рис. 15.48, б. Емкостное сопротивление по первой гармонике Х_с - 229 Ом; Д, = 250 Ом; Д₂ = ⁴⁰⁷ Ом; Д₃ = 122 Ом.

Решение. Обозначим токи в ветвях и узловые точки схемы в соответствии с рис. 1.5.47, а. На рис. 15.48, в направим ток /₁₌0.2А по оси +1. Потенциал точки е при­мем равным нулю. Находим <j>^=<P_e⁺^z,i Напряжение на нелинейной индуктивности

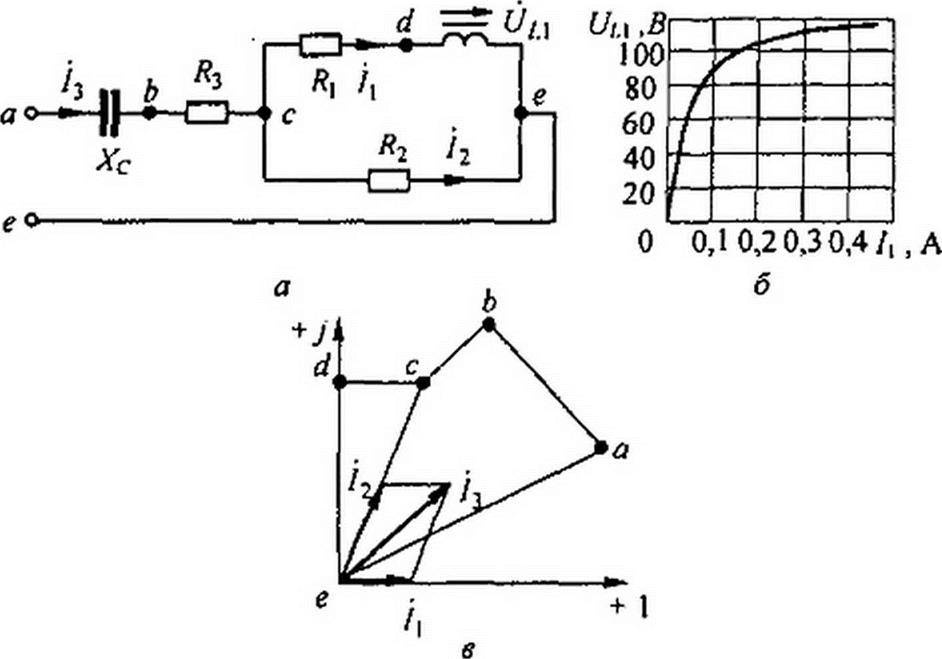
Рис. J 5.48

(//j при токе /j =0.2 А по модулю равно НО В (найдено из кривой на рис. 15.48, б) и по фазе на 90° опережает ток ф_с = + 4 !_} R_} = 0.2-250 = 50 В и по фазе со­

впадает с /].

Под действием напряжения по модулю приблизительно равного 122 В, протека­ет ток /₂* численно равный 122/407 *0,3 А и по фазе совпадающий с 0_се. Ток Л=/| + /2.. По модулю ток 4 *0.41 А; ф_Л = ф₄, + i_} R₃; i₃ R₃ =0,41-122 = 508; Фа = Фл + h <~J *(')•

Напряжение на конденсаторе U_ak численно равно 0,41-229 = 94 В и по фазе на 90° отстает от тока 4-

Напряжение на входе схемы (см. рис. 15.48, а) в рассматриваемом режиме работы по модулю равно 164 В.

Из рис. 15.48, в можно определить углы между любыми токами и напряжениями цепи рис. 15.48,0. Проделав аналогичные подсчеты и построения при других значениях тока (например, равных 0,5; 1; 2; 3 А и т.д.), можно определить в этих режимах значения всех токов, напряжений и сдвигов фаз, свести данные в таблицу и затем, пользуясь ею, построить кривую зависимости любого тока, напряжения, сдвига фаз в функции от моду­ля входного напряжения или от модуля какого-либо другого напряжения (тока).

§ 15.64 Применение метода эквивалентного генератора. Расчет нелинейных цепей переменного тока иногда осуществляют, используя метод эквивалентного генератора (МЭГ). Рассмотрим применение этого метода к цепи с управляемым нелинейным элементом.

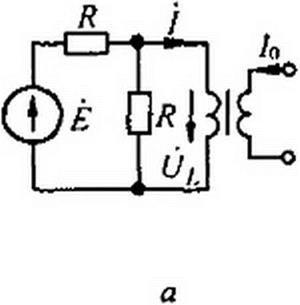
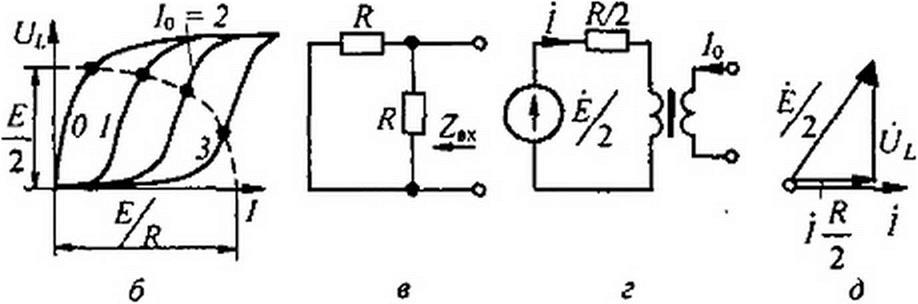
На рис. 15.49, а изображена схемы, состоящая из источника синусо­идальной ЭДС Е, двух резисторов R и управляемой индуктивности (УИ), семейство ВАХ которой по первым гармоникам изображено на рис. 15.49, 6. Ток управления /₀ является параметром на этом семействе. Ток через УИ обозначен /. В соответствии с МЭГ разомкнем ветвь, по которой течет ток /, и определим напряжение (7_аЛх » Е/2 в режиме хо­лостого хода. Определим входное сопротивление Z_8X в цепи перемен­ного тока относительно зажимов а и Ь. В соответствии с рис. 15.49, в оно равно /?/2. На рис. 15.49, г показана эквивалентная схема цепи, а на рис. 15.49, д изображена векторная диаграмма для этой цепи. Геометри-

ческая сумма вектора 1 R/2 и напряжения на нелинейной индуктивнос­ти U_f равна Ё/2. Так как Е/2 является гипотенузой прямоугольного треугольника, катеты которого равны U, и / Я/2, то по теореме Пифа­гора

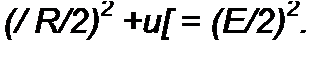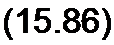Поделив обе части (15.86) на (Е/2)², получим уравнение эллипса:

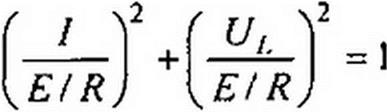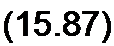Одна полуось эллипса равна (E/R), другая— Е/2. Нанесем эллипс на семейство ВАХ индуктивности (рис. 15.49, б). По точкам пересечения эллипса с ВАХ можно определить ток I и напряжение U _{ на индуктив­ности при любом значении управляющего тока /₀.

При рассмотрении характеристик управляемой индуктивности (см. § 15.24), феррорезонансных схем (см. § 15.57-15.63) индуктивность полагали идеализированной, а именно не учитывали потери в ее сердеч­нике, наличие потока рассеяния и падение напряжения в резистивном сопротивлении обмотки. Это делалось с той целью, чтобы основные свой­ства упомянутых схем и устройств не были завуалированы относитель­но второстепенными факторами.

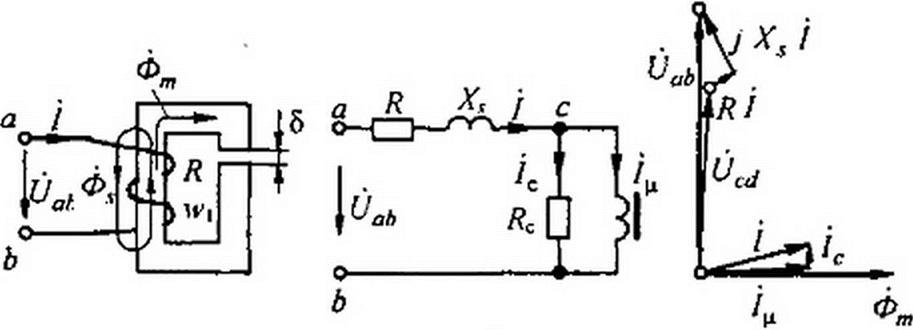
§ 15.65 Векторная диаграмма нелинейной индуктивности с уче­том потока рассеяния и резистивного сопротивления обмотки. Не­линейная индуктивность изображена на рис. 15.50, а. Резистивное сопро­тивление обмотки и/, обозначим R.

Проходящий по обмотке ток создает в сердечнике магнитный поток. Большая часть этого потока (поток Ф„,) замыкается по сердечнику, а меньшая часть (поток Ф_Л.) — по воздуху. Поток Ф_т называют основ­ным, а Ф_Л. — потоком рассеяния.

Обычно поток Ф_Л. составляет всего несколько процентов от потока Ф_т. Однако могут быть и такие режимы работы, в которых поток Ф_ч оказывается соизмеримым с потоком Ф_я?. Такие режимы имеют место, если сердечник работает при большом насыщении или когда в сердеч­нике имеется относительно большой воздушный зазор 6.

При построении векторной диаграммы заменим в действительности несинусоидальный ток и несинусоидальный поток эквивалентными си­нусоидальными величинами.

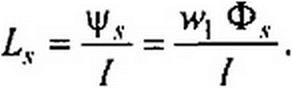Отношение потокосцепления рассеяния \р_Л = ю_} Ф_д. к току / называ­ют индуктивностью рассеяния:

(15.88)