Диод открывается, когда напряжение на нем, увеличиваясь, стано­вится равным нулю, и закрывается, когда ток через него, уменьшаясь, становится равным нулю.

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Рассмотрим работу мостовой схемы (см. рис. 15.36, а). Источник ЭДС включен в одну диагональ этой схемы, а нагрузка /?_н — в другую. Дио­ды работают попарно.

В первый полупериод, когда ЭДС е(г) действует согласно с положи­тельным направлением напряжения на диодах 1 и 3, эти диоды проводят ток, а диоды 2 и 4 тока не проводят. Во второй полупериод, когда ЭДС е(/) изменит знак и действует согласно с положительным направ­лением напряжения на диодах 2 и < эти диоды проводят ток, а диоды 7 и 3 не проводят. Направление прохождения тока через нагрузку показано на рис. 15.36, а стрел­кой. Ток через нагрузку протека­ет все время в одном и том же направлении. Форма напряжения на нагрузке иллюстрируется кри­вой на рис. 15.36, 6. Через обозначено среднее значение на­пряжения на нагрузке.

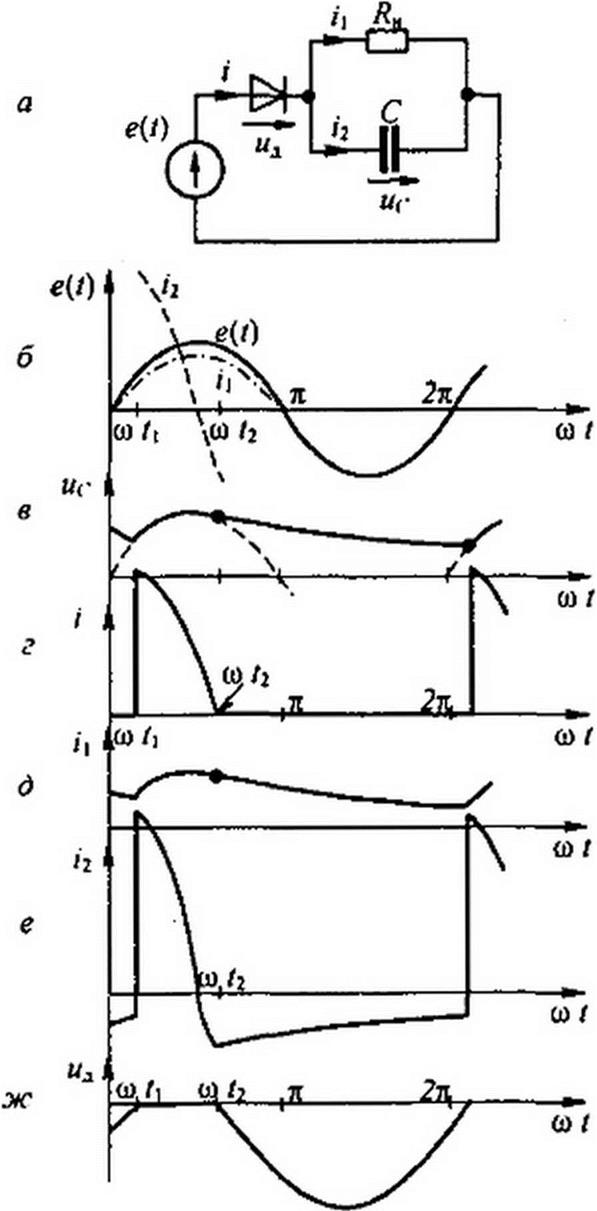
Пример 156. Рассмотреть работу схемы однояолупериодного выпрямле­ния, когда нагрузка /?_н шунтирована конденсатором емкостью С (рис. 15.37, а).

Р е ш е н и е. По законам Кирхгофа, + и_с = е(/); и_с = У, /?_к; , = /, ₊ /₂.

В соответствии с ВАХ (рис. 15.37, е) диод закрыт и сопротивление его теоре­тически равно бесконечности, когда на­пряжение на нем и_а отрицательно. Диод открывается в момент со /_ь когда напря­жение на нем и_Л=е(1)-и_с, увеличива­ясь, становится равным нулю. Как толь­ко диод откроется, напряжение на конденсаторе становится равным ЭДС и_с = Е„ sin со/ и ток через конденсатор станет изменяться по закону

= С —= со С Е_т cosco t (штриховая at

линия на рис. 15.37,о), а ток через на- ^ис •

грузку — по закону /,=-£- = —— sm со /

(штриховая линия с точкой на
рис. 15.37, б). Ток через диод г = z,+г₂ = £_m (coC cosa/ +— sinco/) (рис. 15.37,г) в момент фг₂ становится равным нулю и диод закрывается; tg<oz₂ = -<аС Я_н; <и/₂ =arctg(~0C /?_к).

В интервале от и/₂ до 2 п + (о /) конденсатор разряжается на Л_н (рис. 15.37, а) и напряжение на нем изменяется во времени по показательному закону u_c = Е„ sin со /₂ е ®^СЛ* ; (см. гл. 8). При этом ii=u_c/R„ (кривые на рис. 15.37, д. е). За­висимость u_a(wr) изображена на рис. 15.37, ж. Момент открытия а> диода определим из условия х/Дсв /)) = е(со г_г). Из этого условия получаем трансцендентное уравнение от­носительно о ;

(2я+(од-(о/2)

sincaf₂ е ssino/p

В следующий период процесс повторяется. Чем больше значение R_M С по сравнению с периодом 2 л/со, тем меньше пульсация напряжения на нагрузке R_H.

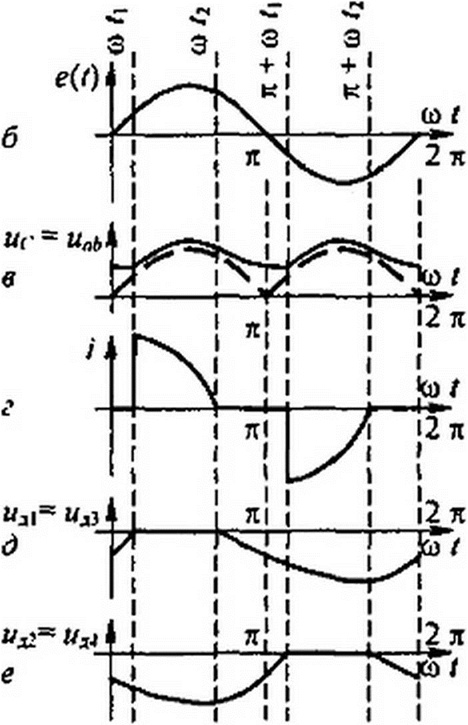
§ 15.52 Мостовая схема выпрямления с нагрузкой R, L, Схема изображена на рис. 15.38, а. На входе моста ЭДС е(() - Е_т sinco t. Поло­жительные направления отсчета токов и напряжений на элементах схе­мы показаны стрелками. Диоды работают попарно. В первом полупериоде открыты (пропускают токи) диоды 1 и 3 и напряжения на них ы_Д| и равны нулю, а диоды 2 и 4 закрыты (не пропускают токи) и на каждом из них напряжение равно -0,5 Е_т sin со t. Во втором полупериоде отк­рыты диоды 2 и 4 и закрыты диоды 1 и 3. Временные кривые изображе­ны на рис. 15.38, б-ж. На рис. б — ЭДС е(г), на рис. в— напряжение на зажимах ab моста, на рис. г — принужденный /_пр, свободный z_CB и пол­ный ток i через R и L; рис. д — ток С через источник ЭДС; рис. е — напряжения на диодах / и 3; рис. ж — напряжения на диодах 2 и 4.

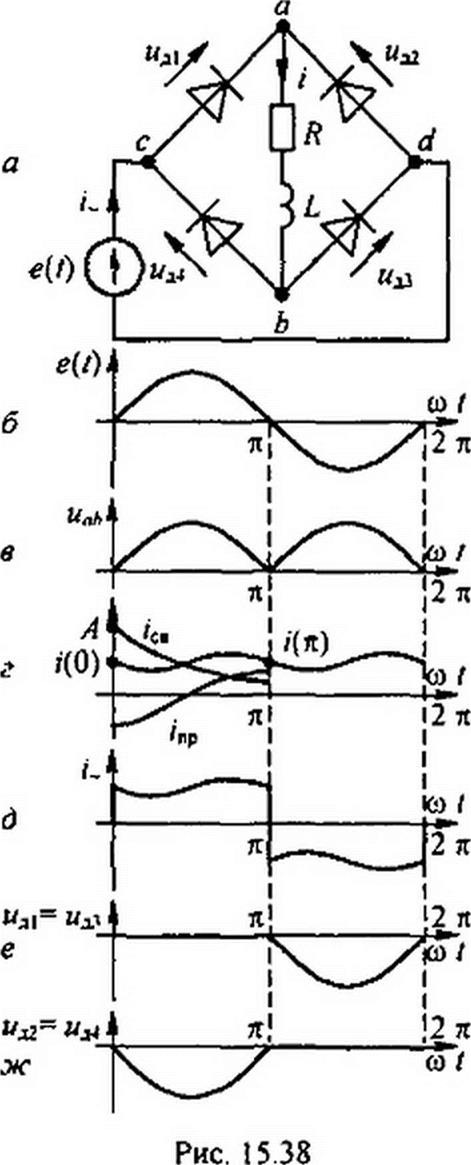
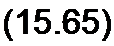Для обоих полу периодов справедливо уравнение (15.65), составлен­ное по второму закону Кирхгофа,

L — + Ri = Е„. sin со /. dt

Решение уравнения (15.65) классическим методом для первого полу­периода / = /_пр +/_са = — sin(ci) г - <р) + Ае^р1. Здесь z = V/?² +(cn L)², ср = arctg

Характеристическое уравнение R + р L = 0 имеет корень p = -RI L. Из условия периодичности процесса /(0) = /(л), поэтому

sin ср + А = —— sin ср + А е “

Следовательно, постоянная интегрирования

2 — sin ф

(15.66)

к
(и L

Для определения среднего за полупериод значения тока / (обозначим его Г) проинтегрируем уравнение (15.65) за интервал времени (О-гГ/2) ^{7 7 2} di

и учтем, что [ — dt = /(л) - /(0) = 0. Результат интегрирования поделим о ^Л

на Г/2 и получим

(15.67)

Из формулы (15.67) следует, что ток /_ср в схеме на рис. 15.38, а не зависит от величины индуктивности L. Однако L выполняет важную роль, снижая пульсации выпрямленного тока.

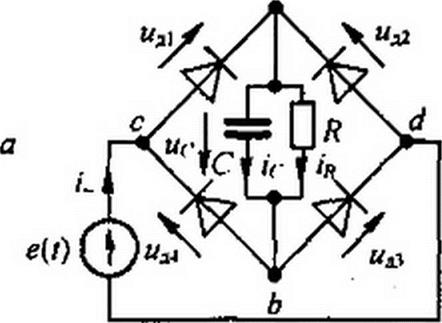
§ 15.53 Мостовая схема выпрямления с нагрузкой RC. Схема изоб- ражена на рис. 15.39, а. К входным зажимам моста cd присоединена ЭДС е(/) = Е_т sin о) /, к выходным зажимам ab — нагрузочное сопротивление /?, шунтированное конденсатором С. Обозначения токов и напряжений на элементах схемы показаны на рис. 15.39, а. Как и в предыдущей

схеме, диоды работают попарно. Временные графики изображены на рис. 15.39, б-е. Запишем систему уравнений по законам Кирхгофа:

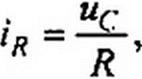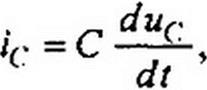^М д1 - ^и д2 = ^Ет ^sin « h + »д2 = "“С •

Из двух последних уравнений следует, что

*Д| = *дЗ = °’⁵(^Ет sinco/-w_c) и ЙД2 = и_д4 = -0,5(Е_т sinшt + u_cY

В первом полупериоде в интервале со / = 0 oj / = to /, ив интервале со t₂ п все диоды закрыты, т. е. не пропускают тока, так как напряже­ния на них отрицательны (в эти интервалы и₍- > e(f)). В интервале вре­мени О-to/j конденсатор разряжается на R. При со^ напряжение на конденсаторе и_с становится равным Е_т sin to и диоды 1 и 3 открыва­ются, но диоды 2 и 4 остаются закрытыми. В интервале от to г, до to /₂

и_с = Е_т sin to t

и конденсатор подзаряжается током /_с - to С Е„, cos со Г, а через резистор течет ток

/о = —— sin to t.

^к R

При со t₂ ток / = + i_c становится равным нулю, диоды 1 и 3 закры­ваются и зарядка конденсатора прекращается. Время со/₂ определим из уравнения со R С cosco t₂ ч- sin со t₂ =0. Из него находим

со /₂ = ” arctg со R С.

(Сравните с определением со г₂ ^в примере 156.)

В интервале от <о/₂ до (л + со конденсатор разряжается на R, на­пряжение и_с уменьшается от и_с (со /₂) - E_ni sin со t₂ до значения и_с (n4-to/|)= Е_т sin со Гр В этот момент времени

(л-*-<0 -со/₂)

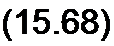Е„, sinco/₂e ^ш/?< =£_/Msinco/_l.

Из (15.68) получим трансцендентное уравнение для определения со :

sinco/₂e =sinto/!.

После определения co z, можно определить и_с(0) по уравнению

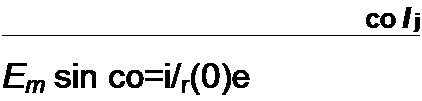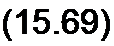При со / — л + cd /j открываются диоды 2 и 4 и выполняют во втором полупериоде ту роль, которую в первом полупериоде выполняли диоды 1 и 3. С увеличением емкости конденсатора С пульсация напряжения и_с уменьшается.

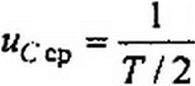
Среднее за полпериода значение выпрямленного напряжения

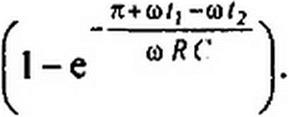sin со t₂

— (COSCOZj -coscdz₂) +----- Е_т sin coz₂

n T

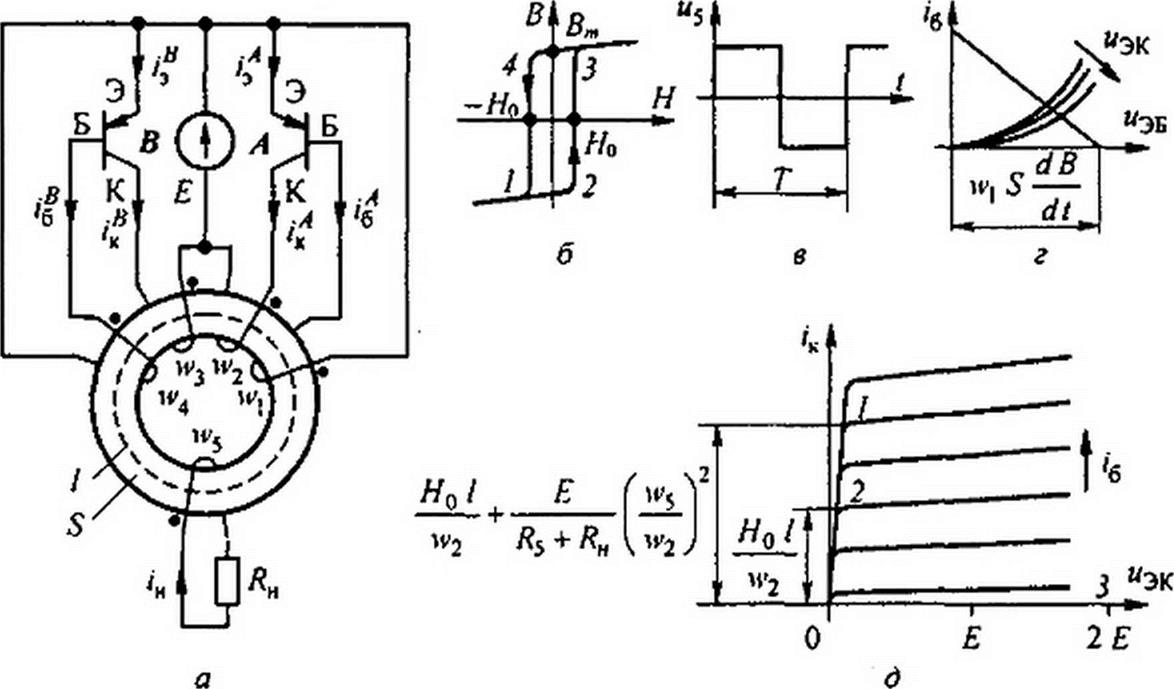
§ 15.54 Анализ работы магнитно-транзисторного генератора пря­моугольного напряжения. Схема генератора изображена на рис. 15.40, а. Она содержит трансформатор, два биполярных транзистора А и В р—п—/7-типа и источник постоянной ЭДС Е. Пермаллоевый сердечник трансформатора имеет почти прямоугольную динамическую петлю гис­терезиса. Зависимость магнитной индукции В сердечника от напряжен­ности магнитного поля Н в нем изображена на рис. 15.40, б. Остаточная индукция в сердечнике при Я = 0 обозначена В_т. Коэрцитивная сила — Hq. Площадь поперечного сечения сердечника назовем S, дли­ну средней магнитной линии его — 7. На сердечник нанесено пять об­моток (катушек) с числами витков wj ~ w₅. Катушка с числом витков Wj управляет режимом работы транзистора А, катушка с числом витков управляет режимом работы транзистора В. Катушка с числом витков w₂ является основной рабочей обмоткой, на которую работает транзистор А в первом полупериоде. Катушка с числом витков w₃ — основная рабо­чая обмотка, на которую работает транзистор В во втором полупериоде. Катушка с числом витков w₅ — выходная обмотка, в ней генерируется напряжение w₅ в виде меандра (см. рис. 15.40, в), и к ней присоединено нагрузочное сопротивление Я_и.

Начала всех катушек обозначены точкой на рис. 15.40, а. Направле­ния намотки на сердечник всех катушек одинаково.

Резистивные сопротивления катушек -rw₅ обозначим /?| +R_S, чис­ла витков и’_!=и'₄, w₂ = и>₃ и /?₂ ⁼ ^3' Катушка с числом

витков w₅ имеет сопротивление Л₅. Числа витков и w₄ много мень­ше чисел витков w₂ и w₃.

Обозначим токи и напряжения транзистора A: i£ —ток базы; — ток эмиттера, — ток коллектора, — напряжение между эмитте­ром и базой; — напряжение между эмиттером и коллектором. Тран­зистор А находится в рабочем состоянии i* > 0, если > 0 (при этом база транзистора А имеет отрицательный потенциал по отношению к эмиттеру транзистора Л). Токи и напряжения транзистора В обозначим аналогично: /§ , , i* и и”_к. Транзистор В будет находиться в

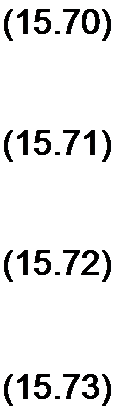рабочем состоянии (м^ > 0), когда > 0. Составим систему уравне­ний по второму закону Кирхгофа:

"ЭБ + 'б Л ~ ^w i $ ~т~ ~ $ at

А -А лч d В —

"ЭК ⁺ 'к ^R 2 ^{+ w} 2 S at

^и ЭБ ⁺ ^4 ^{+ lv}4 $ ~

at

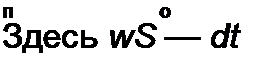"эк + '* ^“"з S — = E.

— напряжение на соответствующей обмотке w между

ее началом и концом. В первом полупериоде изображающая точка по петле гистерезиса сначала перемещается по участку 2—3, на котором перемещается по почти горизонтальному участку 3—4, на котором

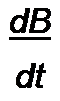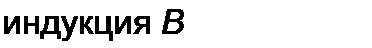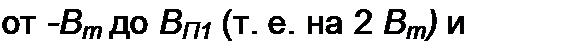< 0. При движении по участку 2—3 > 0, а < 0, поэтому тран-

dt зистор А находится в рабочем состоянии j* > 0, а транзистор В — в не­рабочем и ток i* - 0 в соответствии с уравнениями (15.70) и (15.72).

Так как величина £ практически много больше суммы и^_к +i* R₂, то при движении по участку 2—3 можно в первом приближении принять

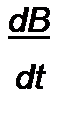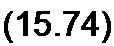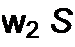В уравнении (15.74) разделим переменные и проинтегрируем его по индукции от ~В_т до В_т> а по времени от 0 до.Т/2, где Т — пе­риод движения по гистерезисной петле. Получим w₂ S2B_m -ЕТ!2. Отсюда

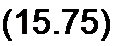4 В_п, w₂ £ _z £

—-—-—, а частота / ----- --------------------------------

£ 4 В_т w₂ 3

Хотя при быстром движении по участку 3—4 гистерезисной петли dB

производная -j— отрицательна и мала по величине, но числовые значе­ния и_ЭБ обоих транзисторов при этом оказываются достаточными, что­бы закрыть транзистор А (его станет меньше нуля) и открыть тран­зистор В (его й_ЭБ станет больше нуля).

После этого начнется вторая половина процесса, когда при «эб <0 под действием транзистора В происходит движение изображающей точ­ки по участку 4—]—2 гистерезисной петли. Определим теперь положе­ние рабочих точек для обоих транзисторов на общем для них семействе кривых 7_б =Днэк) Р^ис* 15-40, д при движении изображающей точки по участку 2—3 гистерезисной петли для двух случаев:

1) к зажимам обмотки м>₅ присоединено сопротивление /?_н;

2) случай холостого хода.

По закону полного тока магнитодвижущая сила катушек с токами трансформатора должна быть равна произведению напряженности маг­нитного поля H_Q на длину / средней магнитной линии сердечника, т. е. в первом полупериоде

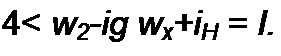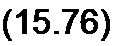Так как w₂ «4* w₂, то i* w₂ + i_H w₅ = H_o I.

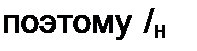
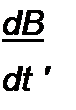dB

Ho m>₅ S — + 4 (/?₅ + ) = 0, dt

O ^B Г' /

w₂ S — ~ £, то в первом случае (при

H„l Е fw.y . . .Л Н_а1

—— +------------ — , а во втором (при холостом ходе) =——

w₂ /?₅+tf_H<w₂J w₂

В первом полупериоде рабочая точка для транзистора А будет нахо­диться на семействе кривых (рис. 15.40, д) при нагрузке в точке 1, а при холостом ходе — в точке 2.

Точка 3 (/_к = 0, ы_ЭБ = 2 £) определяет положение рабочей точки тран­зистора В в первом полу периоде. Во втором полу периоде транзисторы меняются положениями своих рабочих точек.

Частоту f можно изменять, варьируя величину ЭДС Е или число вит­ков w₅. Практически частоту можно изменять от долей герца до несколь­ких килогерц.

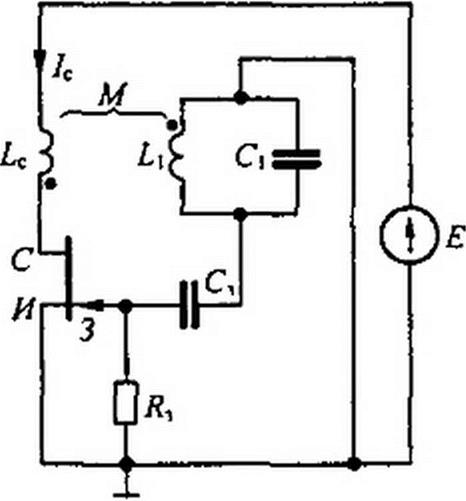
§ 15.55 Автоколебания. Автоколебания (АК) — это периодические колебания, возникающие в системах, находящихся под воздействием по­стоянных во времени вынуждающих сил. АК-системы подразделяют на почти гармонические (см. § 15.55) и релаксационные (см. § 17.5). АК-система на полевом транзисторе изображена на рис. 15.41, а. В ней имеются источник постоянной ЭДС £, колебательный контур Ц, С\ и взаимная индуктивность М между и £_с, за счет которой в системе осуществляется отрицательная обратная связь.

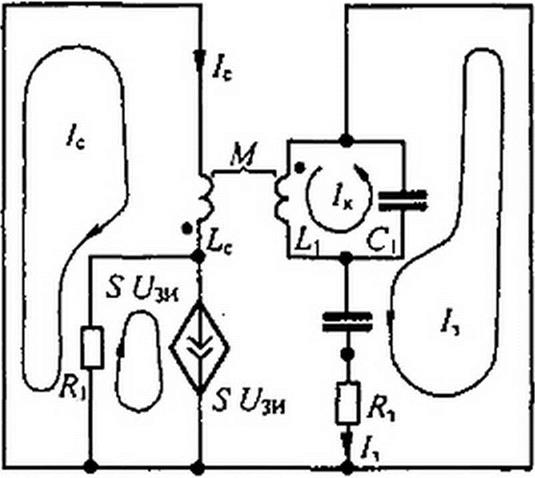
При анализе АК-систем почти гармонического типа требуется выяс­нить частоту и амплитуду возникающих колебаний и характер возбужде­ния (мягкий или жесткий). На рис. 15.41, б изображена схема замещения для переменных составляющих токов и напряжений. Источник постоян­ной ЭДС закорочен. Транзистор представлен источником тока >5(7_ЗИ, управляемым напряжением С/_Зи, и шунтирующим его резистором R_}.

Составим уравнения по методу контурных токов. В схеме три неиз­вестных контурных тока — /_с, /_к, 1₃ — и один ток источника тока — (1/_зиЧ*з):

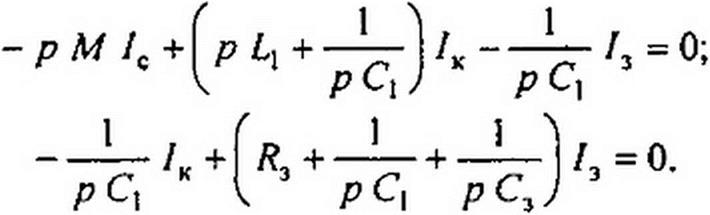
(15.77)

При АК токи не равны нулю, это может быть только в том случае, если главный определитель системы (15.77) равен нулю:

Д(Р) = Р⁴ (*з * С,² С₁₃) + р³ {к С,² + R, R₃ L_x С² С₁₃) +

+ р² (Я₃ L_c С_} С₁₃ + ItC)²’-/?, 5/?₃Л/С₁С₁₃)+ (15.78)

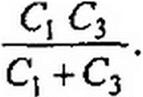+ p(R_} R₃ q C_l3 + L_C (C,-C₃)) + R_x (Q -q₃) = 0.

Здесь k = L_x L_c-M², C_x3 =

В Д(р) подставим p = j co, выделим из него действительную и мни­

мую части и приравняем их нулю. После деления всех членов уравне­ния ReA(y<i)) = 0 на R₃C_X С₁₃ получим

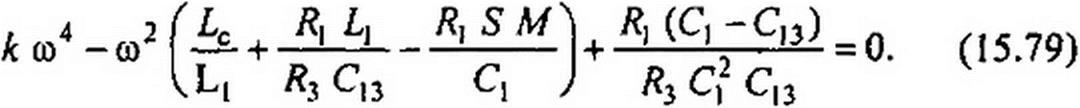После деления всех членов уравнения 1тД(_/ w)==0 на С² С₁₃ и со­кращения на со имеем

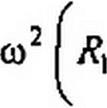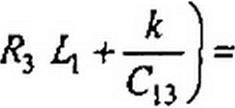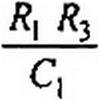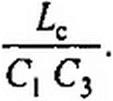Отсюда

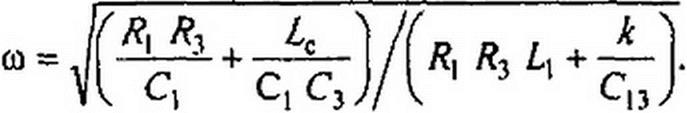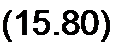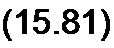
При весьма больших R₃ со = l/^i С_х и крутизна

S = A//(K_t L_x).

§ 15.56 Мягкое и жесткое возбуждения автоколебаний. Ток стока транзистора i_c является функцией напряжения й_зи. Эта функция может быть представлена кривой рис. 15.42, а, приближенно описываемой зависимостью

(15.82)

либо кривой рис. 15.42, б, описываемой формулой

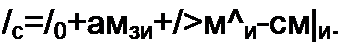При возникновении АК м_зи = sin со /. Подставим это ы_зи в (15.82) и (15.83) и определим амплитуду первой гармоники тока /_с. Из формулы (15.82) она равна I_cm = a U_m - 0,75 b а из (15.83) /_ст=а<7„+0,75*4^

Под средней крутизной по первой гармонике в режиме автоколеба­ний понимают $_ср = Она выполняет роль крутизны 5 в форму­

лах (15.79) и (15.80). Для первого случая (рис. 15.42, в)

S_cp = а -0,75 bU²_m.

Для второго (рис. 15.42, г)

S_cp = a + 0,75i>^-|^.
О

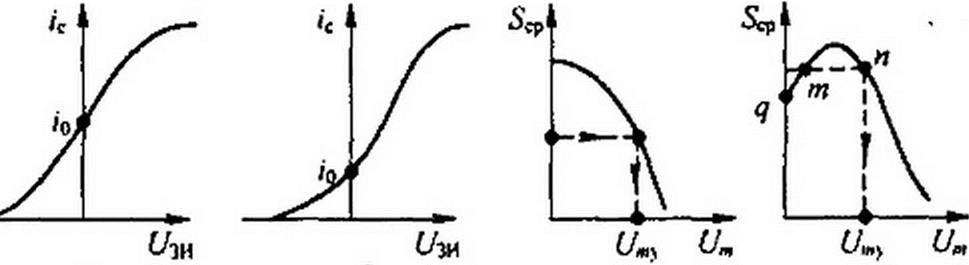
Кривые рис. 15.42, а, г используем для определения амплитуды U_m возникшего колебания. С этой целью из (15.79) или при -><ю из

определим S и положим его равным 5_ср, а по 5_ср из кривой

рис. 15.42,в или г найдем <7_да. В первом случае каждому £_ср соответ­ствует одно U_m, во втором могут соответствовать либо два режима (в области S_cp от q hq S_cpmax точки т и п), либо один режим (при S_cp <q). Режим работы на левой ветви кривой рис. 15.42, г неустойчив, на всей правой («жирной») ветви — устойчив.

Если S_cp определяется кривой рис. 15.42, в, то колебания возбужда­ются мягко, их амплитуда плавно нарастает от сколь угодно малого начального значения флуктуационного происхождения до установивше­гося U_my. Для S_cp по рис. 15.42, г колебания возбуждаются жестко — скачком от нуля до установившегося значения U_niy.

Обратим внимание на то, что генератор, рассматриваемый в § 15.55-15.56, является автоколебательной системой, принципиально отличной от рассмотренной в § 15.54. Действительно, основными эле­ментами схемы рис. 15.41, а являются: источник постоянной ЭДС, управ­ляемый нелинейный резистивный элемент (полевой транзистор), накопи­тели энергии Ц и Cj и резистор R₃. В схеме есть явно выраженная обратная связь, колебания имеют почти синусоидальную форму, частота колебаний равняется собственной частоте системы.

В АК-системе (рис. 15.40, а) основными элементами являлись источ­ник постоянной ЭДС, два управляемых нелинейных элемента (два бипо­лярных транзистора), нелинейный индуктивный элемент (трансформатор с ферромагнитным сердечником). В схеме рис. 15.40, а нет линейных индуктивностей и емкостей, возникающие колебания имели не синусои­дальную, а прямоугольную форму, частота колебаний определялась вре-

менем перемагничивания сердечника, обратная связь проявляла себя не­явным образом — процесс перемагничивания ферромагнитного сердеч­ника управлял работой транзисторов.

§ 15.57 Определение феррорезонансных цепей. Рассмотрим груп­пу довольно грубых явлений, которые имеют место в цепях, содержащих нелинейную индуктивность и линейный конденсатор. Такие цепи назы­вают феррорезонансными. Аналогичные явления имеют место в цепи с линейной индуктивностью и нелинейным конденсатором.

Для анализа этих явлений можно воспользоваться методом первой гармоники (см. § 15.47) или методом расчета по действующим значени­ям (см. § 15.48). В § 15.59-15.62 будет применен метод расчета по дей­ствующим значениям. При этом будем пользоваться ВАХ нелинейной индуктивности для действующих значений тока и напряжения. В этом методе в действительности несинусоидальные токи и напряжения заме­няют их эквивалентными синусоидальными величинами (эквивалент­ность в смысле действующего значения по § 7.12).

Когда в § 15.59-15.62, 15.65, 15.68 рассматривается сдвиг фаз между током и напряжением на каком-либо элементе схемы, то под ним пони­мают угол между эквивалентным синусоидальным током и эквивалент­ным синусоидальным напряжением.

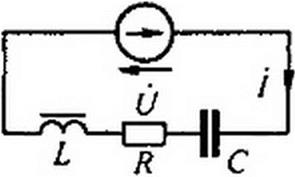
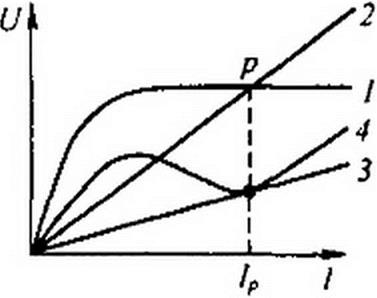
§ 15.58 Построение ВАХ последовательной феррорезонансной цепи. В схеме на рис. 15.43, а последовательно включены нелинейная ин­дуктивность £, линейный резистор сопротивлением R и линейный кон­денсатор емкостью С. ВАХ нелинейной индуктивности U _L - /(/) изоб­

ражается кривой I на рис. 15.43,6; ВАХ конденсатора U₍- = / —— — о С

прямой 2; ВАХ резистора U_R = R I — прямой 3.

Точки, принадлежащие результирующей ВАХ схемы — кривой < по­лучаем следующим образом.

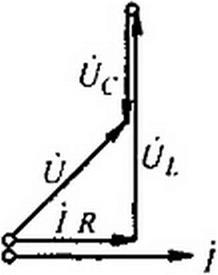
Произвольно задаемся некоторым током /, находим для него разность напряжений U_r -U_(: (напряжения на индуктивности и на конденсаторе находятся в противофазе) и напряжение U_R‘_y результирующее напряже­ние U равно гипотенузе треугольника, построенного на катетах U_R и U_{ -U_с (рис. 15.43, в).

При сравнительно малом R на результирующей ВАХ цепи имеется падающий участок, а сама ВАХ имеет TV-образную форму. С увеличени­ем R падающий участок на ВАХ исчезает.

§ 15.59 Триггерный эффекгт в последовательной феррорезонанс-

ной цепи. Феррорезонанс напряжений. На рис. 15.44, а отдельно пред­ставлена кривая 4 рис. 15.43, б. Будем начиная с нуля плавно увеличи-

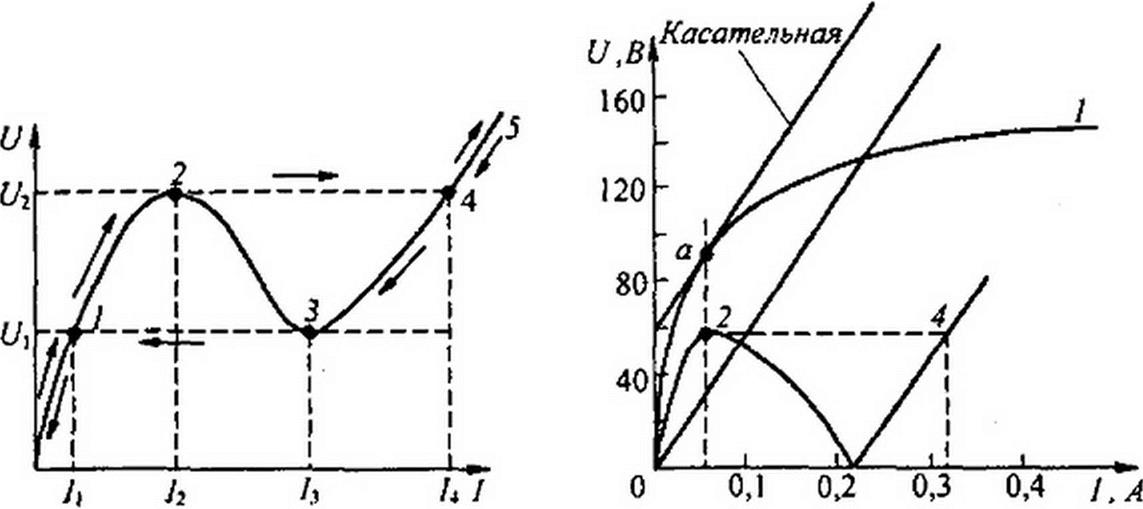
а б

Рис. 15.44

вать напряжение источника ЭДС в схеме 15.43, а. При этом изображаю­щая точка на рис. 15.44, а перемещается от точки 0 через точку / к точ­ке 2. Если напряжение и дальше повышать, то изображающая точка скач­ком переместится из точки 2 в точку 4, а затем движение будет происхо­дить по участку 4—5.

При уменьшении напряжения изображающая точка перемещается от точки 5 через 4 к точке 3, затем произойдет скачок в точку / и далее от точки 1 к точке 0. Таким образом, при увеличении напряжения и дости­жении им значения U₂ в цепи происходит скачкообразное увеличение тока со значения /₂ до /₄. При этом резко изменяется сдвиг фаз между током в цепи и общим напряжением: в точке 2 ток отстает от напряже­ния (<7/ в точке 4 ток опережает напряжение (Ц_с При плавном уменьшении напряжения источника ЭДС и достижении им зна­чения Ц ток в цепи скачком уменьшается со значения до /,.