Напряжение между анолом и катодом иа называют анодным напря­жением, между сеткой и катодом мс — сеточным напряжением.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Ток в анодной цепи /_а и ток в сеточной цепи /_с нелинейно зависят от анодного w_a и сеточного и_с напряжений.

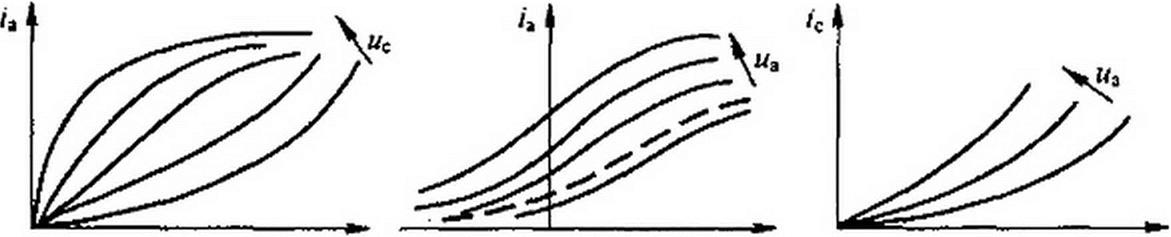
Под анодными характеристиками трехэлектродной лампы понима­ют зависимость анодного тока /_а от анодного напряжения и_а при сеточ­ном напряжении и_с, взятом в качестве параметра.

На рис. 15.29, а изображено семейство анодных характеристик лам­пы. Стрелка на рис. 15.29, а~в указывает направление, в котором возра­стает параметр.

Если семейство анодных характеристик рассечь прямыми w_a - const, то можно получить семейство кривых /_а ~ /(и_с) при параметре и_а. Та­кие кривые называются сеточными {анодно-сеточными) характеристи­ками трехэлектродной лампы (рис. 15.29, б). Для них характерно, что ток 4 * 0 при u_z = 0; кроме того, имеется область насыщения, в которой ток 4 почти не увеличивается с ростом «_с.

Семейство кривых /_с - f{u_c) при различных значениях анодного на­пряжения и положительных значениях и_с для одного из типов ламп изоб­ражено на рис. 15.29, в.

В общем случае при работе лампы одновременно меняются и_а и w_c и изображающая точка на семействах анодных и сеточных характерис­тик перемещается с одних кривых на другие. В частном случае работы, когда и_а остается неизменным или почти неизменным, = f{u_z) изоб­ражается одной кривой семейства кривых (см. рис. 15.29, 6).

Если электронная лампа работает при отрицательных или сравнитель­но малых положительных напряжениях на сетке, то сеточный ток имеет малое значение и его в расчете, как правило, не учитывают.

Следует отметить своеобразие сеточной характеристики по сравнению с обычными ВАХ: сеточная характеристика дает связь не между током через нелинейный элемент и напряжением на нем, что характерно для обычных ВАХ, а между мгновенным значением тока через нелинейный элемент и мгновенным значением управляющего напряжения на нем.

§ 15.39 Аналитическое выражение сеточной характеристики электронной лам­пы. Связь между малыми приращениями входных и выходных величин электрон­ной лампы. Сеточная характеристика при w_a = const может быть приближенно представ­лена отрезками прямых (рис. 15.30). Часть сеточных характеристик, например характери­стика, выделенная жирной линией на рис. 15.29, б. может быть описана полиномом тре­тьей степени:

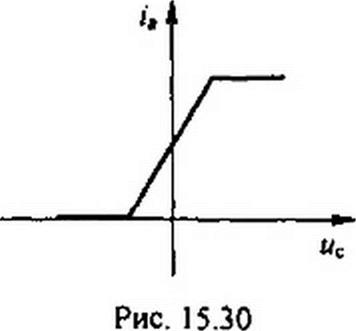4 = 4о ⁺ ^^uc

где /_а0 — значение тока /_а при «_с=0; а(А-В'^х) и Ь{А ■ В^-3) — числовые коэффициенты.

Для определения коэффициентов а и Ь следует выбрать на характеристике две точки с координатами (/_al,w_c)) и (4з» ^и решить систему двух уравнений с двумя неизве­стными:

Характеристика по типу пунктирной кривой на рис. 15.28, б может быть приближен­но описана полиномом пятой степени:

4 =4о ⁺ P^uc ^+<7^uc "''«с-

где р, г и q — числовые коэффициенты.

Как упоминалось, анодный ток /_а является функцией не только анодного, но и сеточ­ного напряжения: 4 - I» Если по отношению к некоторому исходному состоянию (С/_а,У_с) сеточное напряжение получит небольшое приращение Лц_с, то оно вызовет при­ращение анодного напряжения Ди_а и анодного тока Д/_а.

Проделав выкладки, аналогичные выкладкам § 15.32, получим

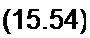△4 -gi ^Дуа +5 Дй_с,

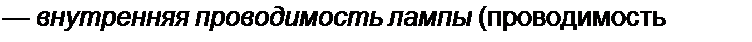д/, гае g,= —

катодом).

Величину, обратную g,, называют внутренним сопротивлением лампы (сопротивле­ние между анодом и катодом):

/?,=—• (15.55)

Si

Крутизна характеристики лампы 5 имеет размерность проводимости:

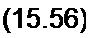£4]

^ди с '(J_a.U_?

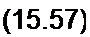Проводимость g, и крутизна характеристики S зависят от вида характеристик лампы и исходных напряжений U_a и U_c. Отношение 5 к g, называют коэффициентом усиле­ния лампы:

И = Slgi-

Коэффициент ц показывает, во сколько раз приращение напряжения между сеткой и катодом Дм_с оказывается более эффективным, чем приращение напряжения между ано­дом и катодом Дп_а в отношении получения одинакового приращения анодного тока Д/_а. С учетом сказанного имеем

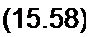Д«_а = Я, Д/, -р Д«_с.

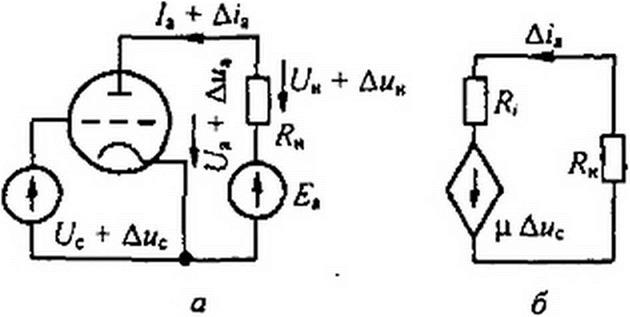
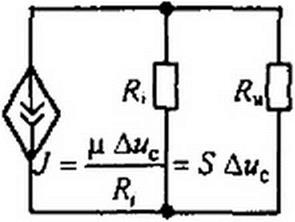
§ 15.40 Схема замещения электронной лампы для малых приращений. На схеме (рис. 15.31, а) через (7_а, U_c, обозначены постоянные составляющие напряже­ний и тока, соответствующие исходному состоянию схемы. Положительные направления для приращений Дм_с, Дм,, Д/, те же, что и для исходных напряжений и токов.

Запишем уравнение для приращений напряжений в анодной цепи, вызванных прира­щением напряжения Дм_с на сетке лампы. С этой целью составим два уравнения по вто­рому закону Кирхгофа для анодной цепи. Одно из них — для режима до получения при­ращений:

U_a +U_H = E;

другое — для режима после получения приращений:

+ Дм. + + Д£Л ~ Е.

а Л п П

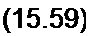Если в последнем уравнении U_a +U_H заменить на Е, то окажется, что

Дм, + Дм_к = О,

где Дм_н — приращение напряжения на нагрузке /?_и.

В уравнение (15.59) вместо Ди_и подставим Л_н Д/_а я вместо Ди_а в соответствии с уравнением (15.58) Я/Д^-рДм,.. В результате получим

(2?_н + /?,)Д/_а = н Ди_с. (15.60)

Уравнению (15.60) отвечает схема на рис. 15.31, б. В этой схеме к управляемому ис­точнику ЭДС рДи_с присоединены нагрузка Я_н и внутреннее сопротивление электрон­ной лампы /?,. Таким образом, для малых приращений анодную цепь электронной лампы замещают (имитируют) источником ЭДС ц Дп_с и последовательно с ним включенным ре­зистором сопротивлением Л,. ЭДС этого источника пропорциональна изменению напря­жения на сетке лампы (т. е. это зависимый источник ЭДС; ср. с § 15.35).

На рис. 15.31, в изображена другая часто используемая схема замещения. В ней вмес­то источника ЭДС включены управляемый источник тока 5 Д«_с и шунтирующий его ре­зистор /?, (напомним, что переход от источника ЭДС к источнику тока рассмотрен в § 2.2).

В схемах на рис. 15.31, б. в не учтены межэлектродные емкости, поэтому такие схемы применимы для относительно низких частот. Схема замещения для высоких частот изоб­ражена на рис. 9.3, б.

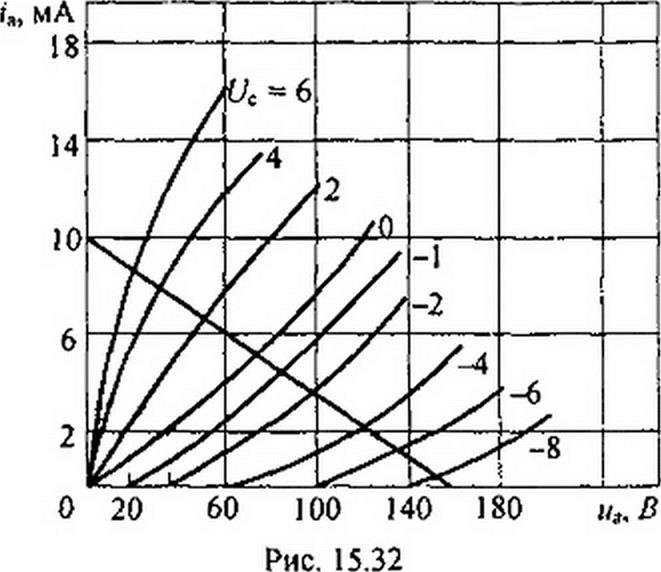
Пример 154. Между сетхой и катодом триода 6С2С приложено напряжение U_c + Ди_с = U_e + 1^ sin со/ = -2+ 0,05 sin ей (рис. 15.31. а). Зависимость i_a = /(u_a) при параметре и_с изображена на рис. 15.32, где Е_а=150В; /?_н=15кОм. Найти параметры схемы замещения триода и определить с помощью этой схемы амплитуду синусоидаль­ной составляющей тока в анодной цели.

Решение. Определим положе­ние рабочей точки на характеристиках лампы по постоянному току. На рис. 15.32 наносим прямую, характе­

ризующую нагрузочное сопротивле­ние анодной цепи. Ее часто называют нагрузочной прямой. Прямая прохо­дит через точки /_а =0, и_а = 150 В и /_а = £_а / /?„ = 10 мА; м_а = 0.

Рабочей точкой в рассмотренном режиме будет точка пересечения пря­мой с той кривой семейства, для ко­торой параметр U_c = -2 В. Координа­ты этой точки: w_a=94B; /_а - 3,67 мА.

По определению (см. форму­лу (15.4)), для нахождения g, следу­ет, считая за исходное положение най­денную рабочую точку, при неизмен­ном U_c = -2 В даггь приращение анодному напряжению Д«_а, найти соответствующее ему приращение анодного тока Д/_а и разделить Д/_а на Д«_а:

dr. &L 5 мА ,,,-4^ ,, । ,_п4г>

g, =—— *—2- =--------------- = 10 См; Rj- — = 10 Ом.

' <Э«_а Д«_а 50 В ' g,

Проводимость gf пропорциональна тангенсу угла наклона касательной в рабочей точке к кривой /_а = /(w_a), для которой = -2 В.

Для определения крутизны характеристики S при «_а = 94 В даем приращение сеточ­ному напряжению Ди_с = -1 - (-2) = 1 В и из рисунка находим соответствующее ему при­ращение Д/_а = 4,67 - 3,67 = I мА. Следовательно, S~di_a! du_z * Л/_г/ Ди_с = 10’³ А / В. Коэффициент усиления n = S/g, =10. Амплитуда синусоидальной составляющей тока в анодной цепи, согласно (15.60),

/ - ±^_ ₌ 2 lO'^s А.

+ R.

Анодный ток /_а = 3,67 + 0.02 sin о t мА.

§ 15.41 Тиристор — управляемый полупроводниковый диод. На рис. 15.33, а изображена простейшая схема включения тиристора. Тиристор — это четырехслойный полупроводниковый прибор с тремя

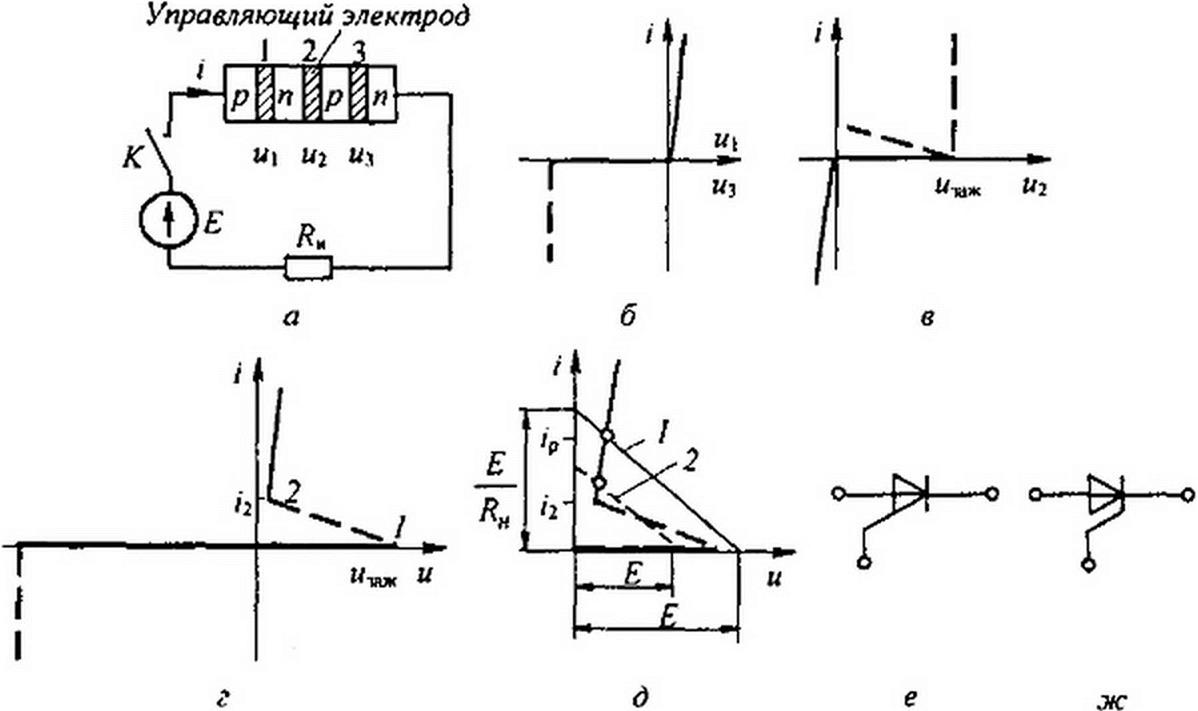
Рис. 15.33

р—//-переходами (7, 2, 3). Напряжения на них обозначены и₂, ы₃, ВАХ р—«-переходов 7 и 3 изображены на рис. 15.32, б, ВАХ перехода 2 — на рис. 15.33, в (включен встречно р—/7-переходам 7 и 3). При и₂ = и^ в переходе 2 происходит лавинная ионизация (штриховая линия на рис. 15.33, в). Суммарная ВАХ трех переходов 7 = /(и), т. е. ВАХ всего тиристора, изображена на рис. 15.33, г. Она получена сложением абсцисс (рис. 15.33, в) и двух абсцисс (рис. 15.33, б). Участок 7—2 на ней соот­ветствует участку лавинной ионизации второго р—//-перехода.

Если при замкнутом ключе К (см. рис. 15.33, а) ЭДС Е станет немного больше и_заж, тиристор зажжется, т. е. перейдет в открытое состояние. Ток в цепи станет равным току ip на рис, 15.33, д. Прямую 7 (рис. 15.33, б) называют нагрузочной. Для погашения тиристора необхо­димо, чтобы ток через него уменьшился до i<i₂ (рис, 15.33, г). До сих пор рассматривалась работа тиристора при отсутствии управляющего сигнала (так работает динистор). При воздействии управляющего сигна­ла (импульса тока или напряжения) на управляющий электрод (располо­женный вблизи р—«-перехода 2 на рис. 15.33, а) от вспомогательной цепи, не показанной на рис. 15.33, а, происходит лавинная ионизация р— /7-перехода 2. Подавая импульсы управления, можно снижать напряже­ние зажигания (т. е. зажигать прибор при более низком н_мж).

Штриховой линией на рис. 15.33, д показано положение нагрузочной прямой 2 в управляемом тиристоре. Переход от закрытого состояния к открытому происходит за доли микросекунды. Тиристоры выполняют на токи от долей миллиампер до нескольких килоампер. На рис. 15.33, <?, ж показано условное изображение тиристора на схемах: рис. 15.33, е соот­ветствует управлению тиристором со стороны анода, рис. 15.33, ж— со стороны катода.

§ 15.42 Общая характеристика методов анализа и расчета нели­нейных электрических цепей переменного тока. Анализ нелинейных явлений и получение числовых соотношений в нелинейных цепях пере­менного тока являются более сложным и трудоемким, чем анализ и рас­чет линейных электрических цепей.

Как правило, в нелинейных электрических цепях содержатся либо нелинейные индуктивности, либо нелинейные конденсаторы, либо безынерционные в тепловом отношении нелинейные резисторы. Токи и напряжения в таких цепях в той или иной степени несинусоидальны.

Токи и напряжения в большей степени синусоидальны в цепях, содержащих только инерционные в тепловом отношении нелинейные ре­зисторы.

Все методы анализа нелинейных цепей можно разделить на две боль­шие группы: аналитическую и графическую. Аналитические методы в отличие от графических дают возможность проводить анализ в общем виде, а не только для частных значений параметров.

Недостатком аналитических методов является то, что приходится выражать аналитически характеристики нелинейных элементов, а это всегда связано с некоторой погрешностью. Расчет сколько-нибудь слож­ных нелинейных электрических цепей переменного тока можно провес­ти лишь с известной степенью приближения.

Наиболее широко распространены следующие методы анализа и рас­чета нелинейных цепей переменного тока:

1) графический при использовании характеристик нелинейных элемен­тов для мгновенных значений;

2) аналитический при использовании характеристик нелинейных эле­ментов для мгновенных значений при их кусочно-линейной аппроксима­ции;

3) аналитический или графический при использовании ВАХ по пер­вым гармоникам;

4) аналитический или графический при использовании ВАХ по дей­ствующим значениям несинусоидальных величин;

5) аналитический путем расчета по первой и одной или нескольким высшим или низшим гармоникам;

6) с помощью линейных схем замещения;

7) малого параметра;

8) интегральных уравнений;

9) моделирования.

В дальнейшем кратко охарактеризован каждый метод. Тот или иной метод целесообразно применять в зависимости от числа нелинейных элементов, формы их характеристик, а также от того, какое нелинейное явление в цепи исследуется. Чем сложнее характер нелинейного явления, тем более сложным и громоздким оказывается метод его анализа. И на­оборот, анализ грубых нелинейных явлений выполняется простыми сред­ствами.

§ 15.43 Графический метод расчета при использовании характе­ристик нелинейных элементов для мгновенных значений. Этот ме­тод применим, как правило, к цепям, в которых известен закон измене­ния во время какой-либо одной определяющей работу нелинейного эле­мента величины, например тока, напряжения, заряда.

Последовательность расчета данным методом такова:

1) исходя из физических предпосылок, положенных в основу анали­за, считают известным закон изменения во времени одной из определя­ющих работу нелинейного элемента величины;

2) используя характеристики (характеристику) нелинейного элемента для мгновенных значений, путем графических построений находят закон изменения во времени второй величины, определяющей работу нелиней­ного элемента;

3) по результатам п. 2 путем вспомогательных графических построе­ний и простейших расчетов определяют выходную величину и искомое соотношение между параметрами схемы.

Достоинствами метода являются простота и наглядность, а также лег­кость учета гистерезисных явлений. Примеры см. в § 15.8 и 15.24.

§ 15.44 Аналитический метод расчета при использовании харак­теристик нелинейных элементов для мгновенных значений при их кусочно-линейной аппроксимации. Основой метода является сведение задачи о нахождении периодического решения нелинейных уравнений к определению периодического решения системы линейных уравнений.

Основные этапы метода следующие:

1) замена вольт-амперной (вебер-амперной, кулон-вольтной) характе­ристики нелинейного элемента для мгновенных значений отрезками пря­мых линий;

2) подстановка в нелинейные дифференциальные уравнения уравне­ний прямых п. 1 (этим нелинейные дифференциальные уравнения будут сведены к линейным). Каждому нелинейному уравнению будет соответ­ствовать столько линейных уравнений, сколько отрезков прямых заменя­ют характеристику нелинейного элемента;

3) решение системы линейных дифференциальных уравнений. Каж­дому линейному участку характеристики нелинейного элемента будет соответствовать свое решение со своими постоянными интегрирования;

4) определение постоянных интегрирования исходя из согласования решения на одном линейном участке с решением на другом линейном участке.

Наиболее эффективен этот метод, когда характеристику нелинейного элемента с известной степенью приближения можно заменить отрезка­ми прямых, расположенных таким образом, что когда одна величина, определяющая режим работы нелинейного элемента, например ток, ме­няется, то другая, например потокосцепление, неизменна.

Еще более эффективен метод, если отрезки прямых, заменяющие ВАХ нелинейного элемента, могут быть взяты совпадающими с осями коор­динат. Пример решения задачи для этого случая см. в § 15.51-15.53.

§ 15.45, Аналитический (графический) метод расчета по первым гармоникам токов и напряжений. В этом методе по сложному закону изменяющиеся токи и напряжения на нелинейном элементе заменяют их первыми гармониками. В расчете используют ВАХ по первым гармони­кам в аналитической форме или в виде графической зависимости.

Основные этапы расчета в аналитическом варианте:

1) выражают аналитически ВАХ нелинейного элемента для мгновен­ных значений;

2) путем подстановки в нее первой гармоники напряжения или тока получают формулу, которая дает нелинейную связь между амплитудой первой гармоники тока через нелинейный элемент и амплитудой первой гармоники напряжения на нем (в качестве примера такой связи можно назвать формулу (15.19));

3) в уравнение, составленное для исследуемой цепи по второму зако­ну Кирхгофа, подставляют вместо мгновенных значений тока и напря­жения на нелинейном элементе мгновенные значения их первых гармо­ник, а высшими гармониками пренебрегают;

4) уравнение разбивают на два уравнения: одно из них выражает со­бой равенство коэффициентов при синусных слагаемых левой и правой частей уравнения, другое — равенство коэффициентов при косинусных слагаемых обеих частей уравнения;

5) совместно решают эти два уравнения.

Основные этапы расчета в графическом варианте:

1) в качестве зависимости между амплитудой первой гармоники на­пряжения на нелинейном элементе и амплитудой первой гармоники тока через него берется нелинейная зависимость в виде графика. Эта зависи­мость может быть получена любым путем, в том числе и опытным;

2) произвольно задаются амплитудой /_1ш первой гармоники тока через нелинейный элемент, из графика находят соответствующую ей амплитуду первой гармоники напряжения на нем и затем путем по­строения векторной диаграммы по первой гармонике для всей схемы определяют амплитуду U_lm первой гармоники напряжения на входе схемы. Векторная диаграмма строится так же, как и для обычных линейных цепей синусоидального тока, а именно: если не учитывать потери в сердечнике, то первая гармоника напряжения на нелинейной индуктивной катушке опережает первую гармонику протекающего через нее тока на 90°, первая гармоника напряжения на нелинейном кон­денсаторе отстает от протекающего через него тока на 90°, первые гармоники напряжения и тока на нелинейном резисторе по фазе совпа­дают;

3) построением нескольких векторных диаграмм для различных зна­чений /_1т находят соответствующие им U_ln, и строят ВАХ всей схемы

Данный метод позволяет рассматривать такие нелинейные явления, как преобразование постоянного тока в переменный и обратное преоб­разование, явление резонанса на основной гармонике, триггерный эффект на первой гармонике, некоторые типы автомодуляционных процессов. Но он не позволяет исследовать более сложные явления, как, например, ре­зонанс на высших, низших или дробных гармониках и др.

Если пользоваться аналитическим вариантом этого метода, то реше­ние можно получить в общем виде, что существенно, так как становится возможным исследовать решение при изменении любого из параметров цепи. Этот метод будет применен для анализа работы автогенератора (см. § 15.56) и для анализа работы разветвленной цепи с нелинейной индуктивной катушкой (см. пример 159).

§ 15.46. Анализ нелинейных цепей переменного тока с использо­ванием ВАХ для действующих значений. В этом случае графический расчет проводят с помощью ВАХ нелинейных элементов для действую­щих значений, полученных расчетным или опытным путем.

При этом полагают, что в действительности несинусоидально изме­няющиеся токи и напряжения могут быть заменены эквивалентными им синусоидальными величинами (эквивалентность в смысле действующе­го значения).

Все этапы расчета рассматриваемым методом полностью совпадают с перечисленными в § 15.45 этапами графического расчета методом пер­вой гармоники. Отличие между методами состоит только в том, что в данном случае используется ВАХ не для первых гармоник, а для действу­ющих значений.

Метод применен в дальнейшем для исследования простейших явле­ний в феррорезонансных цепях (см. § 15.57-15.62).

Если исследуют нерезонансные электрические цепи или резонансные, но для которых по тем или иным соображениям заранее известно, что в изучаемых режимах работы в них не могут возникать резонансные явле­ния на высших и низших гармониках, то амплитуда первой гармоники тока, как правило, оказывается больше амплитуд высших гармоник тока. При этом действующее значение тока в цепи сравнительно мало отлича­ется от действующего значения первой гармоники тока.

Чтобы убедиться в этом, рассмотрим следующий пример: пусть ток в цепи содержит первую и третью гармоники и действующее значение тре­тьей гармоники тока составляет 40 % действующего значения первой гармоники (/₃ =0,4 /,). Действующее значение несинусоидального тока будет у]/² + Ц _ 1Q75 / т. е. всего на 7,5 % больше действующего зна­чения первой гармоники

Метод позволяет изучать некоторые свойства нерезонансных электри­ческих цепей, как, например, эффект усиления мощности. Для исследо­вания свойств резонансных нелинейных цепей метод пригоден в ограни­ченной степени. Так, им можно приближенно исследовать простейший триггерный эффект (см. § 15.59), но нельзя, например, исследовать ре­зонансные явления на высших гармониках.

Рассмотрим, как можно получить аналитическое выражение ВАХ не­линейного элемента по действующим значениям величин с учетом выс­ших гармоник при описании характеристики для мгновенных значений функцией у - a sh (3 х и когда под х = х_т sin w t будем понимать напря­жение на нелинейном элементе, а поду — ток через него. Действующее значение х равно х_т / ^2, а действующее значение функции у по опре­делению подсчитаем по формуле

2 п

Jsh^{[7] [8] [9]} р х_т sin со t dсо t. о

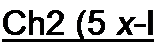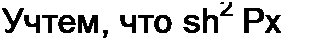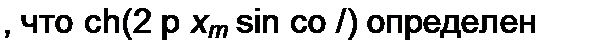мулой (15.10), если аргумент бесселевых функций в ней удвоить. При­мем во внимание также, что интеграл от всех косинусоидальных функ­ций в ней за период первой гармонии равен нулю. Получим формулу

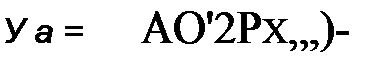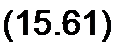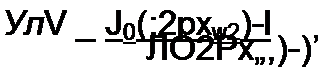Если опытным путем снять ВАХ нелинейного элемента по действую­щим значениям и учесть, что аналитически она описана формулой (15.61), то по двум точкам ее (пусть координаты их х, =х_т1 /^2 и у_Д| и х₂=х_и2/^ и у_д2) можно определить коэффициенты аир в формуле аналитического описания характеристики НЭ y = ashpx для мгновен­ных значений. Действительно, коэффициент р может быть определен из

Расчет этим методом, как правило, громоздок. Однако метод позволяет исследовать такие сложные явления в нелинейных цепях, как резонанс на высших, низших и дробных гармониках. Метод рассмотрен в § П9.4.

Рассматриваемый метод в литературе называют также методом гармонического ба­ланса. Частным случаем его является метод первой гармоники (см. § £5.47).

§ 15.48 Расчет цепей с помощью линейных схем замещения. Этот метод приме­ним к расчету нелинейных электрических цепей, на которые воздействуют постоянные и синусоидально изменяющиеся ЭДС, если переменные составляющие токов и напряжений относительно малы, например во много раз меньше соответственно постоянных состав­ляющих токов и напряжений.

Последовательность расчета такова:

1) определяют положение рабочей точки на характеристике нелинейного элемента по постоянному току. В окрестности этой точки будет перемешаться изображающая точка под воздействием малой переменной ЭДС;

2) через рабочую точку по постоянному току проводят касательную к характеристике нелинейного элемента и производят замену участка его характеристики отрезком касатель­ной;

3) составляют линейную схему замещения для расчета переменной составляющей. Вид схемы зависит от характера нелинейного элемента, а ее параметры — от тангенса угла, составленного касательной к характеристике и одной из осей координат.

ЭВМ применяют для:

§ 1.1 улирования решений систем трансцендентных уравнений и систем алгебраиче­ских уравнений высоких степеней;

§ 1.2 улирования решений, выраженных в виде медленно сходящихся рядов;

§ 1.3 егрирования систем линейных дифференциальных уравнений, к которым сводят­ся нелинейные дифференциальные уравнения при кусочно-линейной аппроксимации ха­рактеристик нелинейных элементов;

§ 1.4 ленного интегрирования нелинейных дифференциальных уравнений, в которых ВАХ нелинейных элементов представлены аналитически, а также в некоторых других слу­чаях.

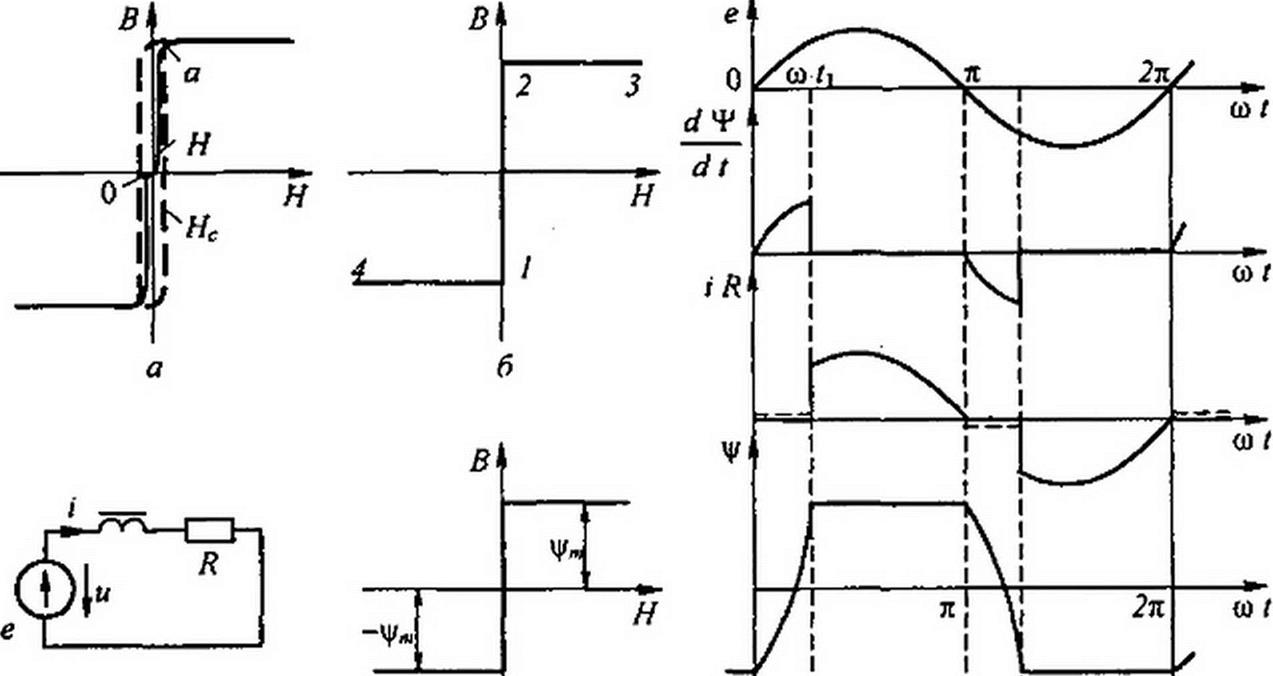
§ 15.49 Расчет цепей, содержащих индуктивные катушки, сердеч­ники которых имеют почти прямоугольную кривую намагничива­ния. Кривые намагничивания некоторых высококачественных магнито­мягких материалов, например 65НП, 68НМП и др., близки по форме к прямоугольной: на участке 0—а (рис. 15.34, а) кривая почти совпадает с осью ординат, а на участке а— b расположена почти параллельно оси абсцисс.

На рис. 15.34, а штриховой линией показана предельная петля гисте­резиса. Коэрцитивная сила Я_с для таких материалов очень мала и составляет 1-10 А/м.

Расчет электрических цепей переменного тока, содержащих индуктив­ности, сердечники которых выполнены из упомянутых магнитных мате­риалов, обычно производят с помощью метода кусочно-линейной аппроксимации (см. пример 155). Для облегчения расчета кривую намаг­ничивания заменяют идеально прямоугольной (рис. 15.34, б). Участки 4—1 и 2—3 параллельны оси абсцисс, а участок 1—2 совпадает с осью ординат.

Если изображающая точка перемещается по участку /—2, то изме­няется только индукция в сердечнике при напряженности поля в сердеч­нике, почти равной нулю. При движении изображающей точки по участ­кам 4—1 и 2—3 меняется только напряженность поля Н, а индукция в

в г д

Рис. 15.34

сердечнике остается неизменной.

Пример 155. Схема (рис. 15.34, в) состоит из источника синусоидальной ЭДС е = Е_т sin со/, индуктивности с заданной зависимостью потокосцепления V от тока i и

резистора сопротивлением R. Вывести формулу для определения Ч* и i и построить гра­фики изменения ф и i во времени в установившемся режиме.

Решение. Так как потокосцепление V равно произведению индукции в сердеч­нике В на площадь поперечного сечения сердечника и на число витков обмотки: ку = В S и\ а по закону полного тока ток i ~ Н Uw, т. е. пропорционален напряженности магнитного поля в сердечнике, то зависимость потокосцепления оттока г (рис. 15.34, г) качественно такая же, как и зависимость В = f(H) (рис. 15.34,6). Имеем

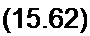d\u

——+ /?/= £_ sin соt. dt

В интервале времени от со t - 0 до со/ = оГ| (назовем его первым) ток / = 0, все напряжение приходится на индуктивную катушку dyldt = Е_т sin со t и потокосцепление V изменяется от до (изображающая точка на рис. 15.34,6 перемещается от / к 2).

В этом интервале dy = Е„, sin со/ dt\ следовательно,

V = - -^2- cos со t + С, (15.63)

О)

где С — постоянная интегрирования.

Во втором интервале времени от соI = со/| до со/ = л потокосцепление V остается постоянным и равным dyfdi = 0; из уравнения (15.62) получим

£

R i = Е_т since /, или / = —— sinew. (15.64)

R

Таким образом, во втором интервале времени ток / изменяется по закону синуса, по­токосцепление V постоянно и равно V„,. При этом изображающая точка перемещается по участку 2—3 (рис. 15.34, 6).

Найдем постоянную интегрирования С и значение Для определения С запишем уравнение (15.63) при <ог = 0. Для этого момента времени = поэтому -\р_т = Е_т /со + С. Отсюда С = -ц*_т + Е_т / <о.

Для нахождения w q воспользуемся также уравнением (15.63), учтя, что при wz = о/| V = V_m. Получим

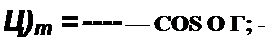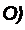Отсюда

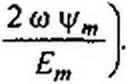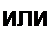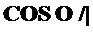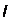Характер изменения тока/, потокосцепления ц» и d^ldt, когда о> у „,/£„< I, по­казан на рис. 15.34, д.

Если амплитуда ЭДС Е_т < to то второго интервала времени не возникнет, т. е. ток i - 0 в течение всего периода.

Отметим, что если учитывать гистерезис, то перемагничивание сердечника будет про­исходить при токе /*0. При dyldt>$ i = i_c, при dxy/di<0 i = -i_e (см. пунктир на рис. 15.34, д). Ток /_с соответствует коэрцитивной силе Н_с (см. рис, 15.34, а).

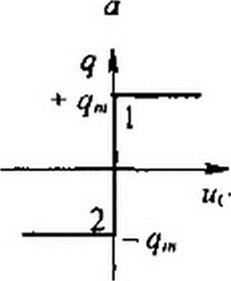
§ 15.50 Расчет цепей, содержащих нелинейные конденсаторы с прямоугольной кулон-вольтной характеристикой. Метод расчета рас­смотрим на примере цепи (рис. 15.35, а), которая состоит из источника синусоидальной ЭДС е = Е_п, sin со/, нелинейного конденсатора с почти прямоугольной кулон-вольтной характеристикой (рис. 15.35, б) и резис­тора сопротивлением R. Задача эта близка рассмотренной в § 15.49. По второму закону Кирхгофа и_с + R — = е. При перезарядке конденсато- dt

ра изображающая точка движется по участку 2—/ характеристики q = f(^uc^ при этом и₍- =0. Когда перезарядка закончится, все напряже­ние источника окажется приложенным к конденсатору. При 1=0 q = ~q_m. Во время перезарядки, когда и_с =0,

dq ЕЕ

R — - Е_т sin со t\ q------------ — cos co t - q_m + ——.

dt ^m uR ®R

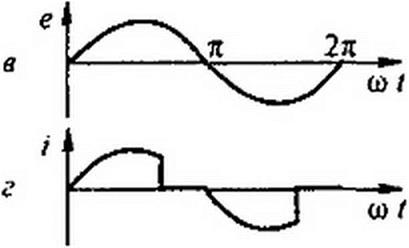
К концу перезарядки при <d q достигает значения q_m',

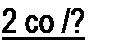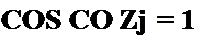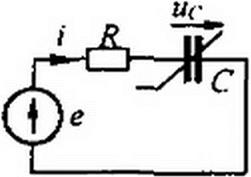
В интервале времени от со /j до п и_с = Е_т sin со Z.

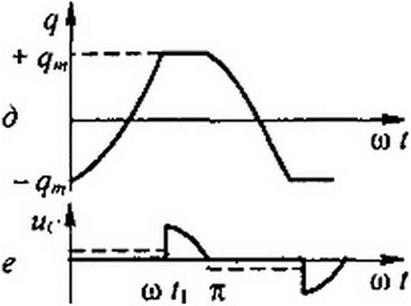
Графики z, q, uq изображены на рис. 15.35.

Если учесть гистерезис (см. рис. 15.35), то перезарядка конденсатора происходит при напряжении на нем, немного не равном нулю (см. шт­риховая линия на рис. 15.35, г, д, е).

§ 15.51 Выпрямление переменного напряжения. Под выпрямлением переменного напряжения понимают процесс преобразования переменно­го напряжения в постоянное или пульсирующее. Выпрямление произво­дят с помощью полупроводниковых, ламповых или других типов диодов.

Неуправляемый диод изображают на схемах в виде большой треуголь­ной стрелки с поперечной чертой у острия. Стрелка показывает прово­дящее направление. Сопротивление диода в проводящем направлении в тысячи раз меньше, чем в непроводящем.

По числу фаз выпрямленного переменного напряжения выпрямитель­ные схемы делят на одно- и многофазные. Однофазные схемы подразде­ляют на схемы одно- и двухполупериодного выпрямления.

В однополупериодных схемах выпрямление производится, грубо говоря, в течение одного полупериода питающего напряжения, в двух- полупериодных — в течение обоих полупериодов.

Мостовая схема однофазного двухполупериодного выпрямления пред­ставлена на рис. 15.36, а. Она состоит из четырех полупроводниковых диодов (/, 2, 3 и 4), источника выпрямляемого синусоидального напря­жения e(Z) и нагрузки R_H. На рис. 15.36, в показаны положительные направления тока i и напряжения и_Л на диоде.

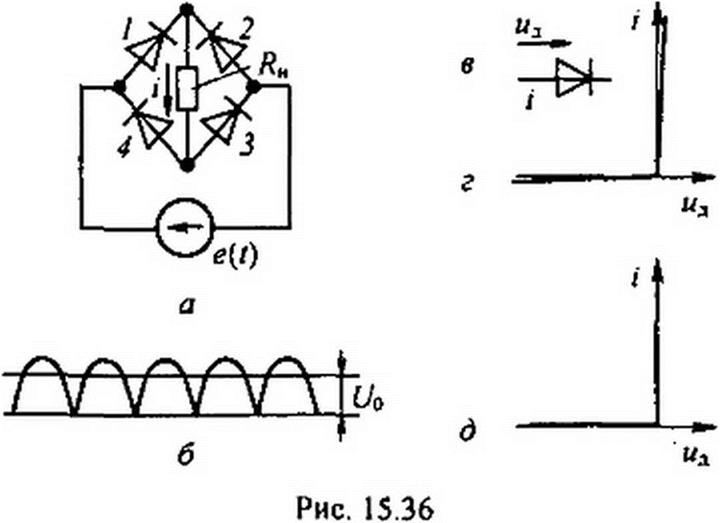На рис. 15.36, г изображена ВАХ диода. В целях облегчения анализа вместо нее будем пользоваться идеализированной ВАХ, изображенной на рис. 15.36, д.

В соответствии с этой идеализированной характеристикой, когда че­рез диод проходит ток, падение напряжения на нем равно нулю и, следо­вательно, сопротивление самого диода равно нулю. Когда напряжение на диоде отрицательно (т. е. отрицательна взятая в направлении стрелки рис. 15.36, в разность потенциалов на самом диоде), диод не проводит тока (7 - 0) и сопротивление его равно бесконечности.