§ 15.17 Некоторые общие свойства симметричных нелинейных элементов.

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Если нелинейный элемент с симметричной характеристикой работает в условиях, когда одна из определяющих его состояние величин, например величинах, изменяется во времени по закону х = х₀ + х„, sin coz, то в отношении другой определяющей его состоя­
ние величины (величины у) можно сделать следующие выводы:

1) постоянная составляющая функции у₀ зависит не только от л₀, но и от х„, что следует из (15.12);

2) в кривой у = /(со г) появляются четные гармоники, которые исчезают при х₀ =0. Фаза четных гармоник зависит от знака постоянной составляющей (от знака х₀);

3) путем изменения х₀ или y_Q можно изменять амплитуды первой и высших гармо­ник функций.

а б

Рис. 15.14

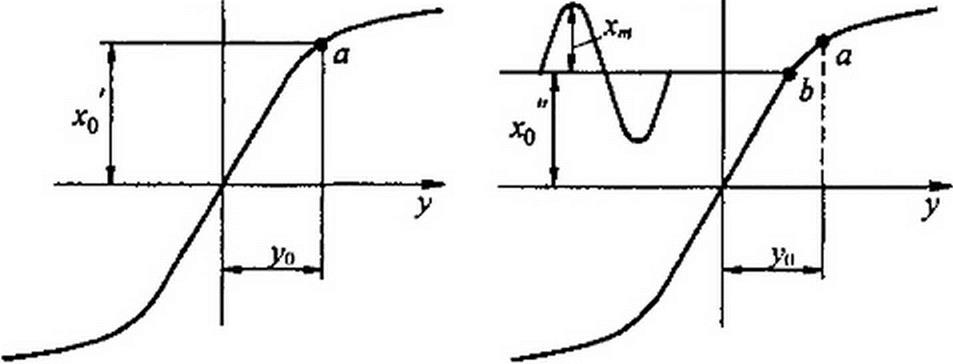
Первое из этих свойств поясним графически. Пусть нелинейный элемент работает при отсутствии синусоидальной составляющей (х_Л| =0). Тогда изображением этого процесса на характеристике нелинейного элемента будет точка а (рис. 15.14, а}. Для нее

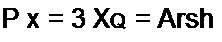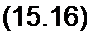Этот результат следует из (15.12), если учесть, что J_o(O) = 1.

Если же нелинейный элемент работает при х_т * 0, то, для того чтобы постоянную составляющую функции у₀ сохранить прежней, постоянная составляющая х₀ должна быть снижена (или снизится сама) со значения х'_о до Xq.

Постоянная составляющая где Xq определяется ординатой точки Ь. расположенной ниже точки а (рис. 15.14, б).

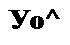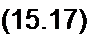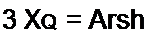Первое и третье из этих свойств широко используют в теории управляемых нелиней­ных элементов, второе свойство — в теории умножителей и делителей частоты.

Пример 150. Нелинейный элемент с характеристикой у = a sh 0 х сначала работал при у₀/а - 41,1 и отсутствии переменной составляющей (3 х_т - 0). Затем режим работы его изменился: постоянная составляющая у$!а осталась прежней, но появилась переменная составляющая 3*> амплитуда которой 3*т=⁴- Найти постоянные составляющие Рх₀ в этих двух режимах.

Решение. В первом режиме 0 — Arsh 4 М — 41,1. Во втором режиме 3 хо = Arsh(41,1 / J₀(j 4)) = Arsh 3,63 = 2.

Таким образом, при переходе от первого режима ко второму постоянная составляю­щая 3 *о изменилась с 4,41 до 2. т. е. более чем в два раза.

II. В энергетическом отношении общие свойства нелинейной цепи, содержащей одну нелинейную катушку (конденсатор) с безгистерезисной симметричной характеристикой, в которой действуют генераторы синусоидальных колебаний с частотами /, и /₂ и воз­никают токи и напряжения частот f_m,„ -т f_}+n f₂ (тип — простые числа, принимаю­щие положительные, отрицательные и нулевые значения), для периодических процессов описываются теоремой Мэнли и Роу.

Если через IV_m„ =U_mll + обозначить среднюю за период мощность,

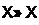
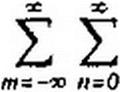
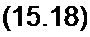поступающую в нелинейную индуктивную катушку (конденсатор) на частоте fm.n ^{= m} f\⁺ⁿ /2» то теорема устанавливает связь между мощностями, поступающими в нелинейный элемент на различных частотах. Эту теорему записывают в виде двух соот­ношений (доказательство см., например, в [24]):

/7? ИС »

/Л ,7г

«/l +rt/₂

§ 15.18 Появление постоянной составляющей тока (напряжения, потока, заря­да) на нелинейном элементе с симметричной характеристикой. Если к нелинейному резистору с симметричной ВАХ, например i = ait, подвести напряжение в виде двух компонент 1/ = Ц sin<of + C'₂ sin(2 ©/ + <₽), частоты которых относятся как 1:2 (в более общем случае как 2 к /(2 р +1). где к и р — целые положительные числа), то в токе, про­ходящем через HP, несмотря на отсутствие выпрямите/тей, появится постоянная составля­ющая, равная -0,75a (/j² (Л sintp. Ее значение зависит не только от U_x и U₂> но и от угла Ф- Сам факт возникновения постоянной составляющей в этих условиях называют селективным выпрямлением. Селективно оно потому, что возникает не при любом соот­ношении частот двух напряжений, а при вполне определенном. Сходное явление имеет место в нелинейных индуктивных катушках и конденсаторах. Так, если на нелинейную индуктивную катушку с ВАХ / = а$ЬрФ воздействовать потоками частот о и 2а, то при отсутствии постоянной составляющей в МДС в потоке кроме указанных гармоник появится и постоянная составляющая. Для ее определения положим Ф х Ф_о + Ф] sin(w / + <р) + Ф_: sin 2 <о г, подставим в формулу для тока и, разложив ток в ряд Фурье, приравняем постоянную составляющую тока нулю. 0 результате получим форму­лу для определения Ф_о:

_{dl v}

J<> (J ь,) (jь₂ )

где b₀ = рФ₀: b₂ = рФ₂-

Если через нелинейный конденсатор проходят первая и вторая гармоники тока, а угол Ф # 0, то на нем будет постоянная составляющая заряда при отсутствии постоянной со­ставляющей напряжения.

§ 15.19 Типы характеристик нелинейных элементов. При анали­зе и расчете электрических цепей с нелинейными элементами в зависи­мости от рассматриваемого вопроса используют различные типы ха­рактеристик одного и того же нелинейного элемента:

а) характеристики для мгновенных значений;

б) ВАХ по первым гармоникам тока и напряжения;

в) ВАХ для действующих значений.

§ 15.20 Характеристики для мгновенных значений. Основным типом характеристик являются характеристики, связывающие мгновен­ные значения основных определяющих величин: тока и напряжения на нелинейном резисторе, индукции и напряженности в сердечнике нели­нейной индуктивности, заряда и напряжения на нелинейном конденса­торе. Будем называть их характеристиками для мгновенных значений. Иногда перед этим названием добавляют, соответственно, следующие слова: вольт-амперные, вебер-амперные или кулон-вольтные. В силу ряда причин, обусловленных различными физическими процессами в самих нелинейных элементах, форма характеристик меняется с увеличением скорости изменения определяющих величин во времени.

§ 15.21 ВАХ по первым гармоникам. Под ВАХ по первым гармо­никам понимают графическую или аналитическую связь между ампли­тудой (действующим значением) первой гармоники тока и амплитудой (действующим значением) первой гармоники напряжения на нелинейном элементе.

Этот тип характеристик подразделяют на две подгруппы. В первой подгруппе напряжение (поток или заряд) на нелинейном элементе изме­няется по синусоидальному закону, а во второй по синусоидальному за­кону во времени меняется ток через нелинейный элемент (напряженность в сердечнике нелинейной индуктивной катушки или напряжение на нелинейном конденсаторе).

Если воздействующее на нелинейный элемент синусоидальное напря­жение (синусоидальный ток) не содержит постоянной составляющей, то ВАХ для первых гармоник данного элемента изображают какой-то одной кривой. Если же воздействующее напряжение (ток) содержит постоян­ную составляющую, то вольт-амперные, вебер-амперные или кулон-воль- тные характеристики изображают семействами кривых, на которых по­стоянная составляющая тока, напряжения, потока или заряда является па­раметром.

Этот тип характеристик получают расчетным аналитическим или гра­фическим путем по соответствующим характеристикам для мгновенных значений или снимают экспериментально.

При графическом построении задаются различными значениями ам­плитуды воздействующего на нелинейный элемент напряжения (тока, индукции, заряда), по точкам строят кривую тока (напряженности, напря­жения) в функции времени и путем разложения ее в ряд Фурье находят соответствующие амплитуды первой гармоники тока (напряженности, напряжения). (Пример графического построения кривой тока в функции времени для управляемой нелинейной индуктивной катушки см. на рис. 15.17.)

Аналитически построение точек обсуждаемой характеристики произ­водят. используя формулы (15.12) и (15.13) или иные, подобные им.

В § 15.23 рассмотрено применение формул (15.12) и (15.13) для по­лучения единых характеристик по первым гармоникам для управляемых симметричных нелинейных элементов.

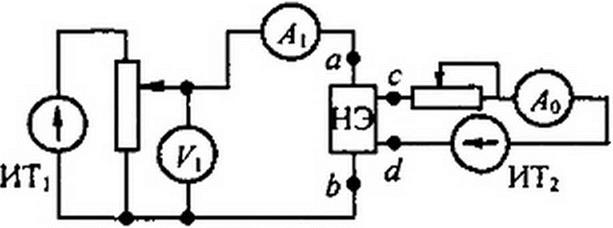
Для нелинейной индуктивной катушки ВАХ по первым гармоникам можно получить опытным путем с помощью схемы рис. 15.15, а, где ИТ_} — источник синусоидальной ЭДС; ИТ₂ — источник постоянной ЭДС; ab — зажимы управляемой цепи НЭ; cd— зажимы управляющей цепи НЭ. Измерительный прибор реагирует на первую гармонику на­пряжения, а измерительный прибор Л, — на первую гармонику тока.

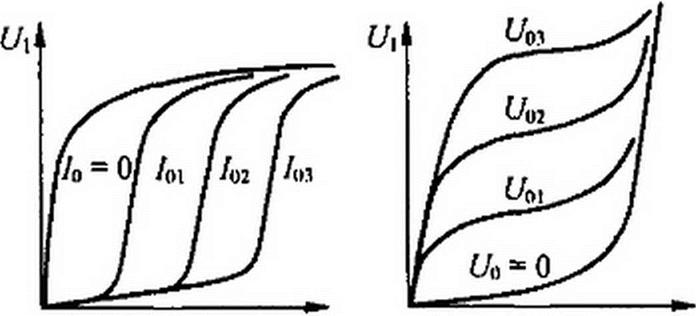
На рис. 15.15,5 качественно изображены ВАХ управляемой нелиней­ной индуктивной катушки по первым гармоникам. Параметром является ток управления /₀. ВАХ по первым гармоникам для управляемого нели­нейного конденсатора изображены на рис. 15.15, в. Параметром являет­ся управляющее постоянное напряжение С/_о.

Снятие характеристик (рис. 15.15, б) производят следующим образом. Устанавливают некоторое произвольное значение тока /₀ в цепи управ­ления, затем плавно повышают напряжение и для каждого его значе-

ния записывают значение тока 1_}. Затем то же проделывают при новом значении /₀ и т. д. Результаты измерений наносят на график и соответ­ствующие точки соединяют плавной кривой.

ВАХ для первых гармоник используют при расчете установившихся режимов в нелинейных цепях, который называют расчетом по пер­вой гармонике (см. § 15.47). При расчете применяют ВАХ той подгруп­пы, которая более подходит по условию работу данного нелинейного элемента.

§ 15.22 ВАХ для действующих значений. Под ВАХ для действую­щих значений понимают зависимость между действующим значением синусоидального (несинусоидального) напряжения на нелинейном эле­менте и действующим значением тока, протекающего через него. Если напряжение (ток) содержит постоянную составляющую, то ВАХ для дей­ствующих значений изображают семейством кривых, на которых посто­янная составляющая тока (потока, напряжения или заряда) является параметром.

Эти характеристики получают графическим или аналитическим пу­тем из характеристик для мгновенных значений или снимают опытным путем с помощью схемы (см. рис. 15.15, а), но приборы V_x и в этом случае должны измерять действующие значения.

ВАХ для действующих значений зависят от формы напряжения на нелинейном элементе и (или) от формы протекающего через него тока, поэтому необходимо указывать, при каких условиях они получены.

При качественном и грубом количественном анализах полагают, что характеристики, снятые при одной форме напряжения на нелинейном элементе, близки к характеристикам, снятым при другой форме напря­жения. В действительности же количественное различие в характерис­тиках может оказаться значительным. ВАХ для действующих значений используют при расчете, называемом расчетом по ВАХ для действующих значений (см. § 15.48).

§ 15.23 Получение аналитическим путем обобщенных характеристик управля­емых нелинейных элементов по первым гармоникам. Как отмечалось, нелинейные индуктивности и конденсаторы, а также большая группа нелинейных резисторов имеют характеристики для мгновенных значений, которые могут быть приближенно описаны формулой у = a sh р х. Для каждого нелинейного элемента под х и у следует понимать свои величины (см. § 15.13).

Таким образом, х и у — обобщенные обозначения величин, определяющих работ)' нелинейного элемента. Для всех перечисленных нелинейных элементов можно построить единые характеристики по первым гармоникам. С этой целью положим х- х₀ +х_т sin о/. Тогда в соответствии с (15.13) амплитуда первой гармоники функции

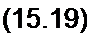У\т = 2 а сАр х₀ (-; (J р х„)).

Формула (15.19) устанавливает связь между амплитудой у_}0, первой гармоники у, амплитудой х„, первой гармоники х и постоянной составляющей х₀.

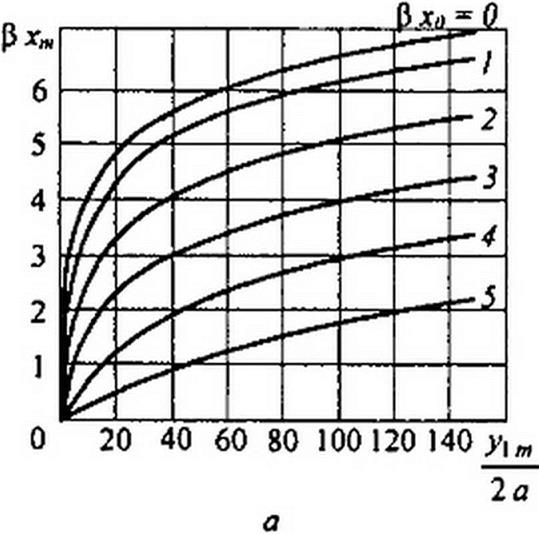
На рис. 15.16, а изображены характеристики управляемого нелинейного элемента 3х_т ~ /(У1_т/2а) при Рх₀ = 0.1,2,3,4,5, построенные по (15.19). Кривыми можно пользоваться при известном значении параметра Рх₀. Если известна не Рх₀, а постоян­

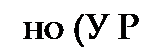ная составляющая у₀/а, то семейство кривых рх„, = /(у_1т /(2 а)) при параметре у₀/а может быть построено следующим образом. Из (15.12) находим shPx₀ = —— _и вместо ch р х₀ в (15.19) подставим

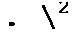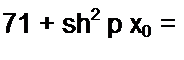В результате получим

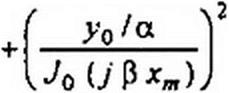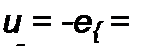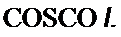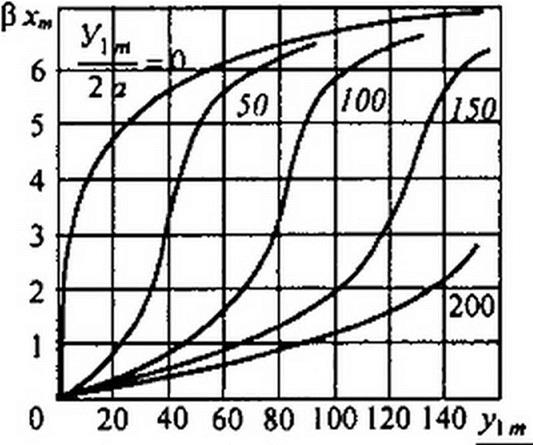
Кривые (см. рис. 15.16, б), построенные по формуле (15.20), являются характеристи­ками управляемого нелинейного элемента при значениях параметра у₀/а = 0,50,100,150 и 200. Обратим внимание на то, что y_lm/2a, px_w, у₀/а —вели­чины с нулевой размерностью. Если масштабы по оси уменьшить в ^2 раз, то кривые на рис. 15.15, б будут представлять собой характеристики по действующим значениям первых гармоник. Характеристика неуправляемого нелинейного элемента соответствует кривой, для которой y_Q / а = 0.

§ 15.24. Простейшая управляемая нелинейная индуктивность.

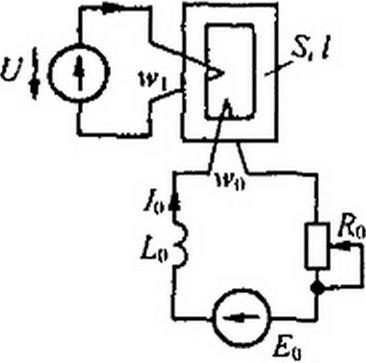
Простейшая управляемая нелинейная индуктивность изображена на рис. 15.17. Она образована обмотками и w₂, намотанными на замк­нутый ферромагнитный сердечник. Площадь поперечного сечения сер­дечника — 5 (м²), длина средней магнитной линии — I (м).

Обмотка включена в цепь переменного

тока, и по ней проходит переменный ток Z, со­держащий первую и высшие гармоники.

Обмотка управления (подмагничивания) w₀ присоединена к источнику постоянной ЭДС Е_о через дополнительную индуктивность £₀ и ре­гулируемое резистивное сопротивление Rq. По обмотке протекает постоянный ток Л) ⁼

Хотя переменный магнитный поток и наводит в обмотке переменную ЭДС, но переменный ток по ней практически не проходит, так как до­полнительная индуктивность £₀ образует для

переменного тока достаточно большое индуктивное сопротивление.

Пусть приложенное к обмотке Wj напряжение равно U_m cos со/. Это напряжение равно ЭДС самоиндукции, взятой с обратным знаком (актив­ное сопротивление обмотки считаем весьма малым):

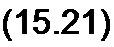Отсюда магнитный поток

Ф = sin о / + Ф_о - Ф_т sin со t + Ф_о;

СО H’j

Ф_т=и_т,(®ч). (15.22)

где Ф_т — амплитуда переменной составляющей магнитного потока; Ф_о — постоянная составляющая магнитного потока.

Управляемая нелинейность позволяет путем изменения постоянного тока /₀ в обмотке управлять переменным током i.

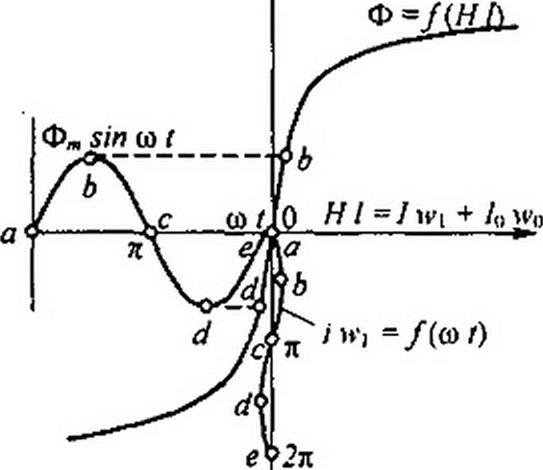
Принцип управления режимом ее работы и характер изменения во вре­мени отдельных величин поясним с помощью рис. 15.18, а, б, где кривые Ф = f(H I) представляют собой зависимости потока Ф в сер­дечнике от произведения напряженности магнитного поля Н на длину средней магнитной линии Z сердечника.

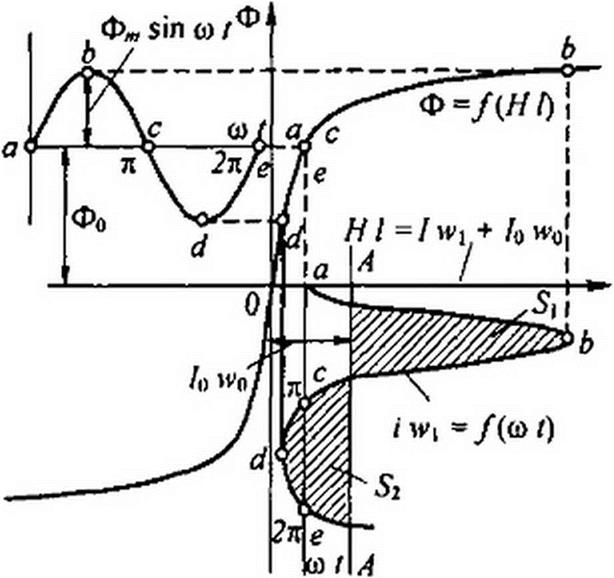
Построения на рис. ] 5.18, а соответствуют случаю, когда /₀ - 0, а на рис. 15.18, б — когда /₀ *0. На обоих рисунках переменная составляю­щая потока Ф_п} sin at одинакова. Для рис. 15.18, а постоянная состав­ляющая потока Ф_о = 0, для рис. 15.18, б Ф_о *0. На кривых Ф = /(со/),

Ф = /(Я/) И / W] ~ /(со /) наиболее характерные соответствующие друг другу точки обозначены одинаковыми буквами.

Построения производим в такой последовательности.

Сначала откладываем значения постоянной составляющей потока Ф_о и строим кривую Ф,_)} sin со /. Затем произвольно задаемся различными моментами времени, например равными со / = 0; я / 2; я; 3 / 2 я; 2 л, и для каждого значения со/ с помощью кривой Ф- f(H Г) находим соответ­ствующие значения НI и строим кривую i и>, + /₀ w₀ = /(со /) (для рис. 15.18, а /₀ w_Q —0), Ось времени для этой кривой направлена верти­кально вниз и проходит через точки а, с, е в нижней части рисунка.

Ток / не содержит постоянной составляющей, так как в цепи обмотки W] нет источника постоянной ЭДС и выпрямителей.

Прямая А—А (рис. 15.18, б) является нулевой линией для кривой / = /(со /). Ток i изменяется относительно этой прямой так, что сред­

нее значение его за период от со / = 0 до со / = 2 я равно нулю.

Другими словами, проводим прямую А—А так, чтобы площадь S, была равна площади 5₂. Расстояние, на которое удалена прямая А—А от оси ординат, равно /₀ w₀.

Полезно сопоставить выводы § 15.17, сделанные в обшей форме, с теми выводами,

которые применительно к нелинейному индуктивному элементу следуют из рассмотрения рис. 15.18, а, б. Сопоставимыми величинами являются х-Ф; y-(i+ /₀ м-₀); х₀-Ф₀; х_т-Ф_т v_q-/_om-₀; y = +/₀

а) в § 15.17 утверждалось, что путем изменения y_(t можно влиять на амплитуды пер­вой и высшей гармоник функции у- f(a)f) этот вывод подтверждается построениями на рис. 15.18, а, о — амплитуды первой и высших гармоник функции / и-, = /(со О зависят
от f₀ w₀ (чем больше /₀ w₀, тем больше амплитуда первой гармоники тока /);

б) уо зависит не только от Ф_о но и от Ф_ж, из построений рис. 15.18, а, б следует, что /₀ w₀ зависит не только от Ф_о, но и от Ф_т;

в) при наличии постоянной составляющей в составе функции х в кривой у = /(со/) появляются четные гармоники. Из рис. 15.18, б следует, что при наличии постоянной со­ставляющей в составе магнитного потока Ф в кривой = /(со/) появляются четные гармоники — кривая / wj = /(&>/) несимметрична относительно прямой А—А.

Запишем потоки через индукции и сечения:

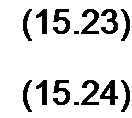Ф - В S-

Ф₀ == Bq S_y

где В_т — амплитуда переменной составляющей индукции; B_Q — по­стоянная составляющая индукции.

Из (15.22) и (15.23) следует, что

(15.25)

Если магнитную индукцию В_т выражать в Гс; 5 — см², U_m заме­нить на U V2, где U — действующее значение напряжения на обмотке то

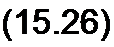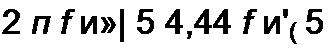Формула (15.25) дает возможность найти амплитуду переменной со­ставляющей магнитной индукции по амплитуде синусоидального напря­жения U_ту частоте / числу витков w, и сечению 5. По закону полного тока произведение напряженности поля Н на длину средней магнитной линии / должно быть равно алгебраической сумме МДС:

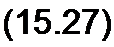Н I = i W] + l_Q Wq

Так как ток I содержит первую и высшие гармоники, то уравнение (15.27) распадается на ряд уравнений: уравнение для постоянных состав­ляющих, уравнения для первой гармоники, второй гармоники и т. д.

Уравнение для постоянных составляющих

(15.28)

где Hq — постоянная составляющая напряженности поля.

Переменный ток i содержит первую, вторую и другие высшие гармо­ники, но постоянной составляющей не содержит, так как в цепи обмот­ки и*| нет источника постоянной ЭДС и выпрямителей.

Уравнение для первой гармоники

(15.29)

где /_1лг — амплитуда первой гармоники тока г, Н_]п1 — амплитуда пер­вой гармоники напряженности поля.

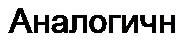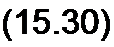Из (15.28)-(15.29) следует, что

//„ = /(> и-о//; (15.31)

Я_1ЛГ =/|_Л, W)//; (15.32)

(15.33)

и т. д.

Формула (15.31) позволяет определить постоянную составляющую напряженности поля H_Q через постоянную составляющую тока ^.Фор­мула (15.32) позволяет найти Н_Хт через 1_]т и т. д.

§ 15.25. ВАХ управляемой нелинейной индуктивности по первым гармоникам. Под ВАХ управляемой нелинейной индуктивности по пер­вым гармоникам будем понимать зависимость действующего значения первой гармоники переменного напряжения на обмотке w, от дей­ствующего значения первой гармоники переменного тока !_} при посто­янном токе /₀, взятом в качестве параметра.

Как уже указывалось в § 15.21, ВАХ нелинейной индуктивности мож­но получить опытным путем с помощью схемы (рис. 15.15, а) или рас­четным.

Рассмотрим расчетный путь, основанный на использовании обобщенных характерис­тик (см. § 15.23).

Пусть зависимость между мгновенным значением напряженности магнитного поля И и мгновенным значением магнитной индукции В выражается гиперболическим синусом:

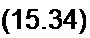/7=ashP В.

В (15.34) Н выполняет ту же функцию, что / в (15.1), а В — ту же. что и х.

На основании аналогии между (15.34) и (15.1) ясно, что характеристики управляемой нелинейной индуктивной катушки по первым гармоникам полностью совладают с харак­теристиками на рис. 15.16, б. если заменить на $В_1П, У\_т/2а — на Н_1т/2а, параметр у₀1а — на 7/₀/а.

Из (15.25) следует, что

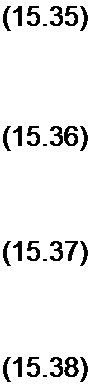е) iv, S о

р VT

Кроме того, из (15.32) имеем

Следовательно,

! -.Лв. ЛЛ.

¹ 2 a W|

На основании (15.31)

, Н_о al

l₀ =------------- •

a iv₀

Таким образом, для перехода от семейства кривых в безразмерных единицах 3 = /(Л/_1т/2а) при параметре 7/₀/а к семейству кривых С7, — /(/J при пара­

метре /₀ нужно масштаб по оси ординат изменить в он', S/ 41 раз, масштаб по оси абсцисс — в a // w₀ раз.

Пример 151. Управляемая нелинейная индуктивность (см. рис. 15.17) имеет следую­щие данные: 5 = 2,2 см²; / = 25см; uj=250; >v₀ = 1775. Аналитическое выражение кри­вой намагничивания Н = 0,71 sh5,75 В. Воспользовавшись кривыми =/(^|_m/(2 а)) при параметре у₀/а (см. рис. 15.16, 6). построить семейство ВАХ по первым гармони­кам Ц = /(/,) при параметре /₀.

Решение. Подсчитаем коэффициент для перехода от 0х_да к напряжению U:

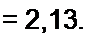думу S 314-250-2,210'⁴

Р 41 5,75 41

Таким образом, при переходе от р х_п, к напряжению U масштаб по оси ординат на рис. 15.16, б должен быть увеличен в 2.13 раза. Определим коэффициент для перехода от Н_]т /(2 а) к действующему значению первой гармоники тока:

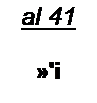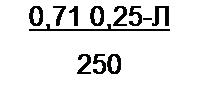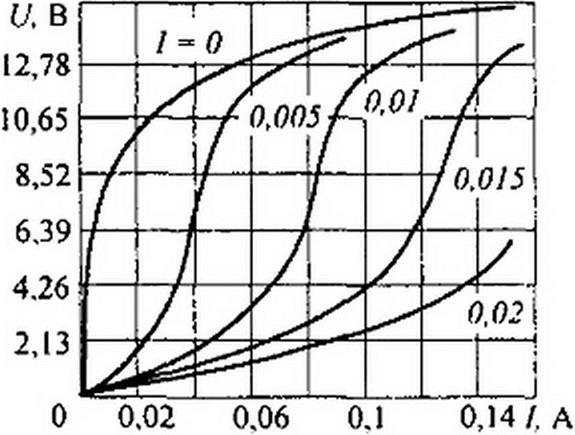
Следовательно, масштаб по оси абсцисс должен быть изменен в Ю“³ раз. Коэффици­ент для перехода от Hq /а к току /о

а/ 0.71 0.25

ИЪ ” 1775

Семейство ВАХ изображено на рис. 15.19.

В литературе, посвященной электричес­ким цепям с нелинейными индуктивными элементами, используют термин «индуктив­ное сопротивление» нелинейной индуктив­ности по первой гармонике.

Под индуктивным сопротивлением по первой гармонике понимают отношение дей­ствующего значения первой гармоники напряжения Ц на зажимах индуктивной катушки, включенной в цепь переменного тока, к действующему значению первой гар­моники тока /], протекающего через нее: Л'|=6'|//|, где ,V] —функция напряжения U_{ и тока подмагничивания /₀. Изменение

Л', в функции при /₀ = const и Д'] в функции /₀ при 4/| = const можно проанализи­ровать, воспользовавшись кривыми на рис. 15.19. Если L/₍=8.52B, то при /₀ = 0 /_t = 0,01 А, следовательно, = 8,52/0.01 = 852 Ом.

При /₀= 0.01 А =8,52/0.084 = 101 Ом. При /₀= 0,015 А ^=66,5 Ом.

Таким образом, изменяя ток подмагничивания /₀. можно управлять сопротивле­нием ,¥|.

Пример 152. Обмотка и', управляемой индуктивной катушки примера 152 подключе­на к источнику синусоидального напряжения С/, = 12,2 В (/ = 50 Гц). Обмотка управле­ния w_u подключена к источнику постоянной ЭДС £₀ = 1 В. Резистивное сопротивление цепи подмагничивания /?₀ = 50Ом. Определить амплитуду переменной составляющей и постоянную составляющую магнитной индукции.

Ре ш е н и е. По формуле (15.25),

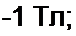
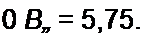12,2 VI

2 те-50< 250-2,2ПО^-4

Постоянные составляющие тока /₀ = Е_о / R_Q = 1/50 = 0,02 А и напряженности поля /7₀/а = /₀ м>₀//= 141,5 А/м.

Параметр Н_о /а = 141,5/0.71 = 200. По формуле (15.17),

0 В_о = Arsh------- —------- = 1,86; В_о ^2- = 0,324 Тл.

(7 5,75) р

§ 15.26. ВАХ управляемого нелинейного конденсатора по первым гармоникам. Кулон-вольтную характеристику нелинейного конденсатора приближенно можно описать гиперболическим синусом:

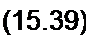и = a sh Р q.

q = Qo + Qn, sin (0 /,

где Qo — постоянная составляющая заряда; — амплитуда первой гармоники заряда.

При этом напряжение на конденсаторе имеет постоянную составляющую (/₀, а так­же первую и высшие гармоники. Формулы (15.12)-(15.15) можно распространить на не­линейный конденсатор, если заменить у₀ на (/₀; у_1л, на Ц„,; х„, на Q_m\ x_Q на Со В соответствии с этим постоянная составляющая напряжения на конденсаторе

4/₀ = a sh р & 7₀ (./0 &,). (15.40)

Первая гармоника напряжения

2 a ch р Со (-7 ⁷! (7 Р C_w)) sin со t.

Ток через конденсатор равен dq/dt. Следовательно, первая гармоника тока через него

— (С_м sin о /) = <о См cos и I. dt

Ее амплитуда со Q_m = 0 (?„, /0. а действующее значение в 77 Р^аз меньше:

(15.41)

Под ВАХ управляемого нелинейного конденсатора по первым гармоникам будем по­нимать зависимость действующего значения первой гармоники тока через конденсатор 1_} от действующего значения первой гармоники напряжения U\ при параметре U_o.

На основании записанного соответствия между U_Q и у₀ и U_[m и у_)п, и т. д. можно утверждать, что семейство кривых Р Q_m = /(2 а)) при параметре U_o /а. полностью

повторяет семейство кривых P*_w = /(}'i_M/(2a)) при параметре у$1а, изображенное на рис. 15.16, б.

Для перехода от семейства кривых Р Q_m = /(L'_tw /2 а) к семейству ВАХ управляемо­го нелинейного конденсатора по первым гармоникам следует учесть формулу (15.41) и то, что действующее значение первой гармоники напряжения на конденсаторе

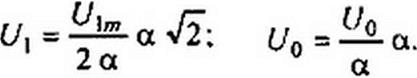Следовательно, для перехода от семейства кривых P(?_m = fW\m /(2 а)) при парамет­ре U₀/a к семейству кривых Ц = при параметре (/₀ необходимо масштаб по оси ординат изменить в ы/(р 77) раз, по оси абсцисс — в а 41 раз, параметр — в а раз. Подобно тому как для нелинейной индуктивной катушки вводят понятие индуктивного сопротивления по первой гармонике (см. § 15.25). для нелинейного конденсатора вводят

понятие емкостного сопротивления по первой гармонике: где U\ —действу­

ющее значение первой гармоники напряжения на конденсаторе; /₍— действующее зна­чение первой гармоники тока через нелинейный конденсатор; Xi — функция Ц и

Рассмотрим элементы теории транзисторов и применение последних в электрических цепях. В настоящее время применяют транзисторы двух типов: биполярные и полевые. Физические основы работы их различны. Сначала обсудим вопросы, относящиеся к биполярным транзисторам, а затем (см. § 15.35-15.37) — к полевым.

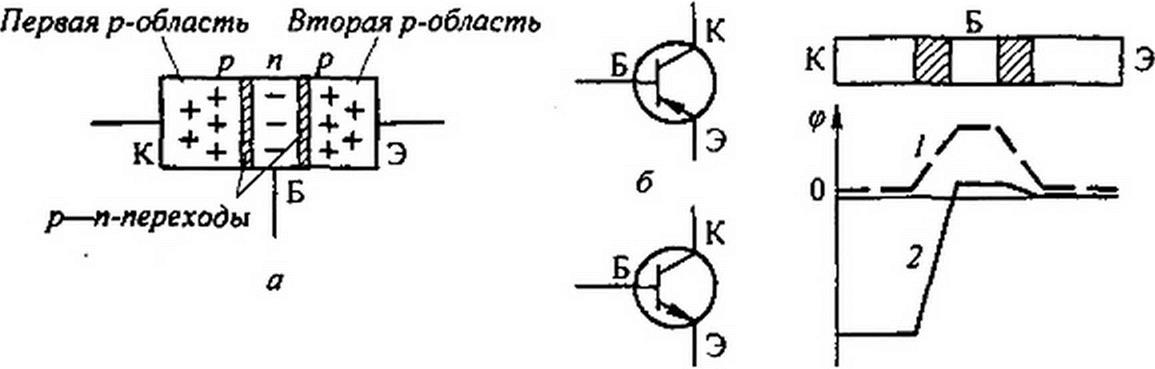
§ 15.27 Основные сведения об устройстве биполярного транзис­тора. Биполярным его называют потому, что его работа обусловлена но­сителями обеих полярностей. Транзистор представляет собой трехслой­ную структуру р—п—р- или и—р—«-типа. Схематически структура р—п—p-типа пояснена на рис. 15.20, а, где знаком плюс в р-области обо-

в г

Рис. 15.20

значены носители положительных зарядов, знаком минус в «-области — носители отрицательных зарядов. Оба переходных слоя между р- и «-областями обладают односторонней проводимостью. Ток через каждый из этих слоев может проходить практически в том случае, когда потен­циал р»-области выше потенциала «-области.

У транзистора имеется три вывода. В транзисторе р—«—p-типа пер­вый вывод — от первой ^-области — называют коллектором, второй вывод — от второй р-области — эмиттером, третий вывод — от «-об­ласти — базой.

На электрических схемах транзистор р—п—p-типа изображают, как показано на рис. 15.20, б, а транзисторы «—р—«-типа — в соответствии с рис. 15.20, в.

§ 15.28 Основные способы включения биполярных транзисторов в схему. Различают три основных способа включения триодов в схему в зависимости от того, какой из электродов транзистора является общим для управляющей и управляемой цепей.

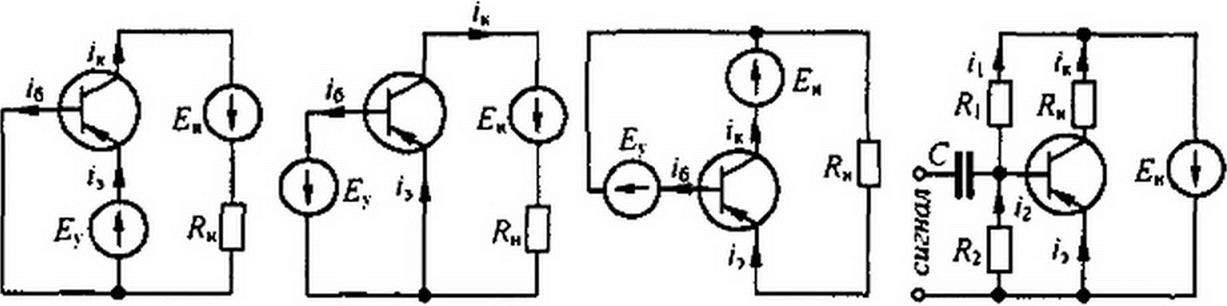
На рис. 15.21, а изображена схема с общей базой, на рис. 15.21, б — схема с общим эмиттером, на рис. 15.21, в — схема с общим коллек­тором.

Во всех схемах Е_н — источник ЭДС в цепи нагрузки; Е_у — источ­ник ЭДС в цепи управления. Для всех схем, в которых используют тран­зисторы р—полярность источников ЭДС должна быть такой,

а б в г

Рис. 15.21

чтобы коллектор имел отрицательный, а эмиттер положительный потен­циал относительно базы.

Для создания смещения на базе транзистора (напряжение ^Лбо) вме­сто отдельной ЭДС Е_у (рис. 15.21,6) используют делитель напряже­ния — резисторы R_} й /?₂, подключенные к £_н (рис. 15.21, г). В этом случае £Або⁼Ло^2» ^Лбо ⁺ Ло ⁼ Ло ⁺ Ло“Ло> ^г^^е Ло» Ло» /_б0 — постоянные составляющие токов /₂, Л- Сигнал на базу по­ступает через конденсатор С.

§ 15.29 Принцип работы биполярного транзистора. Если в крис­талл чистого германия или кремния (элементов четвертой группы таб­лицы Менделеева) внести ничтожное количество элементов пятой (мы­шьяк или сурьма) или третьей (бор или индий) группы, то в результате реакции замещения электрические свойства германия (кремния) резко изменятся. В месте внесения в германий (кремний) элементов пятой груп­пы (их называют донорами) образуются свободные электроны, а изме­ненный таким образом германий называют полупроводником «-типа. В месте внесения в германий элементов третьей группы (их называют рецепторами) будет недоставать электронов или, что то же самое, обра­зуется избыток дырок, выполняющих роль положительных зарядов. По­лучившийся при этом полупроводник называют полупроводником р-типа.

Под р—«-переходом понимают переход полупроводника p-типа в по­лупроводник «-типа. У транзистора р—«—p-типа два р—«-перехода (рис. 15.20, а). Через р—«-переход из «- в p-область диффундируют элек­троны, а из р- в «-область — дырки, образуя на границах перехода при­граничные избыточные заряды (на рис. 15.20, а они обозначены значка­ми + и -). Эти заряды создают на переходе потенциальный барьер, напряженность электрического поля которого Е_о направлена от пригра­ничных избыточных плюс-зарядов к приграничным избыточным минус - зарядам. Если в схеме рис. 15.21, а ЭДС Е_у и Е_к не включены, то потенциальный барьер правого перехода будет препятствовать переме­щению дырок от эмиттера к базе, а потенциальный барьер левого — перемещению электронов от базы к коллектору. Распределение потен­циала вдоль транзистора в этом случае иллюстрирует кривая 1 на рис. 15.20, г. Если же ЭДС в схеме рис. 15.21, а включены, то ЭДС будет создавать на правом р—«-переходе напряженность поля Е_у, направ­ленную против напряженности поля потенциального барьера £₀. При этом потенциальный барьер снизится и энергетический уровень части дырок окажется достаточным для того, чтобы они начали двигаться от эмиттера в тонкий слой базы. Там они частично рекомбинируют с элек­тронами базы и затем под действием ЭДС £_н через левый р—«-переход направляются к коллектору и эмиттеру (коллектор имеет отрицательный потенциал по отношению к эмиттеру и базе). Одновременно из базы дви­гаются электроны в направлении коллектора и эмиттера. Ток эмиттера равен сумме токов коллектора и базы ц=/_к+/_б. Отношение i_K / /_э = 0,95 * 0,99 зависит от типа транзистора и режима его работы. Рас­пределение потенциала Ф вдоль транзистора в рабочем режиме иллюс­трирует кривая 2 на рис. 15.20, г.