Характеристики, для которых выполняется условие у{-х) - у(х), на­зывают симметричными; характеристики, не удовлетворяющие этому условию, — несимметричными.

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Симметричными характеристиками обладают нелинейные индуктив­ности и емкости, а из резистивных — тиритовые сопротивления, элект­рическая дуга с однородными электродами и некоторые другие.

Однако основные типы нелинейных резистивных элементов — элек­тронная лампа, транзистор и тиристор — имеют несимметричные харак­теристики. Особенности работы нелинейных элементов с несимметрич­ными характеристиками — электронной лампы и транзистора — излага­ются в § 15.27-15.43.

§ 15.12 Аппроксимация характеристик нелинейных элементов. Для проведения математического анализа нелинейных цепей переменного тока и изучения их общих свойств целесообразно выразить аналитиче­ски зависимость между мгновенными значениями и и i для нелинейного резистора, зависимость между В и Н для нелинейной индуктивности, зависимость q и и для нелинейного конденсатора. Приближенное анали­тическое описание характеристик нелинейных элементов называют ап­проксимацией характеристик.

§ 15.13 Аппроксимация симметричных характеристик для мгно­венных значений гиперболическим синусом. При исследовании

свойств электрических цепей явлением гистерезиса, как правило, мож­но пренебречь. Лишь при исследовании цепей, в основе действия кото­

рых лежит это явление (например, работы запоминающих магнитных устройств с прямо­угольной петлей гистерезиса), гистерезис необ­ходимо учитывать.

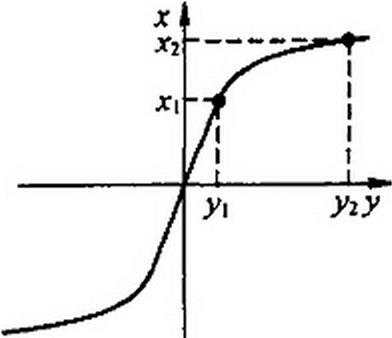
На рис. 15.11 изображена типичная симмет­ричная характеристика у - f(x).

Для нелинейной индуктивности роль х иг­рает мгновенное значение индукции В; роль у— мгновенное значение напряженности поля Н. Для нелинейного конденсатора у — это на­

пряжение w, х — заряд q. Для нелинейных Рис. 15.11

резисторов (например, тиритовых сопротивле­ний) роль х играет напряжение, у — ток.

Существует большое число различных аналитических выражений, в

той или иной мере пригодных для аналитического описания характерис­тик нелинейных элементов [24, 30]. При выборе наиболее подходящего аналитического выражения для функции у- /(х) исходят не только из

того, что кривая, описываемая аналитическим выражением, должна дос­таточно близко всеми своими точками расположиться к опытным путем полученной кривой в предполагаемом диапазоне перемещений рабочей точки на ней, но учитывают и те возможности, которые выбранное ана­литическое выражение дает при анализе свойств электрических цепей. В дальнейшем для аналитического описания симметричных характерис­тик по типу рис. 15.11 будем пользоваться гиперболическим синусом:

y = ashpx. (15.1)

В этом выражении аир — числовые коэффициенты; а выражает­ся в тех единицах, что и у; р — в единицах, обратных единицам х, так что произведение р х есть величина безразмерная. Для определения неизвестных коэффициентов а и Р следует на полученной опытным путем зависимости у - /(х) в предполагаемом рабочем диапазоне про­извольно выбрать две наиболее характерные точки, через которые долж­на пройти аналитическая кривая, подставить координаты этих точек в уравнение (15.1) и затем решить систему из двух уравнений с двумя неизвестными.

Пусть координаты этих точек y_f, х₍, и у₂, х₂ (см. рис. 15.11). Тогда

yi - a sh Р х,; у, = а sh Р х₂.

Отношение

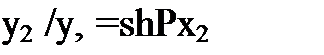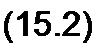Трансцендентное уравнение (15.2) служит для определения коэффи­циента р.

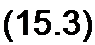Следовательно,

а = у₂ /sh р х₂ •

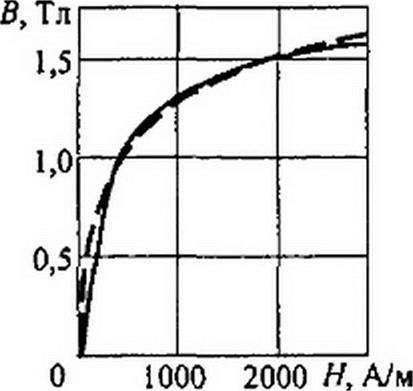
Пример 147. Кривая намагничивания трансформаторной стали Э41 изображена на

рис. 15.12. Найти коэффициенты а и 0.

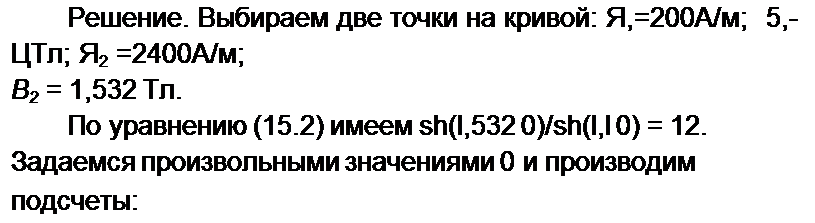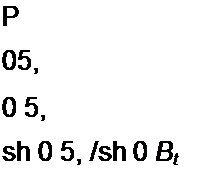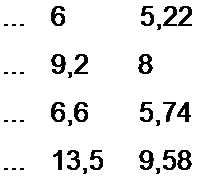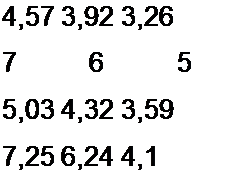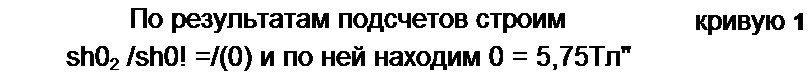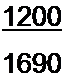Штриховая линия на рис. 15.12 построена по уравнению Н ~ 0,71 sh(5,75 В).

Таблица 15.1

§ 15.14 Понятие о функциях Бесселя. При анализе нелинейных цепей широко ис­пользуют функции Бесселя, которые являются решением уравнения Бесселя

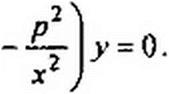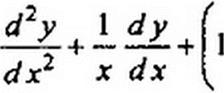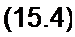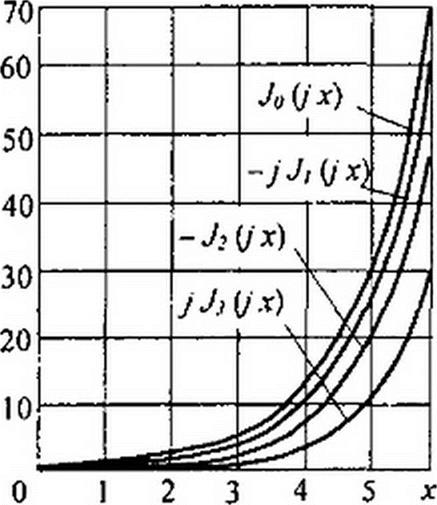
Функции Бесселя выражают степенными рядами, и для них составлены таблицы. Фун­кцию Бесселя от аргумента х обозначают J_p(x\ где р — порядок функции Бесселя. Общее выражение для J_р{х) в виде степенного ряда можно записать так:

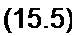(х/2)^р _ (х/2)'”² (х/2)^р+А _ (х/2)^р*⁶ ₊

0\р1 1!(р + 1)! ⁺2!(р + 2)! 3!(р+3)! ⁺

Для гл. 15 наибольший интерес представляют фун­кции Бесселя от чисто мнимого аргумента (табл. 15.1). Для их получения в общее выражение (15.5) вместо х следует подставить j х, где J - 4~Л. Обратим внима- ние на то, что в табл. 15.1 даны функция -j J\(j х) вместо J[(j х) и функция j J₃(J х) вместо Jy(jх). Сделано это потому, что без дополнительного мно­жителя/или -/ эти функции, как правило, не исполь­зуют.

При х= 0 не равна нулю только функция Бесселя нулевого порядка: J_o(0) = l. По данным табл. 15.1 на рис. 15.13 построены кривые функции Бесселя. Отку­да видно, что с ростом х значения функций увеличи­ваются. Чем выше порядок функции Бесселя, тем мень­ше ее значение при одном и том же х.

§ 15.15 Разложение гиперболических синуса и

косинуса от периодического аргумента в ряд Фурье. Если аргумент х изменяется по периодическому закону, например по закону синуса x = x_wsinco/, где х„ —амплитуда колебаний, то по периодическому закону изменяются и функции sh(x_m sin со г) и ch(x_m sin со/).

Так как периодические функции можно представить рядами Фурье, то разложим в ряд Фурье эти функции. С этой целью в (15.5) вместо х подставим х_т sin со/. Учтем извест­ные из тригонометрии формулы

sin² а = 0,5-0,5 cos 2 а; (15.6)

sin³ а = -0,25 sin 3 а + 0,75 sin а; (15.7)

sin⁴ а = 0,375-0.5 cos2 а + 0,125 со$4 а, (15.8)

сгруппируем все слагаемые с sin со/, cos2co/, sin3co/ и т. д., а также отдельно выделим постоянную составляющую. В результате оказывается, что коэффициентами при тригоно­метрических функциях являются ряды, которыми изображают функции Бесселя различ­ных порядков от чисто мнимого аргумента j х_т.

Окончательно получим

sh(x_m sin со /) = 2 (-/ J) (/ х„,)) sin со / - 2 J J₃(j x_m) sin 3 со / - 2 / J₅ (/ х_да) sin 5 со / -...;

(15.9)

ch(x_m sin со/) = J о (j x_m) + 2 j J₂(j x„,) cos 2 co / + 2 j(j x„,)cos4 co / + .... (15.10)

Ряд для sh(x_OT sin co/) состоит только из нечетных гармоник и не имеет постоянной составляющей. Ряд для ch(x_m sin со/) имеет постоянную составляющую и четные гармо­ники.

Пример 148. Разложить в ряд Фурье sh(4 sin со t) и ch(4sin<o0* Решение. Значения функций Бесселя берем из табл. 15.1:

-J Л (J 4) = 9,76; j J₃ (j 4) = 3,34; J₄ (j 4) = 1,416;

-J Ji (j 4) = 0,505; J_o (y 4) = 11,3; J₂ (y 4) = -6,42.

В соответствии с (15.9) и (15.10) получим

sh(4 sin со t) = 2 ■ 9,76 sin to t - 2 ■ 3,34 sin 3 co / + 2 • 0,505 sin 5 w r -...;
ch(4 since t) = 11,3-2-6,42 cos 2 or + 2-1,416 cos 4 co/ + ....

§ 15.16 Разложение гиперболического синуса от постоянной и синусоидально меняющейся составляющих в ряд Фурье. Из § 15.13 известно, что мгновенное значе­ние функции у связано с мгновенным значением х формулой (15.1). 8 этой формуле аргу­ментом гиперболического синуса является не х, как было в § 15.14, а произведение 0х. В соответствии с этим для разложения sh(P х_т sin coz) и ch(P х„ sin со /) в (15.9) и (15.10) следует заменить х на Р х_т.

Если х = х₀ + х_т sin а/, где х₀ —постоянная составляющая, х„ —амплитуда сину­соидальной составляющей, то

у = a sh(P х₀ + р x_ni sin «/) = а sh Р х₀ ch(P х_т sin со /) + а ch р х₀ sh(P х„, sin со /).

Следовательно,

У - a sh р х₀(( J_Q {j р х_т)) + 2 J₂ (j р х_т) cos 2 со t + 2 J₄ (j р х„,) cos 4 со / +...) + +2 а ch р х₀ ((-у J| (у Р х_т)) sin со / - у J₃ U р х„) sin 3 о t -...). (15.11)

Из (15.11) следует, что постоянная составляющая функции у

v₀ =ashpx₀ У₀(УРх_да). (15.12)

Первая гармоника функции у

У> = 2achpx₀ (-у У, (у Px_w))sino/; (15.13)

вторая гармоника

у, = 2 a sh Р х₀ J₂ (j Р х„) cos 2 со /; (15.14)

третья гармоника

Уз - 2achpx₀ (-у J₃ (j р х„,)) sin 3 си t. (15.15)

и т. д.

Пример 149. Разложить в ряд Фурье функцию у/а = sh(2 + 4 sin о/).

Решение. По табл. 8.1 находим sh2 = 3.63; ch2 = 3,7. Значения функций Бесселя берем из табл. 15.1. В соответствии с (15.11)

у/a = sh(2 + 4 sin о z) - 3,63 (11,3-12.844 cos 2 со г + 2,832 cos4 со/-...) +
+3,76 (19.52 sinw t - 6,674 sin 3 co t +1,01 sin5 co / -...).

Таким образом, y₀ /a = 41,1; у_1ж /a = 73,4; y_2m /a = 46,7.