Нелинейные электрические цепи переменного тока

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§ 15.1. Подразделение нелинейных элементов. Нелинейными элек­трическими цепями переменного тока называют электрические цепи переменного тока, в состав которых входит один или несколько нелиней­ных элементов.

Как известно, прохождению переменного тока оказывают сопротив­ление не только резистивные, но и индуктивные и емкостные элементы. В соответствии с этим нелинейные элементы для переменного тока мож­но подразделить на три группы:

1) резистивные;

2) индуктивные;

3) емкостные.

Каждую из этих групп можно подразделить на управляемые и неуп­равляемые.

Управляемые нелинейные элементы обычно имеют один или несколь­ко управляющих электродов (зажимов) или управляющих обмоток, вклю­чаемых в управляющую цепь (цепи), воздействуя на ток или напряжение которых можно управлять сопротивлением в главной цепи. При отсут­ствии специальных управляющих электродов или обмоток управляющий ток или напряжение могут воздействовать на нелинейный элемент через электроды или обмотки главной цепи.

§ 15.2 Общая характеристика нелинейных резисторов. Широкое распространение в качестве управляемых нелинейных резистивных эле­ментов получили трех- (и более) электродные лампы, транзисторы и ти­ристоры. Свойства, принцип работы, характеристики и применение их рассмотрены в § 15.27-15.43.

Неуправляемыми нелинейными резистивными элементами в упомя­нутом смысле являются электрическая дуга, германиевые и кремниевые диоды, тиритовые сопротивления, терморезисторы, бареттеры, лампы накаливания и др. Их основные свойства и ВАХ рассматривались в гл. 13.

Нелинейные резистивные элементы можно классифицировать также по степени влияния температуры нагрева, обусловленной протекающи­ми по ним токами, на форму ВАХ.

Так как тепловые процессы (процессы нагрева и остывания) являют­ся процессами инерционными, то резисторы, нелинейность ВАХ кото­рых в основном обусловлена изменением температурь! в результате на­грева протекающим через них током, принято называть инерционными.

Резисторы, нелинейность ВАХ которых обусловлена иными (не теп­ловыми) процессами, принято называть безынерционными или почти безынерционными.

К группе инерционных резисторов относят электрические лампы на­каливания, терморезисторы, бареттеры; к группе безынерционных или почти безынерционных — электронные лампы, полупроводниковые ди­оды, транзисторы и др.

Если постоянная времени нагрева инерционного резистора много больше периода пе­ременного тока, то значение сопротивления его за период переменного тока практически не меняется, так как оно определяется не мгновенным, а действующим значением пере­менного тока. Если к такому резистору подвести синусоидальное напряжение (при усло­вии, что постоянная времени нагрева его значительно больше периода синусоидального напряжения), то ток через него будет практически синусоидальным.

Можно сказать, что такие резисторы занимают промежуточное положение между ли­нейными и нелинейными. К нелинейным они тяготеют вследствие того, что сопротивле­ние их является функцией действующего значения тока; к линейным — потому, что в установившемся режиме работы их сопротивления для различных моментов времени внут­ри периода воздействующей на схему ЭДС остаются практически неизменными.

§ 15.3 Общая характеристика нелинейных индуктивных элемен­тов. Под нелинейными индуктивными элементами понимают индуктив­ные катушки (индуктивности) с обмотками, намотанными на замкнутые сердечники из ферромагнитного материала, для которых зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейна. Индуктивное сопротивление таких катушек, оказываемое про­хождению переменного тока, не постоянно; оно зависит от значения пе­ременного тока. Условимся называть их нелинейными индуктивными катушками или нелинейными индуктивностями.

Нелинейные индуктивности подразделяют на управляемые и неуправ­ляемые, но деление на безынерционные и инерционные на них не рас­пространяется, так как их нелинейность обусловлена свойствами ферро­магнитного материала, а не тепловым эффектом.

На электрических схемах нелинейную индуктивную катушку изобра­жают в виде замкнутого сердечника с обмоткой (рис. 15.1, а) или как показано на рис. 15.1, б.

Сердечники нелинейных индуктивных катушек р-н при относительно низких частотах делают обычно

двух типов: пакетные и спиральные.

"» Пакетные сердечники состоят из тонких пластин

ферромагнитного материала кольцевой, П- или ^а б Ш-образной формы.

Рис. 15.) Спиральные сердечники изготовляют из тонкой

ферромагнитной ленты. По форме они напоминают туго навитую часовую пружину.

Пластины пакетного и отдельные витки спирального сердечников изолируют друг от друга эмалевым лаком, жидким стеклом или ка­ким-либо иным изолирующим составом и запекают. Изоляция необходи­ма для уменьшения потерь энергии в сердечнике от вихревых токов (см. § 15.4).

При высоких частотах резко возрастают потери в листовых сердеч­никах, поэтому сердечники, предназначенные для работы на высоких частотах, выполняют обычно из магнитомягкого феррита.

§ 15.4 Потери в сердечниках нелинейных индуктивных катушек, обусловленные вихревыми токами. Если по индуктивной катушке со

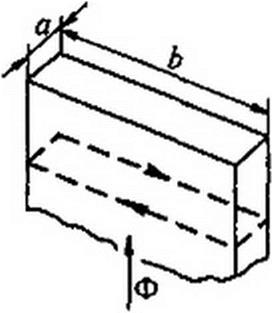
стальным сердечником проходит переменный ток, то в сердечнике воз­никает переменный магнитный поток, под действием которого в листах сердечника образуются вихревые токи. На рис. 15.2 изображен один лист сердечника. Пусть магнитный поток, увеличиваясь, направлен вверх (вдоль листа). В плоскости листа, перпендикулярной

магнитному потоку, по закону электромагнитной ин­дукции наводится ЭДС. Эта ЭДС вызывает в нем ток, который называют вихревым. Контур, по которому замыкается вихревой ток, изображен штриховой лини­ей на рис. 15.2. Вихревые токи, по закону Ленца, стре­мятся создать поток, встречный по отношению к вы­звавшему их потоку.

Потери энергии в листе на вихревые токи пропор­циональны квадрату наведенной в контурах листа ЭДС и обратно пропорциональны сопротивлению контуров.

ЭДС, наводимые в контурах, по которым замыкаются вихревые токи, при заданной ширине листа Ь пропорциональны толщине листа а, амплитуд­

ному значению индукции и частоте. В свою очередь, сопротивление кон­тура пропорционально его периметру и удельному сопротивлению. При b»а периметр контура почти не зависит от толщины листа. Поэтому потери энергии на вихревые токи пропорциональны квадрату

амплитудного значения индукции, квадрату частоты и квадрату толщи­ны листа.

Уменьшить потери в листовом сердечнике на вихревые токи можно двумя путями:

1 ) изготовлением сердечника из тонких изолированных друг от друга листов (см. § 15.3);

2 ) добавлением в ферромагнитный материал примесей, увеличива­ющих его удельное сопротивление.

При частоте 50 Гц толщина листов обычно 0,35-0,5 мм; при высоких частотах — до 0,005 мм.

Кроме потерь от вихревых токов в сердечнике есть еще потери, обус­ловленные гистерезисом и магнитной вязкостью.

3 15.5. Потери в ферромагнитном сердечнике, обусловленные ги­

стерезисом. Как известно (см. § 14.4), ферромагнитным материалам свой­

ственно явление гистерезиса, которое вызвано отставанием изменения магнитной индукции от изменения напряженности магнитного поля. Площадь гистерезисной петли в координатах В, Н (В — индукция, Н — напряженность поля), снятая при достаточно медленном изменении маг­нитного поля во времени (когда вихревые токи практически отсутству­ют), характеризует энергию, выделяющуюся в единице объема ферромаг­нитного материала за один период переменного тока (за одно перемаг­ничивание). Потери в сердечнике, обусловленные гистерезисом, пропор­
циональны объему сердечника, первой степени частоты и площади гис­терезисной петли. От толщины листов потери на гистерезис не зависят'*.

Гистерезисные петли при достаточно быстром изменении магнитно­го поля во времени называют динамическими. Динамические петли шире соответствующих статических за счет вихревых токов и магнитной вяз­кости.

Степень отличия динамической петли от соответствующей статиче­ской зависит от скорости перемагничивания (от частоты), удельного элек­трического сопротивления материала, толщины листов, температуры и наличия в магнитном потоке высших гармоник.

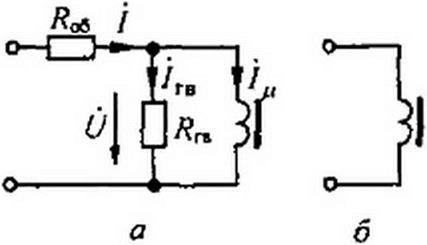
4 15.6. Схема замещения нелинейной индуктивности. В расчетном отношении нелинейную индуктивную катушку (рис. 15.1, а} можно представить в виде схемы на рис. 15.3, а. В ней параллельно с идеали­зированной (без потерь) нелинейной индуктивностью включено сопро­тивление 7?_гв, потери в котором имитируют потери энергии в сердечни­ке на гистерезис и вихревые токи, а последовательно включено резис­тивное сопротивление самой обмотки /?_об; U— напряжение на нелиней­ной индуктивности.

Как уже отмечалось, потери энергии на гистерезис и вихревые токи /?_гв зависят от качества ферромагнитного материала и толщины листов сердечника.

Если сердечник выполнен из низкокачественного магнитного матери­ала, то потери в нем относительно велики, а сопротивление R_rB доста­точно мало и ток /_Г8 = U / R_rB может оказаться соизмеримым с током /_р, протекающим по идеализированной (без потерь) нелинейной индуктив­ности; в этом случае ветвь с сопротивлением Я_гв необходимо учитывать в расчете.

Если же сердечник изготовлен из тонких листов высококачественно­го магнитомягкого материала, то потери в сердечнике малы, а сопротив­ление /?_гв =U² / Р_гв очень велико, и потому ветвь с сопротивлением Я_гв можно не учитывать.

Часто вводят еще одно упрощение: полагают резистивное сопротив­ление обмотки /?_об настолько малым, что с падением напряжения в нем можно не считаться. Аналогичное упрощение часто делалось и при рас-

5* Явление поверхностного эффекта (см.: Бессонов Л.А. Теоретические основы элект­ротехники. Электромагнитное поле: Учебник. М.: Гардарики. 2001) здесь не учитываем.
чете цепей с линейными индуктивностями, В этом случае сопротивле­ние катушки со стальным сердечником оказывается чисто индуктивным (соответствующая схема замещения представлена на рис. 15.3, б).

Переход от схемы замещения на рис. 15.3, а к схеме замещения на рис. 15.3, б вызван стремлением облегчить расчет цепей. При этом учи­тывают основной полезный нелинейный эффект (нелинейность между индукцией В и напряженностью Н, приводящая к усилению магнитного потока за счет свойств ферромагнитного материала) и пренебрегают по­бочным вредным эффектом (потерями, обусловленными гистерезисом и вихревыми токами в сердечнике).

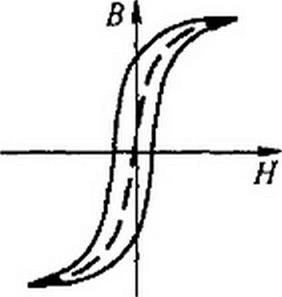
При периодическом процессе нелинейность между В и Н учитывают, ведя расчет по кривой, абсциссы которой равны полусумме абсцисс восходящей и нисходящей ветвей предельной гистерезисной петли (рис. 15.4).

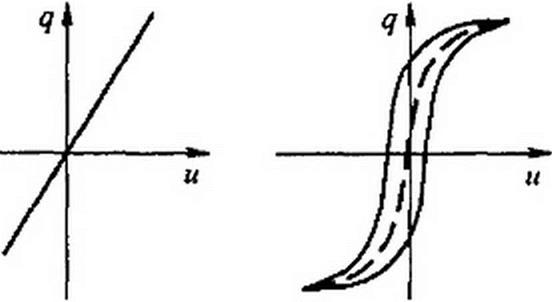
§ 15.7 Общая характеристика нелинейных емкостных элементов. В обычных конденсаторах обкладки разделены веществом, диэлектриче­ская проницаемость которого не является функцией напряженности элек­трического поля. Для них зависимость мгновенного значения заряда q на одной обкладке от мгновенного значения напряжения и между обклад­ками (кулон-вольтная характеристика) представляет собой прямую линию (рис. 15.5), а их емкость не зависит от напряжения и. Для нелинейных конденсаторов зависимость q от и нелинейна (рис. 15.6).

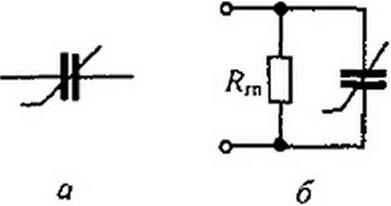
Нелинейные конденсаторы называют еше варикондами. На электри­ческих схемах вариконды изображают в соответствии с рис. 15.7, а. Про­странство между обкладками вариконда заполняют сегнетодиэлектриком. Сегнетодиэлектриками называют вещества, диэлектрическая проница­емость которых является функцией напряженности электрического поля. Название «сегнетодиэлектрики» им присвоено потому, что впервые это свойство было обнаружено у кристаллов сегнетовой соли.

Сегнетодиэлектрики, подобно ферромагнитным веществам, обладают гистерезисом. Электрическим гистерезисом называют явление отстава­ния изменения электрического смещения D от изменения напряженнос­ти поля Е. Как и в ферромагнитных веществах, площадь гистерезисной петли в координатах D, Е при медленном изменении поля характеризует потери на электрический гистерезис в единице объема сегнетодиэлект- рика за один период изменения Е.

Кроме потерь на гистерезис в варикондах есть еще потери, обуслов­ленные тем, что проводимость сегнетодиэлектрика не равна нулю, а также вязкостью процессов поляризации.

На схеме замещения вариконд можно представить в виде параллель­ного соединения идеализированного (без потерь) вариконда и ветви с резистивным сопротивлением Я_гп, потери в котором имитируют в рас­четном отношении активные потери в вариконде (рис. 15.7, б).

Наличие потерь в варикондах является вредным побочным э

Чем выше качество сегнетодиэлектрика, тем уже петля гистереза и мень­ше потери в нем. Для облегчения исследования свойств электрических цепей, содержащих вариконды, гистерезисом и потерями обычно пре­небрегают и зависимость q- f(u) принимают в виде штриховой линии на рис. 15.6. Абсциссы ее равны полусумме абсцисс восходящей и нис­ходящей ветвей предельной гистерезисной петли. Однако при исследо­вании схем, в основе действия которых лежит явление гистерезиса, например при анализе работы некоторых запоминающих и счетных устройств, гистерезис необходимо учитывать.

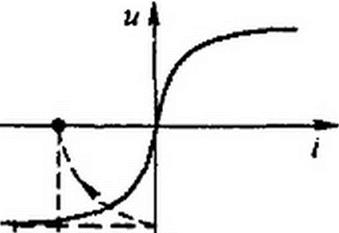
§ 15.8 Нелинейные элементы как генераторы высших гармоник тока и напряжения. Если нелинейный элемент, например резистор, при­соединить к генератору синусоидального напряжения, то проходящий через него ток будет иметь несинусоидальную форму и потому нелиней­ный резистор будет являться генератором высших гармоник тока. Для того чтобы убедиться в этом, рассмотрим рис. 15.8, где кривая / — ВАХ HP; кривая 2 — синусоидальное напряжение на нем; кривая 3 — ток через HP.

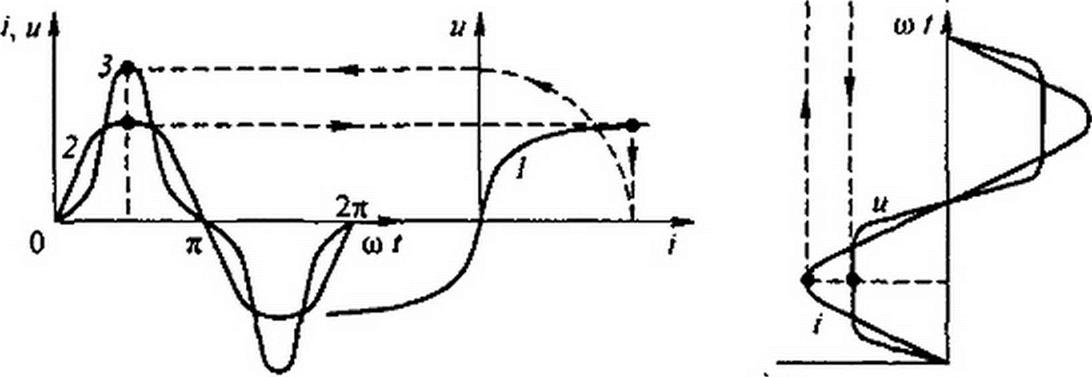
Для построения кривой i = /(cor) последовательно придает со Г зна­чения, равные, например, 0, л/6, п/ 4, л/З, л/2 и т. д.; для каждого из них находим напряжение и, переносим соответствующее значение и на кривую и =f(i) и из нее определяем значение тока i для взятого момента
времени. Найденное значение тока i откладываем на той ординате, кото­рой соответствует выбранный момент времени.

Эти операции показаны на рис. 15.8 стрелками. Так, по точкам стро­им кривую 3. Она имеет пикообразную форму и может быть разложена на гармоники.

Аналогично, если через нелинейный резистор пропустить синусои­дальный ток, то напряжение на нем будет иметь несинусоидальную фор­му. Соответствующие построения приведены на рис. 15.9. Следователь­но, нелинейный резистор является генератором высших гармоник напря­жения.

Амплитуды первой и высших гармоник токов нелинейно зависят от амплитуд первой и высших гармоник напряжений на нелинейных элемен­тах. Это затрудняет анализ и расчет нелинейных цепей и в то же время позволяет осуществить с их помощью ряд важных в практическом отно­шении преобразований, принципиально невыполнимых с помощью ли­нейных электрических цепей при неизменных во времени параметрах.

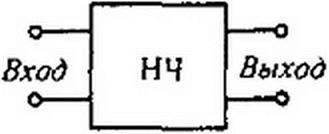
§ 15.9 Основные преобразования, осуществляемые с помощью нелинейных электрических цепей. На рис. 15.10, а схематически изоб­ражен четырехполюсник, в состав которого входят одно или несколько нелинейных элементов. Будем называть такой четырехполюсник нелиней­ным (НЧ).

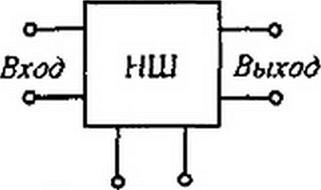
На рис. 15.10, б представлен нелинейный шестиполюсник (НШ). В отличие от четырехполюсника он имеет еще два зажима («полюса»), к которым присоединяется источник управляющего напряжения или тока.

С помощью нелинейных четырех- и шести пол юс ни ков можно осуще­ствить ряд практически важных преобразований:

1) преобразовать переменный ток в постоянный. Устройства, предна­значенные для этого, называют выпрямителями (см. § 15.54);

2) преобразовать постоянный ток в переменный с помощью устройств, которые называют автогенераторами (см. § 15.55) и инверторами;

3) осуществить умножение частоты, т. е. получить на выходе четырех­полюсника напряжение, частота которого в несколько раз больше часто­ты входного напряжения. Четырехполюсники, с помощью которых про­изводят умножение частоты, называют умножителями частоты; устрой­ство, удваивающее частоту, —удвоителем частоты; устройство, утраи­вающее частоту, —утроителем и т. д.;

4) произвести деление частоты, т. е. выполнить операцию, обратную умножению частоты. Четырехполюсники, используемые для этого, назы­вают делителями частоты',

5) стабилизировать напряжение (ток), т. е. получить на выходе четы­рехполюсника напряжение (ток), почти не изменяющееся по модулю при значительном изменении входного напряжения. Такие четырехполюсни­ки называют стабилизаторами напряжения (тока). Устройства для ста­билизации напряжения в цепях постоянного тока рассмотрены в гл. 13;

6) осуществить триггерный эффект, т. е. эффект резкого (скачкообраз­ного) изменения выходной величины при незначительном изменении входной. Триггерный эффект рассмотрен в § 15.58 и 15.60;

7) произвести модуляцию. Как указывалось в § 7.15, модуляция есть процесс, при котором амплитуда (фаза или частота) высокочастотного колебания, поступающего на вход четырехполюсника, преобразуется та­ким образом, что характер изменения ее повторяет характер изменения управляющего низкочастотного сигнала. Устройства, предназначенные для этого, называют модуляторами;

8) осуществить демодуляцию, т. е. выделить из высокочастотного модулированного колебания запечатленный в нем низкочастотный управ­ляющий сигнал. Устройства для демодуляции называют демодуляторами или детекторами;

9) преобразовать желаемым образом форму входного напряжения. Например, при подаче на вход нелинейного четырехполюсника напряже­ния синусоидальной формы на его выходе можно получить напряжение прямоугольной или пикообразной формы;

10) произвести усиление напряжения (тока), т. е. получить на выходе нелинейного устройства напряжение значительно большее, чем управля­ющее напряжение на его входе. Управляющее напряжение может быть постоянным или переменным. С помощью трансформаторов также можно усиливать напряжение, однако в усилителях напряжения на нелинейных элементах энергия, потребляемая управляющей цепью, может быть в сотни, тысячи и даже сотни тысяч раз меньше энергии на выходе усили­теля, тогда как в обычных трансформаторах эти энергии почти равны. Усилители напряжения на нелинейных элементах позволяют усиливать не только переменное, но и постоянное напряжение и притом с плавным изменением коэффициента усиления;

11) осуществить усиление мощности, т. е. выделить на выходе устрой­ства (в нагрузке) мощность, значительно большую мощности, поступа­ющей в управляющую цепь. Когда говорят об усилении мощности, то имеют в виду, что приращение мощности, выделяющейся в нагрузке, оказывается больше приращения мощности, потребовавшейся для изме­нения режима работы нелинейного элемента;

12) произвести степенное и логарифмическое преобразования вход­ного напряжения (тока).

С помощью нелинейных электрических цепей кроме перечисленных можно осуществить и другие нелинейные преобразования. К их числу относится, например, плавное преобразование частоты с помощью не­линейных четырех- и шестиполюсников, не содержащих подвижных ча­стей. Рассмотрение этого преобразования выходит за рамки курса (см. [21]).

Нелинейные устройства широко применяют для умножения электри­ческим путем двух, трех функций и более, а также в электрических счет­ных и запоминающих устройствах, в качестве нелинейных фильтров, логических устройств и т.п. Несомненно, что по мере развития техники и изучения свойств нелинейных цепей последние будут находить приме­нение для выполнения и других функций.

Если зависимость выходной величины от входной в относительно небольшом диапазоне может быть линейной или близкой к линейной, то в большинстве случаев стремятся выбрать режим работы преобразова­теля таким образом, чтобы работа его проходила именно на линейном участке (если это не противоречит назначению преобразователя).

13) 15.10. Некоторые физические явления, наблюдаемые в нелиней­ных цепях. В электрических цепях переменного тока, содержащих не­линейные индуктивности и линейные или нелинейные конденсаторы и линейные индуктивности, а также нелинейные индуктивности и нелиней­ные конденсаторы, при определенных условиях (далеко не всегда!) воз­никают физические явления, которые невозможны в линейных цепях^Ф). Таких явлений довольно много. Ограничимся кратким рассмотрением только некоторых, наиболее важных из них.

1. Возникновение интенсивных колебаний в цепи на высшей гармони­ке при отсутствии этой гармоники во входном напряжении. В линейных цепях возникновение интенсивных колебаний на высшей гармонике мо­жет быть только при наличии этой гармоники во входном напряжении.

2. Возникновение субгармонических колебаний. Под субгармоникой понимают гармонику, частота которой в целое число раз меньше часто­ты источника ЭДС. Субгармонические колебания представляют собой колебания на какой-либо из суб гармоник. Чаще всего они наблюдаются на частотах со/3; со/2; <х>/5 и т. д. (со —частота источника ЭДС) (см. § 15.69).

3. Возникновение колебаний в цепи на гармонике с частотой т<&1 п, где т и п — целые числа.

4. Зависимость характера установившегося режима в нелинейной цепи переменного тока от предшествовавшего этому режиму состояния цепи и начальной фазы источника ЭДС. Это явление может наблюдаться в нелинейных электрических цепях в зоне существования триггерного эф­фекта, о котором было упомянуто в § 15.9. Суть явления состоит в том, что при подключении нелинейной резонансной цепи к источнику ЭДС в ней может возникнуть один из двух возможных режимов. Какой из ре­жимов возникнет, зависит от начальной фазы генератора и состояния цепи, предшествовавшего включению (см. § 15.58).

‘'Имеются в виду обычные линейные цепи, параметры которых не являются функци­ей времени. О линейных цепях с непостоянными во времени параметрами см. гл. 18.

5. Возникновение авто модуляции. Автомодуляция представляет собой процесс почти периодического изменения амплитуд токов и напряжений в нелинейных электрических цепях без воздействия на них внешнего модулирующего фактора, т. е. без воздействия на них низкочастотного сигнала (см. § 15.70).

6. Хаотические колебания, перемежающиеся резонансы и другие типы движений.

Перечисленные физические явления имеют место в резонансных це­пях только в определенных для каждой цепи диапазонах параметров, которые, как правило, оказываются такими, что практически эти явления наблюдаются сравнительно редко. Кроме того, исследование условий возникновения этих явлений часто связано с громоздкими математиче­скими выкладками. В настоящей книге они рассмотрены в § 15.58, 15.60, 15.69, 15.70 и в Приложении П9. Подробно можно ознакомиться с этими явлениями также по [24, 25].

§ 15.11 Разделение нелинейных элементов по степени симметрии характеристик относительно осей координат. Кроме деления на рези­стивные, индуктивные и емкостные, управляемые и неуправляемые (а резистивных — еще на безынерционные и инерционные) нелинейные элементы можно классифицировать еще по одному признаку — по сте­пени симметрии характеристик для мгновенных значений относительно осей координат.

Пусть х и у — величины, характеризующие режим работы нелиней­ного элемента. Условимся х обозначать величину, откладываемую по оси ординат декартовой системы, ъ у — величину, откладываемую по оси абсцисс.