Тангенс угла наклона прямой возврата к оси абсцисс называют коэф­фициентом возврата. Его числовые значения для различных магнито­твердых материалов даются в руководствах по постоянным магнитам.

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Обозначим длину оставшегося воздушного зазора (см. рис. 14.18, 6) =5-/_мг и на основании закона полного тока запишем 1 Mv

Н_с /_с + //₅₁ 5, +/_мс Я_мс=0.

Напряженность поля в магнитомягком материале Н_мс много меньше напряженности поля в магнитотвердом материале и в воздушном зазоре при одном и том же значении магнитной индукции, поэтому слагаемым Я_мс ^мс пренебрегаем по сравнению с остальными. При этом

Н = -0,8’10⁶ (14.21)

Магнитное состояние постоянного магнита определяется пересечени­ем прямой возврата с прямой, построенной по (14.21).

Пример 145. Воздушный зазор магнита из примера 155 уменьшен вдвое. Найти ин­дукцию в нем.

Решение. Находим р = 131,5 10². Прямая ОА (см. рис. 14.18, в) пересекается с пря­мой возврата в точке d. Поэтому В_с = 0,42Тл. Такая же индукция будет и в воздушном зазоре, так как = S_c.

Следовательно, уменьшение зазора со значения 6 до 8| привело к увеличению маг­нитной индукции в нем с 0,3 до 0,42 Тл.

Если же зазор 8₍ получить не путем его уменьшения со значения 8 до 8_t, а путем выемки из намагниченного сердечника куска длиной 8_И то магнитное состояние магни­та определится пересечением луча АО с кривой размагничивания baf в точке е.

В этом случае В_с = В₆ = 0,48 Тл, т. е. возрастет на

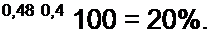
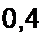Таким образом, магнитный поток в постоянном магните зависит не только от размера воздушного зазора, но и от предыстории установления этого зазора.

§ 14.23 Магнитное сопротивление и магнитная проводимость участка магнитной цепи. Закон Ома для магнитной цепи. По опре­делению, падение магнитного напряжения (7_М = И 1_У но

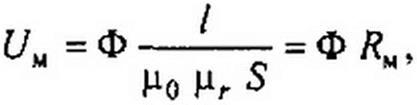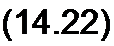где S — площадь поперечного сечения участка. Следовательно,

откуда

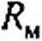(14.23)

Уравнение (14.22) называют законом Ома для магнитной цепи. Это уравнение устанавливает связь между падением магнитного напряже­ния U_u и потоком Ф; R_M называют магнитным сопротивлением участ­ка магнитной цепи. Величину, обратную магнитному сопротивлению, называют магнитной проводимостью-.

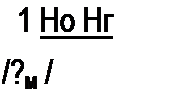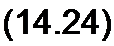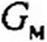Из предыдущего известно, что вебер-амперная характеристика учас­тка магнитной цепи в общем случае нелинейна. Следовательно, в общем случае и G_M являются функциями магнитного потока (непостоянны­ми величинами). Поэтому практически понятиями /?_м и G_M при расче­тах пользуются в тех случаях, когда магнитная цепь в целом или ее уча­сток, для которых определяются /?_м и G_M, не насыщены. Чаще всего это бывает, когда в магнитной цепи имеется достаточно большой воздушный зазор, спрямляющий вебер-амперную характеристику магнитной цепи в целом или ее участка.

Магнитное сопротивление участка цепи R_u можно сопоставить со статическим сопротивлением нелинейного резистора R_CJ (см. § 13.10) и так же, как последнее, R_M можно использовать при качественном рас­смотрении различных вопросов, например вопроса об изменении пото­ков двух параллельных ветвей при изменении потока в неразветвленной части магнитной цепи (как в § 13.2 относительно электрической цепи).

Пример 146. Найти /?_м воздушного зазора постоянного магнита и магнитный поток, если 6 = 0,5 см, площадь поперечного сечения воздушного зазора 5 = 1,5 см², (/_м = 1920 А.

Решение:

r = L — ----------------------- LL12----------- _т = 0,256-10* Гн’¹;

Mo Mr 5 1,257-Ю’⁶-1-1,5-IO’⁴

_{ф =} £м_ ₌ —¹⁹Л° ₌ 72зо. ] О’⁸ Вб,

Л_м 0,256-10®

где 1 — в мм; S — в м².

В заключение отметим, что если воспользоваться понятием магнит­ного сопротивления, то второй закон Кирхгофа (см. формулу (14.10)) для любого контура магнитной цепи, содержащей п участков, может быть записан так:

Л л

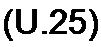51^ “ 52Л ^w k‘

к=\ к*1

Практически формулой (14.25) как расчетной удается воспользовать­ся, когда магнитная цепь не насыщена и R_Mk не является функцией Ф_к. Если же имеет место насыщение, то Я_ык является функцией Ф_к (т. е. неизвестны R_Mk и Ф_к) и при использовании формулы (14.25) воз­никают известные трудности.

§ 14.24 Магнитная линия с распределенными параметрами. На рис. 14.19, а изображена магнитная линия, образованная двумя протяжен­ными ферромагнитными стержнями, расположенными в воздухе, дли-

ной /, радиусом я, расстояние между осями стержней d « /, короткие вертикальные участки линии имеют длину l_ah. На левом участке распо­ложена обмотка w, сопротивлением /?, по которой протекает постоянный ток I от источника постоянной ЭДС Е. На конце линии нагрузка Я_мн.

Е w

Магнитное напряжение в начале линии (7_м1 =----------------------------------------------------------- И l_af) [Л], в конце

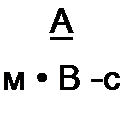линии <7_м2. Вдоль стержней проходит постоянныЛо времени магнитный
поток Ф_м[В-с]. Продольное магнитное сопротивление единицы длины

2

обозначим R_uo =—₂— лд р_а

а

рис. 14.19, б. Расстояние от начала линии до произвольной точки обозна­чим х, от конца линии —у, поток — Ф_м, магнитное напряжение — U*.

Используя аналогию с электрической линией с распределенными па­раметрами (см. гл. 11) запишем два уравнения:

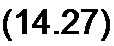V» = У«2 chv^ + Ф^ Лмв shvy, (14.26)

и = „ ^{sh v} У + ^ф2м chvy
^ямв

Здесь = 7Я_мо /С7_м0 — волновое магнитное сопротивление линии

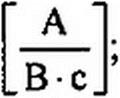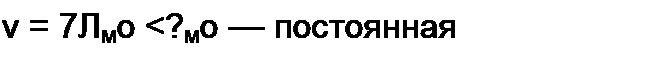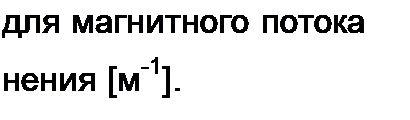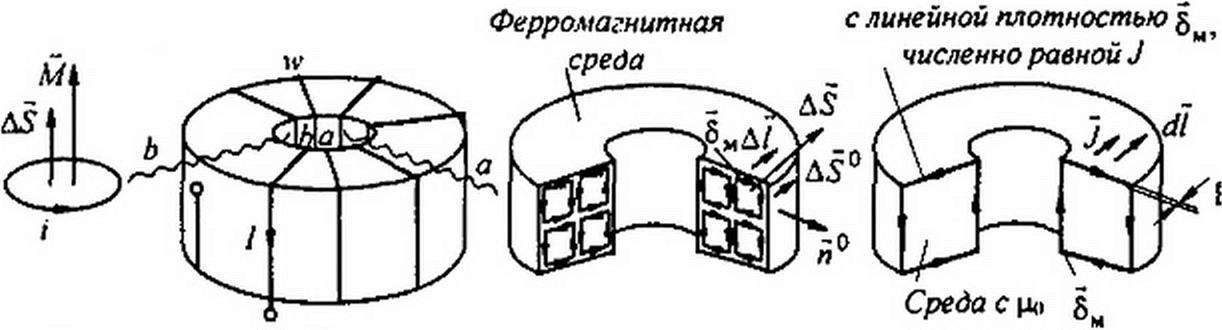
§ 14.25 Пояснения к формуле В = Контур с током /, охватывающий пло­

щадку Д5 создает магнитный момент M = iS <рис. 14.20, а). Вектор AS численно ра­вен площади AS. а положительное направление aS связано с положительным направ­лением тока i правилом правого винта.

Ферромагнитный кольцевой сердечник (рис. 14.20, б) имеет обмотку с числом витков и-, по которой проходит ток /. Каждая единица объема ферромагнитного материала обла­дает некоторым вектором намагниченности J, что при расчете можно рассматривать как результат наличия в ферромагнитном .материале контуров с молекулярными токами. Эти токи показаны в сечениях сердечника по линиям Ьа на рис. 14.20, в (намагничивающая обмотка с током не показана).

Среднюю линейную плотность молекулярного тока, приходящегося на единицу дли­ны сердечника в направлении Д/. обозначим (А / см). Единичный вектор, совпадаю­щий по направлению с направлением обозначим й°. Молекулярный ток д/й° охватывает площадку AS. Положительное направление вектора AS = ASSq связано с по­ложительным направлением этого тока правилом правого винта. Через S_o обозначен еди­ничный вектор по направлению as.

По определению, намагниченность J представляет собой магнитный момент едини­цы объема вещества. Среднюю по объему намагниченность вещества J можно найти делением магнитного момента контура с током 8 д/Я⁰, охватывающим площадку AS,

на объем А/ = Д/ AS:

^5м7-Ц⁶- S₀=6_M

Д/ AS ^{0 м}

Следовательно, средняя по объему намагниченность J численно равна средней линей­ной плотности молекулярного тока и направлена по $₀.

Как видно из рис. 14.20, в, на участках, являющихся смежными между соседними кон­турами, молекулярные токи направлены встречно и, если ферромагнитное тело намагни­чено равномерно, взаимно компенсируют друг друга. Нескомленсированными остаются только токи по периферийному контуру (рис. 14.20, г).

Наличие областей самопроизвольной намагниченности в ферромагнитном теле при расчете можно эквивалентировать протеканием по поверхности этого тела, считая его не­ферромагнитным, поверхностного тока с линейной плотностью причем по модулю 5_М = J,

Запишем уравнение по закону полного тока для контура, внутри равномерно намаг­ниченного сердечника рис. 14.20, б. При этом учтем, что после введения поверхностного тока сердечник станет неферромагнитным и будет намагничиваться не только током /, про­текающим по обмотке с числом витков w, но и поверхностным током с линейной плотно­стью б_м.

На длине dl поверхностный ток равен б_м dl -J dl. На длине всего сердечника он равен dJdl. Таким образом, q—dl - J w + qj dl. Отсюда q--------------------------------------------------------------------------------- J \dl = / iv.

J £ ^J ЧМо /

Величину----------- J обозначают H и называют напряженностью магнитного поля.

В отличие от магнитной индукции В и намагниченности J напряженность поля Н не зависит от магнитных свойств намагничиваемого тела (см. пример 139). Это и явилось основанием для того, чтобы закон полного тока для любых сред записывать в виде $Hd1 = / w.

Если ферромагнитное тело намагничено неравномерно по высоте и толщине, то плот­ность молекулярных токов смежных контуров на рис. 14.20, в неодинакова, а токи на смеж­ных между соседними контурами участках компенсируются не полностью. Отсюда следу­ет, что неравномерно намагниченное ферромагнитное тело при расчете можно заменить таким же в геометрическом смысле неферромагнитным телом, по поверхности которого течет поверхностный ток, плотность которого изменяется по высоте тела, а во внутрен­них точках тела течет объемный ток, плотность которого также изменяется от точки к точке.

Вопросы для самопроверки

1. Дайте определения В, j_t Н, Ф, ц_а, Но, р_г. Как они связаны между собой и 8 каких единицах выражаются? 2. В чем отличие начальной, основной и безгистерезисной кривых намагничивания? 3. Что понимают под частным и предельным циклами, прямой возврата, остаточной индукцией, коэрцитивной си,той, магнитомягкими и магнитотвердыми материалами? 4. Чем физически объясняются потери на гистерезис? Как их определить, располагая петлей гистерезиса? 5. Сформулируйте закон полного тока. 6. Дайте определе­ние следующим понятиям: МДС, магнитная цепь, магнитопровод, ветвь магнитной цепи. 7. Как определить направление МДС? 8. С какой целью стремятся выполнить магнитную цепь с возможно меньшим воздушным зазором? 9. Как выбирают направление магнитных потоков а ветвях? 10. Сформулируйте первый и второй законы Кирхгофа для магнитных цепей. 11, Поясните, как построить вебер-амперную характеристику участка цепи. 12. Пе­речислите этапы расчета цепей методом двух узлов. 13. В чем отличие магнитного напря­жения от падения магнитного напряжения? 14. Как экспериментально получить постоян­ный магнит? 15. Как рассчитывают магнитную цепь с постоянным магнитом? 16. Что понимают под магнитным сопротивлением /?_м участка цепи? магнитной проводимостью? От каких факторов они зависят? Зависят ли они от магнитного потока по участку цепи? Запишите второй закон Кирхгофа с использованием .понятия /?_м. 17. Сформулируйте за­кон Ома для участка магнитной цели. 18. Могут ли В и Н в ферромагнитном материале быть направлены встречно? 19. Решите задачи 3.2; 3.10; 3.13; 3.15; 3.19.

Глава пятнадцатая