Первый закон Кирхгофа: алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю'.

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

(14.9)

Первый закон Кирхгофа для магнитных цепей следует из принципа непрерывности магнитного потока, известного из курса физики (см. так­же том 2 учебника).

Второй закон Кирхгофа: алгебраическая сумма падений магнитного напряжения вдоль любого замкнутого контура равна алгебраической сумме МДС вдоль того же контура:

(14.10)

Второй закон Кирхгофа для магнитных цепей, по сути дела, есть иная форма записи закона полного тока.

Перед тем как записать уравнения по законам Кирх­гофа, следует произвольно выбрать положительные на­правления потоков в ветвях и положительные направле­ния обхода контуров.

Если направление маг­нитного потока на некото­ром участке совпадает с на­правлением обхода, то паде­ние магнитного напряжения этого участка входит в сум­му ^{с0 знак}<>м плюс, если встречно ему, то со знаком минус.

Аналогично, если МДС совпадает с направлением обхода, она входит в УI w со знаком плюс, в противном случае — со знаком минус.

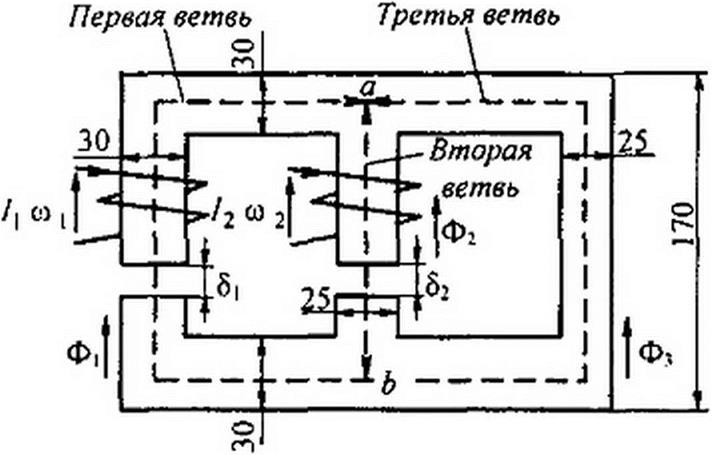
В качестве примера составим уравнения по законам Кирхгофа для раз­ветвленной магнитной цепи, изображенной на рис. 14.12.

Левую ветвь назовем первой, и все относящиеся к ней величины за­пишем с индексом / (поток Ф_и напряженность поля длина пути в стали /_и длина воздушного зазора 8), МДС 7_t О]).

Среднюю ветвь назовем второй, и все относящиеся к ней величины будут соответственно с индексом 2 (поток Ф₂, напряженность поля Н₂, длина пути в стали 1₂, длина воздушного зазора 8₂, МДС I₂ w₂).

Все величины, относящиеся к правой ветви, имеют индекс 3 (поток Ф₃, длина пути на вертикальном участке Z₃, суммарная длина пути на двух горизонтальных участках /₃).

Произвольно выберем направление потоков в ветвях. Положим, что все потоки (Ф|, Ф₂, Ф₃) направлены вверх (к узлу а). Число уравне­ний, которые следует составить по законам Кирхгофа, должно быть рав­но числу ветвей цепи (в рассматриваемом случае нужно составить три уравнения).

По первому закону Кирхгофа необходимо составить столько уравне­ний, сколько в цепи узлов без единицы (см. § 2.8).

В цепи (рис. 14.12) два узла; следовательно, по первому закону Кирх­гофа составим одно уравнение:

Ф₍ + Ф₂ + Ф₃ = 0. (4.11)

По второму закону Кирхгофа следует составить число уравнений, равное числу ветвей, за вычетом числа уравнений, составленных по пер­вому закону Кирхгофа. В рассматриваемом примере по второму закону Кирхгофа составим 3-1-2 уравнения.

Первое из этих уравнений составим для контура, образованного пер­вой и второй ветвями, второе — для контура, образованного первой и третьей ветвями (для периферийного контура).

Перед составлением уравнений по второму закону Кирхгофа необхо­димо выбрать положительное направление обхода контуров. Будем обхо­дить контуры по часовой стрелке.

Уравнение для контура, образованного первой и второй ветвями, имеет вид:

Н\ А ⁺ ^81 Sf " ^2 ^2 ~ ^Ь2 $2 ⁼ Л “ h ^W2' (4Л2)

где и И₈₂ — напряженности поля соответственно в воздушных за­зорах 8| и 8₂.

В левую часть уравнения вошли слагаемые Я, /, и H_5l 8j со знаком плюс, так как на первом участке поток Ф! направлен согласно с обходом контура, слагаемые Н₂ 1₂ и Я_$2 3₂ — со знаком минус, так как по­ток Ф₂ направлен встречно обходу контура.

В правую часть уравнения МДС l_x вошла со знаком плюс, так как она направлена согласно с обходом контура, а МДС /₂ и>₂ — со знаком минус, так как она направлена встречно обходу контура.

Составим уравнение для периферийного контура, образованного пер­вой и третьей ветвями:

Н_}1^Н_ЪХ 8,-Н'Л-Н\ w,. (4.13)

Совместно решать уравнения (4.11 )-(4.13) с тремя неизвестными (Ф], Ф₂> Ф₃) не будем, так как в § 14.8 дается решение рассматриваемой задачи более совершенным методом, чем метод на основе законов Кир­хгофа, — методом двух узлов.

§ 14.15 Применение к магнитным иепям всех методов, использу­емых для расчета электрических цепей с нелинейными резистора­ми. В гл. 13 подробно рассматривались различные методы расчета элек­трических цепей с HP. Эти методы полностью применимы и к расчету магнитных цепей, так как и магнитные и электрические цепи подчиня­ются одним и тем же законам — законам Кирхгофа.

Аналогом тока в электрической цепи является поток в магнитной цепи, аналогом ЭДС — МДС, аналогом вольт-амперной характеристики нели­нейного резистора — вебер-амперная характеристика участка магнитной цепи.

§ 14.16 Определение МДС неразветвленной магнитной цепи по заданному потоку. Заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного ма­териала и магнитный поток или индукция в каком-либо сечении. Требу­ется найти МДС, ток или число витков намагничивающей обмотки.

Расчет проводим в такой последовательности:

1) разбиваем магнитную цепь на участки постоянного сечения и оп­ределяем длины 1_к (м) и площади поперечного сечения S_k (м²) участ­ков (длины участков берем по средней силовой линии);

2) исходя из постоянства потока вдоль всей цепи, по заданному пото­ку и сечениям S_k находим магнитные индукции на каждом участке: В, =Ф/5,;

3) по кривой намагничивания определяем напряженности поля Н_к для ферромагнитных участков магнитной цепи; напряженность поля в воздушном зазоре

Н = 0,8-10⁶ В, (14.14)

где Н — в А / м; В — в Тл;

4) подсчитываем сумму падений магнитного напряжения вдоль всей магнитной цепи ^Н_к 1_к и на основании закона полного тока прирав­ниваем эту сумму к полному току / w: ^Н_к l_k = I w.

Основным допущением при расчете является то, что магнитный по­ток вдоль всей магнитной цепи полагаем неизменным. В действительно­сти небольшая часть потока всегда замыкается минуя основной путь. Например, для магнитной цепи (см. рис. 14.6) поток, выйдя из левого сердечника, в основном направляется по пути macbn, но небольшая часть потока идет по воздуху по пути mqn.

Поток, который замыкается минуя основной путь, называют потоком рассеяния. При малом воздушном зазоре поток рассеяния относительно мал; с увеличением воздушного зазора поток рассеяния может стать со­измеримым с основным потоком.

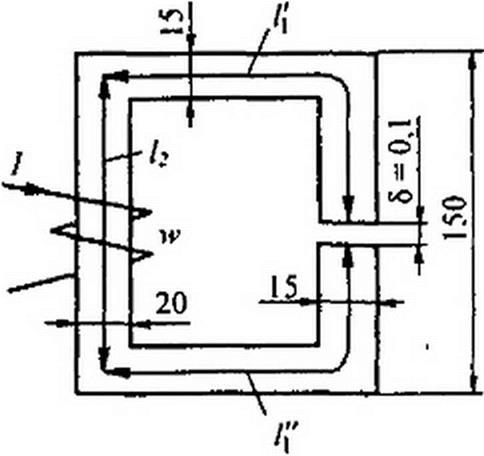
Пример 141, Геометрические размеры магнитной цепи даны на рис. 14.13 в милли­метрах; кривая намагничивания показана на рис. 14.9. Какой ток должен протекать по обмотке с числом витков w - 500, чтобы магнитная индукция В в воздушном зазоре 5 была В - 1 Тл?

Решение. Магнитную цепь разбиваем на три участка: Ц % /j +1* = 30 см;

5_t=4,5cM²; /₂= 13,5 см; 5,= 6 см². ,

Воздушный зазор 6 = 0,01 см; = 5| = 4.5 см². Индукция By - В_& = 1 Тл.

Индукция на участке /3 5₂ ^{= ф z} $2 = S5 /$2 = 1 • 4,5/ 6 = 0,75 Тл.

Напряженности поля на участках /₍ и /₂ определяем согласно кривой намагничива­ния (см. рис. 14.9) по известным значениям В) и В₂ : 7/. = 300 А/м; 7/₂=115А/м.

Напряженность поля в воздушном зазоре = 0.8-10 -В₅ = 0,8-Ю⁶ 1 = 810^s А/м.

Падение магнитного напряжения вдоль всей магнитной цепи:

£//* /*=//. /_t +Я₂/₂ + /7₆ 6 = 300 0.3 + 115 0.135 + 8-10⁵ 10⁴ = 185.6 А.

Ток в обмотке 7 “ 4 /н» = 185,6/500 = 0,371 А.

5) 14.17. Определение потока в неразветвленной магнитной цепи по заданной МДС. Заданы геометрические размеры магнитной цепи, кривая намагничивания и полный ток. Определить поток.

Для решения задачи необходимо построить зависимость потока в функции от 1_к и на ней найти рабочую точку.

Пример 142. Найти магнитную индукцию в воздушном зазоре магнитной цепи при­мера 141, если 7 и» = 350 А.

Решение. Задаемся значениями В = 0,5; 1.1; 1.2; 1,3Тл — и для каждого из них под­считаем 4 ^{так же}» ^{как в} предыдущей задаче. В результате получим:

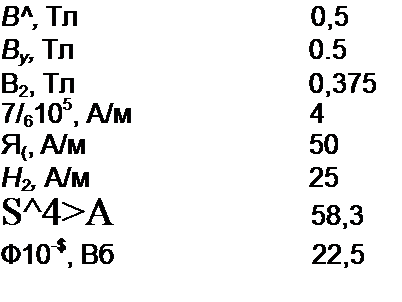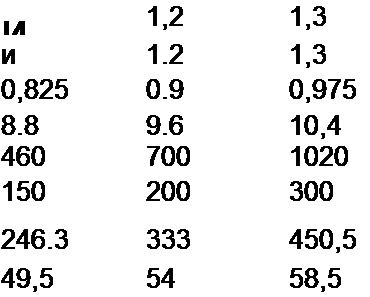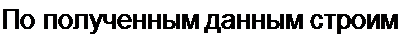зависимость Ф = /(£//* 4), изображенную на рис. 14.14, и по ней находим, что при 7w = 350A Ф = 5510^-$Вб Следовательно, _о Ф 55 10'⁵

В_ъ = — =--------------- _г = 1.21 Тл.

4,5 10“⁴

§ 5.18 , Расчет разветвленной магнитной цепи методом двух уз­лов. Ранее отмечалось, что для расчета разветвленных магнитных цепей применимы все методы, рассмотренные в гл. 13.

Рассчитаем разветвленную магнитную цепь (см. рис. 14.12) методом двух узлов.

Пример 143. Геометрические размеры магнитной цепи рис. 14.12 даны в миллимет­рах; кривая намагничивания представлена на рис. 14.9; /,^=80 A; /₂w₂ =300A;

= 0.05 мм; б₂ = 0.22 мм. Найти магнитные потоки в ветвях магнитной цепи.

Решение. Как и в схеме на рис. 13.6, узловые точки обозначим буквами а и Ь. Вы­берем положительные направления потоков Ф_ь Ф₂. Ф₃ к узлу а. Построим зависимость потока Ф₍ отпадения магнитного напряжения первой ветви Для этого произвольно задаемся рядом числовых значений Д,. Для каждого значения 5, по кривой намагничи­вания находим напряженность на пути в стали по первой ветви.

Падение магнитного напряжения на первом участке = Н_} + 0,8-10⁶ ■ 6,, где /₍ = 0,24 м — длина пути в стали по первой ветви. Выбранному значению соответ­ствует Ф, = В] S).

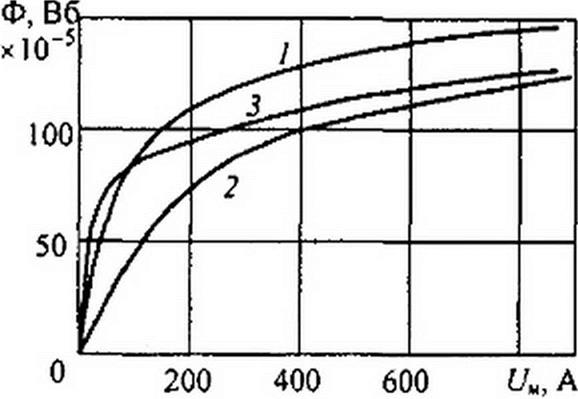
Таким образом, для каждого значения потока Ф] подсчитываем (7_М, и лоточкам стро­им зависимость Ф₍ = /(6/_М|) — кривая / на рис. 14.15.

Аналогично строим зависимость Ф₂ = f{U_u2) — кривая 2 на рис. 14.15; (/_м2 = н₂ А +0,8-10⁶ • В₂ б₂, где /₂ = 0,138 м — длина пути в стали во второй ветви.

Кривая 3 есть зависимость Ф₃ = /({/_м3). - Н'₃ Г₃ + Н₂ /₃, где /₃ * 0,1 и

/₃ « 0.14 м. Им соответствуют участки третьей ветви, имеющие сечения 9 и 7,5 см².

Магнитная цепь (см. рис. 14.12) формально аналогична нелинейной электрической цепи (см. рис. 13.6), Аналогами /_t и /₂ электрической цепи (см. рис. 13.6) являются магнитные потоки Ф, и Ф₂ магнитной цепи (см. рис. 14.12), аналогом ЭДС — МДС /, аналогом зависи­мости тока в первой ветви от падения напряжения на сопротивлении первой ветви (Z, = /(Ц)) — зависимость магнитного потока Ф₁ в пер­вой ветви магнитной цепи от падения магнитного напряжения £7_м] вдоль первой ветви (Ф₍ = /(Ц_м)) и т. д.

Воспользуемся аналогией с нелинейной электрической цепью для определения потоков Ф_н Ф₂, Ф₃. С этой целью выполним графические построения, подобные построениям на рис. 13.6.

Вспомним, что кривые (см. рис. 13.6) представляют собой зависимо­сти токов в ветвях схемы не от падений напряжений (Ц, L/₂, Uy) вдоль
этих ветвей, а от напряжения U_ab между узлами а и b схемы (см. рис. 13.6).

В соответствии с этим введем в расчет магнитное напряжение — раз­ность магнитных потенциалов — между узлами а и b: U^ab = Ф._Ма ~ФмЛ-

Выразим магнитный потенциал точки п(<р_ма) через магнитный потен­циал точки А>(ф_м/>), следуя от точки Ъ к точке а сначала по первой ветви, затем по второй и, наконец, по третьей. Для первой ветви

Фма =Ф_м*-(#1 А +Н_М 5,) + /,

где Н_} /| + //_Sl 5, = t/_M1 — падение магнитного напряжения по первой ветви. Знак минус перед скобкой обусловлен тем, что при перемещении согласно с направлением потока магнитный потенциал (как и электри­ческий при перемещении по току) снижается (если бы двигались против потока, то магнитный потенциал возрастал и нужно было бы ставить плюс). Плюс перед w_} свидетельствует о том, что при перемещении от точки b к точке а идем согласно с направлением МДС /₍ Таким образом, для первой ветви

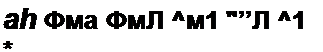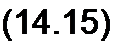для второй ветви (перемещаясь от b к а по потоку Ф₂ и согласно с на­правлением МДС /₂ w₂ )

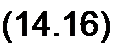
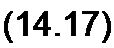^м2 ~ ”^м2 ⁺ Л ^w2>

для третьей ветви (на ней МДС отсутствует)

~ “^мЗ-

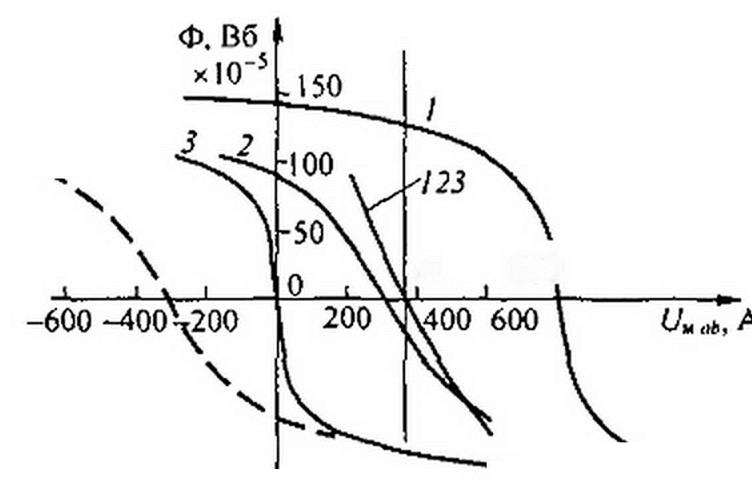
Графическое решение задачи приведено на рис. 14.16. На нем зависимость Ф) = представлена кривой /; Ф₂ ~ /(^_МЛ/>) —

кривой 2; Ф₃ - f{U_Mab) — кривой 3. Построение их производилось так же, как и построение соответствующих кривых на рис. 13.9. Начало кривой / смещено в точку 4/_мй/> ~ h ^wi =800 А; начало кривой 2 — в точку U_UUh - /₂ w₂ = 300 А. Кривая 123 представляет собой

Ф₁ + Ф₂ + Ф₃ = /(£/_м ab\ Она пересекает ось абсцисс в точке т. Прове­дем через точку т вертикаль и найдем потоки в ветвях:

Ф, =126,2И0’⁵ Вб; Ф₂ =-2510"⁵ Вб; Ф₃ =-101,2-10"⁵ Вб.

В результате расчета потоки Ф₂ и Ф₃ оказались отрицательными. Это означает, что в действительности они направлены противоположно по­ложительным для них направлениям, показанным стрелками на рис. 14.12.

Рассмотрим, какие изменения произошли бы в построениях на рис. 14.16, если бы какая-либо из МДС изменила направление на противоположное, например в результате изменения направления протекания тока в этой обмотке. Допустим, что изменилось на противоположное направление МДС /₂ н>₂. В уравнение (14.16) МДС /₂ и»₂ вошла бы теперь с отрицательным знаком. При построениях это нашло бы свое отражение в том, что кривая 2 переместилась влево параллельно самой себе так, что пересекла бы ось абс­цисс не в точке =300 А, а в точке U„_a(, = -300 А (штриховая линия 2'). Кривые / и 3 останутся без изменений, но суммарная кривая + Ф₂ +Ф₃ = f(U*_ab} будет иная.

§ 14.1 <>, Дополнительные замечания к расчету магнитных цепей. 1. При построе­нии ВАХ участков магнитной цепи в § 14.12 и далее явление гистерезиса не учитывалось. Поэтому ВАХ выходили из начала координат, не зависели от предыдущих процессов на­магничивания и размагничивания и удовлетворяли соотношению ф(-6/_м) = --Ф((7_М). Если учитывать гистерезис, то у ВАХ каждой ветви будут неодинаковые восходящий и нисхо­дящий участки, которые, в свою очередь, зависят от магнитного состояния, предшеству­ющего рассматриваемому (от магнитной предыстории). В этом случае Ф(-£/_м) * -Ф(£7_М). Для получения более правильных результатов при построении ВАХ следует учитывать гистерезис, что практически возможно, если известны гистерезисные зависимости исполь­зуемого материала.

§ 14.2 логических устройствах и устройствах, применяемых в вычислительной техни­ке. используют элементы, имеющие разветвленные магнитные цепи, выполненные из фер­рита с почти прямоугольной петлей гистерезиса (трансфлюксоры, биаксы, леддики и др ).

Изложенную в § 14.18 методику расчета, если ее несколько видоизменить, можно при­менить и при нахождении потокораспределения в упомянутых элементах в установившихся режимах работы. 8 этом случае расчет следует начинать с определения положения узлов магнитной цепи этого элемента (в таких элементах узлы, как правило, выражены в неяв­ном виде). Каждую ветвь следует представить как две параллельные со своими длинами и рассматривать их как самостоятельные ветви со своими потоками. Это необходимо по­тому, что магнитные потоки в двух параллельных участках каждой ветви могут замыкать­ся по различным путям. Например, магнитные потоки двух параллельных участков при определенных условиях могут замыкаться в пределах одной ветви. Расчет выполняют так же, как и в § 14.18. Однако ВАХ каждого участка должны быть взяты в виде прямоугольной (ромбовидной) петли с ис- ходящими из двух ее противоположных углов горизонталь- ными (почти горизонтальными) прямыми. Для каждого со- Ц\\

четания МДС (они могут и отсутствовать) будет по крайней /Тхх—\

мере по два решения, так как ВАХ имеют петлевую форму. J I [р ) Л»ф) ГI

§ 14.3 число узлов магнитной цепи больше двух, то по- I /\ \\-._/ /

токораспределение в ней можно найти методом постепенно- V \ I ]

го приведения ее к магнитной цепи с двумя узлами. Так. в х/*'—

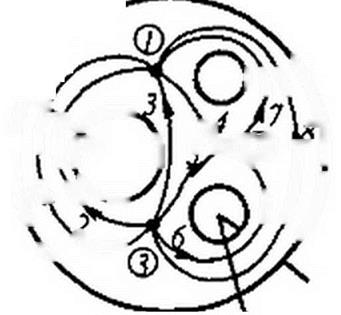
трехотверстном трансфлюксоре (рис. 14.17) цифры я круж- ках /. 2, 3 означают узлы. Восемь тонких линий — это сред- ние магнитные линии ветвей. Стрелки на них указывают про­извольно выбранные направления потоков. Провода стока- Рис. 14.17

ми /, и /₂ проходят через отверстия трансфлюксора.

Сначала строим зависимость суммы потоков ветвей 5 и б от магнитного напряжения между узлами 3 и 2, учитывая ток Затем строим зависимость Ф_{4 2} = /((/_м2।). Имея

в виду, что Ф₅₆=Ф₄₇, суммируем абсциссы полученных кривых и находим Ф$,б После этого задача оказывается сведенной к задаче с двумя узлами —

1 и 3. В более сложных задачах можно воспользоваться методом, рассмотренным в [24].

§ 14.4 дика расчета разветвленных магнитных цепей в историческом плане развива­лась постепенно и усовершенствовалась по мере возникновения новых практических за­дач. Сначала расчет проводили, используя магнитные сопротивления участков магнитной цепи /?_м (см. § 14.23). Однако ввиду того что R_M является нелинейной функцией маг­нитного потока, который перед проведением расчета неизвестен, на второй стадии пере­шли к расчету магнитных цепей с использованием однозначных нелинейных ВАХ (см. § 14.13). Впоследствии появилась необходимость использовать петлевые зависимос­ти потоков от магнитных напряжений. В настоящее время при расчете магнитных цепей, работающих при больших скоростях перемагничивания, оказывается необходимым не толь­ко принимать во внимание зависимость магнитного состояния от предшествующих про­цессов намагничивания, но и учитывать магнитную вязкость и поверхностный эффект (см. § 16.14).

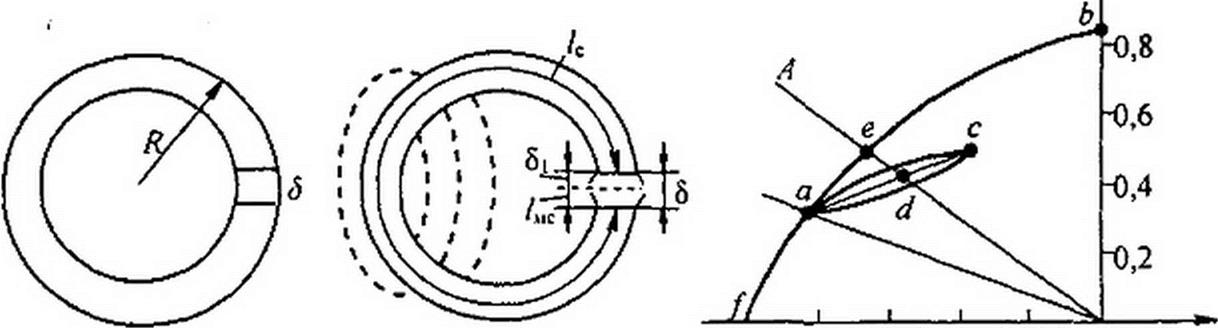
§ 14.20 Получение постоянного магнита. Возьмем замкнутый коль­цевой сердечник из магнитотвердого материала. Сделаем в нем два очень тонких (бесконечно тонких) радиальных пропила на расстоянии 5 (рис. 14.18, а). Выпиленный кусок оставим пока на месте. Затем намо-

И. Тл

-6000 -2000 0 МА/м

а б в

Рис. 14.18

таем на сердечник обмотку и пропустим по ней такой ток, чтобы намаг­нитить сердечник до насыщения. После этого ток выключим и обмотку смотаем. Сердечник оказывается намагниченным. Намагниченность его есть следствие того, что магнитные моменты областей самопроизволь­ного намагничивания сохранили свою ориентацию, вызванную предше­ствующим воздействием внешнего поля.

Магнитный поток в теле сердечника определяется суммой магнитных моментов всего сердечника. Удалим выпиленный кусок (рис. 14.18, б). Объем намагниченного вещества уменьшится на объем вынутой части. Кроме того, магнитному потоку придется проходить через воздушный зазор. Все это приведет к уменьшению магнитного потока в теле сердеч­ника.

В воздушном зазоре сердечника при отсутствии на нем обмотки с током проходит магнитный поток — устройство представляет собой по­стоянный магнит.

§ 14.21 Расчет магнитной цепи постоянного магнита. Магнитная индукция в зазоре магнита (5₈) зависит от соотношения между длиной воздушного зазора 3 и длиной ферромагнитной части магнита Z_c (рис. 14.18, б). Обозначим: Н_ъ — напряженность поля в воздушном за­зоре; В_с — магнитная индукция в теле магнита; Н_с — напряженность магнитного поля в теле магнита.

Найдем две неизвестные величины — В_с и Н_с, полагая известными кривую размагничивания ферромагнитного материала, зазор 3 и длину /_с. Одна связь между ними (нелинейная) дается кривой размагничива­ния (рис. 14.18, в). Другая связь (линейная) следует из закона полного тока.

Действительно, если воспользоваться законом полного тока, то мож­но записать

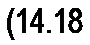■fw d! = Н_с l_c + H_s 5 = 0.

Нуль в правой части уравнения (14.18) объясняется тем, что на по­стоянном магните нет обмотки с током. Но = 0,8-10⁶ /?₈, где — в А / м, 2?₈ — в Тл.

Если зазор достаточно мал, то можно в первом приближении принять, что рассеяние потока отсутствует и В_с S_c = В₈ $₈, где S_c — площадь поперечного сечения магнита; S₅ — площадь поперечного сечения воз­душного зазора. Отсюда

в₅=г_с^-; Н₅=0,8-!0⁶ 5₅=О,8.1О⁶^5_?.

^5 ох

Подставив Z/₈ в уравнение (14.18), получим

Н_с = -N В_с, где

W = 0,8-10⁶-^.

'Л

Коэффициент N, зависящий от геометрических размеров, называют размагничивающим фактором"*’. [/V] = А • м / (В < с).

Для определения Н_с и В_с на рис. 14.18, в следует нанести прямую 0а, построенную по (14.19). В точке пересечения прямой с кривой раз­магничивания удовлетворяются обе связи между В_с и Н_с> которым дол­жно быть подчинено решение.

Приведенный расчет дает достаточно точный результат, если зазор д очень мал по сравнению с длиной /. Если это условие не выполнено, то значительная часть магнитных силовых линий замыкается, как показано пунктиром на рис. 14.18, б. В этом случае поток, индукция и напряжен-

*’Название коэффициента А' показывает, что с его помошью можно определить то раз­магничивание (уменьшение магнитного потока в теле магнита), которое происходит при введении воздушного зазора в магнитную цепь постоянного магнита.

кость вдоль сердечника изменяются. Это учитывают при расчете, вводя некоторые поправочные коэффициенты, определяемые из опыта.

Пример 144. Найти В_с, В₅, Н_с и Н_ь, если постоянный магнит (см. рис. 14.18, б) имеет /? = 5см, 8 = 1см. Кривая размагничивания изображена на рис. 14.18. в.

Решение. Если пренебречь боковым распором магнитных силовых линий в зазо- 10⁶ ,

ре, то 5б=5_с. При этом размагничивающий фактор W = 0,8-—-—- = 263-10. На

рис. 14.18, в проводим прямую 0а по уравнению Н_с =-263-Ю². Точка а ее пересечения с кривой размагничивания даст Д_с = 0,ЗТл и Н_с = -8000 А/м. Такая же индукция будет в воздушном зазоре. /У₅ = 0,8-10⁶-0.3 = 24-10⁴ А/м.

§ 14.22 Прямая и коэффициент возврата. Частично заполним за­зор 5 на длине /_мс (рис. 14.18, б) куском .магнитомягкого материала. Под действием поля постоянного магнита внесенный кусок намагнитится и поток в теле магнита возрастет.

Ввиду наличия гистерезиса магнитное состояние постоянного магнита будет изменяться не по участку ab (см. рис. 14.18, в) кривой размагни­чивания, а по нижней ветви adc частного цикла.

Для упрощения расчетов принято заменять частный цикл прямой ли­нией, соединяющей его вершины. Эту прямую линию ас называют пря­мой возврата.