Магнитная индукция — это векторная величина, определяемая по силовому воздействию_магнитного поля на ток (см. гл. 21).
Намагниченность J — магнитный момент единицы объема вещества.
Кроме этих двух величин магнитное поле характеризуется напряженностью магнитного поля Н.
Три величины — В, J, Н — связаны друг с другом следующей зависимостью"’:
£ = p0(//+J). (14.1)
В СИ единица индукции В — тесла (Тл): 1 Тл = 1 В-с/м2 = 1 Вб/м2, а в системе СГСМ — гаусс (1 Гс = 10‘8 Вб/см2).
Единица намагниченности J и напряженности поля Н — ампер на метр (А /м), а в системе СГСМ — эрстед (Э).
Намагниченность J представляет собой вектор, направление которого полагают совпадающим с направлением Н в данной точке:
(14.2)
’’Стрелка над буквой характеризует вектор в пространстве. Пояснения к формуле (14.1) см. в § 14.24.
Коэффициент % для ферромагнитных веществ является функцией Н. Подставив (14.2) в (14.1) и обозначив 1 + х = Ц,, получим
В = ц0»гН = раН, (14.3)
где ц0— постоянная, характеризующая магнитные свойства вакуума; ца— абсолютная магнитная проницаемость.
В СИ ц0 =4тс-10”7 Гн/м = 1,257-10-6 Гн/м; в СГСМ ц0 = 1. Для ферромагнитных веществ является функцией Н.
Магнитный поток Ф через некоторую поверхность 5 — это поток вектора магнитной индукции через эту поверхность:
(14.4)
где dS — элемент поверхности S.
В СИ единица магнитного потока — вебер (Вб); в СГСМ — максвелл (Мкс); 1Мкс = 10-8 Вб; 1кМкс = 103 Мкс.
При расчетах магнитных цепей обычно применяют две величины: магнитную индукцию В и напряженность магнитного поля Н.
Намагниченность J в расчетах, как правило, не используют (при необходимости значение J, отвечающее соответствующим значениям В и И, всегда можно найти по формуле (14.1)).
Ферромагнитные вещества имеют кристаллическую структуру. Каждый кристалл состоит из самопроизвольно намагниченных областей — доменов. Магнитное состояние каждого домена характеризуется вектором намагниченности. Решающую роль в формировании ферромагнитных свойств играет спиновый магнитный момент атома, обусловленный наличием нескомпенсированных спинов на одной из внутренних оболочек атома. В ферромагнетиках электроны одного атома расположены настолько близко к ядру другого атома, что между соседними атомами имеет место как бы обмен электронами. При этом между соседними атомами действуют не только магнитные силы, обусловленные взаимодействием спинов, но и силы, вызванные наличием обменных электронов. Последним соответствует обменная энергия (обменный интеграл).
Ферромагнитные свойства проявляются в том случае, когда обменный интеграл положителен. Обменные силы стремятся установить соседние атомы так, чтобы их магнитные моменты были параллельны, тогда как магнитные силы взаимодействия между соседними спинами стремятся установить соседние атомы так, чтобы их магнитные моменты были ан- типараллельны. Эти два взаимодействия определяют размер доменов.
В размагниченном в макросмысле теле при отсутствии внешнего поля векторы намагниченности доменов направлены неупорядоченно. При воздействии на тело внешнего магнитного поля по мере увеличения интенсивности последнего сначала возрастают объемы доменов, векторы намагниченности которых наиболее близки к вектору внешнего поля. Этот процесс, происходящий за счет соседних доменов, получил название «смещение границ». Затем ориентация доменов скачкообразно изме
няется в том направлении легкого намагничивания, которое ближе всего к направлению вектора внешнего поля («скачки Баркгаузена»). При дальнейшем увеличении интенсивности внешнего поля векторы намагниченности отдельных доменов поворачиваются по внешнему полю. Если ферромагнитное тело неоднородно по структуре, то эти три процесса могут происходить одновременно.
§ 14.3 Основные характеристики ферромагнитных материалов. Свойства ферромагнитных материалов принято характеризовать зависимостью магнитной индукции В от напряженности магнитного поля Н. Различают два основных типа этих зависимостей: кривые намагничивания и гистерезисные петли.
Под кривыми намагничивания понимают однозначную зависимость между В и И. Кривые намагничивания подразделяют на начальную, основную и без гистерезисную (что будет пояснено далее).
Из курса физики известно, что ферромагнитным материалам присуще явление гистерезиса — отставание изменения магнитной индукции В от изменения напряженности магнитного поля Н. Гистерезис обусловлен необратимыми изменениями энергетического состояния под действием внешнего поля И. При периодическом изменении напряженности поля зависимость между В и Н приобретает петлевой характер.
Различают несколько типов гистерезисных петель — симметричную, предельную и несимметричную (частный цикл).
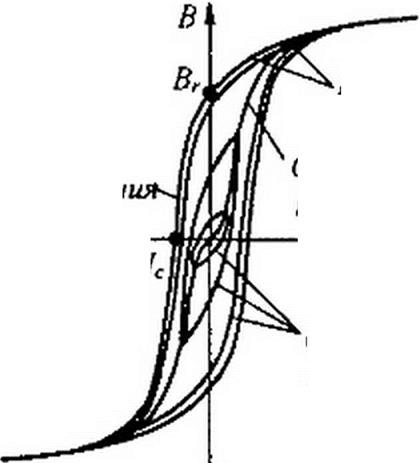
На рис. 14.1 изображено семейство симметричных гистерезисных петель. Для каждой симметричной петли максимальное положительное значение В равно максимальному отрицательному значению В и, соот- ветственно, Я„,ах =]-Нт„\.
 |
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
| ||||||||||
 | |||
 | |||
| ||||||
| ||||||
| ||||||
Геометрическое место вершин симметричных гистерезисных петель называют основной кривой намагничивания. При очень больших Н вблизи ±//тах восходящая и нисходящая ветви гистерезисной петли практически сливаются.
Предельной гистерезисной петлей, или предельным циклом, называют симметричную гистерезисную петлю, снятую при очень больших Нтах. Индукцию при Н = 0 называют остаточной индукцией и обозначают Вг.
Напряженность поля при В = 0 называют задерживающей или коэрцитивной силой и обозначают Нс.
Участок предельного цикла Вг Нс (см. рис. 14.1) принято называть кривой размагничивания или «спинкой» гистерезисной петли.
Этот участок используют при расчетах магнитных цепей с постоянными магнитами и магнитных элементов запоминающих устройств вычислительной техники.
Если изменять Н периодически и так, что +Нт&х ^|- /7тах|, то зависимость между В и Н будет иметь вид петли, но центр петли не совпадает с началом координат (рис. 14.2). Такие гистерезисные петли называют частными петлями гистерезиса или частными циклами.
Когда предварительно размагниченный ферромагнитный материал (В = О, Н = 0 ) намагничивают, монотонно увеличивая Н, получаемую зависимость между В и Н называют начальной кривой намагничивания.
Начальная и основная кривые намагничивания настолько близко расположены друг к другу, что практически во многих случаях их можно считать совпадающими (см. рис. 14.2).
Безгистерезисной кривой намагничивания называют зависимость между В и //, возникающую, когда при намагничивании ферромагнитного материала его периодически постукивают или воздействуют на него полем, имеющим кроме постоянной составляющей еще и затухающую по амплитуде синусоидальную составляющую. При этом гистерезис как бы снимается.
Безгистерезисная кривая намагничивания резко отличается от основной кривой.
В различных справочниках, а также в ГОСТе в качестве однозначной зависимости между В и Н дается основная кривая намагничивания.
§ 14.4 Потери, обусловленные гистерезисом. При периодическом перемагничивании ферромагнитного материала в нем совершаются необратимые процессы, на которые расходуется энергия от намагничивающего источника. В общем случае потери в ферромагнитном сердечнике обусловлены гистерезисом, макроскопическими вихревыми токами и магнитной вязкостью. Степень проявления различных видов потерь зависит от скорости перемагничивания ферромагнитного материала. Если сердечник перемагничивается во времени замедленно, то потери в сердечнике обусловлены практически только гистерезисом (потери от макроскопических вихревых токов и магнитной вязкости при этом стремятся к нулю).
Физически потери, обусловленные гистерезисом, вызваны инерционностью процессов роста зародышей перемагничивания, инерционностью процессов смещения доменных границ и необратимыми процессами вращения векторов намагниченности.
Площадь гистерезисной петли dB характеризует энергию, выделяющуюся в единице объема ферромагнитного вещества за один цикл перемагничивания.
Представим площадь гистерезисной петли (рис. 14.3) в виде суммы четырех площадей: jН dВ = S} + S2 + Sy + S4.
Площадь S] соответствует движению от точки / до точки 2; так как на зтом участке Н >0 и dB>0, то произведение Н dB>Q и S, > 0. Площадь 52 характеризует движение от точки 2 до точки 3; так как в этом интервале Н > 0 и dB <0, то $2<0. Площадь — движение отточки 3 до точки 4; так как Н < 0 и dB < 0, то 53 > 0. Площадь — движение от точки 4 до точки /; так как Н <0 и dB>Q, то S4 < 0.
Если ферромагнитный сердечник подвергается периодическому намагничиванию (например, в цепях переменного тока), то для уменьшения потерь на гистерезис в нем он должен быть выполнен из магнитомягкого материала (см. § 14.5).
§ 14.5 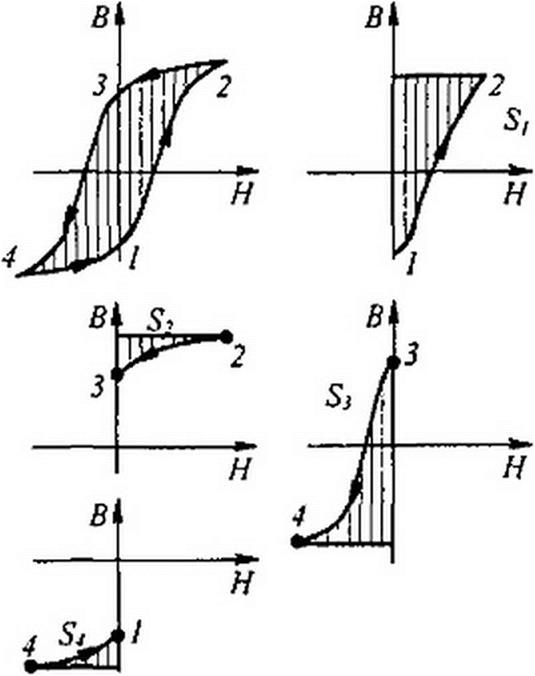
|
Магнитомягкие и магнитотвердые материалы. Ферромагнитные материалы подразделяют на магнитомягкие и магнитотвердые.
Магнитомягкие материалы обладают круто поднимающейся основной кривой намагничивания и относительно малыми площадями гистерезисных петель. Их применяют во всех устройствах, которые работают или могут работать при периодически изменяющемся магнитном потоке (трансформаторах, электрических двигателях и генераторах, индуктивных катушках и т.п.).
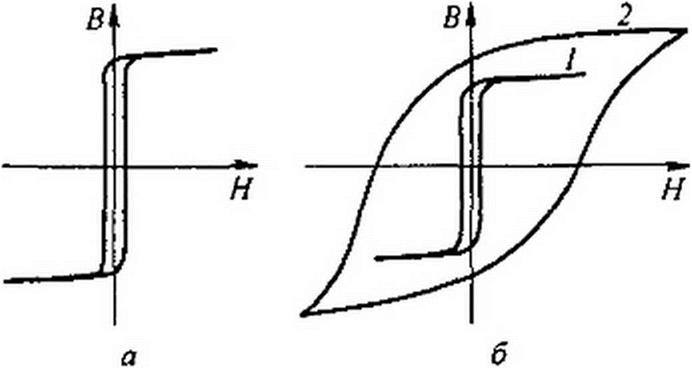
Некоторые магнитомягкие материалы, например перминвар, сплавы 68НМП и др., обладают петлей гистерезиса по форме, близкой к прямоугольной (рис. 14.4, п). Такие
материалы получили распространение в вычислительных устройствах и устройствах автоматики.
В группу магнитомягких материалов входят электротехнические стали, железоникелевые сплавы типа пермаллоя и др.
|
Магнитотвердые материалы обладают полого поднимающейся основной кривой
намагничивания и большой площадью гистерезисной петли. В группу
магнитотвердых материалов входят углеродистые стали, сплавы магни- ко, вольфрамовые, платино-кобальтовые сплавы и сплавы на основе ред- поземельных элементов, например самарий-кобальтовые. У последних Вг ® 0,9 Тл и Нс = 660 кА / м.
На рис. 14.4, б качественно сопоставлены гистерезисные петли для магнитомягкого материала типа пермаллоя (кривая /) и для магнитотвердого материала (кривая 2).
§ 14.6 Магнитодиэлектрики и ферриты. В радиотехнике, где используют колебания высокой частоты, сердечники индуктивных катушек изготовляют из магнитодиэлектриков или ферритов.
Магнитодиэлектрики — материалы, полученные смешением мелко- измельченного порошка магнетита, железа или пермаллоя с диэлектриком. Эту смесь формуют и запекают. Каждую ферромагнитную крупинку обволакивает пленка из диэлектрика. Благодаря наличию таких пленок сердечники из магнитодиэлектриков не насыщаются; их находится в интервале от нескольких единиц до нескольких десятков.
Ферриты — ферримагнитные материалы. Магнитомягкие ферриты изготовляют из оксидов железа, марганца и цинка или из оксидов железа, никеля и цинка. Смесь формуют и обжигают, в результате получают твердый раствор. По своим электрическим свойствам ферриты являются полупроводниками. Их объемное сопротивление р - 1 -J-107 Ом • м, тогда как для железа р » 10"6 Ом • м.
Можно получить ферриты с различными магнитными свойствами. В отличие от магнитодиэлектриков ферриты могут насыщаться. Коэрцитивная сила магнитомягких ферритов составляет примерно 10 А /м. Маркируют их буквами и цифрой. Например, феррит 6000 НМ означает никель-марганцевый феррит, у которого на начальном участке кривой намагничивания |ir=6000. Магнитотвердые ферриты выполняют на основе феррита бария. Например, у феррита ЗБА Вг=0,38Тл; //с-145А/м.
§ 14.7 Закон полного тока. Магнитное поле создается электрическими токами. Количественная связь между линейным интегралом от вектора напряженности магнитного поля Н вдоль любого произвольного контура и алгебраической суммой токов £ /, охваченных этим контуром, определяется законом полного тока:
= (14.5)
Положительное направление интегрирования dl связано с положительным направлением тока / правилом правого винта. Если контур интегрирования будет проходить внутри катушки с числом витков w, по которой протекает ток /, то
^2 Z = / w и dl - I и:
Закон полного тока является опытным законом. Его можно экспериментально проверить путем измерения <р/ dl с помощью специального устройства (известного из курса физики), называемого магнитным поясам.
§ 14.8 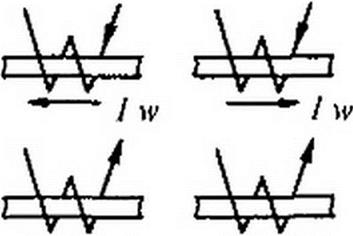
|
|
Магнитодвижущая (намагничивающая) сила. Магнитодвижущей силой (МДС), или намагничивающей силой (НС), катушки или обмотки с током называют произведение числа витков катушки w на протекающий по ней ток /.
МДС / w вызывает магнитный поток в магнитной цепи подобно тому, как ЭДС вызывает электрический ток в электрической цепи. Как и ЭДС, МДС — величина направленная (положительное обозначают стрелкой).
Положительное направление МДС совпадает с движением острия правого винта, если винт вращать по направлению тока в обмотке.
Для определения положительного направления МДС пользуются мнемоническим правилом', если сердечники мысленно охватить правой рукой, расположив ее пальцы по току в обмотке, а затем отогнуть большой палец, то последний укажет направление МДС.
На рис. 14.5 дано несколько эскизов с различным направлением намотки катушек на сердечник и различным направлением МДС.
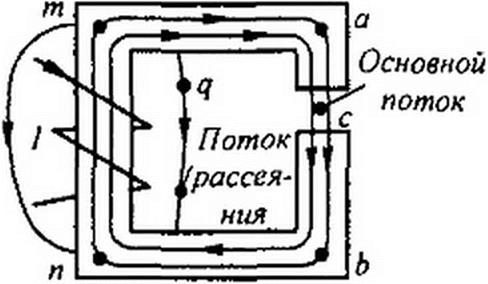
§ 14.9 Разновидности магнитных цепей. Магнитной цепью в общем случае называют совокупность катушек с током, ферромагнитных тел или каких-либо иных тел (сред), по которым замыкается магнитный поток.
 |
|
 |
|
|
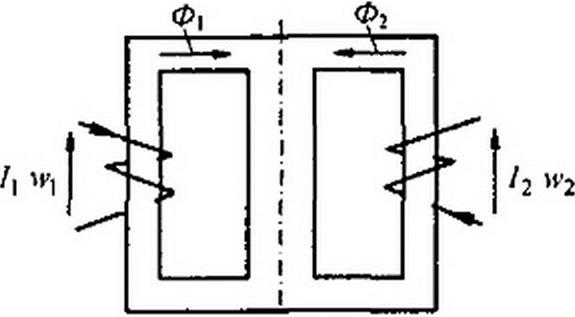
Магнитные цепи могут быть подразделены на неразветвленные и разветвленные. Примером неразветвленной цепи может служить цепь, показанная на рис. 14.6. Разветвленные цепи делятся на симметричные и несимметричные. Магнитная цепь на рис. 14.7 симметрична: в ней
Ф( = Ф2, если обе части ее, расположенные слева и справа от вертикальной пунктирной линии, одинаковы в геометрическом отношении, изготовлены из одного и того же материала и если /t wj = /2 и>2.
Достаточно сделать /, w, * /2 vv2, изменить направление тока в одной из обмоток или сделать воздушный зазор в одном из крайних стержней магнитопровода, чтобы магнитная цепь (рис. 14.7) стала несимметричной. Если цепь (см, рис. 14.7) окажется несимметричной, то Ф| * Ф2.
§ 14.10 Роль ферромагнитных материалов в магнитной цепи.
Электрические машины, трансформаторы и другие аппараты конструируют так, чтобы магнитный поток в них был по возможности наибольшим. Если в магнитную цепь входит ферромагнитный материал, то поток в ее ветвях при одной и той же МДС и одинаковой геометрии цепи оказывается во много раз больше, чем в случае отсутствия ферромагнитного материала.
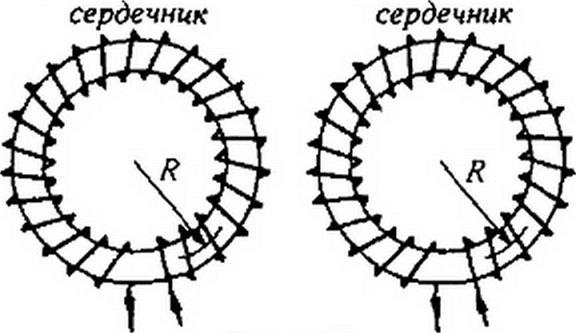
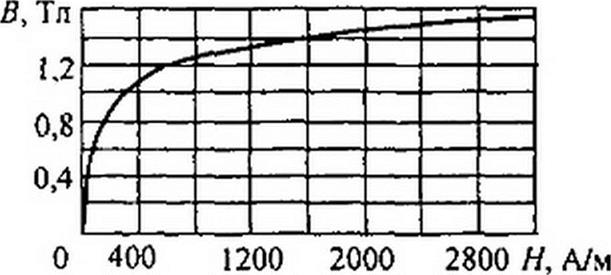
Пример 139. Даны два одинаковых в геометрическом отношении кольцевых сердечника (рис. 14.8). Радиус их средней магнитной линии /? = 11см, поперечное сечение 5 = 2 см2. Один сердечник неферромагнитный, например деревянный, а другой — ферромагнитный (кривая намагничивания представлена на рис. 14.9). На каждый кольцевой
 |
| ||||
| ||||
 |
|
сердечник намотана обмотка с числом витков = 200 и через них пропущен одинаковый ток / = 1 А. Определить потоки в сердечниках.
Р е ш е н и е. По закону полного тока, напряженность поля одинакова в обоих сердечниках и не зависит от материала:
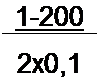 | |||
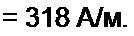 | |||
Магнитный поток а неферромагнитном сердечнике
Ф1)ф = В S = р0 ц W S = 1.257-10-6-318-2■ Ю"4 =8-10~8 Вб.
По кривой намагничивания (рис. 14.9) находим, что при Н = 318А/м В = 1,02Тл. Магнитный поток в ферромагнитном сердечнике
Ффм = £ S = 1,02-Ю“4-2 = 20.410'5 Вб.
Таким образом, поток в ферромагнитном сердечнике в 2550 раз больше, чем в нефер- ромагнитяом.
Ферромагнитные материалы вводят в магнитную цепь также с целью сосредоточения магнитного поля в заданной области пространства и придания ему определенной конфигурации.
§ 14.11 Падение магнитного напряжения. Падением магнитного напряжения между точками а и b магнитной цепи называют линейный интеграл от напряженности магнитного поля между этими точками:
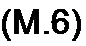 Ум а» = Jw dl.
Ум а» = Jw dl.
а
Если на этом участке Н ^постоянна и совпадает по направлению с элементом пути dl, то Н dl = Н dl cosO° и Н можно вынести из-под знака интеграла. Тогда
h
~ & \dl ~ Н lab’ (1^.7)
а
где 1аЬ — длина пути между точками а и Ь.
Единица падения магнитного напряжения — ампер (А).
В том случае, когда участок магнитной цепи между точками а и b может быть подразделен на п отдельных частей так, что для каждой части Н - Нк = const, то
п
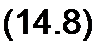 ^МаЬ=ХНк^
^МаЬ=ХНк^
к=1
§ 14.12 Вебер-амперные характеристики. Под вебер-алтерпой (максвелл-амперной) характеристикой (ВАХ)Ф) понимают зависимость потока Ф по какому-либо участку магнитной цепи от падения магнитного напряжения на этом участке: Ф - Она также важна при расчетах и исследовании магнитных цепей, как и ВАХ нелинейных сопротивлений при расчетах и исследовании электрических цепей с нелинейными резисторами (см. гл. 13).
ВАХ при расчетах магнитных цепей в готовом виде на задаются. Перед расчетом их нужно построить с помощью кривых намагничивания ферромагнитных материалов, входящих в магнитную цепь.
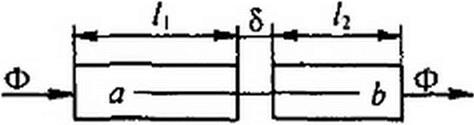
§ 14.13 Построение вебер-амперных характеристик. Парис. 14.10 изображен участок магнитной цепи, по которому проходит поток Ф. Пусть участки /г и /2 сечением 5 выполнены из ферромагнитного материала, кривая В = f(H) для которого дана на рис. 14.9. На участке длиной 5 магнитный поток проходит по воздуху. Требуется построить ВАХ участка цепи между точками а и Ь.
При построении допустим, что:
1) магнитный поток вдоль всего участка от а до b постоянен (отсутствует рассеяние);
2) сечение магнитного потока в воздушном зазоре такое же, как и на участках и /2 (отсутствует боковой распор силовых линий в зазоре).
В действительности оба допущения справедливы лишь в известной мере и чем больше воздушный зазор, тем менее они выполняются.
Построение ВАХ производим следующим образом. Задаемся рядом значений индукции В, например для электротехнических сталей 0; 0,5; 0,8; 1,0; 1,1; 1,2; 1,3; 1,4; 1,5 Тл, и для каждого значения В находим напряженности поля на всех участках Z2 и 6.
На участках из ферромагнитного материала (/, и /2) напряженность Н1 = Н2 (так как #1 = #2) определяем по кривой намагничивания.
пВ гл. 14 (в отличие от гл. 13) под ВАХ понимается вебер-ампсрная характеристика.
Для неферромагнитных участков (участок 5)
=-------------- ^0,8-Ю6 В,
Ио 1,256-10"6
где Н — в А/м; В — в Тл; р0 — в Гн / м.
Таким образом, для определения Н в воздухе следует умножить индукцию, выраженную в теслах, на коэффициент 0,8-106.
Для каждого значения В вычисляем поток и находим
~ Н\ h + #2 6 + ^5 $•
По результатам подсчетов строим кривую Ф = /((7М).
|
Пример 140. Построить ВАХ для участка цепи (рис. 14.10) при 8 = 0; 0,005; 0,05 см; /}=10см; А = 5 см; 5 = 5 см2.
Решение. Определим падение магнитного напряжения между точками а и b участка магнитной цепи (см. рис. 14.10) при 8 = 0,005см и В=0,5Тл.
Из кривой (см. рис. 14.9) находим, что индукции В = 0,5Тл соответствует напряженность поля
# = 40А/м. Таким образом, при 5 = 0,5Тл = Н2 = 40 А/м.
Падение напряжения между точками а и b
U„ab s А +Н2/2 + ^ь S = 40-0,1 + 40 0,05 +0,8 0.5-106 • 5-Ю-5 = 26 А.
Значения UMab при иных зазорах и индукциях рассчитываем аналогичным образом (табл. 14.1).
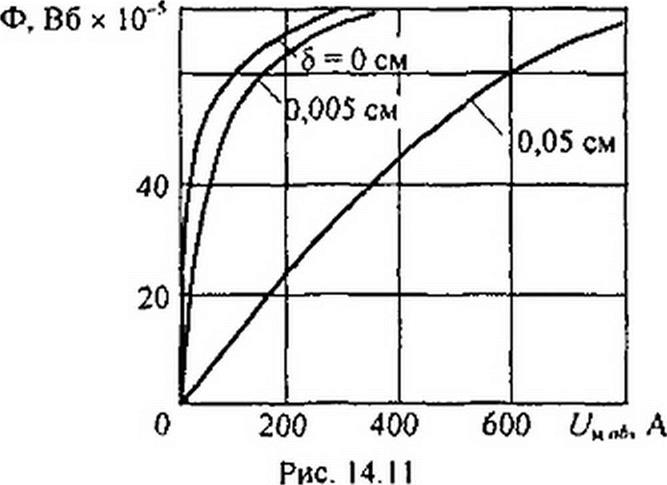 |
Таблица 14.1
| В.Тл | Ф. Вб • 10’5 | /Л = Н2, А / м | /А, А/м - 10’ | САм, А, при 8. см | ||
| 0 | 0.005 | 0,05 | ||||
| 0.5 | 25 | 40 | 4 | 6 | 26 | 206 |
| 0.8 | 40 | 130 | 6.4 | 19.5 | 51,5 | 339,5 |
| 1.0 | 50 | 300 | 8 | 45 | 85 | 445 |
| 1.1 | 55 | 440 | 8.8 | 66 | 110 | 506 |
| 1.2 | 60 | 700 | 9.6 | 105 | 153 | 585 |
| 1,3 | 65 | 1080 | 10.4 | 162 | 214 | 682 |
| 1,4 | 70 | 1800 | 11.2 | 270 | 326 | 830 |
По данным табл. 14.1 построены ВАХ при трех значениях 5 (рис. 14.11). Из построений видно, что если участок, для которого строят ВАХ, не имеет «воздушного» включения, то ВАХ круто поднимается вверх. При наличии воздушного включения ВАХ спрямляется и идет более полого.
§ 14.14 Законы Кирхгофа для магнитных цепей. При расчетах магнитных цепей, как и электрических, используют первый и второй законы (правила) Кирхгофа.








