Нелинейные электрические цепи

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

ПОСТОЯННОГО ТОКА

§ 1.2 Основные определения. Как уже говорилось 8 § 2.1, под нелинейными электрическими цепями принято понимать электрические цепи, содержащие нелинейные элементы. Нелинейные элементы подраз­деляют на резистивные, индуктивные и емкостные.

Нелинейные резисторы (HP), в отличие от линейных, обладают нели­нейными вольт-амперными характеристиками. Напомним, что вольт-ам­перная характеристика (ВАХ) — это зависимость тока, протекающего через резистор, от напряжения на нем. Нелинейные резисторы могут быть подразделены на две большие группы: неуправляемые и управляемые.

В управляемых HP, в отличие от неуправляемых, кроме основной цепи, как правило, есть еще по крайней мере одна вспомогательная или управляющая цепь, воздействуя на ток или напряжение которой можно деформировать ВАХ основной цепи. В неуправляемых HP ВАХ изображается одной кривой, а в управляемых — семейством кривых.

В группу неуправляемых HP входят лампы накаливания, электрическая дуга, бареттер, газотрон, стабиловольт, тиритовые сопротивления, полу­проводниковые выпрямители (диоды) и некоторые другие.

В группу управляемых HP входят трехэлектродные (и более) лампы, транзисторы, тиристоры, терморезисторы, фоторезисторы, фотодиоды, магниторезисторы, магнитодиоды, магнитотранзисторы и другие эле­менты.

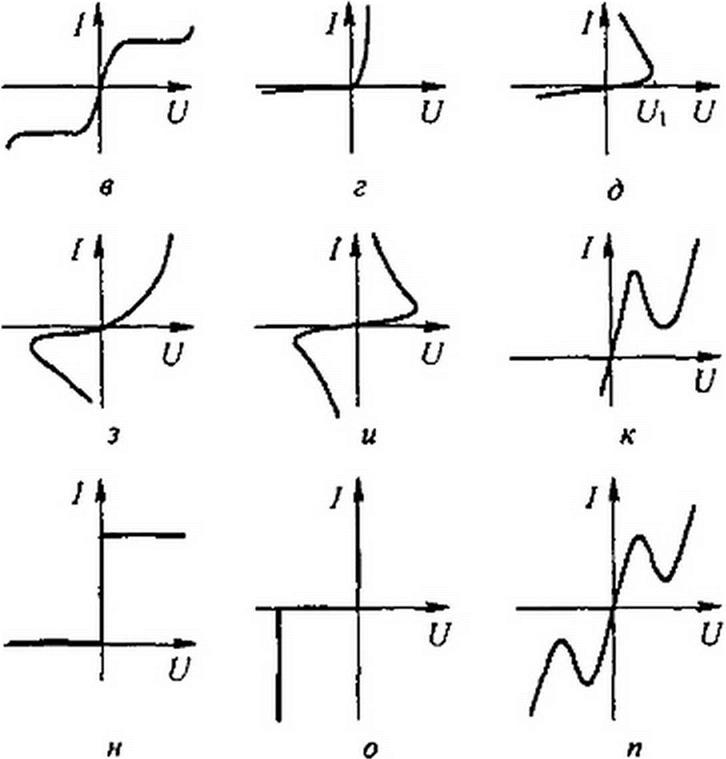
§ 1.3 ВАХ нелинейных резисторов. На рис. 13.1 изображено четыр­надцать типов наиболее часто встречающихся ВАХ неуправляемых ре­зисторов.

ВАХ на рис. 13.1, а имеют, например, лампы накаливания с металли­ческой нитью. Чем больше протекающий через нить ток, тем сильнее нагревается нить и тем больше становится ее сопротивление.

Если величину, откладываемую по оси абсцисс, обозначить х, а вели­чину, откладываемую по оси ординат, /(х), то характеристика рис. 13.1, а подчиняется условию

/(*) = -/(-*)•

Нелинейные резисторы, для которых выполняется это условие, назы­вают HP с симметричной вольт-амперной характеристикой.

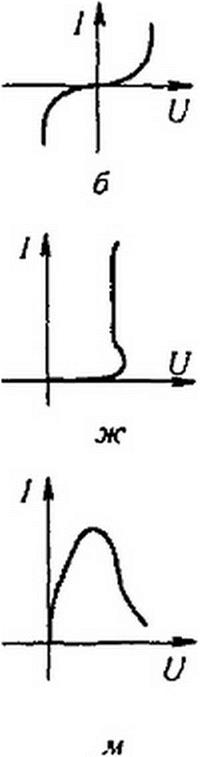
ВАХ на рис. 13.1, б обладают варисторы, некоторые типы терморези­сторов и лампы накаливания с угольной нитью. Для данной группы характерно, что с увеличением протекающего тока сопротивление их уменьшается. ВАХ их симметрична.

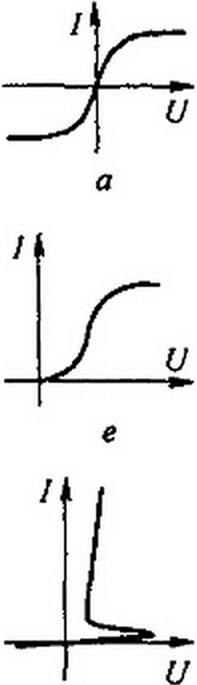ВАХ на рис. 13.1, в обладает, например, бареттер. Бареттер выполня­ют в виде спирали из стальной проволоки, помещенной в стеклянный сосуд, заполненный водородом при давлении порядка 80 мм рт. ст. В определенном диапазоне изменения тока ВАХ бареттера расположена почти горизонтально. Бареттер используют, например, для стабилизации тока накала электронных ламп при изменении напряжения питания. ВАХ на рис. 13.1, в также симметрична.

ВАХ на рис. 13.1, г, в отличие от предыдущих, несимметрична. Ею обладают полупроводниковые диоды (кремниевые, германиевые), широко применяемые для преобразования переменного тока в постоянный. Они способны пропускать ток практически только в одном, проводящем направлении. Широко используют их также в различных датчиках и пре­образователях устройств автоматики.

ВАХ на рис, 13.1, д имеют электрическая дуга с разнородными элек­тродами, газотрон и некоторые типы терморезисторов. Если напряжение повышать начиная с нуля, то сначала ток растет, но остается весьма ма­лым, после достижения напряжения (7, (напряжения зажигания) проис­ходит резкое увеличение тока в цепи и снижение напряжения на элект­рической дуге или газотроне. Для верхнего участка ВАХ приращению тока соответствует убыль напряжения на нелинейном сопротивлении.

Участок ВАХ типа верхнего участка кривой рис. 13.1, д называется падающим участком вольт-амперной характеристики \

Электрическую дугу широко применяют при сварке металлов, в элек­тротермии (в дуговых электропечах), а также в качестве мощного источ­ника электрического освещения, например в прожекторах.

Падающий участок ВАХ представляет собой такой ее участок, на котором положи­тельному приращению тока через HP соответствует отрицательное приращение напряже­ния иа нем.

Газотрон представляет собой лампу с двумя электродами, заполнен­ную благородным газом (неоном, аргоном и др.) или парами ртути.

ВАХ на рис. 13.1, е имеет двухэлектродная выпрямительная лампа — кенотрон. По нити накала лампы пропускают ток. Этот ток разогревает катод (один из двух электродов лампы) до высокой температуры, в ре­зультате чего с поверхности катода начинается термоэлектронная эмис­сия. Под действием электрического поля поток электронов направляется ко второму, холодному, электроду — аноду. В начальной части ВАХ за­висимость тока от напряжения подчиняется закону трех вторых: / = a u^i/2. ВАХ кенотрона несимметрична, это объясняется тем, что по­ток электронов направляется с катода на анод только в том случае, если анод положителен по отношению к катоду.

ВАХ на рис. 13.1, ж обладают лампы с тлеющим разрядом. К числу их относятся стабиловольты (стабилитроны) и неоновые лампы. При тлеющем разряде благородный газ, которым заполнена лампа, светится. ВАХ на рис. 13.1, ж свидетельствует о том, что в определенном диапа­зоне значений токов напряжение на лампе остается практически неизмен­ным.

Некоторые типы точечных германиевых и кремниевых диодов имеют ВАХ на рис. 13.1, з.

Электрическая дуга между электродами, выполненными из одного и того же материала и находящимися в одинаковых условиях, имеет ВАХ подобную приведенной на рис. 13.1, и.

ВАХ четырехслойного германиевого (кремниевого) диода — динис- тора — изображена на рис. 13.1, л; ВАХ туннельного диода — на рис. 13.1, к (о принципах работы тринистора см. § 15.43 и туннельного диода см., например, [20]).

ВАХ лямбда-диода изображена на рис, 13.1,.w, ВАХ диодного огра­ничителя тока — на рис. 13.1, н и ВАХ полупроводникового стабилиза­тора тока — на рис. 13.1, о. На рис. 13.1, п — ВАХ двух одинаковых встречно включенных туннельных диодов. ВАХ управляемых нелиней­ных элементов рассмотрены в гл. 15.

§ 1.4 Общая характеристика методов расчета нелинейных элек­трических цепей постоянного тока. В гл. 13 рассматривается методи­ка расчета простейших нелинейных электрических цепей с последова­тельно, параллельно и последовательно-параллельно соединенными HP и источниками ЭДС. Кроме того, изложена методика расчета сложных цепей, в основу которой положена диакоптика.

Обратим внимание на то, что с линейной частью любой сложной разветвленной цепи, содержащей HP, можно осуществлять любые пре­образования, рассмотренные в гл. I, если они облегчают расчет всей сложной схемы. Одно из таких преобразований — от треугольника сопротивлений к звезде для облегчения нахождения входного сопротив­ления линейной части схемы — использовано при расчете в § 13.9.

Из методов расчета, приведенных в гл, 1, к нелинейным цепям при­менимы следующие: метод двух узлов; замена нескольких параллельно
включенных ветвей одной эквивалентной; метод эквивалентного генера­тора и диакоптики и др.

До проведения расчета нелинейных цепей должны быть известны ВАХ HP, входящих в схему. Расчет нелинейных цепей постоянного тока производят, как правило, графически. Могут применяться и ЭВМ.

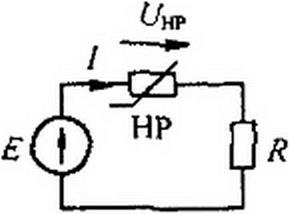
§ 1.5 Последовательное соединение HP. На рис. 13.2, а изображе­на схема последовательного соединения HP с заданной ВАХ, линейного сопротивления R и источника ЭДС Е.

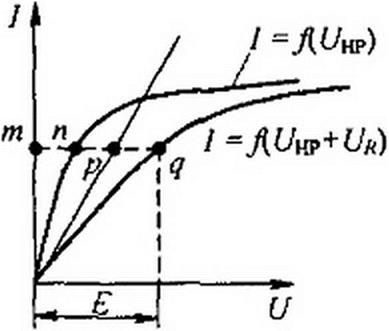
Требуется найти ток в цепи. ВАХ HP обозначена на рис. 13.2, б как / = ВАХ линейного сопротивления — прямая линия. ВАХ всей

цепи, т. е. зависимость тока в цепи от суммы падений напряжений на HP и R, обозначена через I ~ /(С/_нс + С^). Расчет основывается на законах Кирхгофа. Обсудим два способа расчета. Первый способ иллюстрирует рис. 13.2, б, второй — рис. 13.2, в.

При расчете цепи по первому способу строим результирующую ВАХ всей пассивной части схемы, исходя из того, что при последовательном соединении через HP и R проходит одинаковый ток. Для построения ре­зультирующей ВАХ задаемся произвольным током — точкой т, прово­дим через нее (рис. 13.2, б) горизонталь и складываем отрезок тп, рав­ный напряжению на HP, с отрезком тр, равным напряжению на R\ — —₄₎

тп + т р = т q .

Тогда q принадлежит результирующей ВАХ всей схемы. Аналогично строят и другие точки результирующей ВАХ. Определение тока в цепи при заданной ЭДС £ выполняют графически по результирующей ВАХ. С этой целью следует заданное значение ЭДС £ отложить по оси абсцисс и через полученную точку провести вертикаль до пересечения с резуль­тирующей ВАХ в точке q. Ордината точки q равна искомому току.

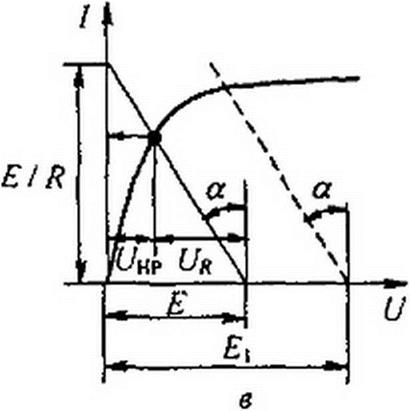
При расчете цепи по второму способу нет необходимости строить результирующую ВАХ пассивной части схемы. Учитывая, что уравнение I R + (7_НР = £ в координатах / и (7_НР представляет собой уравнение пря­мой, проходящей через точки l-E/R\ U=U_Hp~0', / = 0;

*' Здесь и далее черта над отрезком означает, что речь идет о его длине.

(/_HP = U = Е, проводим на рис. 13.2, в эту прямую. Тангенс угла а на* клона ее к вертикали, умноженный на отношение т_и! т, масштабов по осям, численно равен R.. Точка пересечения прямой с ВАХ HP опреде­ляет режим работы цепи. Действительно, для этой точки ток, проходя­щий через HP и /?, одинаков, а сумма падений напряжений t/_HP + U_R - Е. При изменении ЕДС от£ до Е_{ прямую / = f(U_к) следует переместить параллельно себе так, чтобы она исходила из точки I = О, U = Е_} (штри­ховая линия на рис. 13.2, в).

Аналогично рассчитывают цепи при последовательном соединении двух и большего числа HP. В этом случае сначала находят ВАХ двух HP, затем трех и т. д.

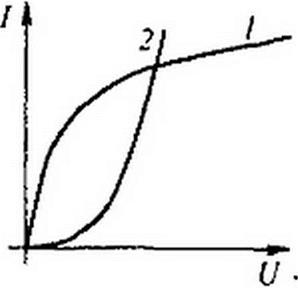
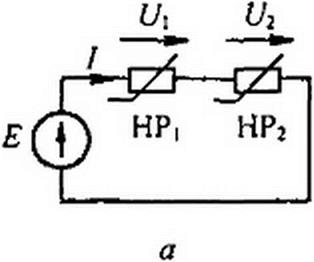
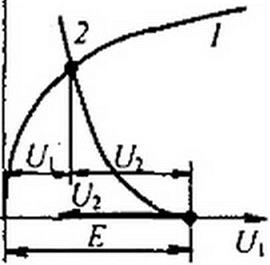
Обсудим применение второго способа для расчета цепи (рис. 13.3, а) с двумя различными HP. ВАХ И?! и НР₂ изображены на рис. 13.3, б. Так как НР₂ имеет нелинейную ВАХ, то вместо прямой / = j\U_л), как это было на рис. 13.2, в, теперь нужно построить нелинейную зависимость 1 - Начало ее (рис. 13.3, в) расположено в точке / = О, Ц = Е. Отсчет положительных значений (А ведется влево от этой точки. Так как положительные значения U₂ на рис. 13.3, б откладываем вправо от начала координат, а на рис. 13.3, в — влево, то кривая I - f(U₂) на рис. 13.3, в представляет собой зеркальное отображение кривой 2 (рис. 13.3, 0 относительно вертикальной оси, проведенной через точку U_} - Е.

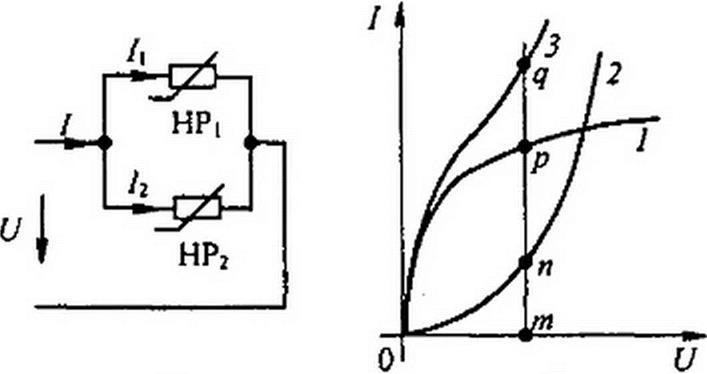
§ 1.6 Параллельное соединение HP. Схема параллельного соеди­нения двух HP изображена на рис. 13.4, а\ ее ВАХ — на рис. 13.4, б. При построении результирующей ВАХ исходят из того, что напряжение на HP_t и НР₂ равны в силу их параллельного соединения, а ток в нераз- ветвленной части схемы / = /, + /₂.

Кривая 3 на рис. 13.4, б представляет собой ВАХ параллельного соединения. Строим ее следующим образом. Задаемся произвольно на­пряжением U, равным отрезку От. Проводим через точку т вертикаль. Складываем отрезок тп, равный току в НР₂, с отрезком тр, равным току в НР|: тп + тр = тд.

Отрезок mq равен току в неразветвленной части цепи при напряже­нии От. Аналогично определяют и другие точки результирующей ВАХ параллельного соединения.

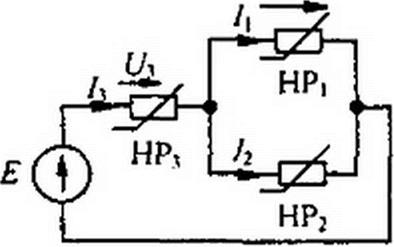
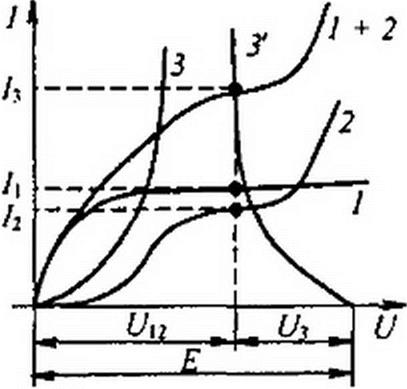
§ 1.7 Последовательно-параллельное соединение сопротивлений. На рис. 13.5, а изображена схема последовательного соединения НР₃ и двух параллельно соединенных HP, и НР₂. Требуется найти токи в вет­вях схемы. Заданы ВАХ нелинейных резисторов (кривые /, 2, 3 на рис. 13.5, б) и ЭДС Е. Сначала строим ВАХ параллельного соединения в соответствии с методикой, рассмотренной в § 13.5 (кривая 1 + 2 на рис. 13.5, б). После этого цепь сводится к последовательному соедине­нию НР₃ и HP, имеющего ВАХ 1 + 2.

Рис. 13.5

Применяем второй способ построения (см. § 13.4). Кривая 3* (рис. 13.5, 6) представляет собой ВАХ НР₃, зеркально отраженную от­носительно вертикали, проведенной через точку U = Е. В точке пересе­чения кривой 3' с кривой 1 + 2 удовлетворяется второй закон Кирхго­фа: U₃ +U\2 = £• Сумма токов /, + /₂ = /₃.

§ 1.8 Расчет разветвленной нелинейной цепи методом двух узлов. Для схем, содержащих только два узла или приводящихся к ним, применяют метод двух узлов. Рассмотрим его на примере схемы

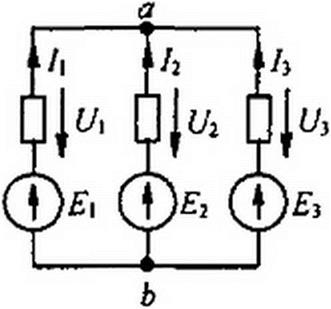
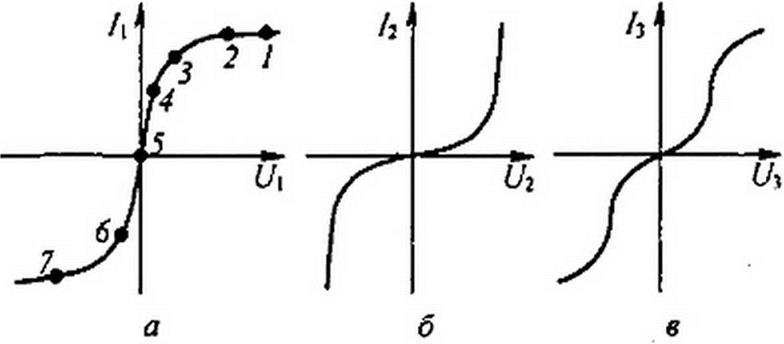
(рис. 13.6). В схеме три HP и три источника ЭДС. Пусть ВАХ HP изоб­ражаются кривыми (рис. 13.7, a-в). Для определенности положим, что £, > Е₂ > Е₃. Выберем положительные направления для токов. Пусть, например, все токи направлены к узлу а. Тогда, по первому закону Кирх­гофа,

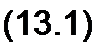/_l+/₂ + Z₃=O.

Каждый из токов является нелинейной функцией падения напряжения на своем HP. Так, 1_} является функцией (7,, /₂ — функцией U₂ и /₃ — функцией U₃.

Выразим все токи в функции одного переменного — напряжения U_ab между двумя узлами.

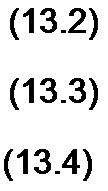Для этого выразим Ц, U₂, U₃ через ЭДС и U_ab :

U^E_}-U_ab;
U₂=E₂~U_ob‘_t
U^-U_oh.

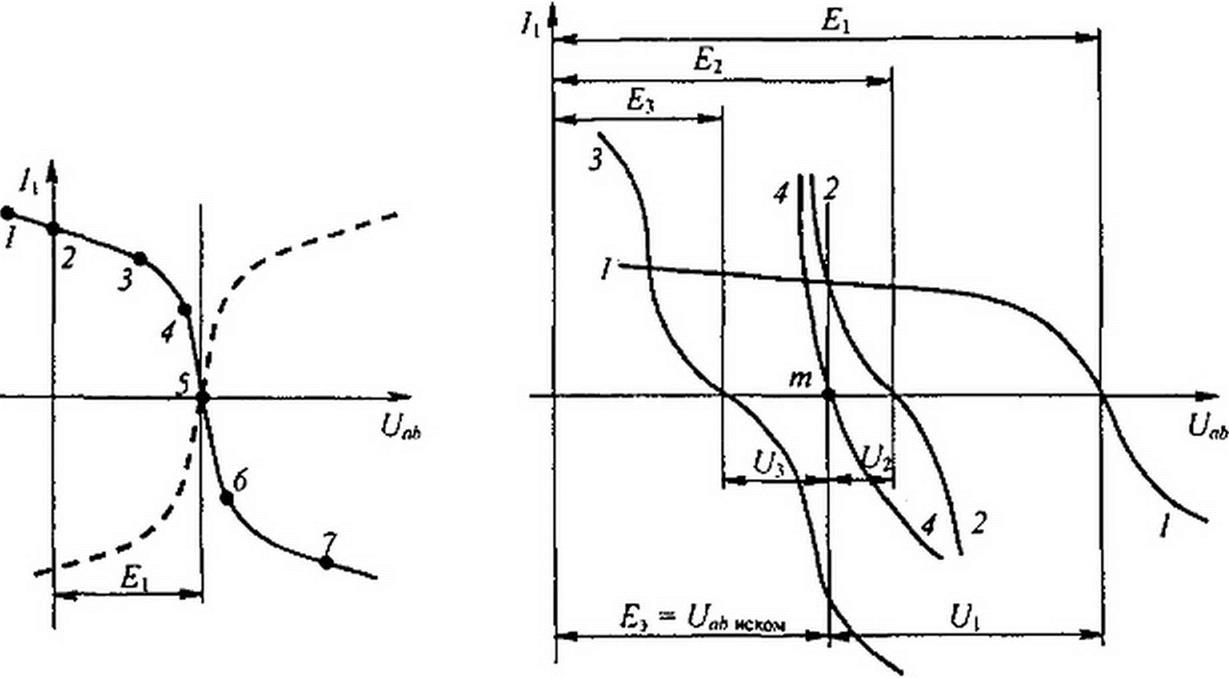
Таким образом, возникает задача о том, как перестроить кривую Л=/(Ц) ^в кривую I\-f(U_ah\ кривую /₂=/({/₂) — ^в кривую /₂ = fWаь) ^{и т}- Д- На рис. 13.8 показано, как из кривой = /(Ц) (рис. 13.7, а) получить кривую - f(U_ab) —точки соответственно обо­значены одинаковыми цифрами.

Для точки 5 кривой (рис. 13.7, а) /, = О и U_} =0; при этом U_ab - Е_} (см. (13.2)), т. е. начало кривой = /{Uah') сдвинуто в точку U_ab ~ £₍.

Росту U_x при Ц >0 соответствует убыль 0_аЬ. Для точки 2 при L/|==£] U_ab=0. Росту £/| при Ц<0 отвечает рост U_ab, причем У_оь>^ ¹ ' ’ '

На основании изложенного рекомендуется поступать следующим об­разом:

§ 1.1 стить кривую /, = /(Ц) параллельно самой себе так, чтобы ее начало находилось в точке U_ab - Е_} (кривая, полученная в результате переноса, представлена штриховой линией на рис. 13.8);

§ 1.2 вести через точку U_ab = Е_} вертикаль и зеркально отразить штриховую линию относительно вертикали.

Аналогичным образом перестраивают кривые и для других ветвей схемы. Нанесем кривые /, = f(U_ab\ /₂ = j\U_ah) ^и Л = f^ab) ^на °Д- ном рисунке (кривые/, 2,3 на рис. 13.9) и построим кривую 7| + /₂ + /3 = f(U_ah) (кривая 4 на рис. 13.9), просуммировав ординаты кривых /, 2, 3. Точка т пересечения кривой 4 с осью абсцисс дает зна­чение U_ah, при котором удовлетворяется уравнение (13.1). Восставим в этой точке перпендикуляр к оси абсцисс. Ординаты точек пересечения перпендикуляра с кривыми /, 2, 3 дадут соответственно токи /,, /₂ и /₃ по величине и по знаку.

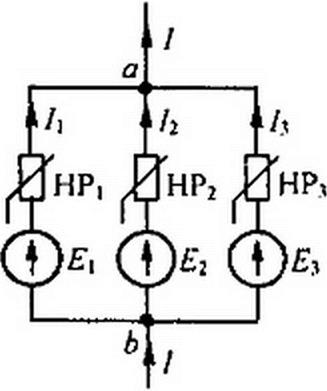
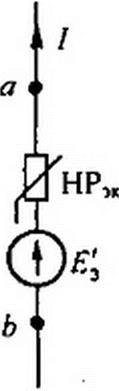
§ 13.8 Замена нескольких параллельных ветвей, содержащих HP и ЭДС, одной эквивалентной. Положим, что имеется совокупность не­скольких параллельных ветвей, содержащих HP и источники ЭДС (рис. 13.10). Параллельные ветви входят в состав сложной схемы, не показанной на рис. 13.10. Каковы должны быть ЭДС и ВАХ эквивалент­ного нелинейного резистора НР_7К участка схемы (рис. 13.11), чтобы он был эквивалентен параллельным ветвям (рис. 13.10)?

Одна ветвь (рис. 13.11) будет эквивалентной ветвям (см. рис. 13.10) в том случае, если ток I в неразветвленной части цепи на рис. 13.10 при любых значениях напряжения U_ab будет равен току I в ветви на рис. 13.11.

Воспользуемся построениями на рис. 13.9. Кривая 4 представляет собой зависимость /, +/₂ +Л ⁼ fWabb ^т- ^е- является результирующей ВАХ трех параллельных ветвей. Такую же ВАХ должна иметь ветвь (рис. 13.11). Если ток I в схеме на рис. 13.11 равен нулю, то U_ab = Е_у Следовательно, Еу на рис. 13.9 определяется напряжением U_ab, при котором кривая 4 пересекает ось абсцисс. Для определения ВАХ НР_ЭК необходимо кривую 4 (см. рис. 13.9) зеркально отразить относительно вертикали, проведенной через точку т.

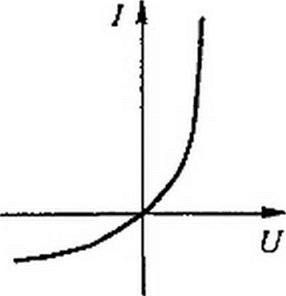
ВАХ НР,_К изображена на рис. 13.12. Важно подчеркнуть, что вклю­чение ЭДС в параллельные ветви привело к тому, что ВАХ НР_ЭК стала несимметричной, несмотря на то что ВАХ нелинейных сопротивлений /, 2, 3 в схеме (см. рис. 13.6) были взяты симметричными.

Таким образом, изменяя ЭДС в ветвях параллельной группы, можно изменять ее результирующую ВАХ и как бы искусственно создавать HP с самыми причудливыми ВАХ.

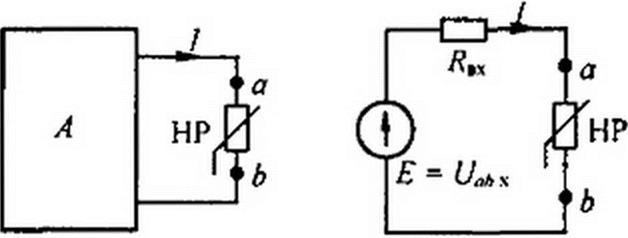
§ 13.9 Расчет нелинейных цепей методом эквивалентного гене­ратора. Если в сложной электрической цепи есть одна ветвь с HP, то оп­ределить ток в ней можно методом эквивалентного генератора. С этой целью выделим ветвь с HP, а всю остальную линейную схему предста­вим в виде активного двухполюсника (рис. 13.13, а).

а б

Рис. 13.13

Как известно из § 2.25, схему линейного активного двухполюсника по отношению к зажимам а и b выделенной ветви можно представить в виде последовательного соединения источника ЭДС с ЭДС, равной напряже­нию на зажимах ab при разомкнутой ветви ab (U_abx\ сопротивления, равного входному сопротивлению /?_вх линейного двухполюсника, и не­линейного сопротивления ветви ab (рис. 13.13,6).

Определение тока в схеме (рис. 13.13, 6) не представляет труда и мо­жет проводиться в соответствии с § 13.4.

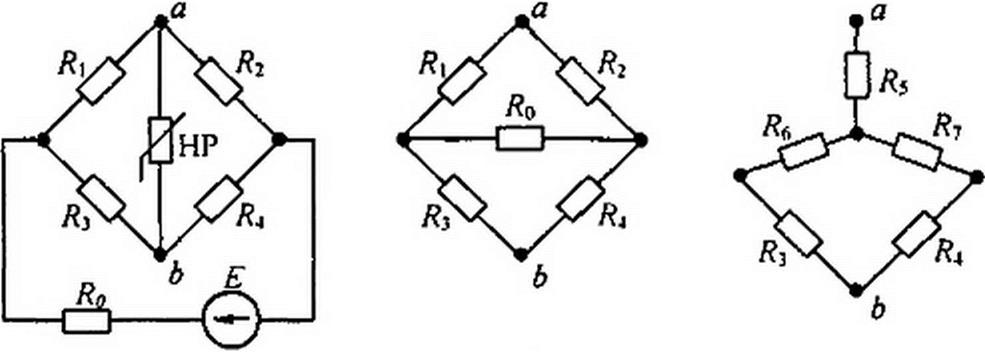
Пример 131. Определить ток в ветви ab схемы (рис. 13.14) по методу эквивалентного генератора при - R_o = 27 Ом; Я₂=Ю8 0м; Я₃=810м; /?₄ = 54 Ом; £ = 70 В. ВАХ HP изображена на рис. 13.15. а.

Решение. Размыкаем ветвь и определяем напряжение холостого хода: U_abx = 20 В.

Для подсчета входного сопротивления Д_ях линейной части схемы относительно за­жимов ab необходимо преобразовать треугольник сопротивлений Я,. Я₂, /?„ (или R₄. Rq, R₃) (рис. 13.14, б) в эквивалентную звезду (рис. 13.14. в) по формулам (2.49-2.51):

, Я| /?*>___________ .

Я₅ = -— — 18 Ом;

/?j + Я₂ ⁺ Л)

Я₆=4,45Ом; Я₇=18 0м;

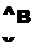
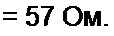_{R ।} (/^ + /?₃)</?₇ +Я₄)
R^ + R₃ + R-j + Я₄

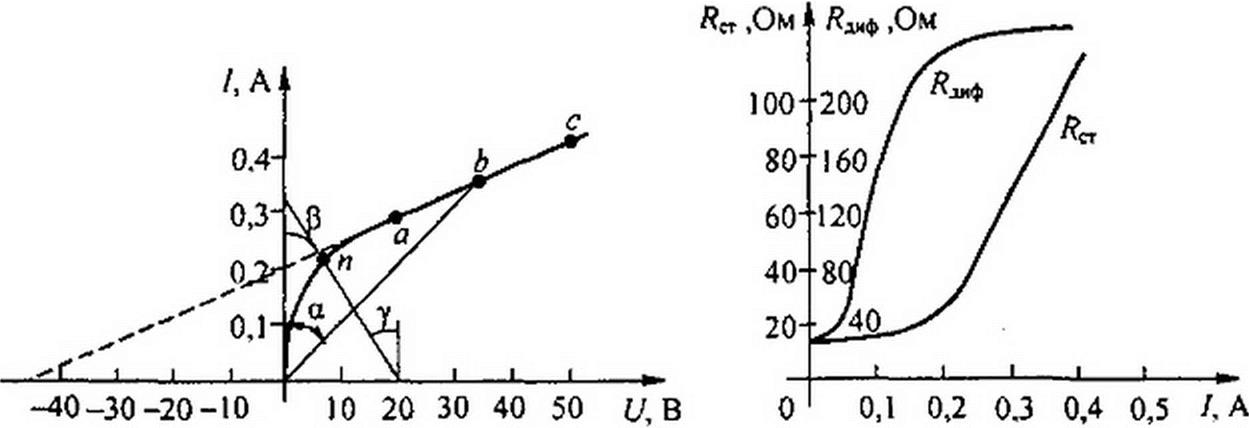
Для определения тока в ветви ab схемы (см. рис. 13.14, а) на рис. 13.15, а проводим прямую, проходящую через точки U ~и„_ь* = 20 В, 1 = 0 и U = 0,

l=U_ahx!R_n =0,351 А

(угол У наклона этой прямой к вертикали с учетом масштабов по осям равен Я_вх ). Точка пересечения этой прямой с ВАХ HP (точка «) определяет рабочий режим схемы. Ток / = 0,22 А.

§ 13.10 Статическое и дифференциальное сопротивления. Свой­ства нелинейного резистора могут быть охарактеризованы либо его ВАХ, либо зависимостями его статического и дифференциального сопротив­лений от тока (напряжения).

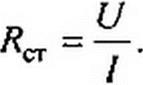Статическое сопротивление R_CJ характеризует поведение HP в режиме неизменного тока. Оно равно отношению напряжения на HP к протекающему по нему току:

(13.5)

Сопротивление /?_ст численно равно тангенсу угла а между осью ординат и прямой, идущей в точку b (рис. 13.15, а), умноженному на от­ношение масштабов по осям т_и I m_t.

При переходе от одной точки ВАХ к соседней статическое сопротив­ление изменяется.

Под дифференциальным сопротивлением /?_лиф принято понимать отношение малого (теоретически бесконечно малого) приращения напря­жения dU на HP к соответствующему приращению тока dl\

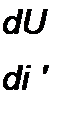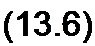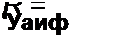Дифференциальное сопротивление численно равно тангенсу угла р (см. рис. 13.15, а) наклона касательной к ВАХ в рабочей точке, умножен­ному на т_(/ / m_t. Оно характеризует поведение HP при достаточно малых отклонениях от предшествующего состояния, т. е. приращение напряже­ния на HP связано с приращением тока, проходящего через него, соот­ношением dU = 2?_ДИф di.

Таким образом, /?_сг — это сопротивление HP по постоянному току, а Я_диф — по малой переменной составляющей.

Если ВАХ HP имеет падающий участок, т. е. такой участок, на котором увеличению напряжения на Д(7, соответствует убыль тока на А/, что имеет место, например, для электрической дуги (см. ее ВАХ на рис. 13.1, д), то дифференциальное сопротивление на этом участке отрицательно.

Из двух сопротивлений (А_ст и /?_диф) чаще применяют Я_диф. Его используют, например, при замене HP эквивалентным линейным сопро­тивлением и источником ЭДС (см. § 13.11), а также при исследовании устойчивости режимов работы нелинейных цепей (см. § 17.3).

Пример 132. Построить кривые зависимости 7?^ и 7?_Д(1ф в функции тока/для нели­нейного сопротивления, ВАХ которого изображена на рис. 13.15, а.

Решение. Кривые построены на рис. 13.15. б.

§ 13.11 Замена нелинейного резистора эквивалентным линейным сопротивлением и ЭДС. Если заранее известно, что изображающая точка будет перемещаться лишь по определенному участку ВАХ HP и этот уча­сток может быть с известной степенью приближения заменен прямой линией, то HP при расчете может быть заменен эквивалентным линей­ным сопротивлением и источником ЭДС.

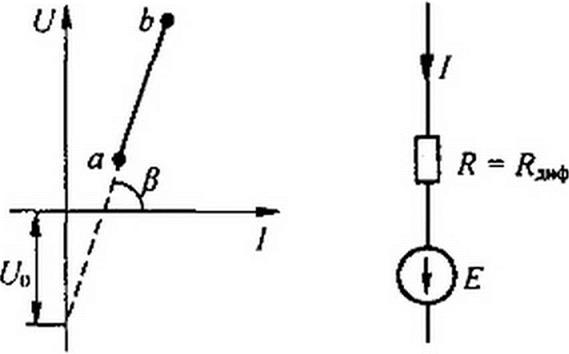
Положим, что рабочая точка перемещается лишь по участку ab (см. рис. 13.15, а и 13.16, а). Для этого участка

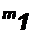(В.7)

Уравнению (13.7) удовлетворяет участок цепи (рис. 13.16, б). На нем Е = -U_Q и линейное сопротивление R = /?_диф.

Замена HP линейным сопротивлением и источников ЭДС удобна тем, что после нее вся схема становится линейной и ее работа может быть исследована методами, разработанными для линейных цепей. Однако при этом необходимо внимательно следить за тем, чтобы рабочая точка не выходила за пределы линейного участка ВАХ.

Пример 133. Выразить аналитически участок ВАХ (см. рис. 13.15, а) в интервале между точками а и с.

Р е ш е н и е. Из рис. 13.15, а находим (У_о = 45 В и Я-шф = 220 Ом. Следовательно, U * -45 + 220 /.

♦ ♦ ♦

Нелинейные резисторы в ряде случаев придают электрическим цепям свойства, принципиально недостижимые в линейных цепях; например, с их помощью можно осуществить стабилизацию тока, стабилизацию на­пряжения, усиление постоянного напряжения и др.

§ 13.12 Стабилизатор тока и стабилизатор напряжения. Стаби­лизаторам тока называют устройство, которое способно поддерживать в нагрузке неизменный ток при изменении сопротивления нагрузки и напряжения на входе всей схемы.

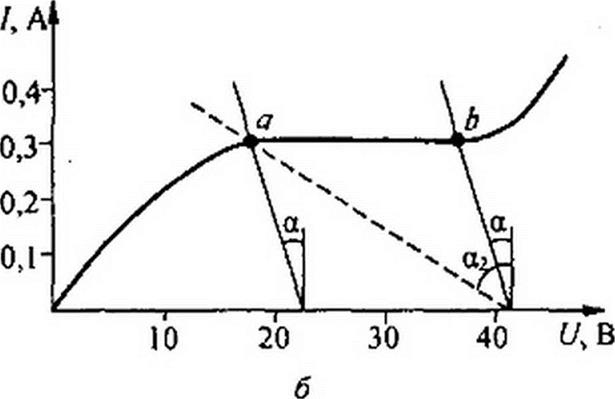
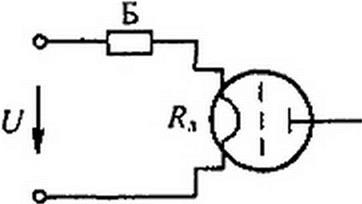
Стабилизацию постоянного тока можно производить с помощью различных схем. Простейшей схемой стабилизатора тока является схема на рис. 13.17, а. В ней последовательно с нагрузкой R„ включен барет­тер Б. На рис. 13.17, б приведена ВАХ бареттера.

Пример 134. Бареттер используют для стабилизации тока накала электронной лампы. Номинальный ток накала 0.3 А, напряжение 6 В. Определить, в каких пределах можно

изменять напряжение 1) на входе схемы, чтобы ток нити накала лампы оставался неиз­менным и равным 0,3 А.

Решение. Сопротивление нити накала лампы R_n = 6/0,3 = 20 Ом.

Проводим через точки а и Ь (рис. 13.17, б), ограничивающие участок баретгирования, две прямые под углом a (iga с учетом масштабов по осям численно равен 20) к вертикали. По рис. 13.17, б определяем, что напряжение U можно изменять в интервале 22-41 В.

Пример 13S. В схему предыдущей задачи введено последовательное сопротивле­ние /?]. Полагая напряжение на входе схемы неизменным и равным 41 В, найти, до како­го максимального значения R_f в схеме имеет место стабилизация тока.

Решение. Если /?|=0 и (7-41 В. то рабочий режим характеризуется положени­ем точки b (см. рис. 13.17, б). С увеличением сопротивления рабочая точка на ВАХ перемещается по направлению к точке а. В граничном режиме (точка а}

^Imax ⁺ ~ ^! S ^а 2 —~ ⁼

Следовательно, /?_)тдх = 80 - 20 = 60 Ом.

Стабилизатором напряжения называют устройство, напряжение на выходе которого 1/_и поддерживается постоянным или почти постоянным при изменении сопротивления нагрузки /?_н или напряжения Ц на вхо­де устройства.

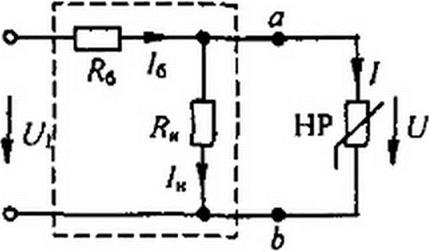
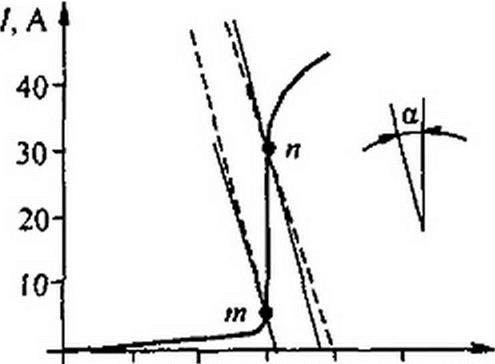
Схема простейшего стабилизатора напряжения приведена на рис. 13.18. В качестве HP используется стабилитрон; — балластное сопротивление. На рис. 13.19 изображена ВАХ стабилитрона.

При анализе работы стабилизатора определяют пределы допустимых изменений при /?_н = const, а также исследуют работу стабилизатора при одновременном изменении /7₍ и /?_н.

Для оценки качества работы стабилизатора иногда пользуются поня­тием коэффициента стабилизации. Под ним понимают отношение от­носительного приращения напряжения на входе стабилизатора (A(/_t к относительному приращению напряжения на выходе стабилизатора

Пример 136. В схеме на рис. 13.18 R_H ~ 5 кОм; = 2 кОм. ВАХ стабилитрона со­ответствует рис. 13.19. Определить границы допустимого изменения {/,. при которых на выходе стабилитрона поддерживается стабилизированное напряжение 150 В.

Решение. Воспользуемся методом эквивалентного генератора. Разомкнем ветвь ста­билитрона и найдем напряжение холостого хода;

U„_b. = и. ^R " = 0,713 и.: /!„„,= = 1427 Ом.

На рис. 13.19 проведем две прямые (сплошные) линии через точки тип ВАХ стаби­литрона так, чтобы тангенс угла (образованного ими с вертикалью), умноженный на т_и!т_!у был равен = 1427О.М.

Отрезки, отсекаемые этими прямыми на оси абсцисс, равны U_aflK. Из рис. 13.19 на­ходим 0,713(/_1гпщ = 220 В, или l/_Imin = 220 В. Аналогично 0,713 t/_lmax = 192 В, или

⁼ 269 В. Следовательно, напряжение может изменяться от 220 до 269 В.

Пример 137. Для схемы на рис. 13.18 при /?₅ = 2,5 кОм (ВАХ стабилитрона см. на рис. 13.19) и О] = 250 В определить, в каких пределах можно изменять сопротивление на­грузки /?_н, чтобы стабилизатор мог выполнять свои функции по стабилизации выходного напряжения.

Решение. Составим уравнение по второму закону Кирхгофа: R₆ + U = U\. Под­ставив в него

^/6 ^{= /}4 ^{+ /i}y^+/- получим

U (1 + /?□//?„)+ / R₅=U_}. (13.8)

Из (13.8) следует, что при (J = 0 / = (/,/ /?₅ = 250/2000 = 125 мА.

Отметим положение этой точки на оси ординат (рис. 13.19) и штриховой линией про­ведем из нее два луча, чтобы они проходили через точки т и п, ограничивающие участок стабилизации. Решим уравнение (13.8) относительно :

и

_{R =}---------------------------- (13.9)

((7,-0)/^-/

Уравнение (13.9) применим дважды: один раз. используя координаты точки т, другой раз — точки п. Для точки т / = 5мА; U = 150 В; и Я_н) = 4.28 кОм. Для точки п / = 30 мА; U - 157 В; /?_н2 = 9,52 кОм. Таким образом, сопротивление можно изменять от 4,28 до 9,52 кОм.

Пример 138. В схеме на рис. 13.20. а к источнику ЭДС Е присоединены туннельный диод (его ВАХ — кривая на рис. 13.20, б) и линейный резистор R.

Построить зависимость; 1) тока / от изменения R при Е - 0,5 В; 2) тока / от ЭДС Е при Я = Ю0Ом.

Решение. Построение для случая I дано на рис. 13.20. в и для случая 2 — на рис. 13.20, г. Кривые построены по точкам пересечения ВАХ диода (кривой а

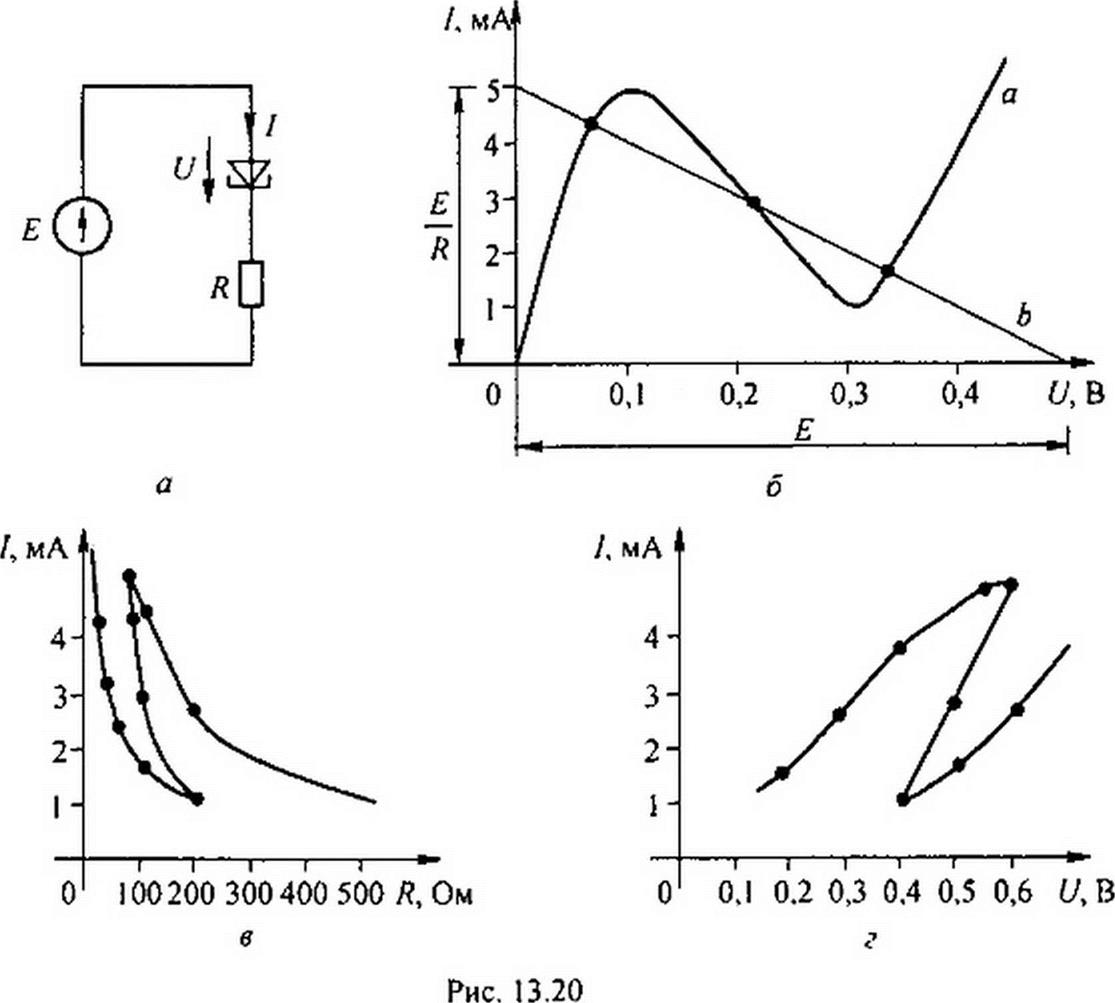рис. 13.20.5) с ВАХ резистора R (прямая Ь, ее координаты U = 0, / = Е/ R, и U = Е, 7 - 0). В случае 1 проводим несколько прямых при различных R. в случае 2 прямую b переносим параллельно самой себе.

§ 13.13 Применение теории линейного активного автономного четырехполюсни­ка к расчету нелинейных цепей. На рис. 13.21, а штриховой линией обведен линейный активный автономный четырехполюсник, в двух удаленных друг от друга ветвях 7 и 2 которых имеются нелинейные резисторы НЭ| и НЭ₂. вольт-амперные характеристики которых известны. Требуется определить токи /| и /₂ в ветвях 7 и 2.

С этой целью в соответствии с § 4.5 и 4.16 линейную часть схемы на рис. 13.21, а заменим линейной активной Т-схемой замещения (рис. 13.21,5). Она состоит из трех резисторов— /?|, /?,. Я- и двух источников постоянной ЭДС—Е\ и Е_г. Чтобы опре­делить параметры схемы на рис. 13.21, 5, поступим следующим образом.

1. В схеме на рис. 13.21, а разомкнем ветви 1 и 2, содержащие НЭ, и образовавшую­ся после этой процедуры линейную часть схемы сделаем пассивной, мысленно разомкнув в образовавшейся схеме ветви с источниками тока и закоротив ветви с источниками ЭДС.

2. Затем определим три входных сопротивления для образовавшейся пассивной схе­мы на рис. 13.21, в: входное сопротивление Л, _х по отношению к зажимам /—7 при ра­зомкнутой второй ветви, входное сопротивление Я_1к по отношению к зажимам 7—/ при коротком замыкании второй ветви и входное сопротивление Я_2х по отношению к зажи­мам 2—2 при разомкнутой первой ветви.

3. Располагая значениями Я_1Х, Я_)х, Я_2х по формулам (4.32) определим А, В, С, D параметры пассивного четырехполюсника:

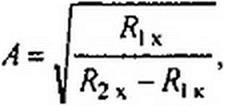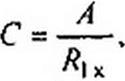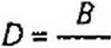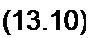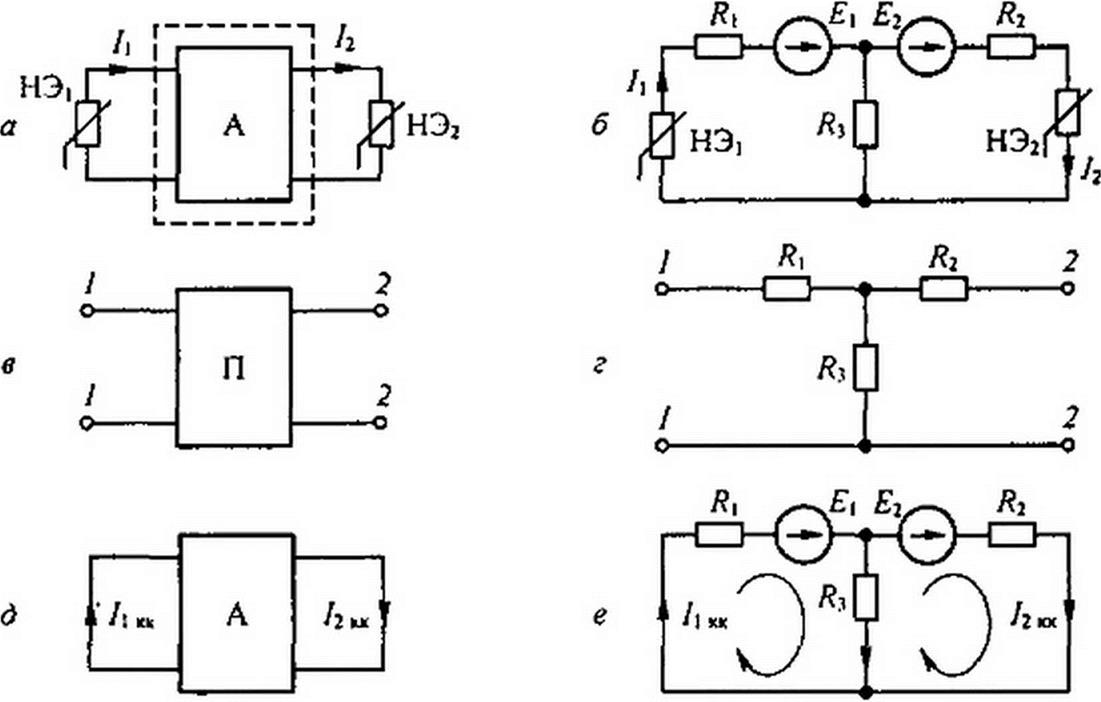
Рис. 13.21

4. По А, В, С_у D параметрам определим сопротивления . /?₂, эквивалентной пассивной схемы на рис. 13.21, г:

R2=~-. л, = 1 (13.П)

5. Для определения ЭДС £, и £₂ в схеме на рис. 13.21. б осуществим короткое замыкание в ветвях / и 2 (см. рис. д и е) и расчетным путем определим токи l_iKK и /_2хк в схеме на рис. 13.21, д, которые равны токам в схеме на рис. 13.21, е. Для схемы на рис. 13.21 ,е составим два уравнения:

Л хк ⁺ (Л кк “ ^2 хк ) ^3 ~ £| (13.1 2)

^2кк ^2 “(Лхх ^_^2кх) ^3 = ^2 (13.13)

и из них определим Е_х и £₂. Расчет токов в схеме на рис. 13.23, б рассмотрен в § 13.7.

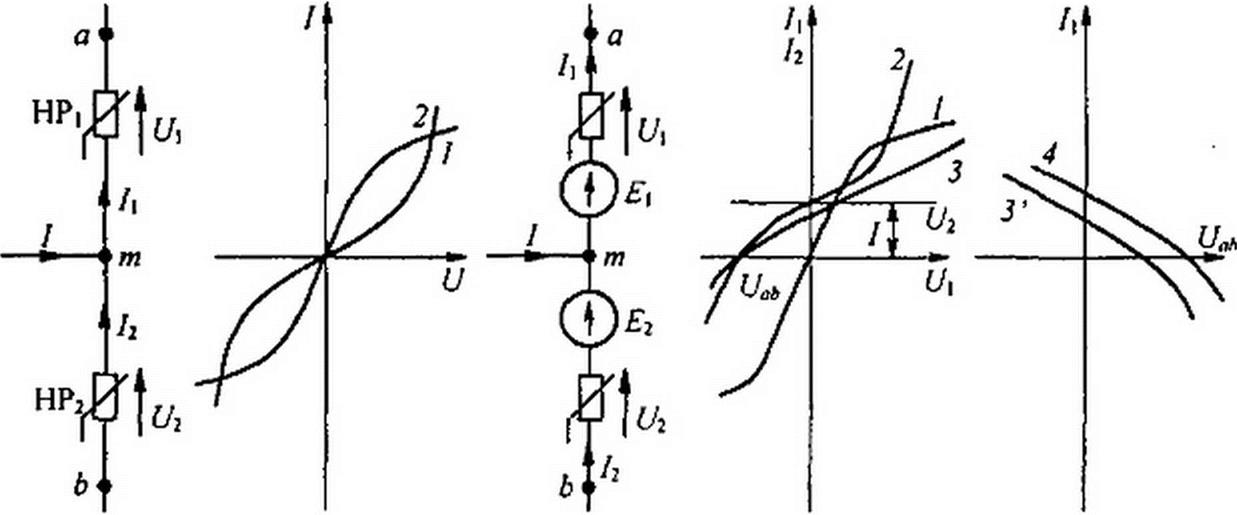
6. 13.14. Построение ВАХ участков цепей, содержащих узлы с подтекающими из* вне токами. На рис. 13.22, а изображен участок цепи, между точками а и Ь которого име­ются НР| и НР₂, а к узлу т подтекает ток 1 от нспоказанной на рисунке части схемы. ВАХ НР₂ и НР₂ известны (рис. 13.22, б). Требуется построить семейство ВАХ Л = при нескольких фиксированных значениях тока 7. При любом U_ah ток Ц боль­ше тока /₂ на ток I. Это учтено при построениях на рис. 13.22, г тем, что начало кривой 7₂ = /(0'₂) смещено выше начала кривой 1_Х = j\V_x} на ток 7. Из рис. 13.22, а следует, что U_ba~U_x+ U₂ или U_ab - + U₂ )■

Для построения кривой при / = const задаемся произвольным током /_t,

проводим через это значение 7, горизонталь и суммируем абсциссы пересечения этой горизонтали с абсциссами кривых / и 2. Получаем кривую 5. Кривая 7₍ = f(.U_ab) (кри­вая З¹) на рис. 13.22,6 получается из кривой 3 (рис. 13.22,г) зеркальным отражением относительно вертикальной оси. При ином значении 1 будет новая кривая 7_t ~ Если на участках 7 и 2 будут включены ЭДС £₍ и £₂ (рис. 13.22, в), то С7„_А = -(^+У₂)+£₁+£₂.

ВАХ 7] = в этом случае получаем параллельным переносом кривой 3

(рис. 13.22, 6) на (£_t +£₂) — кривая 4.

а и в г д

Рис. 13.22

7. 13.15. Диакоптика нелинейных цепей постоянного тока. Под диакоптикой по­нимают расчет сложных цепей по частям, с учетом влияния частей друг на друга.

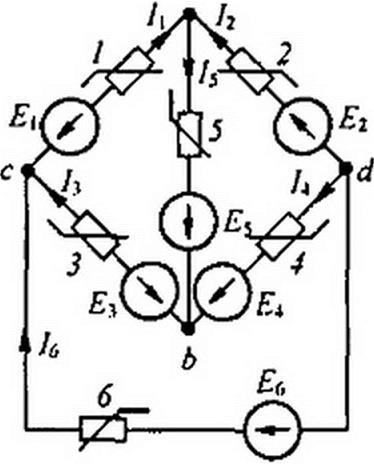
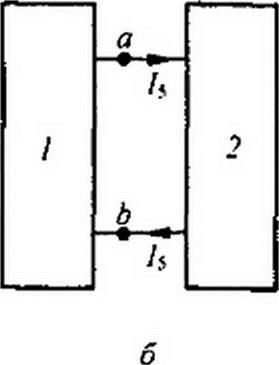
Проиллюстрируем идею метода на примере схемы (рис. 13.23, а). Это мостовая схема с шестью ветвями и шестью HP. Всю схему, за исключением ветви 5 с током /$, предста­вим на рис. 13.23, б некоторым нелинейным двухполюсником I, а ветвь 5 — двухполюс­ником 2. Общим для них является ветвь ab с током /₅.

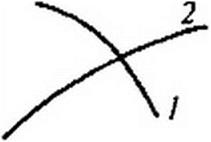Если на рис. 13.23, в построить кривую /5 = — кривую / — для двухполюс­ника / и кривую /5 = — кривую 2 — для двухполюсника 2, то точка пересечения

кривых / и 2 удовлетворяет работе обеих частей схемы, т. е. является решением задачи.

Для получения кривой I необходимо в соответствий с § 13.14 сначала построить семейство ВАХ ветвей / и 2 /₍ - и ВАХ ветвей 3 и 4 /₃ = при различных /5. Затем учесть, что /_} + /₃ + /₆ = 0 для каждого Л- Из этого условия определить U_cd, /р 1у для каждого фиксированного /5 и по ним построить /5 = j\U_Ob\

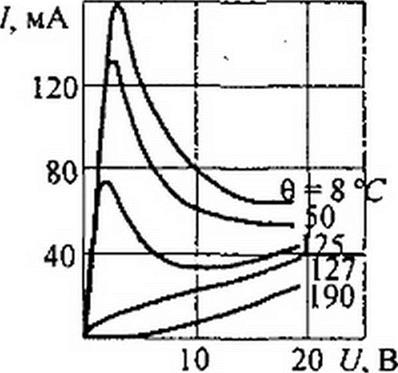
8. 13.16. Терморезнсторы. Терморезисторы представляют собой HP, сопротивление которых сильно зависит от температуры Т тела терморезистора. Так как эта температура зависит не только от тока, проходящего по терморезистору, но и от температуры окружаю­щей среды 0, то они представляют собой температурно управляемые HP. Другими слова­ми, один и тот же терморезистор обладает различными ВАХ при различных 0. Ток,
нагревающий терморезистор, может проходить по самому тсрморезистору либо по нагре­вательной обмотке, электрически изолированной от него.

Терморезисторы подразделяют на два класса: термисторы (с отрицательным темпера­турным коэффициентом) и позисторы (с положительным температурным коэффициентом). Термисторы изготовляют из оксидов меди и марганца, позисторы — из титаната бария, легированного редкоземельными металлами. Постоянная времени нагрева терморезисто­ров составляет обычно несколько десятков секунд. Обозначают терморезисторы в соот­ветствии с рис. 13.24, а, ставя соответственно букву Т или П.

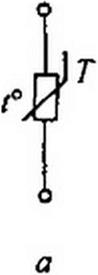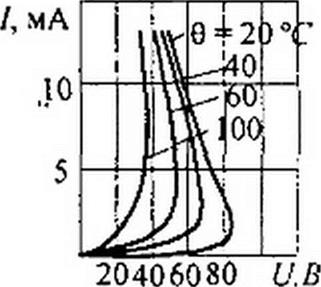
На рис. 13.24. б изображены ВАХ термистора типа ММТ-4. а на рис. 13.24, в — по­зистора CT5-I.

9. 13.17. Фоторезистор и фотодиод. Фоторезистор — это резистор, управляемый световым потоком Ф. Действие его основано на внутреннем фотоэффекте. ВАХ при неиз­менном потоке показана на рис. 13.25. а, люкс-амперная'¹ характеристика при неизменном напряжении — на рис. 13.25, б, спектральная характеристика I - /(X) (ток — в относи­тельных единицах, X — длина волны) при неизменном U и Ф — на рис. 13.25, в. частот­ная характеристика <р(/) при неизменном Ф и U — на рис. 13.25, г.

а б в г

Рис. 13.25

Фотодиод (ФД) — это германиевый или кремниевый диод, обратный ток р-п-персхо- да которого зависит от освещенности перехода. Работа его основана на вентильном фото­эффекте.

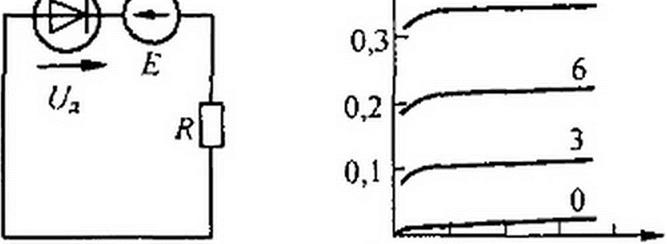
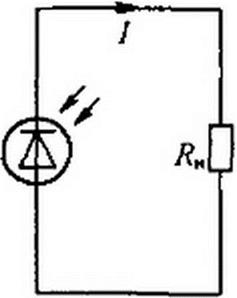
ФД могут работать с внешним источником (схема на рис. 13.26, а) и без него (рис. 13.27, а). ВАХ одного из типов серно-таллиевого ФД при различных Ф изображена на рис. 13.26, б.

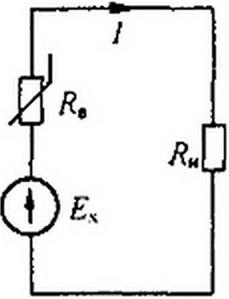
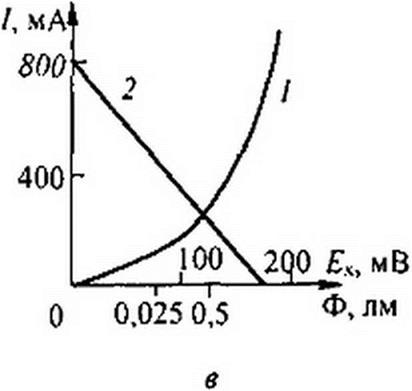
При работе без внешнего источника питания фотогальваническая ЭДС достигает 0,1-0,2 В и более. Схема замещения для рис. 13.27, а изображена на рис. 13.27,6. ФД на нем представлен источником ЭДС холостого хода Е_х и внутренним сопротивлени­ем ЭДС Е_х — нелинейная функция светового потока Ф. ВАХ — кривая / на

*’ Люкс — это люмен / м^: — единица измерения освещенности.

а б

Рис. 13.26

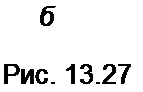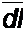
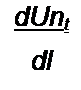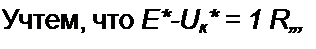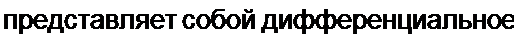рис. 13.27, в, а прямая 2— ВАХ Я_н при Е_п -0,28 и Я* = 250 Ом. Пересечение J с 2 определяет рабочий режим.

§ 13.18 Передача максимальной мощности линейной нагрузке от источника с нелинейным внутренним сопротивлением. В схеме на рис. 13.27, б линейной нагрузке сопротивлением R* передается мощность от источника ЭДС через резистор R_t, имеющий нелинейную ВАХ (кривая 1 на рис. 13.27, а). Обозначим через U— напряжение на не­линейном резисторе. Мощность, выделяющаяся в нагрузке.

Р„=! R„I = {E,-U^1.

о ^dP»

Возьмем производную ---------- и приравняем ее нулю:

d I

dU_K
к -I—^- = 0.

dl

сопротивление нелинейного резистора. Следовательно, максимальная мощность передается нагрузке, когда в рабочей точке Я_и = Я_Л11ф-

Если в схеме на рис. 13.27, б нелинейным будет не только внутреннее сопротивление источника питания, но и сопротивление нагрузки, то нагрузке будет передаваться макси­мальная мощность (энергия), когда в рабочей точке статическое сопротивление нагрузки равно дифференциальному сопротивлению источника питания (доказывается аналогично).

§ 13.19 Магниторезисторы и магнитодиоды. Магниторезисторы — это резисто­ры. сопротивлением которых управляют внешним магнитным полем индукции В, направ­ленным перпендикулярно направлению протекания тока через резистор. Электроны в теле магниторезистора находятся в перекрестных магнитном поле индукции В и электриче-

а б в

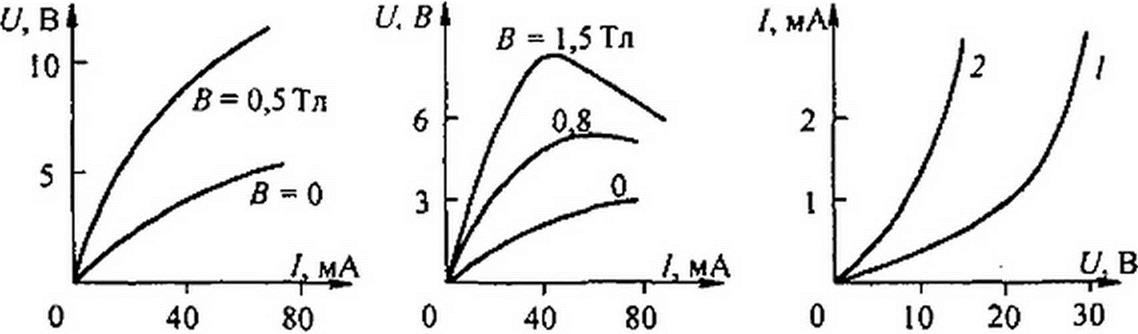
Рис. 13.28

ском поле напряженностью Ё и движутся не по напряженности поля Ё, а по кривой, напоминающей циклоиду, за счет чего путь их, а следовательно, и сопротивление увели* чиваются. Выполняют их в виде дисков или пленок. На рис. 13.28, а изображена ВАХ магниторезистора из антимонида индия, а на рис. 13.28, б — из арсенида индия.

Магнитодиоды — это диоды, в которых магнитное поле изменяет подвижность и на­правление движения электронов и дырок. На рис. 13.28, в изображена ВАХ магнитодиода КД301Ж при 5 = 0 (кривая I) и при 5 = 0,ЗТя (кривая 2).

Вопросы для самопроверки

1. Дайте определения следующим понятиям: нелинейный резистор, нелинейная элек­трическая цепь, статическое и дифференциальное сопротивления. 2. Дайте определение неуправляемых HP. 3. Качественно изобразите ВАХ известных вам типов неуправляемых и управляемых HP. 4. Для каких известных вам типов HP дифференциальное сопротивле­ние может быть отрицательным? 5. Может ли для реальных HP статическое сопротивле­ние быть отрицательным? 6. В чем заключается препятствие, затрудняющее применять метод контурных токов или метод узловых потенциалов для расчета сложных разветвлен­ных нелинейных цепей? 7. Как заменить несколько параллельных ветвей с HP и источни­ками ЭДС на одну эквивалентную? Определите характеристики элементов эквивалентной ветви. 8, Перечислите этапы расчета нелинейных целей (НЦ) методом двух узлов и мето­дом эквивалентного генератора. 9. В чем ограниченность метода замены HP эквивалент­ным линейным сопротивлением и источником ЭДС? 10. Перечислите свойства, которыми при определенных условиях могут обладать НЦ и не обладают линейные цепи. И. Оха­рактеризуйте свойства термисторов и позисторов, фото- и магниторезисторов. 12. Пояс­ните идею расчета схем с применением диакоптики. 13. В чем отличие условий передачи активной мощности нагрузке от источника с нелинейным внутренним сопротивлением и от источника с линейным сопротивлением? 14. Решите задачи 2.4, 2.8, 2.13, 2.14, 2.15, 2.20, 2.22.

Глава четырнадцатая

МАГНИТНЫЕ ЦЕПИ

§ 14.1 Подразделение веществ на сильномагнитные и слабомаг­нитные. Из курса физики известно, что все вещества по их магнитным свойствам подразделяют на диамагнитные, парамагнитные, ферромагнит­ные, ферримагнитные и антиферромагнитные. У диамагнитных веществ относительная магнитная проницаемость р_г <1, например для висмута р, = 0,99983, у парамагнитных веществ > I, например для платины

= 1,00036. У ферромагнитных веществ (железо, кобальт и их сплавы) много больше единицы (например, 10⁴, а У некоторых материалов даже до Ю⁶). У ферримагнитных веществ р_г того же порядка, что и у ферромагнитных, а у антиферромагнитных веществ того же поряд­ка, что и у парамагнитных.

При решении большинства электротехнических задач достаточно подразделять все вещества не на перечисленные группы, а на сильномаг­нитные, у которых » 1, и на слабомагнитные (практически немагнит­ные), у которых р_г

§ 14.2 Основные величины, характеризующие магнитное поле. Основными векторными величинами, характеризующими магнитное поле, являются магнитная индукция В и намагниченность J*\