Четвертая стадия процесса заключается в том, что на три предыдущие волны накладывается четвертая волна, представляющая собой отражение от разомкнутого конца линии второй падающей волны.
Отражение второй падающей волны от конца линии произойдет в соответствии со схемой замещения рис. 12.4, о, только вместо 2 мп1 = 2 и в схеме будет напряжение 2 мп2 = -2 и.
Вторая отраженная волна имеет ио2 = -и, io2 = i- Результирующее состояние на линии во время четвертой стадии (рис. 12.3, г) есть результат наложения четырех волн:
«п| + «»| + «п2 + "о2 = “ + “ - “ - “ = °;
'nl+'ol+'n2+'o!='-'-' + ' = °.
Таким образом, к концу четвертой стадии напряжение и ток вдоль всей линии равны нулю — линия приобретает такое же состояние, какое у нее было к началу первой стадии. Затем процесс повторяется до бесконечно, так как Rq и Go были приняты равными нулю. В действительности благодаря наличию сопротивления и утечки GQ колебательный процесс постепенно затухает и вдоль линии устанавливается режим, соответствующий установившемуся процессу в линии при постоянном напряжении.
В рассмотренном примере линия на конце была разомкнута, поэтому отраженные волны имели такую же прямоугольную форму, как и падающие.
Отраженные волны будут иметь форму, в общем случае не похожую на форму падающей волны, если в состав нагрузки на конце линии входят емкости и (или) индуктивности, а также в том случае, если в месте перехода с одной линии на другую есть сосредоточенные индуктивности и (или) емкости.
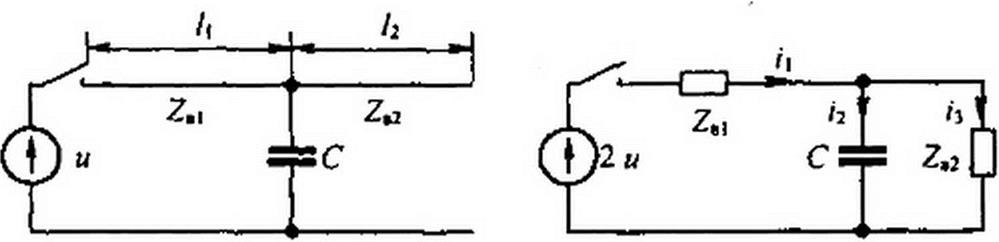
§ 12,8. Переходный процесс при подключении источника постоянного напряжения к двум последовательно соединенным линиям прн наличии емкости в месте стыка линий. Пусть первая линия имеет длину /, и волновое сопротивление ZB1, вторая линия — длину /2 и Zb2 *ZB>. Напряжение источника ЭДС равно и (рис. 12.5, а). В месте стыка линий есть сосредоточенная емкость С.
а б
Рис. 12.5
Требуется определить форму волны, проникающей во вторую линию, характер изменения тока через сосредоточенную емкость, а также результирующее распределение напряжения и тока вдоль первой линии при движении по ней отраженной от стыка линий волны.
Переходный процесс начинается с того, что от генератора по первой линии распространяется падающая волна с прямоугольным фронтом "п! =* И 41 =
Для определения характера изменения токов и напряжений, когда падающая волна дойдет до стыка линий, обратимся к схеме замещения с сосредоточенными параметрами рис. 12.5, б. В этой схеме нагрузка образована двумя параллельными ветвями — емкостью С и волновым сопротивлением второй линии Zb2.
Две параллельные ветви появились в схеме замещения потому, что в исходной схеме рис. 12.5, а падающая волна, дойдя до места стыка линий, встречает два пути для своего дальнейшего распространения: первый путь — через емкость С, второй путь — по второй линии с волновым сопротивлением Zb2.
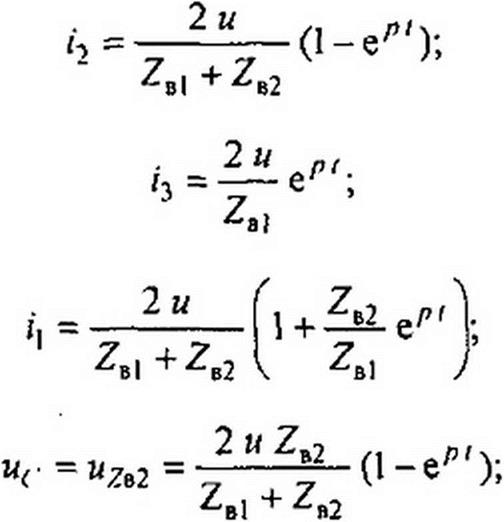
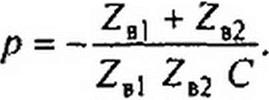 Расчет переходного процесса в схеме рис. 12.5, б дает:
Расчет переходного процесса в схеме рис. 12.5, б дает:
(12.31)
(12.32)
(12.33)
(12.34) (12.35)
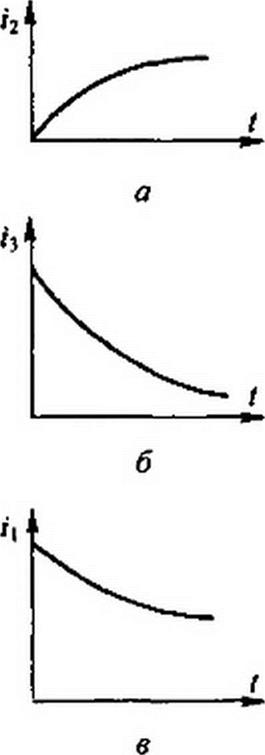
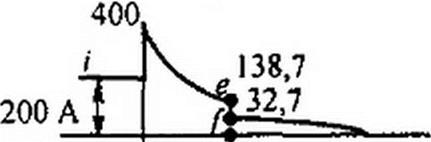
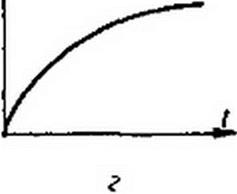
Характер изменения /2, /3, /{ и и( в функции от времени изображен на рис. 12.6, а-г. В первый момент после подхода волны к месту стыка линий напряжение падает до нуля, так как незаряженный конденсатор для этого момента времени представляет собой как бы короткое замыкание.
Начальное значение тока через конденсатор равно 2u/ZB). Затем конденсатор заряжается, напряжение на нем растет, а ток через него уменьшается. Ток ь в схеме замещения представляет собой ток электромагнитной волны, распространяющейся по второй линии; напряжение волны, распространяющейся по второй линии, равно /2 Zb2.
Для получения отраженной волны напряжения, распространяющейся по первой линии в направлении от стыка линий к генератору, из ординат кривой рис. 12.6, г нужно вычесть соответствующие ординаты напряже-
 | ||||
 | ||||
 | ||||
|
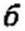 | |||||
 | |||||
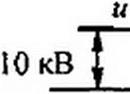 | |||||
 | |||
| |||
 |
| ||||
| ||||
 |
|
 |
|
 |
ния падающей волны и затем перенести полученную кривую на линию, зная скорость отраженной волны.
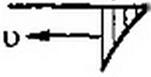
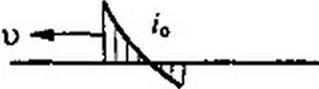
На рис. 12.7, а, б изображены, соответственно, отраженные волны напряжения и тока.
Эпюра распределения напряжения и тока вдоль первой и второй линий для момента времени, когда отраженная от стыка волна дошла до середины первой линии, представлена, соответственно, на рис. 12.7, в, г.
Перепад тока ef в кривой рис. 12.7, г равен току через конденсатор для данного момента времени. По второй линии волна продвинулась на расстояние, вдвое большее, чем прошла отраженная волна по первой линии. Это объясняется тем, что первая линия — кабельная, а вторая — воздушная. Скорость продвижения волны по воздушной линии — 300 000 км/с, а по кабельной — около 150 000 км/с (формула для скорости и движения волны по линии и входящие в нее Ао и Со приведены в § 11.10).
Пример 130. В схеме на рис. 12.5, a Ze] = 50 Ом; Zb2 =400 0m; ^=100 км; С ~ 5,62 мкФ; /] = 60 км; и = 10 кВ. Первая линия — кабельная, вторая — воздушная. Построить эпюры распределения волн напряжения и тока вдоль линий для момента времени, когда распространяющаяся по второй линии волна дойдет до конца второй линии.
Реш е ние. По формуле (12.35) р =--------------------- 50 + 400-------------------------------------------------------------------- -4000 с-1.
50-400-5,62-10"6
Ток падающей волны по первой линии /п =«/Ze1 = Ю4/50-200 А.
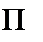 | 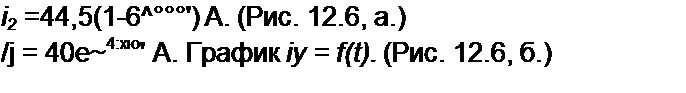 | ||||||||
 | |||||||||
 | |||||||||
 | |||||||||
По формуле (12.33), /2 = 44,5(1 +8 е“4000/) А. (Рис. 12.6, в.)
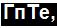
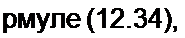 = «2.2 = 17750(1-е’4000') В. (Рис. 12.6, г.)
= «2.2 = 17750(1-е’4000') В. (Рис. 12.6, г.)
По условию, падающая по второй (воздушной) линии волна должна дойти до конца второй линии. Расстояние /2 = 100 км она пройдет за время
t = 12 /и = 100/300000 = 1/3000 с.
За это время отраженная от стыка волна пройдет по первой кабельной линии расстояние, в два раза меньшее.
Графики распределения и и / вдоль линии изображены на рис. 12.7, а, б.
Перепад ef на рис. 12.7, б равен току /3 при / = 1/ЗОООс; м = 400е-4/3 = 106 А.
Отрезок gf равен току i2 при / = 1/3000с; = 44,5(1-e"4/j = 32,7 А,
Отрезок мп на рис. 12.7, а равен напряжению ис при t = 1/3000с; и(-= 13,05 кВ.
В рассмотренном примере электрическая цепь, содержащая линию с распределенными параметрами, подключалась к источнику постоянного напряжения.
Однако часто встречаются цепи, в которых ЭДС источника изменяется по синусоидальному закону во времени. Если длина линии с распределенными параметрами и частота синусоидальной ЭДС таковы, что время пробега волны по линии (/ = / /и) много меньше периода перемен- ( 1
него тока Г, например составляет величину порядка I — =• — 11, то при исследовании первых стадий переходного процесса в первом грубом приближении можно принять, что линия подключается к источнику постоянной ЭДС, которая равна амплитуде синусоидальной ЭДС (расчет на наиболее тяжелый случай). Если же время пробега волны по линии со-
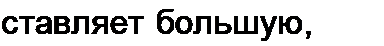 — -г — L часть периода, то при расчетах учи
— -г — L часть периода, то при расчетах учи
тывают изменение ЭДС источника при перемещении падающей волны по линии.
При отключении нагрузки или ее части в линиях также возникают переходные процессы. Расчет их производят на основании принципа наложения, включая в размыкаемую ветвь источник тока, который дает ток, равный и противоположно направленный току в размыкаемой ветви.
Результирующие волны тока и напряжения на всех участках линии находят наложением на волны тока и напряжения, которые были на линии до отключения ветви, волн тока и напряжения, продвигающихся от места размыкания в остальные участки линии.
При подключении в каком-либо месте линии новой ветви токи и напряжения в этой ветви находят методом эквивалентного генератора, а токи в остальных участках линии — методом наложения.
§ 12.9. Линия задержки. Подлинней задержки, применяемой в импульсной технике, понимают устройство, которое включают между источником сигнала и нагрузкой, служащее для задержки поступления сигнала в нагрузку на некоторое заданное время /3. В простейшем случае
(при малом t3) линию задержки выполняют в виде куска коаксиального кабеля длиной /. Он создает задержку h =//иф. Если хотят получить относительно большое г3, то используют цепочку из каскадно соединенных одинаковых фильтров низкой частоты (см. рис. 5.1, а)у выбирая параметры L и С фильтров так, чтобы полоса частот сигнала Оч-сос находилась 1*__полосе прозрачности фильтра и чтобы а)с<©2> где со 2 =у/2 /LC — частота среза фильтра. Параметры фильтра согласуют с нагрузкой RH - ^2 L/C. Время задержки Г3 ~ п (db/с/св)ш=0 = п у/2 L С. Содержание, вкладываемое в термин «время задержки» (ВЗ) линии и четырехполюсника, различно. ВЗ линии — это время прохождения линии электромагнитной волной. ВЗ, оказываемое четырехполюсником, — это время, отсчитываемое от момента поступления сигнала на вход четырехполюсника до момента, когда напряжение на выходе его нарастает от нуля до некоторого определенного значения, скажем до 0,5 от амплитудного, при относительно небольшом изменении формы сигнала по сравнению с входным. Физически это время обусловлено переходным процессом в самом четырехполюснике и нагрузке. Выведем записанную формулу для /3.
В § 9.5 было показано, что передаточная функция четырехполюсника /0 = 1\ во времени, должна обладать двумя свойствами:
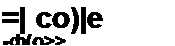 | |||||
 | |||||
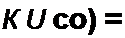 | |||||
1) модуль i K( j ю)|= const (в частности, равен единице);
2) аргумент $0 to) = -со .
Применительно к фильтру K(j со) - 1/е* = l/(efle'A). Сопоставление характеристик фильтра с характеристиками четырехполюсника для зоны прозрачности дает
|К(усо)|=1/ев =1, А = -Ф(<о) = со/;.
Для фильтра НЧ (см. рис. 5.1, а) в зоне прозрачности b = arccos А = arccos(l - со2 £ С)
нелинейно зависит от со. Для определения времени задержки приближенно заменим эту нелинейную зависимость прямой с угловым коэффициентом, равным | , т. е. ло-
ложим b = со --------
Тогда время задержки, создаваемое одним фильтром,
- = (- db Ю =
G 'l>Lo ~ rf(l-co2 LC} da
—............................ (-2 со L С) *-------- -L— (-2 со L С) = у/2 LC.
Vl-(l-co2 LC)2 a-J2LC
Если каскадно соединены л фильтров НЧ, то время задержки в п раз больше: = п у/2 L C.
Если сигнал, проходящий через четырехполюсник, представляет собой короткий импульс, то его частотный спектр весьма широк и четырехполюсник, в отличие от линии с распределенными параметрами, нс в состоянии пропустить без затухания колебания всех частот. В этом случае можно только условно говорить о времени задержки, понимая под ним ус- db '
редненную производную —, подсчитанную для основной части частотного спектра. da
§ 12.10 Использование линий для формирования кратковременных импульсов.
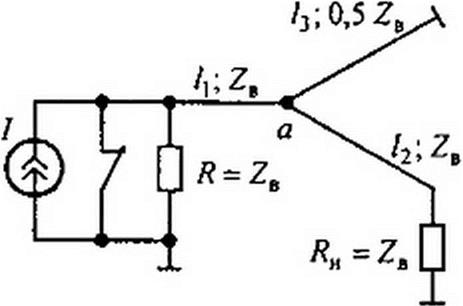
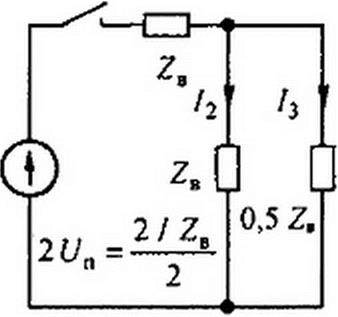
На рис. 12.8, а изображена схема, позволяющая формировать прямоугольные импульсы тока в нагрузке Ян. В схеме имеется источник постоянного тока / и три линии. При размыкании ключа от источника тока / по первой линии длиной /( с волновым сопротивлением Z8 распространяется прямоугольная падающая волна тока //2 и волна напряжения / Ze/2. Дойдя до узла а, волна частично пройдет во вторую и третью линии и частично отразится. Для определения волн, проходящих во вторую и третью линии, служит схема замещения на рис. 12.8, б. Из нее следует, что /2 = / /4 и /} = //2.
 |
|
 |  |
|
 |
По второй линии распространяется волна Uz = /2 ZB, по третьей — 0,5 ZB.
Волна U2, Дойдя до конца второй линии, где включена нагрузка /?и = Z„. поглощается в ней без отражения.
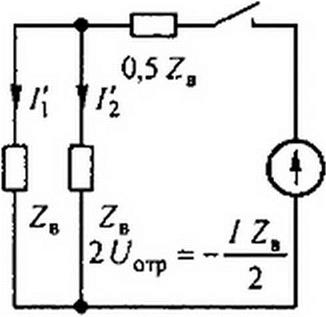
Волна дойдя до короткозамкнутого конца третьей линии, отразится от него с переменой знака у напряжения. Отраженная от конца третьей линии волна напряжения -/0 • 0.5 Z8 = -/ Z„ /2, дойдя до узла а, вызовет токи /2 = /{=-/ /4 в первой и второй линиях в соответствии со схемой замещения (рис. 12.8, в). Волна тока Г} поглощается без отражения в сопротивлении ZB, шунтирующем источник тока. Как только волна тока 1’2 дойдет до конца второй линии, импульс тока в нагрузке Лн прекратится, поскольку токи /2 и /2 равны по величине и противоположны по знаку. Прямоугольный импульс тока через нагрузку появится через время (/, +/2)/и и протекает в течение времени 2/3/и, равного удвоенному времени движения волны по линии длиной /j.
До сих пор в гл. 12 рассматривали переходные процессы в линии, используя метод наложения падающих и отраженных волн, продвигающихся по.линиям без затухания (так как было принято, что Rq = <7о = 0 ). Теперь рассмотрим, как рассчитывают переходные процессы с учетом /?0 и Go.
§ 12.11 Исходные положения по применению операторного метода к расчету переходных процессов в линиях. В линии с распределенными параметрами ток / и напряжение и являются функциями времени и расстояния от начала линии, т. е. i = i(x, и = и(х, Г). Току i(x, t) соответствует операторное изображение /(х, /?), а напряжению u(xj) — операторное изображение (7(х, р).
Кроме того, имеют место соотношения
L0(5/5z) z(x, t) = Lq p /(x, p)\ G^dldt) u(x, f) = G0 p U(x, p).
Имея это в виду, запишем уравнения (11.1) и (11.4) в операторной форме:
-------- = Zo Я*, рУ, (12.36) ах
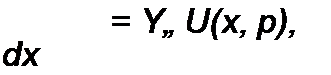 | 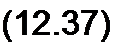 | ||||
 | |||||
(12.38)
(12.39)
Уравнения (12.36) и (12.37) отличаются от уравнений (11.7) и (11.8) тем, что j (а заменено на комплексную частоту р. Из (12.36) и (12.37) следует, что
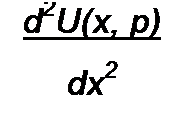 | |||||||||||||||||||||||||
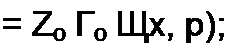 | 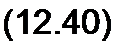 | ||||||||||||||||||||||||
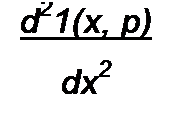 | |||||||||||||||||||||||||
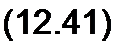 | |||||||||||||||||||||||||
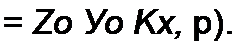 | |||||||||||||||||||||||||
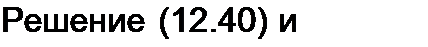 | |||||||||||||||||||||||||
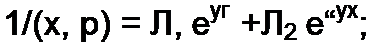 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
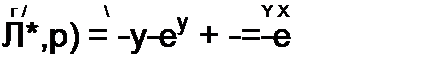 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
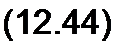 | |||||||||||||||||||||||||
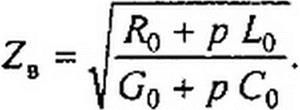 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
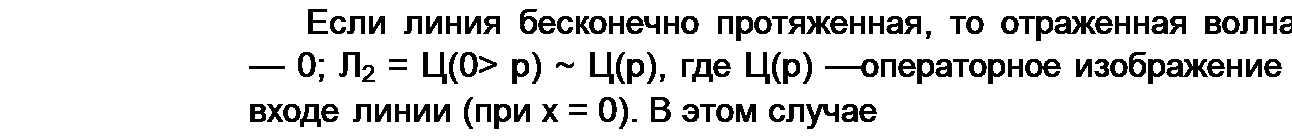 | |||||||||||||||||||||||||
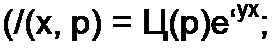 | |||||||||||||||||||||||||
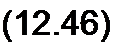 | |||||||||||||||||||||||||
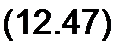
/(*> Р) =
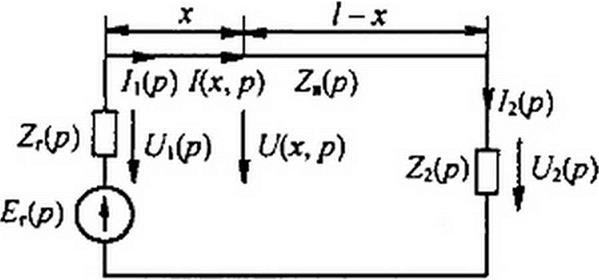
На рис. 12.9 изображена линия длиной /, нагруженная на ZH(p). Напряжение в начале линии — (7|(р), в конце линии — ^2(р)- Напряжение генератора UT(p). Внутреннее сопротивление генератора— Zr(p); х — расстояние текущей точки на линии от начала линии. Операторное
| Рис. 12.9 |
| изображение напряжения и тока в точке х запишем аналогично уравнениям (11.38) и (11.39), заменив в них у на 1-х: |
| U(x, р) = U2 (р) ch у (/ - х) + /2 (р) ZB sh у (/ - х); |
| (12.48) |
| /(х, р) = sh у (/ -х) + /2(р) ch у (/ - х). .4 в |
| (12.49) |
| Т* , , х £Л(р) Ток в нагрузке 12{р) = — ^2 Положим х = 0 и из (12.48), (12.49) получим |
| ^(p)^2(p)(chy/ + -^shy/); Z2 |
| Z|(p) = U2(p) |
| Напряжение генератора |
| ch у / shy/ |
| (12.50) |
| ^г(Р) = Ц(Р)+/1(Р)^г=^2(^) 1 + |
| ch у I + ——l shy/.(12.51) |
| Из (12.51) определим U2(p) и затем 12(р) и подставим и (12.49): |
| их в (12.48) |
| C/r(p): ch у (/-x) + —^ sh у (/-x) t/(x, P) = -7--------------------- .------------------------------------- |
| (12.52) |
| / (x, p) = |
| chy/+ shy/ k z2 / |
| ^r(P) chy(/-x)+ I1 shy (/-x) \ ZB |
| (12.53) |
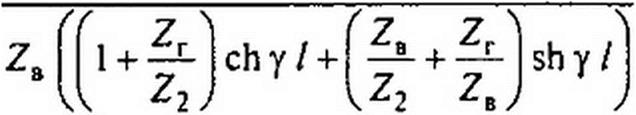
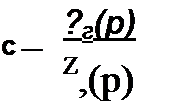
Обозначим а - ; Ь = -г-;
Zh(P)
чения в (12.52) и (12.53). Получим
| U(x,p) = Ur(p) |
| (l + a)eY(/-r) + (l-g)e~Y(/-x) (1 + о + 6 + с)еу/ +(1 +6-а-с)е"',/ ’ |
| / (х, р) = |
| Ur(p) (l + a)eY(/"x)+(o-l)e~Y^x) ZB(p) О + а + Ь + с)еу/ + (1 + Ь-а-с)е~у1 |
| (12.54) (12.55) |
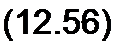
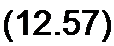
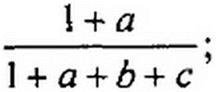 |
|
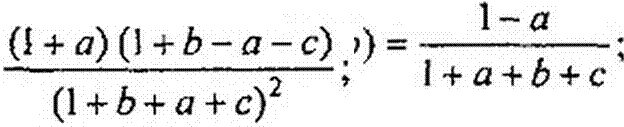 |
|
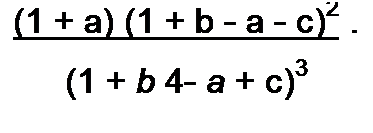 | |||||
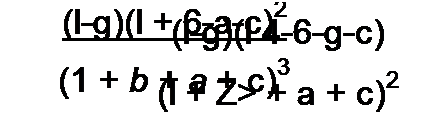 | |||||
 | |||||
Поделив числитель на знаменатель формулы (12.55), получим изображения падающих и отраженных волн напряжения в точке, удаленной на расстояние х от начала линии:
(/(х, р) = Ur(p) (F}(p) е~ух + F2(p) - F3(p) е-у(2/+х) -
- FA(p) е’у(4/-х> + F5 е"у(4/+х) + F6(p) е’у{б/-х) -.,.).
Аналогично для тока:
К*, р) = <F\(P) е'" - 5(Р) е'т(2'~ - F3(p) е'1"2'"’ +
2>(Р)
+ F4(p) e’Y(4/-x) + Fs е-у(4/+х) - F6(p)е-у{61^ -
Здесь
Нахождение функций времени, соответствующих уравнениям (12.56) и (12.57) с учетом того, что t/h Y, Zr, ZB и Z2 являются функциямир, в общем случае оказывается довольно громоздким делом. Поэтому ограничимся рассмотрением лишь нескольких задач.
§ 12.12 Подключение линии без потерь конечной длины /, разомкнутой на конце, к источнику постоянного напряжения. В этом случае Rq =Go =0 ив соответствии с (12.44) и (12.45)
у = Ру /LqCq =р/и; ZB =7^о/С0; Ц(р)^С/ / р.
Обозначим время прохождения волной расстояния / через т0 (т0 =//и) и время х/и через т. Тогда из (12.52) следует, что
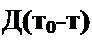 | |||
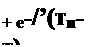 | |||
р ch р т0 р
Поделив почленно числитель на знаменатель, получим
U(x,р) = — + е-'’*2’’"” --е'р<л+ е“/,(4'»*’> + ...).
Р (12.58)
В соответствии с теоремой смещения в области оригиналов (см. § 8.40) от (12.58) перейдем к функции времени
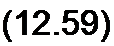 W(x,r) = i/ (1 (/-т) + 1(г-(2 т0-т))-
W(x,r) = i/ (1 (/-т) + 1(г-(2 т0-т))-
-1(/-(2 то+т)) + 1О~(4 т0+т)) —...).
Таким образом, решение для напряжения в произвольной точке записано как сумма падающих и отраженных волн напряжения (что совпадает с решением, полученным в § 12.7 волновым методом), не затухающих по амплитуде. Каждое слагаемое решения вступает в действие, когда аргумент соответствующей единичной функции становится 0.
§ 12.13 Подключение линии без искажения конечной длины 7, разомкнутой на конце, к источнику постоянного напряжения I/. В этом случае
/?0 / - Go / Со - 5, у — (р + 6) >/Aq Cq — (р + 5) / и; Ze — -^Lq/Cq.
Из (12.52) следует, что
... . U сЩр + 6) (I - х»
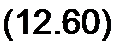 U(X 'P}-p ch((p + 5)VZ^/) =
U(X 'P}-p ch((p + 5)VZ^/) =
_ £ ch(p + 5) (т0-т) = £ e (F *S)(T°~T)-ье'(р*8)(т,|~т)
Р Ch(/? + 5)T0 р e(/’*S)r|1 +е-(/>+8)т„
Поделим почленно числитель на знаменатель и перейдем к функции времени:
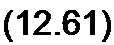 и(х, t) = (7(е"5т 1(г - т) + е“(2тц-т)51(/ - (2 т0 - т))-
и(х, t) = (7(е"5т 1(г - т) + е“(2тц-т)51(/ - (2 т0 - т))-
_е-(2го+х)8 ](,_(2т0+т))-е-(<и,>“т)8 1(7-(4 т0-т))+ ...).
Падающие и отраженные волны теперь затухают по амплитуде по экспоненциальному закону в зависимости от пройденных ими расстоя
ний. Установившееся значение напряжения в конце линии при t -> а> в соответствии с п. 5 § 8.40:
lim pU(l,p) = ----------- ^,Ch ° --------------------------- --------------------------- =.--------------------------- (12.62)
p-о ch(S Со /) ch / Ло у1с0/^
§ 12.14 Подключение бесконечно протяженного кабеля без индуктивности и утечки к источнику постоянного напряжения V. Полагаем, что прямой и обратный провода кабеля близко расположены друг к другу (поэтому £0 -0) и его изоляция между проводами очень хорошая (С?о*О). Тогда согласно (12.44) и (12.45) y^RC р; ZB -^R/C р. Обозначим а = х <JRC и учтем, что Ц(р) -U/р.
По (12.52) и (12.53)
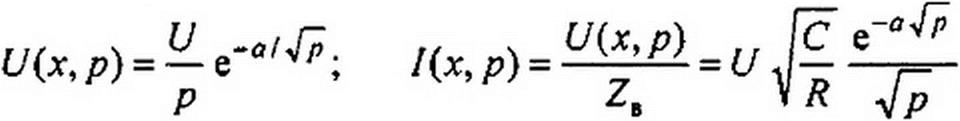 |
|
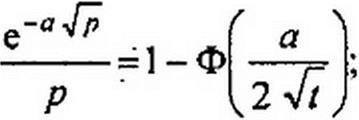 | 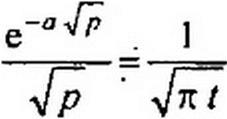 | ||
|
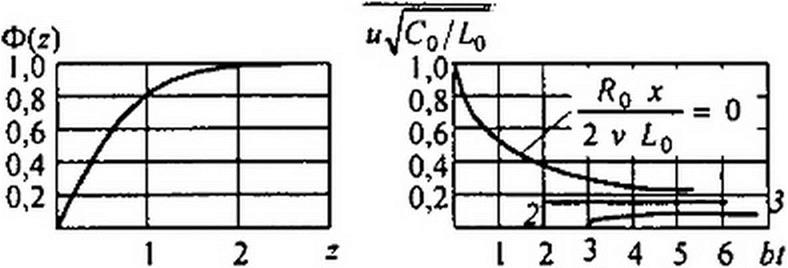
Функция
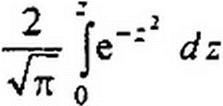 |
|
(в нашем случае z = х <jRC /2 Л = а/2Л ) представляет собой интеграл ошибок Гаусса (рис. 12.10, а).
Решение для напряжения и тока:
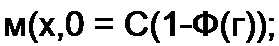 | |||
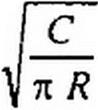 | |||
|
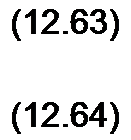 | |||
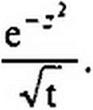 | |||
Отметим, что решение, полученное в предположении, что у кабеля Zo = Go s 0’ имеет два недостатка:
1) напряжение и ток передаются от точки к точке не с конечной, а с бесконечно большой скоростью;
 |
|
2) ток в начале линии в момент включения достигает бесконечно большого значения (в действительности он ограничивается хотя и малым, но конечным сопротивлением источника питания).
3) 12.15. Подключение бесконечно протяженной линии без утечки к источнику постоянного напряжения. Полагаем Go = 0 и из формул (12.44) и (12.45), обозначив v = y/LC; b = R$l2LQ, определим
у = yl(RQ + р LQ) рС0 = -^р7 +2Ь р\ и
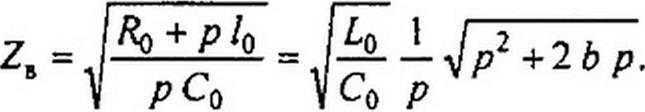 |
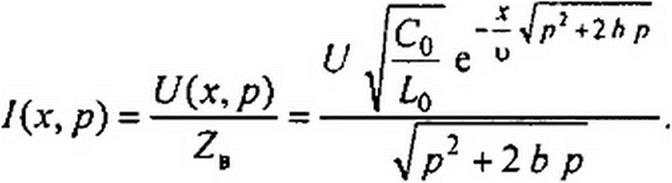 |
|
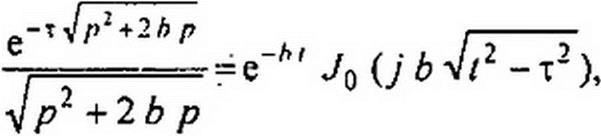 |
Изображение напряжения в начале линии Ц (0, р) -U / р. В соответствии с формулами (11.37) и (11.38) изображение напряжения и тока в точке, удаленной на расстояние х от начала линии,
... X
U(x,p) = — е
Р
Для определения тока /(х, /) как функции времени / и расстояния х (для t >х/и = т) воспользуемся табличным соотношением:
где Jq (у b Nt2 — т2) — бесселева функция нулевого порядка от мнимого аргумента. Значения ее приведены в табл. 15.1. Следовательно,
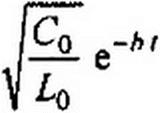 |
|
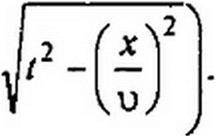 | |||||
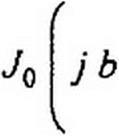 | |||||
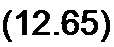 | |||||
В соответствии с (12.65) на рис. 12.10, б изображена зависимость
'(у) = ДЬ I) = /(~1 . fa U£o J ! ^0
Из рисунка видно, что при малых х (малых RQ х/(2 и До)) ток i, получив большой начальный толчок, уменьшается во времени. При больших значениях х ток / после скачка сначала возрастает, а затем умень-
шается. Так как для линии с распределенными параметрами, у которой
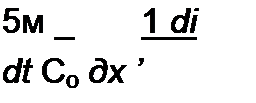 | |||||||||||||
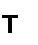 | |||||||||||||
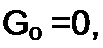 | |||||||||||||
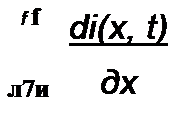 | |||||||||||||
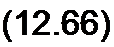 | |||||||||||||
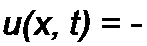 | 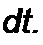 | ||||||||||||
Возьмем частную производную от i(x,t) (см. (12.65)) по х, подставим ее в (12.66) и учтем также напряжение, обусловленное скачком тока на фронте волны. В результате получим
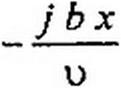 |
|
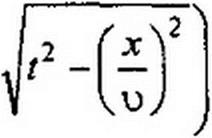 | |||||||
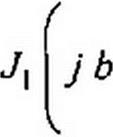 | |||||||
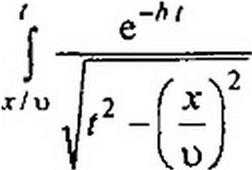 | |||||||
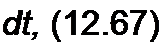 | |||||||
где J} — функция Бесселя первого порядка от мнимого аргумента (см. табл. 15.1). Слагаемое е"Лх/и в (12.67) соответствует скачку тока на фронте волны. На фронте волны в точке х в момент х/у ток равен 1с~ —
U ~ е u , а в соседней точке х + Дх в тот же момент времени ток еще отсутствует. Поэтому напряжение, вызванное скачком тока на фрон
те волны,
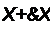 | |||||||
 | |||||||
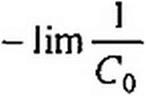 | |||||||
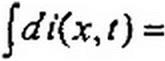 | |||||||
|
, с. pi hx Ьх
------ i(x, i) х &х = - 0 + —- ° - е и = U е и . у Со * у Со
Вопросы для самопроверки
§ 1.1 каких допущениях на первом этапе изучения рассматривают переходные процессы в линиях с распределенными параметрами? Какими дифференциальными уравнениями описывают эти процессы? 2. Как понимать, что аргументами функций,, являющихся решением, оказываются (z-x/и) и (г + х/и)? 3. Как показать, что для линии без потерь характер изменения и или i падающей волны а любой точке линии повторяет характер изменения и и i в начале линии, но с запозданием во времени? 4. Как согласовывают переходные процессы в линиях с распределенными параметрами с переходными процессами в нагрузке на конце линии? 5. Обосновать методику составления схем замещения для исследования волновых процессов, когда волна дойдет до нагрузки. 6. Как из временных графиков напряжения и„ на нагрузке и тока iH в нагрузке получить графики отраженных волн и0 и i0 на линии? 7. Какова идея расчета переходных процессов в линии с распределенными параметрами при отключении нагрузки или части ее? 8. Охарактеризуйте стадии волнового процесса при подключении разомкнутой на конце линии длиной / к источнику постоянного напряжения, полагая сначала для линии /?о =Gq =0, а затем, что линия является линией без искажения. 9. Как от уравнений для мгновенных значений тока и напряжения перейти к уравнениям, записанным для операторных изображений этих величин? 10. В каком случае в качестве линии задержек используют линию с распределенными параметрами, а в каком — каскадное соединение фильтров ИЧ? 11. Объясните идею формирования кратковременных импульсов с помощью линии с распределенными параметрами. 12. Решите задачи 15.5; 15.6; 15.12; 15.17.
Глава тринадцатая








