§ 12,2. Исходные уравнения и их решение. Из уравнений (11.1) и

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

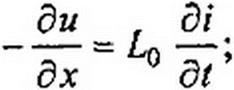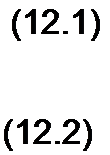(11.4) при R_o =0 и G_q -0 следует, что

Э/ _ ди а7-^с° dt

Ток и напряжение являются функциями двух переменных: расстояния х от начала линии и времени t. Продифференцируем (12.1) по х и (12.2) ПО Г.

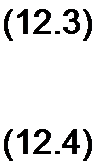д²и _ d²i дх² ° дх дГ d²i „ д²и dxdt~~ ⁰ ~дР‘

В соответствии с (12.4) в правую часть (12.3) вместо d²i/dxdi под- и

ставим -С_о —j- и обозначим А_о С_о = 1/и²:

д²и _ 1 д²и дг и² dt²

Из предыдущего (см. §11.10, формула (11.44)) известно, что и = 1/ VЛо С_о ^есть скорость распространения электромагнитной волны по линии. Если уравнение (12.2) продифференцировать пох, а (12.1) — по I и в правую часть продифференцированного уравнения (12.2) под­ставить правую часть продифференцированного уравнения (12.1), то получим

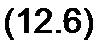d²i 1 d²i

~ V* 5” ’С? ‘ ох~ и" дг

Уравнения (12.5) и (12.6) — это уравнения второго порядка в част­ных производных. Из курса математики известно, что уравнения такого вида называют волновыми.

Решением уравнения (12.5) является сумма любых функций / и /₂> причем аргументом функции f\ является (z-x/u), а аргументом функ­ции /₂ является (f + x/v):

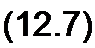и (/-х/и) + /> (г + х/о).

Для сокращения записи в дальнейшем будем обозначать:

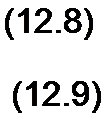“п =/i (‘-x/v);

«о =/2 (t + x/v).

Следовательно,

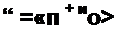(12.10)

где индексы «о» и «п» означают «отраженная» и «падающая» (волны).

Вид функций f и f₂ определяется граничными условиями в начале и конце линии. Функции / и /₂ в общем случае должны позволять дважды дифференцировать их по х и t.

Подстановка функций /}(/-х/и) и /₂(1 + х/и) в (12.5) дает тожде­ство.

Решение уравнения (12.6):

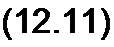
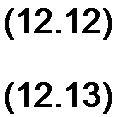i = (р| (Z - х / и) + ф₂ G + х! и).

Для сокращения записи обозначим:

/_п =q>i (z-x/v);

/_о = ф₂ (Z + X/v).

Тогда

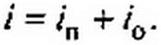(12.14)

§ 12.3 Падающие и отраженные волны на линиях. В соответствии с формулами (12.7) и (12.11) напряжение и ток в линии могут быть пред­ставлены в виде двух функций: функции / (z-x/u) и ф₍ (z~x/v) — падающие волны; функции /₂(z + x/v) и ф₂(/ + х/о) — отраженные волны.

Падающие волны перемещаются со скоростью v по направлению от источника энергии к приемнику, т. е. в сторону увеличения координаты х; отраженные волны — от приемника энергии к источнику, т. е. в сторо­ну уменьшения координаты х.

Обсудим, как следует понимать, что аргументом функции /j является (z-x/v) (аналогичные выводы можно сделать и по отношению к дру­гим функциям).

Пусть в некоторой точке линии при х = х₍ и z -значение функции J\ (z^Xj/v) равно fj. Это значение функция j\ будет принимать во всех точках линии, где х > х, с запозданием во времени, равным (x-xj/v и обусловленным конечной скоростью перемещения волны по линии.

Так, в точке х-х₂ значение функции f_} будет равно при t = t₂ = t_} + (х₂ - Х|)/ и. Действительно,

f\ (*2 - ^х2 /^и) ~ /1 ⁺ "* f\ ~

Таким образом, каков бы ни был закон изменения напряжения пада­ющей волны / в начале линии, по такому же закону, но с запозданием во времени изменяется напряжение падающей волны в любой точке ли­нии.

§ 12.4 Связь между функциями /_р /₂ и функциями ф_р ф₂.

Найдем связь между функциями и ф₍, а также /₂ и ф₂- С этой це­лью в (12.1) и (12.2) подставим (12.7) и (12.11) и для сокращения записи

обозначим:

Тогда уравнение (12.1) дает

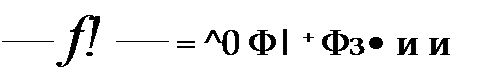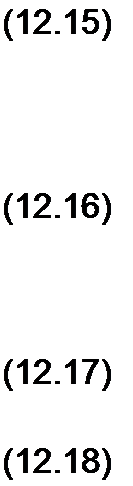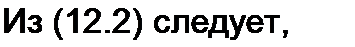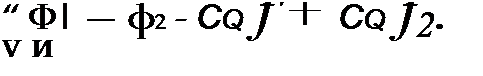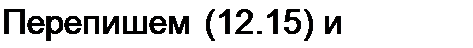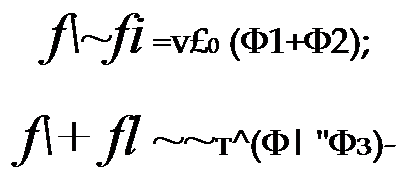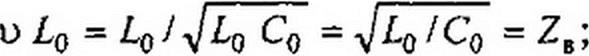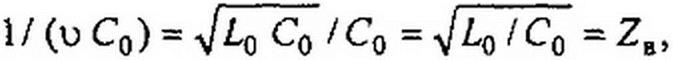где Z_B — волновое сопротивление однородной линии без потерь (см. формулу (11.26)).

Таким образом,

/'-/₂'=Z_B (ф;+ф;);

Z^Z+/2=^_B (Ф1-Ф2).

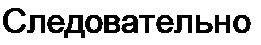(12.21)

(12.22)

Если производные двух функций (например, ср] и /,') при любых значениях х и / равны, то это значит, что сами функции (cpj и f ) равны с точностью до постоянной. Поэтому

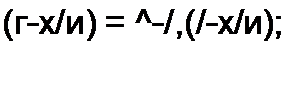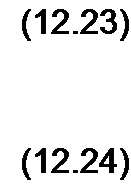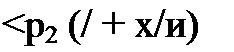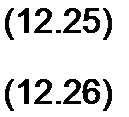Постоянные интегрирования опустили, так как полагаем, что в токах и напряжениях падающей и отраженной волн отсутствуют постоянные составляющие, не зависящие от х и от t. Два последних уравнения мож­но переписать с учетом (12.8), (12.9), (12.12), (12.13):

^fn ^МП ' ^ZB>

^0 ='^wo^/ZB-

Из (12.25) следует, что ток падающей волны для любого момента вре­мени и для любой точки на линии равен частному от деления напряже­ния падающей волны для того же момента времени и для той же точки линии на волновое сопротивление.

Из (12.26) вытекает, что ток отраженной волны для любого момента времени и для любой точки линии равен взятому с обратным знаком ча­стному от деления напряжения отраженной волны в той же точке линии и для того же момента времени на волновое сопротивление. Знак минус в (12.26) означает, что ток отраженной волны направлен встречно поло­жительному направлению отсчета тока, показанному на рис. 11.2.

§ 12.5

Электромагнитные процессы при движении прямоугольной волны по линии. Пусть источник постоянного на­пряжения и_у имеющий внутреннее сопро­тивление, равное нулю, подключается к незаряженной однородной линии с распре­деленными параметрами, у которой j%=G_o=0 (рис. 12.1).

По линии перемещается падающая электромагнитная волна. Начальный уча­сток волны, первым продвигающимся по

линии, принято называть фронтом волны. В данном случае волна имеет прямоугольный фронт.

Двигаясь по линии, волна создает между проводами линии электри­ческое и магнитное поля.

Приращение магнитного потока (потокосцепления) на фронте волны за время dt равно произведению тока / на индуктивность участка линии длиной dx: dy = i L_o dx; оно вызывает ЭДС

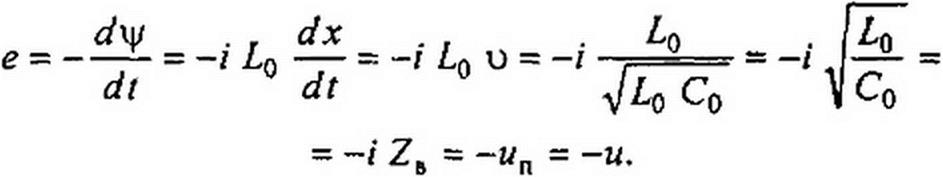
Таким образом, на фронте волны возникает ЭДС самоиндукции, чис­ленно равная напряжению генератора. На фронте волны происходит за­рядка проводов линии: один провод, например верхний, присоединенный к плюсу источника ЭДС, приобретает положительный заряд, другой (ниж­ний) — отрицательный заряд (такой же величины).

Кроме того, на фронте волны возникает ток смещения /_см = dq! dt, где dq — приращение заряда на одном из проводов линии за время dt:

dq = С_о и dx - Cq и и dt.

Проходящий по диэлектрику на фронте волны ток смещения равен току падающей волны, проходящему по проводам линии:

'см ~ ~ Q ^{и и} ~ ~

^см dt ⁰ Z_B

Электромагнитная волна, продвигаясь по линии, каждой единице дли­ны ее сообщает энергию электрического поля С_о /2 и энергию маг­нитного поля L_q /2. Можно показать, что эти количества энергий рав­ны. Действительно,

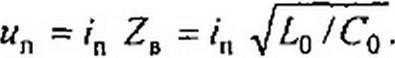
Следовательно,

С_о и^г„ /2 = С„ i- L_o /(2 С_о) = £о 'п²/2.

Когда падающая волна достигает конца линии, к которому в общем случае присоединена некоторая нагрузка или другая линия (с другим волновым сопротивлением), то часть падающей волны проходит в нагруз­ку (или соответственно во вторую линию), а часть отражается — возни­кает отраженная волна.

Чтобы выяснить, какова форма волны, проходящей в нагрузку, како­ва форма отраженной волны и как они деформируются во времени, при­меняют расчетную схему, которую принято называть схемой замещения для исследования волновых процессов в линии с распределенными пара­метрами.

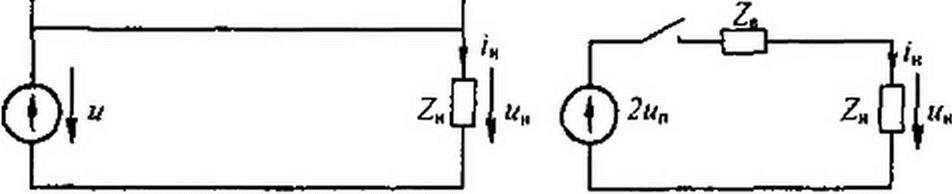
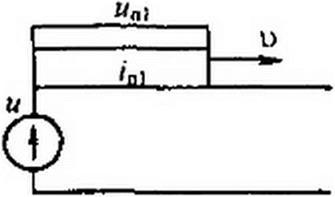
§ 12.6 Схема замещения для исследования волновых процессов в линиях с распределенными параметрами. Для обоснования методики составления схемы замещения обратимся к рис. 12.2, а. На нем изобра­жена линия с распределенными параметрами, на конце которой включе­на некоторая нагрузка. Начиная с того момента, когда падающая волна дойдет до конца линии, по нагрузке пойдет ток /_н и на ней будет напря­жение и_н. п

На рис. 12.2, а изображены эпюры волн и и i на линии для момента времени, непосредственно предшествующего подходу волны к концу линии.

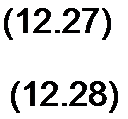В соответствии с формулами (12.10) и (12.14) напряжение и ток в любой точке линии можно представить в виде суммы падающих и отра­женных волн. Это справедливо также в отношении напряжения и тока в конце линии. Следовательно,

^wn ^{+ М}О ’
'п⁺'о=Ч*

Заменив /_п на w_n/Z_B, а /₀ на - м₀/Z_B, получим

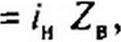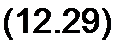или

2 w= u_u + L Z„.
II <1 п п

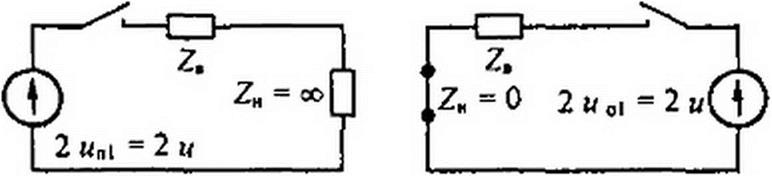
Таким образом, напряжение на конце линии и_п и ток в нагрузке i_n независимо от характера нагрузки связаны с напряжением падающей волны и_п уравнением (12.29). Последнему соответствует схема с сосре­доточенными параметрами, изображенная на рис. 12.2, б. В ней к источ­нику ЭДС напряжением 2w_n подключают последовательно соединенные Z_B и Z_H.

Расчет переходного процесса в схеме с сосредоточенными парамет­рами (рис. 12.2, б) выполняют любым из методов, рассмотренных в гл. 8. Расчет дает возможность определить /_н = f(f) и w_H = f(t). После того как эти зависимости найдены, можно определить характер изменения во
времени напряжения и тока отраженной волны: и₀ - f(t) и i_(/ - /(t). Действительно, из уравнений (12.27) и (12.26) следует, что

"о (О - ^и» (О - ^и п (0;

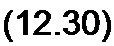2, ⁼ V •

Рассмотрим несколько примеров, иллюстрирующих применение схе­мы замещения.

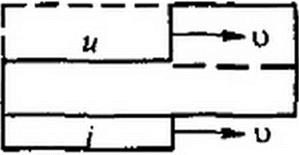
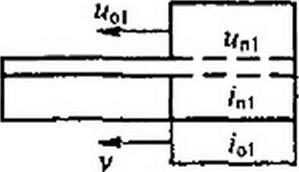
§ 12.7. Подключение разомкнутой на конце линии к источнику постоянного напряжения. В линии без потерь, так же как и в колеба­тельном контуре без потерь, при подключении к источнику постоянной ЭДС возникают незатухающие колебания. Период колебаний состоит из четырех частей или стадий (рис. 12.3, а-г) одинаковой продолжительно-

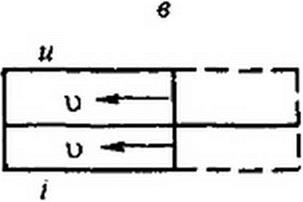Рис. 12.3

сти //и, где I — длина линии, и— скорость распространения волны. Для рассмотрения этих стадий воспользуемся двумя различными схема­ми замещения. Первая схема (рис. 12.4, а) соответствует разомкнутому концу линии (Z_H - <ю), когда к нему подходит падающая от начала ли­нии волна. Вторая схема (рис. 12.4, б) соответствует моменту времени, когда отраженная волна подошла к началу линии, где включен генератор постоянного напряжения, внутреннее сопротивление которого полагаем равным нулю (Z_H = 0).

Рассмотрим каждую из стадий процесса в отдельности.

Первая стадия. От генератора к концу линии распространяются вол­на напряжения м_П| = и и волна тока /_п{ = u_nl /Z_B = / (см. рис. 12.3, а).

Вторая стадия заключается в том, что от конца линии к ее началу движется отраженная волна (w₀₁, /_о1). Для определения а₀₁ и служит схема рис. 12.4, а. Она составлена в соответствии с общим методом, изложенным в § 12.6. В ней к напряжению 2 и_п, = 2 и подключаются вол­новое сопротивление линии Z_B и сопротивление нагрузки Z_H = оо (ли­ния на конце разомкнута!).

Согласно рис. 12.4, а напряжение на нагрузке равно удвоенному напряжению падающей волны. Действительно, при Z_H

u_z -2м_п1——— = 2«_ni=2w.

_и п I 1 ИI

Н 8

В соответствии с формулой (12.30) отраженная волна напряжения

«о1 =«н -«Hi =2w_nl -л_п1 =м;

в соответствии с формулой (12.26) отраженная волна тока

*О1 ~ ~«01 ^8 ~ ^-/П1 ~

Таким образом, в течение второй стадии процесса от конца линии к началу продвигается отраженная волна н₀₍ = м, /_о1 = Результирующее состояние на линии определяется наложением первой падающей волны (w_nl, /_п1) и первой отраженной волны (w_ob /_о1). На рис. 12.3, б дана эпюра распределения напряжения и тока по линии для некоторого мо­мента времени во второй стадии. (В этой стадии для участков линии, на которые прошли отраженные волны, результирующее напряжение равно 2 и, а результирующий ток равен нулю.)

Третья стадия процесса состоит в том, что волна н_о), /_о1, дойдя до начала линии, отразится от генератора, как от короткозамкнутого конца линии (внутреннее сопротивление генератора принято равным нулю), и вызовет распространение в направлении от генератора к концу линии второй падающей волны {и_п2, Z,^), являющейся, по существу, отражен­ной волной по отношению к волне (u_ob /_о1).

Для определения характера отражения волн от начала линии исполь­зуем схему рис. 12.4, б. В ней Z_H =0, 2и_о) -2 и. Так как нагрузка Z_K =0, то и напряжение на ней равно нулю. Но напряжение на нагрузке в соответствии с (12.27) равно сумме напряжения падающей волны (в данном случае u_ol = и) и напряжения отраженной от начала линии вол­ны, распространяющейся от генератора к концу линии и потому назван­ной второй падающей волной. Следовательно, 0 = w + w_n2. Отсюда

«п2 = 'п2 = «п2 ¹ A =

Результирующее состояние на линии по время третьей стадии процес­са изображено на рис. 12.3, в. Оно получено в результате наложения трех волн: первой падающей волны (ц_п1, /_п1), первой отраженной от конца волны (w₀₁, i_ol ) и второй падающей волны (н_п2, *_rt2)-