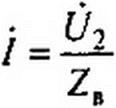§ 11.12 Линия без искажений. Линия без искажении представляет собой линию, вдоль которой волны всех частот распространяются с оди­наковой фазовой скоростью и затухают в равной степени.

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

При движении электромагнитной волны по линии без искажений волны напряжения и тока уменьшаются по амплитуде, но формы волн напряжения в конце и начале линии подобны; точно так же подобны фор­мы волн тока в начале и конце линии.

Неискажающие линии находят применение в телефонии. При телефон­ном разговоре по таким линиям не искажается тембр голоса, т. е. не искажается спектральный состав голоса.

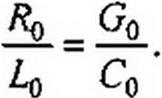Для того чтобы линия была неискажающей, коэффициент затуха­ния а и фазовая скорость и_ф не должны зависеть от частоты; а и и_ф не зависят от частоты, если между параметрами линии имеет место следующее соотношение:

(11.46)

Для сокращения записи обозначим R_Q/Л_о = G_o/C_o - к. По определе­нию,

^zo = ^R o + J w Lq = (k + j <o);

^0 “ ^0 ⁺ J ® G) ^— G) ⁺ 7 ®Y>

Y = (k + j<$) yl L_qC₀.

Следовательно,

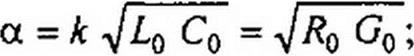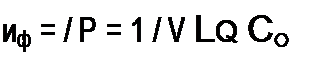Из формул (11.47) и (11.48) следует, что коэффициент затухания а и фазовая скорость и_ф в линии без искажений действительно не зависят от частоты.

В линии без искажений волновое сопротивление является действительным числом и также не зависит от частоты.

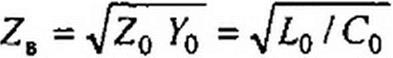Чтобы убедиться, что форма волны напряжения в конце линии у₂ полностью подоб­на форме волны напряжения в начале линии возьмем напряжение на входе линии в виде суммы двух синусоидальных колебаний, одно из которых имеет частоту ш, а другое 2 со, и составим выражение для у,. Пусть

«I = U_lm sm(ai + w_t) + U_2m sin(2<D/ + y₂).

Так как для линии без искажения коэффициент затухания а не зависит от частоты (см. формулу (11.47)), то амплитуды обоих колебаний на расстоянии / уменьшаются в оди­наковой степени и становятся равными е^-а/ и U_2m е^-а/.

Для линии без искажения коэффициент фазы 0 прямо пропорционален частоте, по­этому для частоты 2 w коэффициент 0 в два раза больше, чем для частоты оз.

Следовательно, мгновенное значение напряжения в конце линии

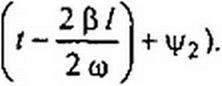
«2 = е^-а/ sin(co/ + ф, -0 /) + U_2n, е“^а/ sin(2 co t + ц/₂ -2 0/) =

sin(co /

Вынесем е’^а/ за скобку и обозначим i-~ через т.

о

Получим

и₂ = e’^a/(U_ln, sin((OT + 4>i) + 0'2_m sin(2<о т + ц/₂)•

Если сопоставить последнее выражение с и₍, то можно сделать вывод, что напряже­ние в конце линии имеет ту же форму, что и напряжение в начале линии. Однако оно умень-

0/ /

шено по амплитуде за счет затухания и смещено во времени на — = — — на время движения волны по линии длиной /.

В реальных линиях передачи сигналов соотношение (11.46) обычно не соблюдается, так как £₀ < Rq C_q/G_q. Для того чтобы было достигну­то это соотношение, принимают меры по увеличению £₀. Практически устранения частотных искажений сигнала во всем передаточном тракте часто достигают не за счет использования линий без искажения, а вклю­чением в тракт специальных корректирующих четырехполюсников.

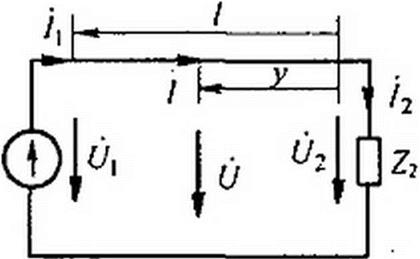
§ ПЛЗ. Согласованная нагрузка. Линия с распределенными пара­метрами, как правило, служит в качестве промежуточного звена между источником энергии (сигнала) и нагрузкой.

Обозначим сопротивление нагрузки Z₂ (Z₂ = ^2^2) (Р^ис- Н.7, а). Если Z₂ * Z_s, то падающая волна частично пройдет в нагрузку, частич­но отразится от нее (возникает отраженная волна). При Z₂=Z_b — такую нагрузку называют согласованной — отраженная волна отсут­ствует. В этом можно убедиться с помощью формулы (11.46). Действи­тельно, отраженная волна отсутствует, так как - 0.

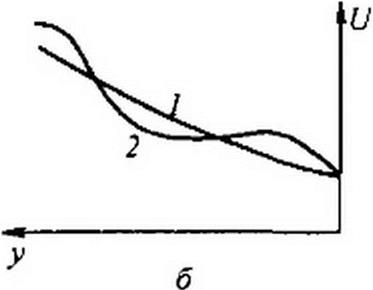Рис. И.7

В линиях передачи информации кроме согласования Z₂ с Z_B согла­совывают также Z_B с внутренним сопротивлением источника сигнала Z_H. При Z_H, немного не равном Z_B, кроме истинного сигнала через
некоторое время после него может появиться ложный сигнал типа эха; наличие последнего затруднит обработку получаемой информации.

§ 11.14 Определение напряжения и тока при согласованной на­грузке. Чтобы получить формулы для определения напряжения и тока в любой точке, удаленной от конца линии на расстояние у, в формулы (11.38) и (11.39) вместо Z_B подставим Z₂, заменим /₂ Z₂ на й₂ и f/₂/Z₂ на /₂. Получим

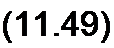
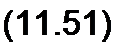U -U₂ (ch у >> + shy y)-U₂ ^&УУ>

/ = /₂ (ch у у + shy у) = /₂

В начале линии при у - I

U = U₂e'^,y=U₂e^JV‘^:‘ е'е^¹; i = i,^>’ = I₂ е'*'> е^а'е'^₽'_>

где U₂ — модуль; 4>и₂ — аргумент комплекса [)₂; Л — модуль; Ф/₂ — аргумент комплекса /₂.

График зависимости действующего значения напряжения U от рассто­яния у для линии с потерями при согласованной нагрузке иллюстрирует рис. 11.7, б, кривая /, при несогласованной, например, кривая 2.

§ 11.15 Коэффициент полезного действия линии передачи при дачи равен отношению активной мощности в конце линии Р₂ ^к актив­ной мощности в начале линии :

Р₂ = (7₂ /₂ со$(фр₂ -Ф/₂) = (7₂ Л ^С05Фв>

где ф_в — аргумент волнового сопротивления Z_B.

При согласованной нагрузке угол между (7, и 1_} также равен <р_й, поэтому в соответствии с формулами (11.51)

Р\ 1\ соз(ф_{/₂ -Ф/_:) = 6^Г₂ /₂ e^2a'cos<p_B

Следовательно,

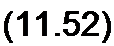г, = Р₂//> = е^-2а/.

§ 11.16 Входное сопротивление нагруженной линии. На рис. 11.7, a изображена схема, состоящая из источника напряжения Ц, линии с рас­пределенными параметрами длиной / и нагрузки Z₂. Входное сопротив­ление Z_BX ={7, //[. В формулах (11.38) и (11.39) вместо^ подставим / и заменим й₂ на /₂ Z₂.

Получим

_ 1₂ Z₂ ^chY 1 + h ^Z3 sh?I

^BX “ _f у ♦ ¹

/₂ ~shy/ + /₂ chy/

^0

или

Z„ = ^z^^chY^z + Z„shy/. (11.53)

sh у I + ch у I

Если нагрузка согласована (т. е. Z₂ = Z_B), то из (11.53) следует, что входное сопротивление равно волновому: Z_BX = Z_B.

§ 11.17 Определение напряжения и тока в линии без потерь. Стро­го говоря, линий без потерь не существует. Однако можно создать линию с очень малыми потерями (с очень малыми R$ и <7₀ по сравнению с ш £₀ и (оС_о соответственно) и распространить на нее теорию линий без потерь.

Из предыдущего (см. формулу (11.21)) известно, что если Я_о - 6₀ = О, то

y = a+j^^j(j)ylL_Q С_о,

т. е. коэффициент затухания а = 0, а коэффициент фазы 0 ~ <n

При этом волновое сопротивление Z_B = JLq/Cq является чисто ак­тивным (см. формулу (11.26)).

Для определения напряжения U и тока / в любой точке линии об­ратимся к формулам (11.38) и (11.39):

й = й₂ chyy + /₂ Z_B shy у;

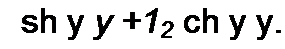Учтем, что у у = (а + j 0) у - jfiy.

Гиперболический косинус от мнимого аргумента j х равен кругово­му косинусу от аргумента х:

ch j х = 0,5(e^{y v} + e“^JX) = 0,5 (cosx + ysinx + cosx-у sinх) = cosx.

Гиперболический синус от аргумента ух равен круговому синусу от аргумента х, умноженному на у:

sh у х = 0,5 (е^{7 х} -е~^{7 х}) - 0,5 (cosx + у sin х- cosx + j sin х) =* у sin х.

Следовательно, sh у х = sh j 0 у = у sin 0 у.

Поэтому для линии без потерь формулы (11.38) и (11.39) перепишем следующим образом:

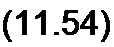
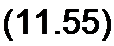U = U₂ cosp у + j 1₂ Z_B sinp у;
♦

/ - j — sin p у + /₂ cos p y.

§ 11.18 Входное сопротивление линии без потерь при холостом ходе. При холостом ходе = 0. Поэтому

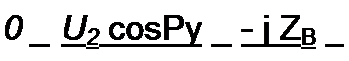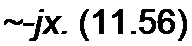Исследуем характер изменения Z_BXX при изменении расстояния у от конца линии до текущей точки на ней и проиллюстрируем это рис. 11.8, а.

В интервале значений Р у от 0 до к/2 tgpy изменяется от 0 до <ю, поэтому Z_BXX имеет емкостный характер (множитель -j) и по модулю изменяется от со до 0. Расположение кривой выше оси абсцисс соответ­ствует индуктивному характеру реактивного сопротивления линии х, ниже оси — емкостному. В интервале значений Ру от л/2 до л tgpy отри­цателен и изменяется от -ас до 0, поэтому Z_BXX изменяется по модулю от 0 до оо и имеет индуктивный характер (множитель + J) и т. д.

Конденсаторы или индуктивные катушки, изображенные на рис. 11.8, а, иллюстрирует характер входного сопротивления х.

Таким образом, изменяя длину отрезка линии без потерь, можно ими­тировать емкостное и индуктивное сопротивления любой величины.

Практически это свойство используют при высокой частоте в различных радиотехнических установках.

§ 11.19 Входное сопротивление линии без потерь при коротком замыкании на конце линии. При коротком замыкании на конце линии U2 =0 и из формул (11.54) и (11.55) следует, что входное сопротивле­ние

2_ВХХ ⁼ А tg3= 7 7Л) /Q tg0У, (11.57)

где 0 = о yj Z,g / С_о .

Будем изменять длину отрезка линии у и исследуем характер входно­го сопротивления.

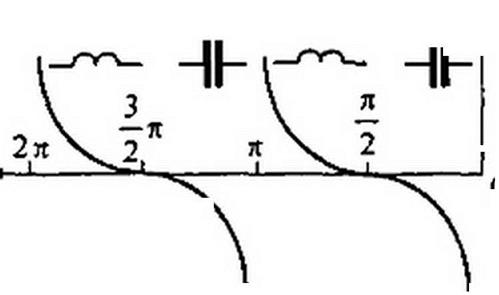
В интервале значений 0 у от 0 до тс /2 tg 0 у положителен и изме­няется от 0 до со, следовательно, в этом интервале входное сопротивле­ние имеет индуктивный характер и по модулю изменяется от 0 до со (рис. 11.8, б).

В интервале 0у от л/2 до л входное сопротивление имеет емкост­ный характер и изменяется по модулю от оо до 0 (в точке 0у = л/2 tgfiy скачком изменяется от -н» до -со).

Таким образом, изменяя длину отрезка короткозамкнутой на конце линии, также можно создавать различные по величине индуктивные и емкостные сопротивления. Отрезок короткозамкнутой на конце линии без потерь длиной в четверть длины волны теоретически имеет входное со­противление, равное бесконечности. Это позволяет применять его при подвеске проводов в качестве изолятора.

§ 11.20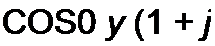

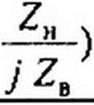
Входное сопротивление линии без потерь при реактивной нагрузке. Определим входное сопротивление линии без потерь при чис­то реактивной нагрузке Z_H - j Х_н:

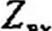
Z_H cos0y + Z_B sin p у Z cos 0 у + j —- sin 0 у

Обозначим -j Z_H /Z_a = tg v и учтем, что

,_{g(3 у+v)}=. l-tg0^tgv

Получим

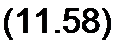Z„ = j z, ^tg *^{tg V} = j z. tg(P у + v), 1 - tg V tg 0 у

т. e. входное сопротивление изменяется по тангенсоиде, начало которой смещено на угол v.

При индуктивной нагрузке

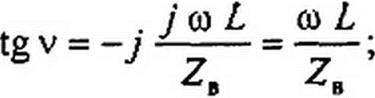при емкостной

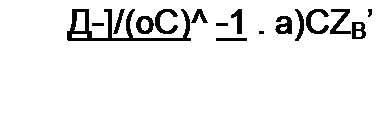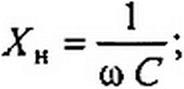§ 11.21 Определение стоячих электромагнитных волн. В линиях без потерь при холостом ходе, коротком замыкании, а также при чисто реактивных нагрузках возникают стоячие электромагнитные волны.

Стоячая электромагнитная волна образована стоячими волнами напряжения и тока. Математически такие волны описываются произве­дением двух периодических (в нашем случае — тригонометрических) функций. Одна из них — функция координаты текущей точки на линии (в нашем случае — Р у), другая — функция времени (о /). Стоячие вол­ны напряжения и тока всегда сдвинуты по отношению друг к другу в про­странстве и во времени.

Сдвиг во времени между стоячими волнами напряжения и тока равен 90°, сдвиг в пространстве — четверти длины волны (см. формулы (11.62) и (11.63), (11.65) и (11.66)).

Точки линии, где периодическая функция координаты проходит через нуль, называют узлами, а точки линии, в которых периодическая функ­ция координаты принимает максимальные значения, — пучностями.

При возникновении стоячих волн электромагнитная энергия от нача­ла к концу линии не передается. Однако на каждом отрезке линии, равном четверти длины волны, запасена некоторая электромагнитная энергия.

Эта энергия периодически переходит из одного вида (энергии элект­рического поля) в другой (энергию магнитного поля).

В моменты времени, когда ток вдоль всей линии оказывается равным нулю, а напряжение достигает максимального значения, вся энергия пе­реходит в энергию электрического поля.

В моменты времени, когда напряжение вдоль всей линии равно нулю, а ток достигает максимального значения, вся энергия переходит в энер­гию магнитного поля.

§ 11.22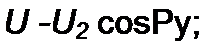

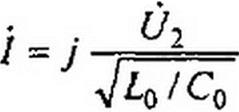
Стоячие волны в линии без потерь при холостом ходе линии. Из формул (11.54) и (11.55) следует, что при холостом ходе

(11.59)

(11.60)

Для перехода к функциям времени умножим правые части формул (11.59) и (11.60) на 41 е^уШ и от полученных произведений возьмем мни­мые части:

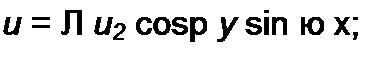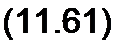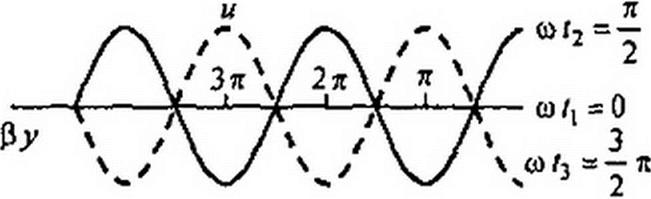
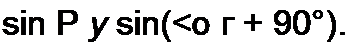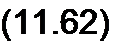Угол 90° в аргументе у синуса в формуле (11.62) соответствует мно­жителю j в формуле (11.60).

В точках ру = Ая, где А = 0,1,2,..., будут узлы тока и пучности напряжения.

Рис. Н .9

График стоячих волн напряжения и тока для трех смежных моментов 3

времени со /] = 0, со /₂ = л/2, со t₃ = — л показан на рис. 11.9: а — напря­

жения, б — тока. Сплошными линиями обозначена волна при со/, =0,

3

тонкими — при со /₂ -л/2, штриховыми — при со /₃ = - я для напря­

жения и при со /₃ = л для тока.

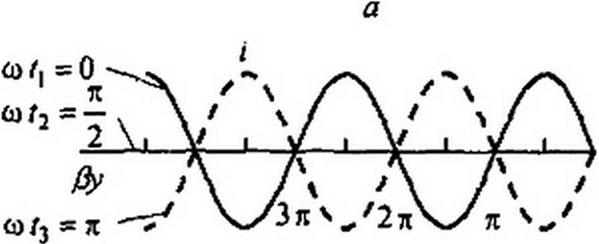
§ 11.23 Стоячие волны в линии без потерь при коротком замы­кании на конце линии. Из формул (11.54) и (11.55) следует, что при ко­ротком замыкании на конце линии

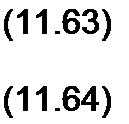(j = j i₂ ^z Q ^sin P z;

/ = /₂ ^co$ P У-

Для перехода к мгновенным значениям умножим правые части формул (11.63) и (11.64) на V2 е^{у и}' и от произведений возьмем мнимые части:

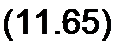
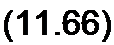U = 41 1₂ л /Lq/Cq sin Р у sin(co t + 90°);

/ = 41 /₂ cosP у sin со t.

В правой части формулы (11.65) — в формуле для напряжения — есть множитель sin р у sin(co t + 90°), как и в формуле (II .62) для тока Л

Следовательно, картина стоячей волны напряжения при коротком за­мыкании на конце линии качественно повторяет картину стоячей волны тока при холостом ходе линии.

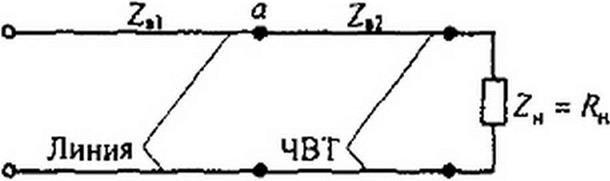
§ 11.24 Четвертьволновый трансформатор. Для согласования линии без потерь, имеющей волновое сопротивление Z_B1, с активной на­грузкой Z_H = /?_к Z_B| применяют четвертьволновый трансформатор (ЧВТ). Он представляет собой отрезок линии без потерь длиной четверть волны Л./4 с волновым сопротивлением Z_b2. Сопротивление Z_e2 рас­считывают так, чтобы входное сопротивление в схеме рис. 11.9, в по отношению к точкам а и Ь оказалось равным Z_B1 (при этом на линии с Z_B1 практически установится режим бегущей волны):

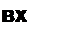
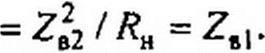R* cos90° -ь Z_b2 sin 90° cos 90°+ / ^-sin 90° Z_b2

Отсюда

На линии c Z_b2 есть и падающие, и отраженные волны.

Если нагрузочное сопротивление не чисто резистивное (Z_H - R_K + j .Y_H), то для согласования Z_bI с Z_H на заданной частоте к зажимам ab на рис. 11.9, в кроме четвертьволновой линии подключают еще отрезок короткозамкнутой линии, длину которой берут такой, чтобы суммарная входная проводимость четвертьволновой и дополни­тельной короткозамкнутой линий равнялась 1/Z_B1.

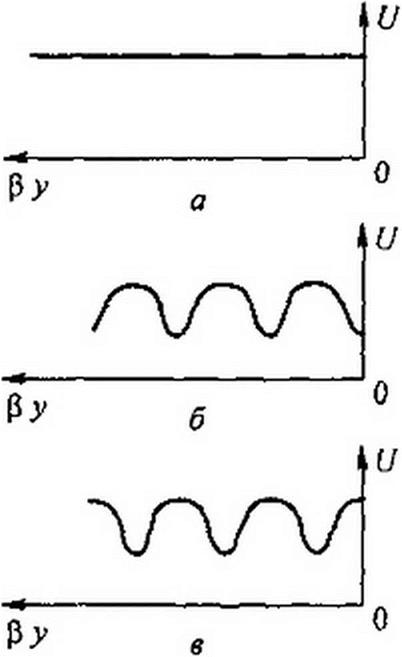
§ 11.25 Бегущие, стоячие и смешанные волны в линиях без по­терь. Коэффициенты бегущей и стоячей волн. При согласованной на­грузке на линии имеются только бегущие волны напряжения (U = U₂ e^{J ру}) и тока (/ = /₂ е^{у ру}). Так как при любом у |е^;ру | -1, то для бегущей волны действующее значение напряжения и тока вдоль ли­нии неизменно (рис. 11.10, а). При возникновении на линии стоячих волн
действующее значение напряжения на линии изменяется в функции расстояния у пропор­ционально {sin 0 yj при коротком замыкании (см. формулу (11.63)).

При несогласованной активной нагрузке на линии возникает смешанная волна — ком­бинация бегущей и стоячей волн. Если обо­значить т = Z_a/Z_H, то

О - 02 cos Р у + j m(j2 sin 0 у =

= cos0y + у(7₂ sin0y + jl/₂ (m-l)sin0y, или

(j - 02 е^{7 ₽ у} + j (т -1) (J₂ sin 0 у.

Первое слагаемое определяет бегущую, второе — стоячую волну.

Распределение напряжения на линии в функции расстояния у

U ~U₂ -'Iws² 0 у + w² sin² р у.

При т > I напряжение на конце линии минимально, а через четверть длины волны р у = л/2 максимально (рис. 11.10, б). При т<] напря­жение на конце линии максимально, а через 0у = я/2 минимально (рис. 11.10, в).

Коэффициентом бегущей волны называют отношение минимума на­пряжения смешанной волны к ее максимуму:

^б в

Коэффициент стоячей волны

*_св.=1/К_бв-

§ П.26. Аналогия между уравнениями линии с распределенными параметрами и уравнениями четырехполюсника. Напряжение и ток на входе линии с распределенными параметрами (1/_н/|) связаны с напряжением и током в конце этой линии (С/₂, /₇) следующими уравне­ниями (получены из (11.38) и (И.39), в которые вместо у подставлена длина всей линии /)•

U^U₂ chy/ + /₂ Z_B shy/;

А = ~ sh у / + /₂ ch у /.

Ли-» рь

Сопоставим их с известными уравнениями четырехполюсника:

~AU₂+B /₂;

ц ^c(j₂ + d!₂.

Из сопоставления следует, что уравнения по форме полностью ана­логичны, а если принять, что

/4 = Z) = chy/; (11.67)

£ = Z_Bshy/; (П.68)

C = shy//Z_B, (11.69)

то зависимость между й\ и 0₂, Ц ^и зависимость между /, и С/₂, /₂ в линиях с распределенными параметрами точно такие же, как и в четырехполюснике. Другими словами, при соблюдении условий (11.67)-(11.69) четырехполюсник эквивалентен линии с распределенны­ми параметрами в отношении связи между входными и выходными токами и напряжениями.

Напомним, что обратная постановка вопроса, т. е. запись уравнений четырехполюсника через гиперболические функции, рассматривалась в §4.11.

§ 11.27. Замена четырехполюсника эквивалентной ему линией с распределенными параметрами и обратная замена. При перемене местами источника и нагрузки в схеме (см. рис. 11.7) токи в источнике и нагрузке не изменятся. Таким же свойством обладает симметричный четырехполюсник. Поэтому однородная линия с распределенными пара­метрами может быть заменена симметричным четырехполюсником и, наоборот, симметричный четырехполюсник можно заменить участком однородной линии с распределенными параметрами. При замене будем исходить из уравнений (II .67)—(11.69) и зависимостей, с помощью кото­рых парахМетры симметричного четырехполюсника связаны с коэффи­циентами Л, В, С.

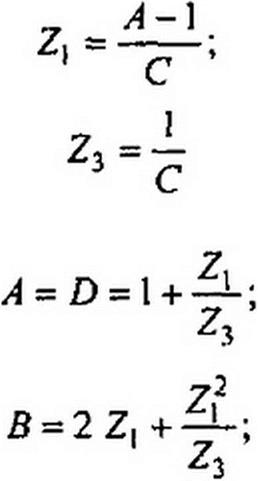Для симметричной Т-схемы замещения четырехполюсника

(11.70)

(И.71)

(11.72)

(11.73)

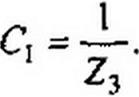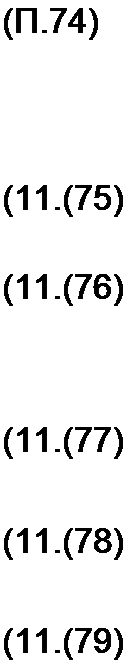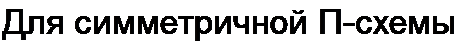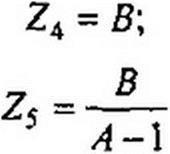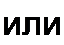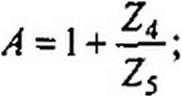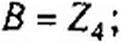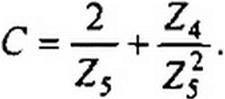Рассмотрим сначала последовательность операций при замене Т- и П-схем замещения четырехполюсника эквивалентной ему линией с распределенными параметрами (имеется в виду замена при фиксирован­ной частоте).

Пусть известны параметры Zj и Z₃ в Т-схеме (Z₄ и Z₅ в П-схеме). Требуется найти Z_B и у I для эквивалентной линии.

По формулам (11.72)—<11.74) или соответственно (11.77)—(11.79) на­ходим коэффициенты А, В, С.

Для определения волнового сопротивления Z_B разделим (11.68) на (11.69):

(11.80)

Для определения у/ составим выражение для th у/, использовав (11.67), (11.68) и (11.80):

_В_

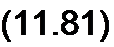/ sb У / V В /С гМс
th у / = —— « ,

ch у / А А

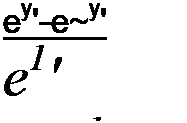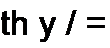Умножив и числитель, и знаменатель последней формулы на е’¹, получим

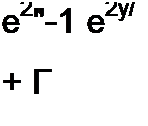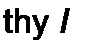Отсюда

_е2*/,_ег«_<елр> J + «^hY>\ (11.82)

I ~ th у у

Правую часть формулы (11.82) переведем в показательную форму. Пусть она будет равна М c^Jv. Тогда

е^2а/=М,

и так как

p/^v _ _P 7(v+2«*) _ */2 0/

V — V “* V У

где к — целое число, то

2 0/ -2 к л. у = V.

Отсюда

= | + (11.83)

Для реальных линий /?q, L_q, Cq, Gq >0. Это накладывает условие на определение к. Следует подсчитать р/ по приближенно известному значению фазовой скорости в линии

р/ = — (11.84)

и затем, сопоставив значения р/, найденные по (11.83) и (11.84), опре­делить А, округлив его значение до ближайшего целого числа.

Рассмотрим теперь последовательность операций при замене линии с распределенными параметрами эквивалентным ей четырехполюсником.

Известны у! и Z_B. Требуется найти сопротивления Z\ и Z₃ в Т-схе- ме (Z₄ и Z₅ в П-схеме). С зтой целью по (11.67)—(11.69) находим зна­чения коэффициентов А, В, С, а затем по (11.70) и (11.71) определяем Z; и Z₃ для Т-схемы (или по (11.75) и (11.76) — сопротивления Z₄ и Z₅ для П-схемы).

Возникает вопрос: любой ли симметричный четырехполюсник мож­но заменить участком линии с распределенными параметрами и любую ли линию с распределенными параметрами можно заменить четырехпо­люсником?

Очевидно, подобную замену можно осуществить, если полученные в результате расчета параметры таковы, что заменяющее устройство физически можно выполнить. Как правило, замена участка линии с рас­пределенными параметрами четырехполюсником возможна всегда, а обратная замена — не всегда. Она невозможна в тех случаях, когда в результате расчета волновое сопротивление окажется чисто мнимым чис­лом; в реальных линиях этого не бывает.

§ 11.28 Четырехполюсник'заданного затухания. Включаемый меж­ду источником сигнала и нагрузкой четырехполюсник, предназначенный для ослабления амплитуды сигнала а заданное число раз, называют че­тырехполюсником заданного затухания (аттенюатором). Его собирают обычно по симметричной Т- или П-схеме и нагружают согласованно.

Положим, что требуется найти сопротивления и Z₃ такого четы­рехполюсника, собранного по Т-схеме, полагая известными затухание а (в неперах) и характеристическое сопротивление Z_c. Исходим из двух соотношений:

ch а = I + — и Z_c = /BIC = Z_y + Z?.

?з

Из первого находим Z_} /Z₃ = ch а -1 и подставляем во второе.

Пример 118. Дано: а = 0.963 Нл; Z_c = 700 0m. Найти Zj и Zj.

Решение. Z,/Z₃ = ch0,963^<) -1 - 0,5; Z_{ = 0.5Z₃: Z_c=2.25Z_i; Z|=3I1Om;

Z₃ - 622 Ом.

§ 11.29 Цепная схема. На практике приходится встречаться со схе­мой, представляющей собой каскадное включение нескольких одинако­вых симметричных четырехполюсников (рис. 11.11).

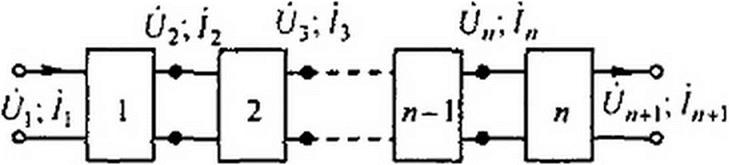Такую схему принято называть цепной. Исследование распределения тока и напряжения вдоль цепной схемы удобно проводить, используя теорию линий с распределенными параметрами. Действительно, в пре­дыдущем параграфе говорилось о замене одного четырехполюсника отрезком линии длиной /, имеющей постоянную распространения У и волновое сопротивление Z_B. Если число четырехполюсников равно п, то длина отрезка линии с распределенными параметрами будет в п раз боль- ,ше, т. е. равна nl.

Обозначим напряжение и ток на выходе п четырехполюсника через U,_I+i и /_п+|; тогда напряжение и ток на входе первого четырехполюсника

Ц ch у п I + /_w+l Z_B shy л/;

/i ₌!4±L_ch_Yn/ ₊ /_w+| z₈ chyn/.

’’Таблицу гиперболических функций см. в § 8.18.

Напряжение и ток на входе к от начала четырехполюсника {к < п):

U_k = ch(« - к +1) у Z + /_л+1 Z_B sh(n - к +1) у /; (11.87)

U 1

Ii = sh(n - к + 1) у / + I_rt+] Z_B ch(n - к +1) у I. (11.88)

Рассмотрим несколько числовых примеров на материал, изложенный в § 11.1-11.28.

Пример 119. Для некоторой линии длиной 5 км на частоте 1000 Гц были проведены опыты по определению ее входного сопротивления при холостом ходе и коротком замы­кании на конце линии. Оказалось, что Z_BXX = 535 е"⁷⁶⁴’Ом и Z_BXK = 467,5 e‘^7l0°. Тре­буется найти волновое сопротивление Z_B и постоянную распространения У этой линии.

Р е ш е я и е. Из формулы (11.53) следует, что при холостом ходе, когда Z₂ =« ^вх х = Z_B / thy /.

При коротком замыкании, когда Z₂ = 0,

^вх х ~ A thy А отсюда

Z, = Jz._{x х} Z_BXх = ^535е^-у64’ 467.5е"⁷'⁰° = 500 е“⁷³⁷° Ом; О У DA A DA А *

thy / = Vz„_x/z„, =0.935е'^зг.

По формуле (11.82),

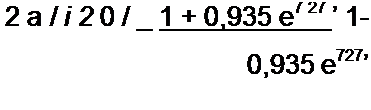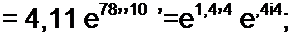4,11 = е^|,4М; 8140'= 1,414 рад;

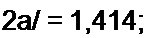а = 0,1414/(2/) = 0,1414; у = 0.2е'⁴⁵’км~‘; 0 = 0,1414.

Пример 120. Определить L$, G_o и С_о для линии примера 119, полагая Z_B = 500е~⁷³⁷° Ом и у = 0,2е^/45° км^-1.

Решение. В соответствии с формулами (И. 17) и (И. 19)

У Z_B = Rq+J<£>Lq.

Следовательно,

Ло + j о) L_o = 0,2 е^{7 45}“ 500 е“^{7 J7}° = 100е⁷⁸° = 99 + j 13,9,

или „ ₍

Л₀=99Ом/км и L_o =13.9/(2 л 1000) = 0,00222 Гн/км;

Таким образом,

G_o + у о> С_о = 0.2 е' ⁴⁵° / (500 е ^-7 ) = 0,05 57 • 10'^J + у 0,369 • 10‘³.

Пример 121, Линия примера 120 подключена к постоянному напряжению (<о = 0). Определить напряжение и ток в начале линии, если на конце линии включена нагрузка 300 Ом и ток в нагрузке 0,5 А.

Решение. По формуле (11.25) находим волновое сопротивление линии Z* для по* стояиного тока:

Z, = V99/0,0557-10’³ = 1330 Ом.

Постоянная распространения (см. формулу (11.20))

У = 7*о Go = 799 0,0557-10^-3 = 0,0743 км"¹.

По формулам (11.38) и (1J .39), при у « I

U_{ =U₂ chy/ + /₂ Z_B shy/; /| = /₂ chy/ + —shy /.

По условию /₂=0,5А; U₂ = /₂ /?₂ = 0,5-400 = 200 В; у / = а / = 0.0743-5 = 0,371; ch а / = ch0,371 = 1.07; sha/ = sh 0,371 =0,379. Следовательно,

L/| = 200 • 1,07 + 0,5-1330 • 0,379 = 466 В;

/, = 0,5 • 1,07 + — • 0.379 = 0.694 А.

1330

Пример 122. Линия примера 119 короткозамкнута на конце и присоединена к источ­нику синусоидального напряжения частотой 1000 Гц. Определить напряжение и ток в начале линии, если ток в конце линии /_г = 1 А.

Решение. При коротком замыкании

U_t =/₂ Z^$hy Г, i_}=i₂Z,chyl.

По данным примера 119,

у = a + y p = 0,1414 + j 0,1414км’¹; /=5км;

у / = 0.707 + j 0.707;

_С У! _{= е}0.707 _еу 0.707 _{= 202 (CQS 40} о₂₀- ₊ j _{sjn 4}qo₂o’) = j,54 + j 1.305;

e"^Y' _=e -0.707 _e- /0.707 _ ₀ 495 (cos40°20'- j sin40°20') = 0.377- j0,32;

chy / = 0.5 (e^y/ + e*^Y/) = 0.96 + j 0.4925 = 1,07 ^2Г20‘-

г_в=500е"^/ЗГОм;

sh у / = 0.5 {e^y/ - e"-') = 0,582 + j 0.812 * e' ⁵⁴’²⁰'.

Следовательно,

(/ = /₂ Z_B sh у / = 1 ■ 500 e’^{7 3r 54}’²⁰' = 500 e^7,7‘²⁰' B;

A =/₂ chy/= 1.07 e'²⁷*²⁰’ A.

Пример 123. Линия примера 119 замкнута на активное сопротивление Z₂ =400 Ом.

Определить U_t и /_ь если по нагрузке протекает ток /₂=О.5А; / = 1000 Гц. Решение.

Ц = U₂ ch у / + /₂ Z_B sh у / = 200 • 1,07 е^{7 2Г20}‘ + 0.5 • 500 е’^{7 37}° е^{7 54}°²⁰' = 463 е' ^2Г В;

/] = /₂ ch у / +-^ sh у / = 0,8 е^{7 $3}°³⁸ А.

^В

Пример 124, По данным примера 123 определить комплекс действующего значения падающей волны в начале линии (А,).

Решение. В соответствии с формулой (11.31)

_А -_{А е}7Ф.^1 ⁺ Аг_в_ 463е^^2а₊0,8с'^53в58'500е->^ ^{2 2} 2 2

Пример 125. Записать выражение для мгновенного значения падаюшей волны налря- жения в начале и конце линии по данным примера 124.

Решение. Мгновенное значение падаюшей волны напряжения в начале линии при х = 0

V2-431sin(o/4-19°30').

Мгновенное значение падающей волны напряжения в конце линии при х = / в общем виде

V? А₂ e^-ot' sin(ci)г + ч/_п - р /); определяем

_е -а/ _{= е}-о.ТО7 _{= 0}д₉₅.

Р t = 0,707 рад = 40°20';

VI А₂ е"^а/ = 41 431 -0.495 = 301 В;

ц/_п - р I = 19°31' - 40°20' = -20°50'.

Следовательно, мгновенное значение падаюшей волны напряжения а конце линии 301 sin(o t - 20°50') В.

Пример 126. Определить затухание в неперах для линии примера 119, если на конце ее включена согласованная нагрузка.

Решение. Затухание в неперах равно а.

Так как произведение а I = 0,1414-5 = 0.707. то затухание линии равно 0,707 Ни.

Пример 127. Какую дополнительную индуктивность /-одап нужно включить на каж­дом километре телефонной линии с параметрами: Я₀=ЗОм/км; L_o = 2■ Ю^-3Гн/км; С_о = Ю^Ом-км”¹; Cq = 610'⁹Ф/км, чтобы линия стала неискажающей?

Решение. Для того чтобы линия была неискажаюшей, ее параметры должны удов­летворять уравнению (11.46). Следовательно.

4₀ -с + £о = -^-^- = 3-6-10'⁹/10‘⁶ = 18 10’⁵Гн/км; V M\z II w

о₀

^Одоп = 18 - 2 = 16 мГ /км;

Пример 128. Определить наименьшую длину короткозамкнутой на конце двухпровод­ной воздушной линии, чтобы при частоте 10* Гц входное сопротивление ее равнялось 800 у Ом. Расстояние между осями проводов «У = 20 см, радиус каждого провода г = 2 мм.

Решение. В соответствии с формулой (11.57)

Z_BKK= j \ILq/С_о igp у.

Для двухпроводной линии

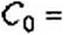Lq Ро/НЛ/лН² /17^

Q Cq \ К ) ’ll C_o К j Eq

^ = 3770m; .[A = 377 1A22/A = 553 Qm.

£q V Cq ^я

По условию 800 y = у 553 tg Ру. Отсюда

tgP у = 800/553= 1,445;

Р у = 55°20' = 0,963 рад;

Р = <•> -Jl_q С_о = 2,09-10^-2 см^-1.

Искомая длина линии

у = 0,963 /(2,092 ■ 10’²) = 46,1 см.

Пример 129. В Т-схеме рис. 4.4, a Z_t =100 Ом, Z₃ =-500 у Ом. Определить харак­теристическое сопротивление четырехполюсника и произведение yl эквивалентной ему линии с распределенными параметрами.

Решение. В соответствии с формулами (11.72)—(11.74)

х = I ₊ А ₌ j ₊ —¹⁰⁰ = I + о,2 у = 1,02 е■' ’^|С|8';
Z₃ - 500 у

у 2 1 г\4

В = 2Z, + =±- = 200+ —— = 200 + 20 у = 200е'™ \

¹ Z₃ -500у

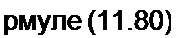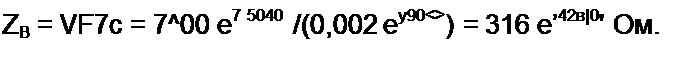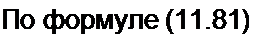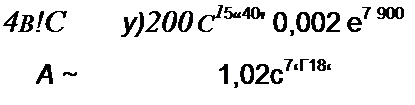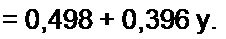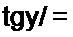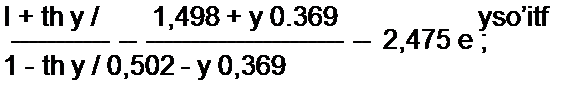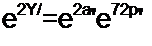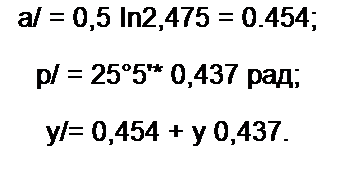яснитс переход от уравнений для мгновенных значений и и i уравнений (11.1) и (11.4) к уравнениям для комплексных значений (j и / (уравнениям (11.7) и (11.8)). 4. Каков фи­зический смысл постоянной распространения у и волнового сопротивления Z, ? 5. Если два провода двухпроводной линии с малыми потерями раздвинуть по сравнению с их исходным состоянием, то как это скажется на Z, и у? 6. Как определить Z_g и У опыт­ным путем? 7. Из каких условий определяют постоянные и Л₂? 8. Как показать, что сигнал, проходя по линии без искажений, не изменяет своей формы? 9. Почему в линии передачи информации стремятся брать Z_H =Z_e? 10. Линия без потерь нагружена несо­гласованно. Коэффициент отражения по напряжению к_и =1/3. Чему равно Z„ в долях от Z_B? 11. В чем различие между бегущей и стоячей волнами в физическом и математи­ческом отношениях? Какую волну называют смешанной? 12. Покажите, что линия без по­терь является неискажающей. 13. При каком соотношении между параметрами можно считать реальную линию с /?₀#0 и <7₀*0 как линию без потерь? 14. Линия длиной А/2 напружена согласованно, у = 0,1 + 0,314 j. Определите КПД линии. (Ответ: 0,133.) 15. Ли­ния имеет длину 10 км и у = 0,2+ 0,314 у. В середине линии (7_П = ЮОе⁷³⁰* В, 6_отр= 50е"'³⁰ В. Запишите мгновенные значения и_п и и₀ в начале линий. (От­вет: и_п-222 sin(<o / +120°), «о ~ 36,8 siп(ш t -120°).) 16. В каком смысле четырехполюсник может быть эквивалентен линии с распределенными параметрами? 17. Как рассчитать элементы аттенюатора по известным а и Z_e? 18. Каково назначение четвертьволнового трансформатора? 19. Решите задачи 13.3; 13.11; 13.23; 13.31; 13.37; 13.43.

Глава двенадцатая

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ,