С распределенными параметрами
§ ПЛ. Основные определения. В данной главе рассмотрены основы теории установившихся процессов в электрических цепях, содержащих линии с распределенными параметрами.
Электрическими линиями с распределенными параметрами называют такие линии, в которых для одного и того же момента времени ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) линии к соседней точке, т. е. являются функциями времени и пространственной координаты.
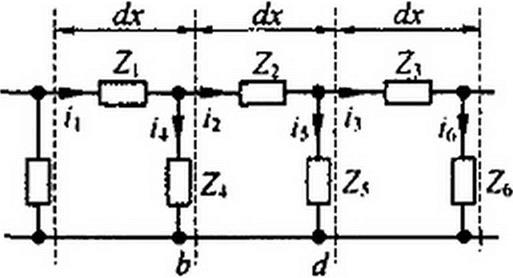
Эффект непрерывного изменения тока и электрического напряжения вдоль линии имеет место вследствие того, что линии обладают распределенными в пространстве продольными и поперечными элементами (рис. 11.1, а).
На рис. 11.1, а изображен участок линии с распределенными параметрами, через dx обозначен бесконечно малый элемент длины линии.
Сопротивления ZlfZ2,Z3,... называют продольными, в них включены сопротивления прямого и обратного проводов; сопротивления Z4, Z5, Z6,... называют поперечными.
В результате утечки тока через сопротивление Z4 ток /2 Аналогично, ток /3 * i2 и т. д. Напряжение между точками а и b не равно напряжению между точками с и d и т. д.
 | |||||
 | |||||
 | |||||
|
Рис. П.1
В электрических линиях с распределенными параметрами продольные сопротивления образованы активными сопротивлениями проводов линии и индуктивностями двух противостоящих Друг Другу участков линии длиной dx. Поперечные сопротивления состоят из сопротивлений утечки, появляющейся вследствие несовершенства изоляции между проводами линии, и емкостей, образованных противостоящими друг другу элементами (участками) линии.
Линию с распределенными параметрами называют однородной, если равны друг другу все продольные сопротивления участков линии одинаковой длины и равны друг другу все поперечные сопротивления участков линии одинаковой длины. Участок линии на рис. 11.1, а однороден, если Z, = Z2 = Z3 =... и Z4 - Zs = Z6 -....
Линию с распределенными параметрами называют неоднородной, если продольные сопротивления в ней различны или поперечные сопротивления неодинаковы.
Кроме того, линии с распределенными параметрами можно подразделить на две большие группы: нелинейные и линейные. В нелинейных линиях с распределенными параметрами продольные и (или) поперечные сопротивления являются функциями протекающих по ним токов, в линейных продольные и поперечные сопротивления не являются функциями протекающих через них токов.
Кроме электрических диний с распределенными параметрами существуют и магнитные линии с распределенными параметрами. Под магнитными линиями с распределенными параметрами понимают такие линии, магнитный поток и магнитное напряжение вдоль которых непрерывно меняются при переходе от одной точки линии к соседней (см. § 14.24).
В магнитных линиях с распределенными параметрами продольные сопротивления представляют собой магнитные сопротивления самих магнитных стержней, образующих магнитную линию, а поперечные сопротивления обусловлены утечкой магнитного потока по воздуху между противостоящими друг другу участками линии.
Примером нелинейной электрической линии с распределенными параметрами является электрическая линия передачи высокого напряжения при наличии между проводами линии тихого электрического разряда (явление короны на проводах). В этом случае емкость между противостоящими друг другу участками линии является функцией напряжения между этими участками.
Примером нелинейной магнитной линии с распределенными параметрами является линия, образованная параллельно расположенными магнитными сердечниками, которые в процессе работы линии могут насыщаться.
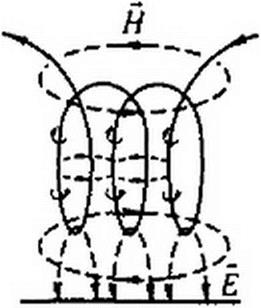
Когда используют термин «линия с распределенными параметрами», то обычно его мысленно связывают с мощными линиями передачи электрической энергии на большие расстояния, с телефонными и телеграфными воздушными и кабельными линиями, с рельсовыми линиями автоблокировки на железнодорожном транспорте, с антеннами в радиотехнике и другими родственными линиями и установками. В то же время с линиями с распределенными параметрами имеют дело, когда «линий» в буквальном смысле слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка при достаточно высоких частотах представляет собой линию с распределенными параметрами. Картина электрического и магнитного полей катушки показана на рис. 11.1, б. Ливии напряженности электрического поля £ показаны штриховой линией, линии напряженности магнитного поля Н — сплошными линиями.
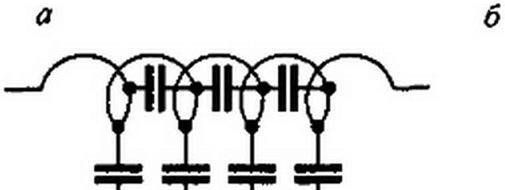
Схема замещения катушки показана на рис. П.1, в. Из рисунка видно, что кроме индуктивностей в схеме есть межвитковые емкости и емкости на корпус прибора (на землю). Если по катушке проходит переменный ток, то через межвитковые емкости и емкости на землю также идет ток. При одном и том же напряжении между соседними витками ток через емкости тем больше, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости несоизмеримо мал по сравнению с токами через витки катушки и наличие емкостей можно не учитывать в расчете (что и делалось до сих пор). Если же частота тока очень велика, например сотни миллиардов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление (количественные изменения перешли в качественные). При промежуточных частотах порядка нескольких мегагерц (когда линейные размеры катушки соизмеримы с длиной волны) индуктивная катушка является типичной линией с распределенными параметрами. Если индуктивная катушка намотана на стальной сердечник, который способен насыщаться, и частота тока достаточно велика, то все устройство в целом представляет собой сложную совокупность из электрической и магнитной нелинейных цепей с распределенными параметрами.
В главе 11 рассмотрены основы однородных линейных цепей с распределенными параметрами. Вся теория излагается применительно к электрическим линиям с распределенными параметрами на переменном •токе. Теория однородных линейных электрических цепей с распределенными параметрами на постоянном токе непосредственно следует из теории цепей переменного тока, если принять угловую частоту равной нулю.
Теория однородных линейных магнитных линий на постоянном токе в значительной мере аналогична теории однородных линейных электрических линий с распределенными параметрами, только вместо тока в уравнении должен быть подставлен магнитный поток, электрическое напряжение заменено магнитным напряжением, продольное активное сопротивление — продольным магнитным сопротивлением, поперечная электрическая проводимость — поперечной магнитной проводимостью (см. главу 14). Теория магнитных линий с распределенными параметрами на переменном токе рассмотрена во втором томе учебника, г
§ 11.2 Составление дифференциальных уравнений для однородной линии с распределенными параметрами. Пусть — продольное активное сопротивление единицы длины линии; До — индуктивность
 |
|
единицы длины линии; Со — емкость единицы длины линии; GQ — поперечная проводимость единицы длины линии. Поперечная проводимость Go не является обратной величиной продольного сопротивления Rq.
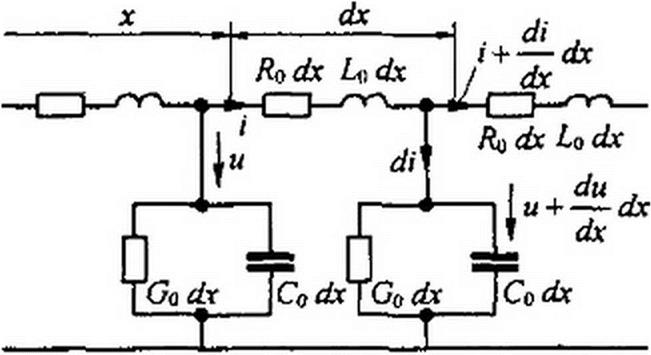
Разобьем линию на участки длиной dx (рис. И.2), гдех — расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно /?о dx, индуктивность — Ло dx, проводимость утечки — Gq dx. Обозначим ток в начале рассматриваемого участка линии через /, а напряжение между проводами линии — через и. И ток, и напряжение являются в общем случае функциями расстояния вдоль линии х и времени t. Поэтому в дальнейшем в уравнениях использованы частные производные от и и i по времени / и расстоянию х.
Если для некоторого момента времени t ток в начале рассматриваемого участка равен I, то в результате утечки через поперечный элемент ток в конце участка для того же момента времени равен i +— dx, где дх dil дх — скорость изменения тока в направлении х. Скорость, умноженная на расстояние dx, является приращением тока на пути dx.
Аналогично, если напряжение в начале участка и, то в конце участка
ди , для того же момента времени напряжение равно и + — dx.
дх
Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке:
После упрощения и деления уравнения на dx получим
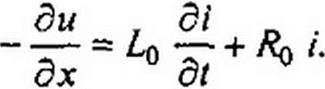 | |||||||
 | |||||||
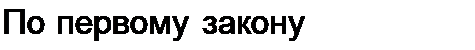 | |||||||
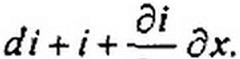 | |||||||
Ток di (см. рис. 11.2) равен сумме токов, проходящих через проводимость Gq dx и емкость Со dx:
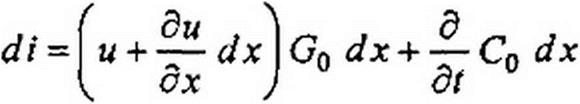 | |||
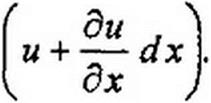 |
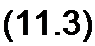 Пренебрегаем слагаемыми второго порядка малости. Тогда
Пренебрегаем слагаемыми второго порядка малости. Тогда
di = и Gq dx + C0 dx —.
dl
Подставим (11.3) в (11.2), упростим и поделим уравнение на dx:
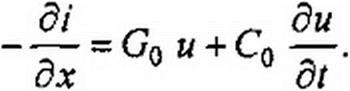 | |||
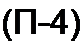 | |||
Уравнения (11.1) и (11.4) являются основными дифференциальными уравнениями для линии с распределенными параметрами.
§ 11.3 Решение уравнений линии с распределенными параметрами при установившемся синусоидальном процессе. Пусть напряжение и ток в линии изменяются по синусоидальному закону во времени. Воспользуемся символическим методом.
Изображение тока
i = In, sin(« I + <р,) -> i ,
где / = еу Ф1 /41.
Изображение напряжения
u = Um sin(co Г ч- <р„) —> С/ е7
где U = Um е7 / Л..
Комплексы U и / являются функциями расстояния х, но не являются функциями времени. Множитель е7“' есть функция времени /, не зависящая от х.
Представление изображений тока и напряжения в виде произведения двух множителей, из которых один является функцией только х, а другой — функцией только /, дает возможность перейти от уравнений в частных производных (уравнений (11.1) и (11.4)) к уравнениям в простых производных. Действительно,
дх дх ’
dt dt
| dx dx' Ca~^Ju>C0()eJ,“ ot |
| (11.6) |
| Подставим (11.5) и (11.6) в (11.1) и (11.4), сократив в полученных уравнениях множитель е;ыГ: |
| где |
| (И.7) (И.8) (П.9) (H-Ю) |
| Решим систему уравнений (11.7) и (11.8) относительно U. С этой целью продифференцируем (11.7) по х: |
| dl dx* dx |
| (И.Н) |
| В (11.11) вместо dl / dx подставим правую часть уравнения (11.8): |
| ^- = Zoroy. (11.12) dx Уравнение (11.12) представляет собой линейное дифференциальное уравнение второго порядка. Его решение |
| еуЛ +А2 |
| (11.13) |
| Комплексные числа А} и Д есть постоянные интегрирования, которые в дальнейшем определим через напряжение и ток в начале или через напряжение и ток в конце линии. Комплексное число |
| (11.14) |
| называют постоянной распространения; его можно представить в виде |
| У = а + У Р, |
| (И.15) |
| где а — коэффициент затухания, характеризующий затухание падающей волны на единицу длины линий, например на 1 м (км); р— коэффици- |
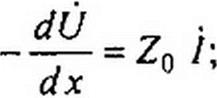
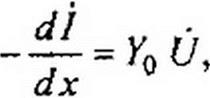
ент фазы, характеризующий изменение фазы падающей волны на единицу длины линии, например на 1 м (км). Следовательно,
[У1 = [а] = [р] = 1/м.
Ток I найдем из уравнения (11.7):
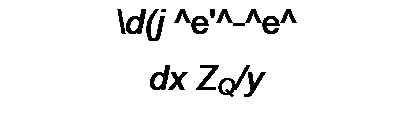 | |||
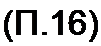 | |||
Отношение ZQ/y = Zo/*o = лМо /^о» имеющее размерность со
противления, обозначают ZB и называют волновым сопротивлением:
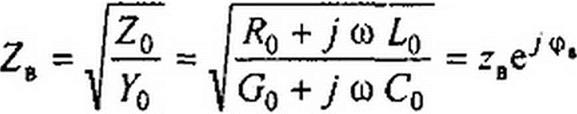 | |||
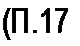 | |||
где zB—модуль; <рв—аргумент волнового сопротивления ZB. Следовательно, « 4
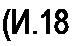 /=Ае'тх-Ает\
/=Ае'тх-Ает\
Z Z
§ 11.4 Постоянная распространения и волновое сопротивление. Как указывалось ранее, постоянная распространения
у - а + / р = J со £о) (Со + / со Со). (11.19)
Для линии постоянного тока СО=;0 и потому
Y = 7«oGo. (11.20)
Для линии синусоидального тока без потерь (Яо = Gq ~ 0)
у = j со -JRq Cq. (11.21)
Запишем формулы для приближенного определения Р и а в линии с малыми лоте рями, когда RqI& Lq «1 и Go/coCo « I. С этой целью перепишем формулу (11.19) еле дующим образом:
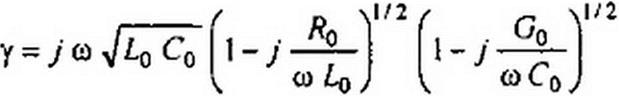 |
и разложим биномы в ряды, ограничившись двумя членами каждого ряда (т. е. воспользу емся соотношением VI + х «1 + 0,5 х ). В результате получим
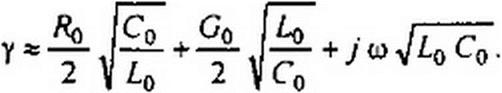 | |||||||
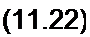 | |||||||
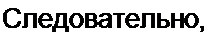 | |||||||
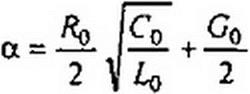 | |||||||
|
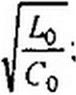 | |||
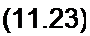 | |||
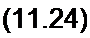 | |||
Рассмотрим вопрос о волновом сопротивлении. Для постоянного тока (о = 0) из (11.17) следует, что
Z„ = А^о- (11.25)
Для линии синусоидального тока без потерь (Rq = Go = 0)
Z^L^C*. (11.26)
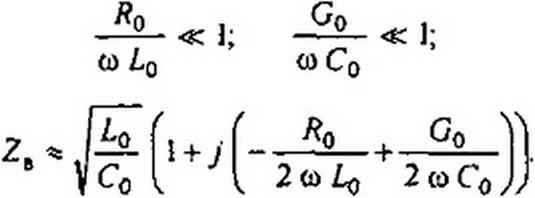 |
|
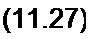 |
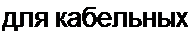 Для реальных воздушных линий |Ze |~ 300+ 600 Ом, ]ZJ «в 50 + 200 Ом. Угол Ф имеет емкостный характер.
Для реальных воздушных линий |Ze |~ 300+ 600 Ом, ]ZJ «в 50 + 200 Ом. Угол Ф имеет емкостный характер.
§ 11.5 Формулы для определения комплексов напряжения и тока в любой точке линии через комплексы напряжения и тока в начале линии. Как и раньше, через х будем обозначать расстояние от начала линии до текущей точки на ней. Пусть в начале линии при х - 0 напряжение {7| и ток Составим уравнения для определения постоянных Л, и А2 через и Д. Из (11.13) и (11.18) следует (х = 0):
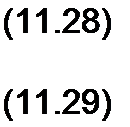 Ц = а2 + а}-
Ц = а2 + а}-
~ А2 ~ А-
Для определения из (11.28) вычтем (11.29):
4 =0,5 (Ц A ZJ = Ai (11.30)
А=0,5(Ц+/17в)=/12е-/ч/", (11.31)
где А}—модуль; у0— аргумент комплекса Д; А2—модуль; ц/п — аргумент** комплекса А2.
Подставим (11.30) и (11.31) в (11.13):
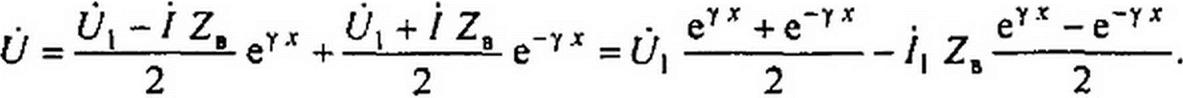 |
Введем гиперболические функции. Известно, что
chx = 0,5 (ех + е“х), shx = 0,5 (ех -е-х).
Индексы «о» и «п» — начальные буквы слов «отраженная» и «падающая» волны (см. § 11.8).
 | |||||||||||||||
 | |||||||||||||||
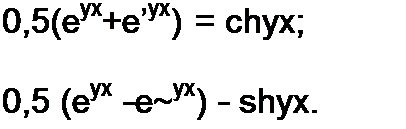 | |||||||||||||||
 | |||||||||||||||
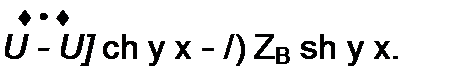 | |||||||||||||||
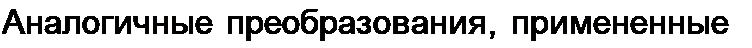 | |||||||||||||||
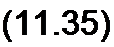 | |||||||||||||||
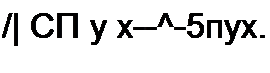 | |||||||||||||||
Формулы (11.34) и (11.35) позволяют найти комплексы напряжения и тока в точке линии, расположенной на расстоянии х от ее начала. Следует иметь в виду, что аргументом гиперболических функций в этих формулах является комплексное число у х = а х + j Р х.
§ 11.6 Графическая интерпретация гиперболических синуса и косинуса от комплексного аргумента. Гиперболические функции от комплексного аргумента сами являются комплексами и могут быть изображены векторами на комплексной плоскости.
Заменим ух в уравнениях (11.32) и (11.33) на aх + урх:
chYx = |(eaV,!j'+e-‘"e-'|ix);
shrz = l(e“V₽',-e-“'e-j|!l).
По таблицам показательных функций найдем значение еах и е-ах и на комплексной плоскости (рис. 11.3) отложим векторы еахеурх и е~ахе"-/ $х. Первый из них по модулю равен еах и относительно оси действительных значений повернут на угол р х против часовой стрелки; второй по модулю е"а х и относительно оси действительных значений повернут на угол Р х по часовой стрелке.
| Рис. п.з |
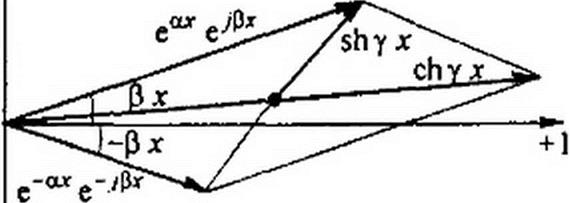
| Гиперболический косинус равен полусумме этих векторов, а гиперболический синус — их полуразности. |
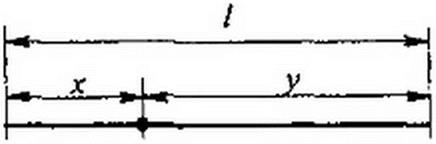
| § 11.7. Формулы для определения напряжения и тока в любой точке линии через комплексы напряжения и тока в конце линии. Обозначим расстояние от текущей точки на линии до конца линии у, а длину всей линии (рис. 11.4) Г. |
| (11.36) |
| начало |
| Рис. 11.4 |
| линии |
| конец |
| Пусть известны напряжение и ток в конце линии (Л и /2. Подставим х = 7, 4/=6'2, / = /2 в (11.13) и (11.18) и составим два уравнения для определения постоянных интегрирования А} и Д21 |
| 4/2 = Л e~v/ + Л eY/> |
| Л Z„ = e",z - Л, еу1. |
| Отсюда |
| Л, = 0,5 (1>2 -/2 Z.) е"" = А, е' Л2 = 0,5 (У2 +/2 Z,)e-" = A2eJv’. |
| (11-37) |
| Если подставить (11.37) в (11.13) и (11.18), заменить 1-х на у и перейти к гиперболическим функциям, то получим |
| U = U2 chyy + /2 ZB shy у; |
| (11.38) |
| shy у + /2 ZB chyy. |
| (11.39) |
| Зная U2 и с помощью формул (11.38) и (11.39), можно найти комплексы напряжения и тока в точке, находящейся на расстоянии у от конца линии. |
| § 11.8. Падающие и отраженные волны в линии. Подставим в формулу (11.13) j] е74'0 вместо Л,, А2 е7Ч,п вместо А2 (см. (11.34)), заменив У на а + ур, получим |
| U = AX + А2 e’axe7(v”‘Px) |
| (11.40) |
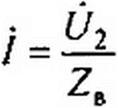
Аналогичную операцию проделаем с формулой (11.18), причем в дополнение заменим ZB на zB еУ Ф" (см. формулу (11.17)):
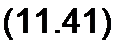 4. A <»*p/(Ve+px-4>.) ■ ^2 р-алг 7(^л-р.г-ф«)
4. A <»*p/(Ve+px-4>.) ■ ^2 р-алг 7(^л-р.г-ф«)
Для перехода от комплексов напряжения и тока к функциям времени умножим правые части формул (11.37) и (11.38) на V2 eyw/ и от произведений возьмем мнимую часть:
и~ At V2earsin jfat + у0 + 0х) + Л2 V2e"a ' sin + -₽х); (11.42)
(11.43)
е arsin(tof + ц/п-рх-ч>в).
Падающей электромагнитной волной называют процесс перемещения электромагнитного состояния (электромагнитной волны) от источника энергии к приемнику, т. е. в нашем случае в направлении увеличения координаты х. Электромагнитное состояние определяется совокупностью электрического и магнитного полей, обусловливающих друг друга. Падающая волна, распространяясь от источника энергии к приемнику, несет энергию, заключенную в ее электрическом и магнитном полях.
Отраженной электромагнитной волной называют процесс перемещения электромагнитного состояния (электромагнитной волны) от приемника к источнику энергии, т. е. в нашем случае в сторону уменьшения координаты х.
Падающая электромагнитная волна образована падающей волной напряжения (второе слагаемое формулы (11.42)) и падающей волной тока (второе слагаемое формулы (11.43)). Отраженная электромагнитная волна образована отраженной волной напряжения (первое слагаемое формулы (11.42)) и отраженной волной тока (первое слагаемое формулы (Н.43)).
Знак минус отраженной волны тока свидетельствует о том, что поток энергии, который несет с собой отраженная электромагнитная волна, движется в обратном направлении по сравнению с потоком энергии, который несет с собой падающая волна.
Каждая компонента падающей волны (волны напряжения или волны тока) представляет собой синусоидальное колебание, амплитуда которого уменьшается по мере роста х (множитель е”и т), а аргумент является функцией времени и координаты х.
Каждая компонента отраженной электромагнитной волны затухает по мере продвижения волны от конца линии к началу (множитель e01"*).
Физически эффект уменьшения амплитуд падающей и отраженной волн по мере их продвижения по линии объясняется наличием потерь в линии.
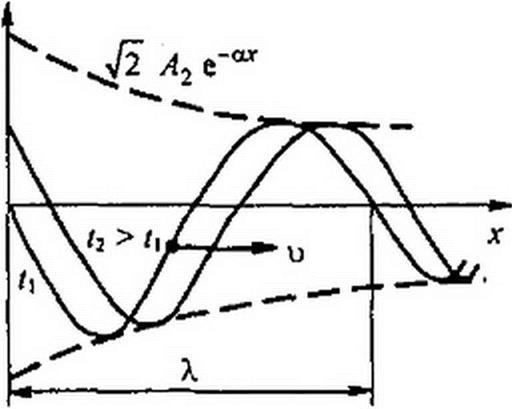
На рис. П.5 изображены графики распределения падающей волны напряжения вдоль линии (в функции х) для двух смежных моментов времени: Г) и t2 >/Р Падающая волна распространяется слева направо. При построении принято й)/5 +уп -0.
 |
|
 |
|
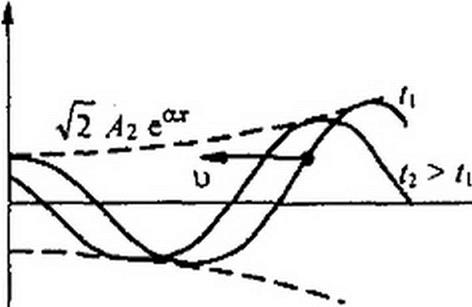
На рис. 11.6 представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: 6 и t2 >t\. Отраженная волна распространяется справа налево.
§ 11.9 Коэффициент отражения. Отношение напряжения отражен ной волны в конце линии к напряжению падающей волны в конце линии
называют коэффициентом отражения по напряжению и обозначают Ки. В соответствии с формулой (11.40)
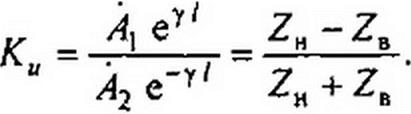 |
При согласованной нагрузке Ки=0, при холостом ходе Ки=1. Коэффициент отражения по току К, - -Ки.
§ 11.10 Фазовая скорость. Фазовой скоростью 4$ называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость — это скорость перемещения по линии неизменного фазового состояния. Если фаза падающей волны напряжения неизменна, то в соответствии с формулой (11.42)
со t + “0 х - const.
Возьмем производную по времени от обеих частей последнего равенства:
— (со I + ц/п - р х) = 0, или со - Р ~ - 0.
dt dt
Отсюда
dx (а
Уд, = '— = —1
ф dt р
Пример 116. Найти фазовую скорость для воздушной двухпроводной линии с малыми потерями.
Ре ше н ие. Из формулы (11.24) следует, что 0 - со у /Lq Со. Поэтому
Индуктивность единицы длины двухпроводной воздушной линии
Lowin', п г
где Мо — магнитная постоянная: d— расстояние между осями проводов; г — радиус каждого провода.
Емкость единицы длины воздушной двухпроводной линии [I]:
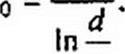 |
|
где £0 — электрическая постоянная. Фазовая скорость
Оф = — ~ 300000 км / с.
VI,256 • i О’6 Гн /с • 8.86 • 1 О’12 Ф /м
§ 11.11 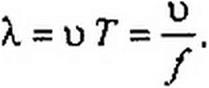 Длина волны. Под длиной волны X понимают расстояние, на которое распространяется волна за один период Т = 1//:
Длина волны. Под длиной волны X понимают расстояние, на которое распространяется волна за один период Т = 1//:
(11.45)
Пример 1(7. Найти длину электромагнитной волны при / = 50 и 50-(О6 Гц.
п ГТ г сл г- 1 300000км/с л
Решение. При/= 50 Гц X = •--------------------------- ;------ = 6000 км.
50с‘
При f = 50 IО6 Гц Х = 6м.








