Z|(p)-p £| -р3 £, + Р2 £,) + р^-Ьц Д]) + а0

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Обратим внимание на то, что в знаменателе Уо(р) имеется слагаемое - р³ кото­рое при дальнейшей реализации приведет к появлению в схеме отрицательной индуктив­ности.

8. Поскольку при p = j W] Z_}(р) - р = 0, то У₀(р) = а>, т. е. p = jti>o является по­люсом К₀(р). Наличие полюса у Y_Q{p) позволяет представить оставшуюся часть двух­полюсника ветвью из последовательно соединенных £, и С₂, настроенной в резонанс на частоту <о₀, и параллельно ей присоединенного двухполюсника сопротивлением Z₂(/?) (рис. 10.5, г):

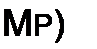(10.8)

9. Полагают Z₂(p)= W₂(p)/M₂(p). Степени полиномов ^2(^>) и М₂(р) должны быть такими, чтобы после приведения правой части (10.8) к общему знаменателю степень полинома числителя левой части равнялась степени полинома числителя правой части; то же и в отношении степеней знаменателей. Так. если Х₀(р) соответствует выражению (10.7), то Z₂(p) = Л'₂(р)/Л/₂(р).

Методом неопределенных коэффициентов можно найти с^, d_Q и Ь₂. В рассмат­риваемом случае

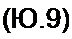ci — — £| coj; Cq = gq, do = Z>q,

L₂ = Д) /(b_Q - «5); c₂ = 1 /(<0q L₂).

Разность (д_о-соб)>О; это следует из того, что условие ^,>0 означает, что

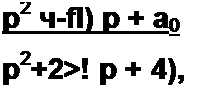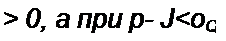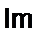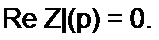10. Реализацию Z₂(p) производят, как правило, лестничной схемой. В рассматрива­емом примере Z₂(p) реализуют индуктивным (£₃ = с_|/г/₀ = -<оо Д|/6₀) ^и резистивным (Я₃ = а₀ fb_Q) элементами (рис. 10.5, о). Важно обратить внимание на то, что Lj оказалась отрицательной.

11. Так как физически осуществить отрицательную Ly в линейной цепи невозможно, то дальнейший этап реализации в методе Бруне состоит в том, чтобы три магнитно не связанные индуктивные катушки, имеющие индуктивности £₄, £₅ и £₃, заменяют транс-

форматором, состоящим из двух катушек— L₄ и L_s, между которыми имеется магнит­ная связь (взаимная индуктивность М). Это действие является обратным по отношению к операции «развязывания» магнитно-связанных цепей.

На рис. 10.5, е изображены два участка цели: левый —до преобразования, правый — после преобразования; показаны положительные направления токов в ветвях и указаны одноименные зажимы катушек.

Напряжения между точками / и 2 для обоих участков цепи в силу их эквивалентнос­ти должны быть одинаковы, т. е.

р £| /\ + р Ь₂ /₂ = р £₄ Д - р М /₃;

—р L₂ /₂ + Р Т-з Iз ~ Р 7₃ — р М I).

Подставляя в эти две строки /, = /₂ + /₃ и учитывая, что каждая из них должна удов­летворяться при любых значениях токов, получают

£4 £i + £₂; £5 = £3 + £3,

где L₄ и £5 положительны. Окончательная схема изображена на рис. 10.5, ж.

12. Если условиться сумму степеней полиномов в числителе и знаменателе ^мд(р) называть порядком Z^(p), то совокупность перечисленных операций («цикл Бруне») позволяет снизить порядок на четыре. Естественно, что потребность в каком-либо одном или нескольких этапах в любом конкретном примере может и не возникнуть (например, в этапах 1 или 3).

Для Z^p), порядок которых достаточно высок, может возникнуть потребность при­менить эту последовательность операций не один раз. В заключение отметим, что если в п. 5 A'i <0, то £_t <0, а вычитание, согласно п. 7, сопротивления -р|£| j сводится к прибавлению сопротивления +р | |.

Некоторым недостатком метода Бруне является его относительная сложность и необ­ходимость введения в схему идеального трансформатора с коэффициентом связи k² =M²/{L₄ £,) = ].

§ 10.6 Понятнее минимально-фазовом и неминимально-фазовом четырехполюсниках. У минимально-фазовых (м. ф.) четырехполюсни­ков все нули передаточной функции расположены в левой части плоско­сти /?. У неминимально-фазовых (н. ф.) четырехполюсников хотя бы часть нулей находится в правой части плоскости р.

Название объясняется тем, что при одинаковом значении модулей передаточной функции м, ф, и н. ф. четырехполюсников аргумент пере­даточной функции м. ф. четырехполюсника меньше аргумента передаточ­ной функции н. ф. четырехполюсника. Поясним сказанное.

Сравним выражения для двух передаточных функций:

_и К\р) = ^{Р Р[}-. р-р₂ р-р₂

Положим, что р_} и р[ равны по модулю и действительны. Нуль пер­вого выражения находится в левой части плоскости р (рис. 10.6, о), а нуль второго р\=~~р_х — в правой части плоскости р (рис. 10.6, б). Пусть на вход обоих четырехполюсников воздействует синусоидальное напряже­ние частотой о>. Некоторой конкретной частоте на комплексной плоско­сти соответствует точка а на оси +J. Образуем разности р-р^ и р-р₂ на рис. 10.6, а и разности р- р\ и р- р₂ на рис. 10.6, б:

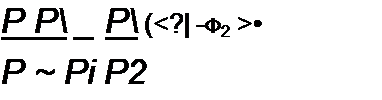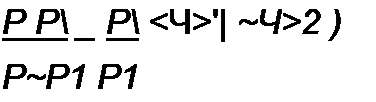Модули этих передаточных функций одинаковы и равны р”/ р₂ тог­да как аргументы различны. Аргумент ср, -<р₂ первого четырехполюс­ника меньше аргумента ф, ~<р₂ второго четырехполюсника. Четырехпо­люсник с передаточной функцией K^f(p) — м. ф., а четырехполюсник с К\р) — ^н- Ф- Пример н. ф. четырехполюсника — на рис. 10.7. Для него

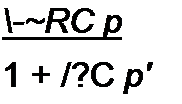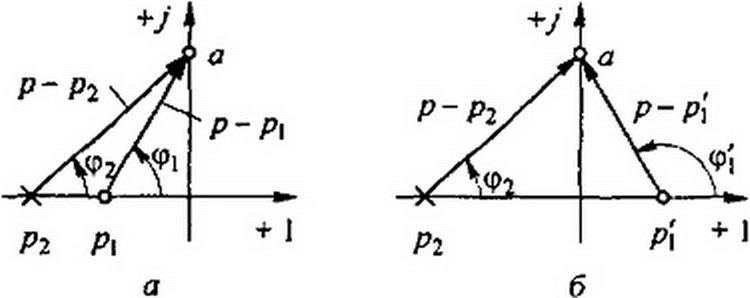В м, ф. четырехполюснике существует однозначная зависимость между модулем и аргументом передаточной функции. В н. ф. четырех­полюсниках между модулем и аргументом передаточной функции нет однозначной зависимости.

§ 10.7 Типы задач ло синтезу четырехполюсников. Синтез четы­рехполюсников включает в себя рассмотрение различных способов решения следующих групп задач:

§ 1.1 тез четырехполюсников по их передаточным функциям К(р);

§ 1.2 тез четырехполюсников, которые могут осуществлять либо толь­ко фазовую, либо только амплитудную коррекцию;

§ 1.3 тез четырехполюсников, обеспечивающих устойчивость рабо­ты системы.

Решение задач первой группы выполняется в два этапа. Первый этап состоит из аппроксимации частотной характеристики А'(р), которую хотят получить от четырехполюсника (два различных способа осуществ­ления этого этапа применительно к фильтрам рассмотрены в § 10.12). Второй этап состоит в реализации либо схемой с пассивными элемента­ми (например, схемой, рассматриваемой в § 10.8), либо схемой, содер­жащей и пассивные, и активные элементы (§ 10.9). Подход к решению задач второй группы рассмотрен в § 10.10 (фазовая коррекция) и в § 10.11 (амплитудная коррекция). Алгоритм решения задач третьей группы рас­смотрен, например, в [33].

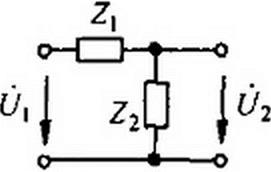
§ 10.8 Синтез четырехполюсников Г-образными ЯС-схемамн.

Г-образный четырехполюсник (рис. 10.8) является делителем напряжения. Его передаточная функция по напряжению при холостом ходе

Ш ₌ Z₂(p)

Ц(Р) Z|(p) + Z₂(p)'

В дальнейшем вместо Z;(p) и Z₂(p) будем писать соответственно Z] и Z₂.

Положим, что с помощью Г-образного четырех­полюсника, состоящего из RC-элементов, требуется реализовать передаточную функцию по напряжению при холостом ходе:

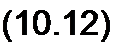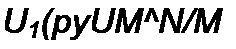где /V и Л/— полиномы по степеням р; У/Л/ удовлетворяет условиям, которые предъявляются к передаточной функции /?С-четырехполюсника.

Приравняем правые части (10.11) и (10.12):

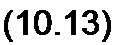У_ ₌ _^2_ М ~ Z\ + z₂ “

Разделим числитель и знаменатель правой части (10.13) на некоторый полином Q = Q(p), имеющий тот же порядок, что и полиномы У и Л/; корни его чередуются с корнями уравнений У = О и М = 0. Тогда

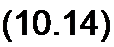Z₂ N/Q

Z,+Z₂ MIQ'

Из уравнения (10.14) находим Z₂ -N/Q и Z| = (М -N)/Q. Реали­зуем двухполюсники Zj и Z₂ по найденным операторным сопротивле­ниям^. Реализацию двухполюсников производят в соответствии с § 10.3 и 10.4.

§ 10.9 Синтез четырехполюсников по их К{р) схемами с ОУ в цепи обратной связи. Рассмотрим схему рис. 10.9, п, содержащую два линейных пассивных ЯС-четырехполюсника (/ и 2) и идеальный опера­ционный усилитель (ОУ). В цепь обратной связи включены ОУ и второй четырехполюсник. Положительные направления отсчета токов и на­пряжений на элементах схемы показаны стрелками. Один штрих в обо­значениях токов, напряжений и У-параметров четырехполюсников показывает, что рассматриваемая величина относится к первому четырех­полюснику, а два штриха — ко второму.

Запишем уравнения четырехполюсников в У-форме:

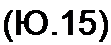для первого /; = X/j С/; + у;₂1/;, /₂ = У₂| Ц' + У₂₂^; для второго /;=Ун ЦЧУ₁₂ С/₂, Г₂ = У/, t7f + У₂₂ У₂.

Напряжение на входе схемы 1]^ равно напряжению на входе перво­го четырехполюсника, т. е. (j_вх = С/.', а напряжение на выходе первого четырехполюсника (Д равно напряжению на входе второго (7*, и оба эти напряжения равны нулю, так как являются напряжениями на входе ОУ. Кроме того, напряжение на выходе схемы (7_еых равно напряжению на выходе второго четырехполюсника t/₂, а ток Г₂ так как вход­ной ток ОУ равен нулю. Из (10.15) следует, что

/2=^1^вх И /Г=-/2=^21^_Ых.

Предполагаем, что полином Q(p) может быть найден и и Z₂ удовлетворяют усло­виям. перечисленным в § 10.2.

Учтем, что четырехполюсник 1 — взаимный, поэтому = ^12> ^{и П0}‘

лучим передаточную функцию схемы по напряжению

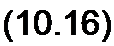Знак минус в (10.16) свидетельствует, что напряжения С/_вых и С/_ъх на­ходятся в противофазе (ОУ в инвертирующем включении). Поскольку параметры У₍₂ четырехполюсников могут быть выражены через параметр В и определитель Д = 1 уравнений четырехполюсников, записанных в Л-форме (см. § 4.7), т. е. У₁₂ = - Д, то К(р) можно записать и так:

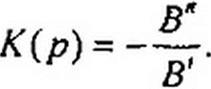В

(10.17)

В качестве примера составим К(р) для случая, когда первый четырехполюсник собран по схеме рис. 10.9, б, а второй — по схеме рис. 10.9, в. Учтем, что проводимость двух параллельно соединенных эле­ментов равна сумме их проводимостей, а при последовательном соеди­нении двух элементов проводимость равна произведению проводимос­тей этих элементов, разделенному на их сумму:

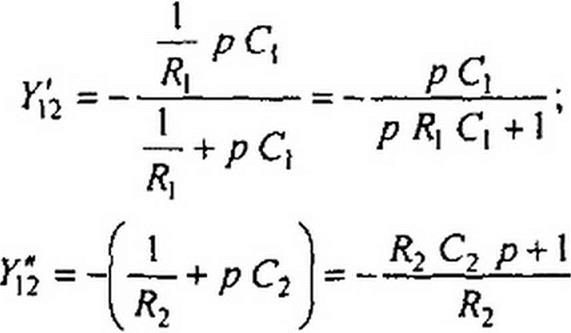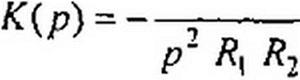
Подставим полученные выражения в (10.16):

______ ^2 Q Р _______________

С\ С₂ + р (/?| + Р-2 С₂) + I

§ 10.10 Четырехполюсник для фазовой коррекции. На рис. 10.9 изображена симметричная скрещенная схема из чисто реактивных двухполюсников Z, и Z₂, на выходе которой включен резистор сопро­тивлением R. Положительные направления токов и напряжений указаны на схеме.

В уравнении й'₂ + f_a = f_b Z₂ заменим </₂ на /₂ R и учтем, что /₂ = j_a - j_b. Это дает возможность выразить /_А через /_о :

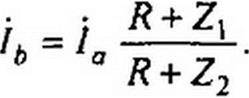Подставим /_А в /₂ = l_a-I_h и найдем

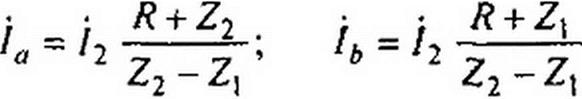Составим уравнение для периферийного контура:

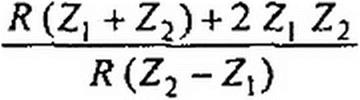Передача напряжения

Ц₂ R(Z₂-Z_}} (7, R(Z_X +Z₂) + 2Zj Z₂'

Входной ток

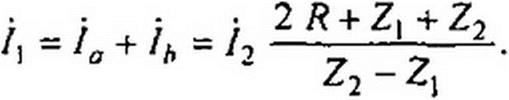Входное сопротивление

(7, ^/?(Z₁+Z₂)-b2Z₁Z₂
/] 2 R + Zj + Zj

Приравняв Z_BX = /?, получим соотношение Zj Z₂ = R². Из него сле­дует, что реактивные сопротивления Z_x и Z₂ взаимно обратны.

В формулу для К(, подставим Z₂ = R² IZ_X :

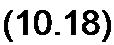= К„ (ш)

К + Z|

Так как Z₍ — чисто реактивное сопротивление, то модули числителя и знаменателя формулы (10.18) одинаковы и потому К_(/((о) = 1. При из­менении частоты о меняется только аргумент ф(<о)‘\ Четырехполюсник на рис. 10.10 служит для фазовой коррекции. С этой целью его включа­ют между источником питания с внутренним сопротивлением R и актив-

Обратим внимание на то, что знак ф(со) противоположен знаку аргумента b в выра­жении постоянной передачи g~a + jb четырехполюсника.

ной нагрузкой 7?, и он, не изменяя напряжение источника питания по мо­дулю, поворачивает его на требуемый угол <р(со) по фазе, осуществляя этим фазовую коррекцию.

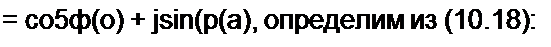Имея в виду, что - I; <

_{z = R} 1 - *7/ _{= R} 1 - cos ф(ы) - j sin ср<со) _{= R} ф(ы)
\ + К₍/ 1 + со$ф(с))+ j sin<p(o) 2

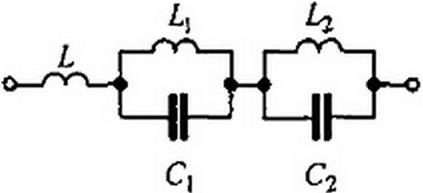
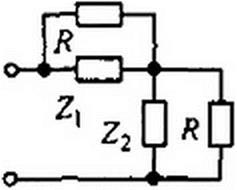
Сопротивление Z₂=R²!Z_{. Сопротивление Z_t = j X чисто реактивное. График X=f(<n) имеет вид тангенсоиды. При ф(со) = л, 2 я,... Д'изменяет знак. Иногда Z_: реа­лизуют схемой на рис. 10.11. Для определения параметров данной схемы составляют столько уравнений, сколько параметров неизвестно, и затем эти уравнения совместно ре­шают. Положим, что ф(е>) корректирующего четырехполюсника должна иметь значения Ф|(о>) при со,, ф₂((й) при си₂ и т. д. Тогда уравнения, которые нужно совместно решить относительно L, £_b L₂, C_it С₂. получают, если входное сопротивление схемы (см. рис. 10.11)

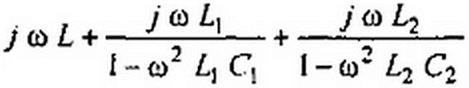последовательно приравнивать к Z_}--jR tg-^⁰^ при выбранных частотах. В результа­те система уравнений относительно I,, С|. С₂ имеет вид

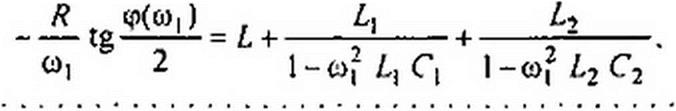§ 10.11 Четырехполюсник для амплитудной коррекции. Схема четырехполюсника, осуществляющая амплитудную коррекцию, изобра­жена на рис. 10.12. Корректор нагружен на резистор сопротивлением Я, входное сопротивление его также равно R. Сопротивления Z, и Z₂ ^вза* имно обратны (Z|Z₂=T?²). Постоянную передачу g=a+jb (см. § 4.10) в этом случае определяют по формуле

е^х =1 + Zi//?.

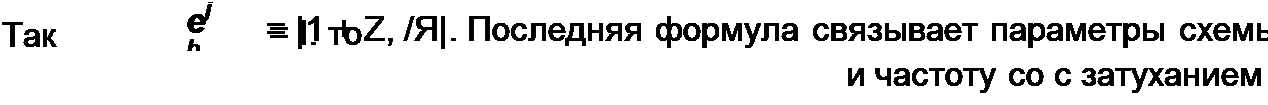сти оттого, что представляет собой сопротивление Z_}, характер зависи­мости а = /(©) оказывается различным. В качестве примера на

R R R R

а б в

Рис. 10.13

рис. 10.13, а-г изображены четыре схемы с различными Z_K и Z₂ и гра­фики соответствующих им зависимостей.

Схему амплитудного корректора выбирают в соответствии с той зависимостью а- /(со), которую необходимо реализовать. Параметры схемы корректора (например, сопротивление емкость конденсатора С_} для схемы на рис. J0.13, а) определяют путем совместного решения системы уравнений, полученных приравниванием модуля величины значению е° при фиксированной частоте со. Уравнений со­ставляют столько, сколько в Z_t неизвестных параметров. Уравнения имеют вид:

11 + Z, IRI =e^a(w,), Il + Z, /R = е^0(<|>:), ....

I ¹ Ю>| • ¹ 0)₂

Частоты coj,co₂,... выбирают для характерных точек зависимости a- /(<$) либо через равные интервалы.

§ 10.12 Аппроксимация частотных характеристик. Аппроксимация — это прибли­женная замена заданной частотной зависимости другой частотной зависимостью, которая точно совпадает с заданной в ограниченном числе точек, отклоняется от нее в допусти­мых пределах вне этих точек, давая в то же время физически реализуемую функцию. На­пример, кривая (Л7(/со) [ на рис. 10.14, а — это частотная характеристика идеального фильтра НЧ | K{J х) | = Дх). где K(j х) —передаточная функция; х = (о/о_с, где о_с — безразмерная величина, равная частоте среза.

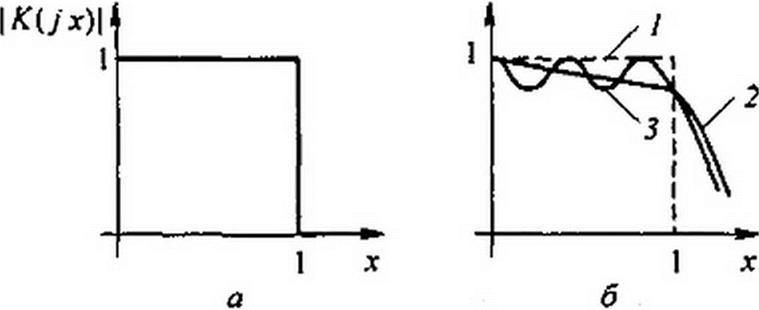
Рис. 10.14

В диапазоне изменения х от 0 до 1 |j<(j x)l = I; при _х> I |К(У х)| = 0. Штриховая линия (рис. 10.14, 6) повторяет кривую на рис. 10.14, а, кривая 2 характеризует гладкую аппроксимацию, при которой отклонение от кривой 1 неодинаково в диапазоне аппрокси­мации. Кривая 3 иллюстрирует равноволновую аппроксимацию, при которой абсолютные значения максимальных отклонений от средней линии в обе стороны одинаковы. Гладкую аппроксимацию осуществляют обычно полиномами Баттерворта, равноволновую — поли­номами Чебышева. Известны и другие способы аппроксимации [10], у каждого из них име­ются свои достоинства и недостатки.

Гладкая аппроксимация. Применительно к фильтру НЧ аппроксимацию квадрата модуля передаточной функции четырехполюсника осуществляют так:

ко х)|²

Принимают, ^то при x=l [£(j х)| = 1/г/2, откуда /и = 1. Полагая p = jx, найдем полюсы |А’(/х)| :

K(j х) К(-/ х) =

При нечетных п

p_k =1^)/2" ^_c^jkKl,> к =0,1.................... п;

при четных п

Р_к = (-1)^,/(2"> = е ²" , * = 0.1,...,и.

Полюсы расположены симметрично по окружности единичного радиуса. Полиномы (р-р\)...{р-р„) образуют знаменатель K{j х) и называются полиномами Баттервор­та. При составлении их используют значения р, находящиеся в левой полуплоскости. Это обеспечивает физическую осуществимость К(р\ Запишем полиномы: при п = 1 —р + 1; при п = 2 — р² +J1 р + 1; при п-3— р³+2р²+2р + 1.

Задаваясь требуемым затуханием фильтра в децибелах (обычно при х = 2) а = 10 lg(l/| Ш₂)². определим п:

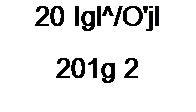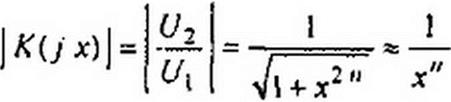Например, при а = 18 дБ и = 18/(20 Ig2) = 2.98 * 3. В рассматриваемом примере

ад=-5--------------- ; •

р³ + 2 р“ + 2 р+ 1

Функцию К(р] реализуют известными методами.

Равноволновая аппроксимация. Полиномы Чебышева порядка п записывают в триго­нометрической форме:

Т„(х) - cos п arccos х.

Полагая arccosx = 9 и имея в виду, что cosп0 = cos" 0- ^П cos"’² 0 sin² 0 +..., а sin0 = д/1 - х², получим алгебраическую форму записи полиномов:

Г„(х) = х" + С² х"“² (х² - 1) + С* х"’⁴ (х² -1)² + ....

Например, при п = 5 Т₅ (х) = 16 х² - 20 х³ + 5 х.

Так. Г„(х) колеблется от 1 до -I в интервале х = 0*| (рис. 10.15. а) и монотонно возрастает при х > 1.

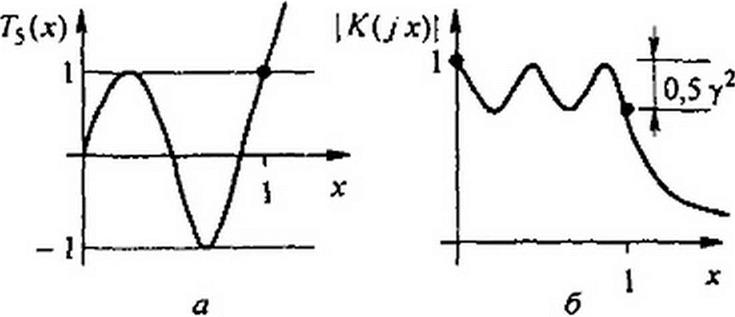Квадрат модуля нормированной передаточной функции фильтра НЧ с помощью поли­номов Чебышева аппроксимируют так:

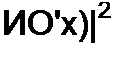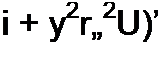Максимальное отклонение |/v(jx)| от 1 равно у-/2

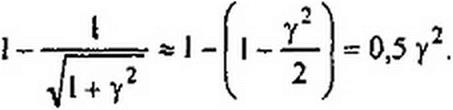При х > 1, т. е. в области затухания фильтра НЧ,

у² Т„{х) » 1 и I K(j х) I = —-— = —-—!-------------------------- .

У Цх) у ch(n Arch х)

Примерный вид аппроксимирующей кривой \K{j х)| показан на рис. 10.15, б.

Для заданного отклонения у и затухания а в децибелах при .г = 2 а = 20 lg| U_t/U₂ i ~ 20 lg[ l/K(y 2)j порядок полинома Чебышева определяют по фор­муле

। _1о«/2О

п -------- Arch----------- ,

где 1,32- Arch 2.

Например, для у = 0,4 и а = 30дБ при х-2 | K(j x)J = 0.03!8;

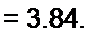¹ a J0 п =--- Arch-----------

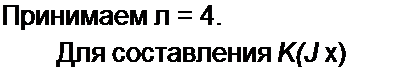1.32 0,4

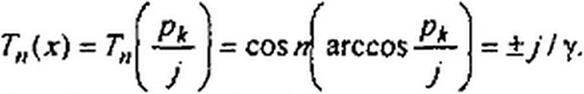
следует определить полюсы [ K(J х) |², находящиеся в левой х = р_к / j и приравняем к нулю знаменатель

При х>1 Г„(х) = Г„(р_А/y) = chnArch(p_A/y).

Так как р_к — комплексное число, то arccosp* /у — тоже комплексное число, кото­рое положим равным а_Л + J$_k. Тогда

Т_п(р_к //) = со5(ла* +■ jл Р>)-cosset* сБл0> - /sin и a* sh п pj = ±у'/у. Отсюда

cos n a* ch n Р* = О, sin л а* sh п Р* = ±1/у.

Так как chap* *0, то

cos«a_A=0 и а* = (2 к + 1) А =0,1,..., и. 2 п

При этом

sin/ra* =±1; sh«pj=l/y; Р> = ~ Arsh(l/y). л

Так как

arccos(p*/j) = а* +/₽*.

ТО

Рк = а_к + j b_k = j cos(a_A + j Р_А).

Действительные и мнимые части полюсов р_к, лежащих в левой полуплоскости:

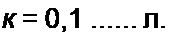а_к = -shp* sin(2к +1) —; P_t=ch0tco$------------------------------------------------------------------ —

2 и 2 л

Из последней строчки следует, что а_к /sh² р* +b_k /ch² p_t = I. т. е. полюсы р_к распо­ложены на эллипсе, одна полуось которого равна sh Р*. другая — ch р_Л.

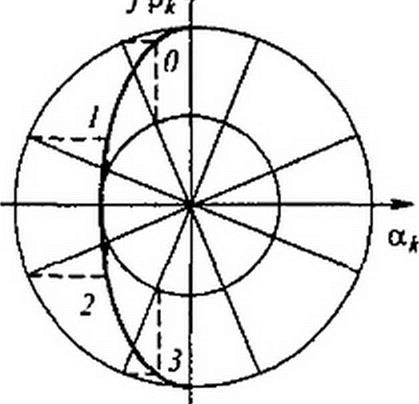
В рассматриваемом примере при п-4 и у = 0,4 0* =0,412; shp* =0,421; ch р* = 1,08.

Для построения эллипса чертим две окружности, одну радиусом sh0*, другую радиусом ch 0* (рис. 10.16), и через начало координат проводим прямые до пересечения с окружностями под углами

= (2 к + 1) (л/2 л), где к = 0, 1..... л. В примере а_Л *22,3;67; 111; 156°.

Из точек пересечения лучей с окружностью мень­шего радиуса проводим вертикали, а из точек пересе­чения с окружностью большего радиуса — горизонта­ли. Точки пересечения соответствующих юризонталей и вертикалей на левой полуплоскости дают искомые полюсы. В примере p_{Q 3} - -0.164± у 0,995; р) 2 =-0,388± у 0,416. Нормированная передаточная функция

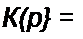_________________ 1________________

(Р~Ро){Р~Рз)(р-Р_>)(Р-Р2>

____________________ 1___________________

((р + 0,164)² + 0,995²) ((р + 0,3 88)² + 0,416²)'

По К(р) определяют схему и ее нормированные параметры £_н, С_н. Таблицы поли­номов знаменателя нормированного К(р) низкочастотных фильтров, аппроксимирован­ных различными способами, даны, например, в [10]. Для перехода от нормированных к действительным параметрам L, С пользуются соотношениями L = £_н/о_с и С=С_и/о_с.

Какому способу синтеза схемы и какой конкретной схеме следует отдать предпочте­ние, зависит не только от стоимости и габаритов при практическом осуществлении схе­мы. но и оттого, насколько фазочастотные характеристики получающихся четырехполюс­ников удовлетворяют поставленной задаче.

В заключение отметим, что нормирование распространяется не только на передаточ­ную функцию четырехполюсника, но и на другие функции, в частности на входное сопро­тивление или проводимость двухполюсников.

Если аппроксимируют не передаточную функцию, а входное сопротивление (прово­димость) некоторого двухполюсника, то оно обычно нормируется не только по частоте ы₀-

но и по его числовому значению. При нормировании Z(p) по числовому значению вход­ное сопротивление (проводимость) делят на некоторую безразмерную величину Л_н. При переходе от схемы, реализующей нормированное сопротивление Z_K (ее параметры Я_к, Л_и, С_н и частота х), к той же схеме, но с ненормированными параметрами (ее сопротивление

Z, а параметры R, L, С), последние определяют, сопоставив почленно одинаковые слага-

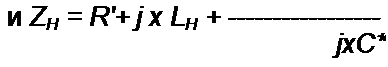
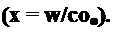Z R j <а L 1 емые “ =—— ⁺---

Ro Ro Ro j © C R$

В результате получим R = R_H R_o; L- L_H (Я_о /w₀); C = C_H /{R^ ca₀), где <o_o — вели­чина безразмерная.

Вопросы для самопроверки

1. Укажите два основных направления развития синтеза электрических цепей. 2. Оп­ределите задачи синтеза, перечислите условия, которым должны удовлетворять Z(p) фи­зически реализуемых двухполюсников. 3, Поясните идею реализации двухполюсников лестничной схемой. Покажите, как следует упорядоченно определять ее элементы. Любое ли Z(p) может быть реализовано лестничной схемой? 4. Как осуществить реализацию путем последовательного выделения простейших составляющих? 5. Нарисуйте две кано­нические схемы двухполюсников, отображающие идеи реализации методом выделения простейших составляющих. 6. В чем идея реализации методом Бруне? 7. Какой четырех­полюсник называют минимально-фазовым? 8. Сформулируйте, какие типы задач возникают при синтезе четырехполюсников. 9. Поясните этапы вывода формулы (10.17) для схемы рис. 10.9, а. 10. Определите К{р) четырехполюсника рис. 10.9, а, если в четырехпо­люснике Z, (рис. 10.9, б) последовательно соединены Л,, С| и I,, а второй четырех­полюсник оставлен без изменений. 11. Начертите схему четырехполюсника для фазовой коррекции и поясните, как определить ее элементы, если известна зависимость ф(<о). 12. Изобразите схему амплитудного корректора и расскажите, как определить ее элемен­ты, если известна зависимость а(©)- 13. В чем состоит задача аппроксимации и как она решается? 14. Поясните идею составления К(р} четырехполюсника, если в основу положена: а) гладкая аппроксимация; б) равноволновая аппроксимация. 15. Как от норми­рованных параметров перейти к ненормированным, задавшись некоторыми и га₀? 16. Решите задачи 12.3; 12.6; 12.10; 12.7; 12.14; 12.17; 12.28.

Глава одиннадцатая

УСТАНОВИВШИЕСЯ ПРОЦЕССЫ

В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ