Синтез электрических цепей
§ 10.1. Характеристика синтеза. Синтезом линейной электрической цепи называют определение структуры цепи и числовых значений составляющих ее элементов R, L, С по известным операторным или временным характеристикам этой цепи при воздействии на вход напряжения определенной формы. Одному и тому же операторному выражению, принятому в качестве исходного при синтезе, могут соответствовать несколько различных схем разной структуры. Поэтому, после того как получено несколько решений, выбирают из них наиболее подходящее. Чаще всего критериями при окончательном выборе схемы являются стоимость, габариты и масса устройства, а также чувствительность при изменении того или иного параметра схемы.
Задачи синтеза ставят и решают в теории сложных фильтров, в теории корректирующих контуров в автоматике, связи, радиотехнике, а также в кибернетике при создании предсказывающих и сглаживающих устройств.
Синтез развивался главным образом по двум направлениям:
1) известным операторным функциям (по Z(p) для двухполюсников и передаточной функции для четырехполюсников);
2) временным характеристикам, т. е. по известному временному отклику системы при воздействии единичного напряжения.
Эти два направления взаимно дополняют и развивают друг друга. В настоящее время наибольшие результаты достигнуты на первом из упомянутых направлений.
В § 10.2-10.9 даны основные сведения о синтезе цепей по заданной операторной функции (более полно об этом см., например, [6]). Методика синтеза цепей по заданным временным функциям здесь не рассматривается (для ознакомления с ней следует обратиться к специальным руководствам).
В теории автоматического регулирования распространен синтез, основанный на использовании логарифмических частотных характеристик, в импульсной технике подбор параметров электронных и полупроводниковых схем, т. е. в известном смысле синтез этих схем, производят, используя спектральный метод, рассмотренный в гл. 9,
3) 10.2. Условия, которым должны удовлетворять входные сопротивления двухполюсников. Если представить входное сопротивление двухполюсника в виде отношения двух полиномов, расположенных по убывающим степеням оператора р,
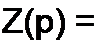
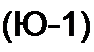 А'(Р) _ Р" р"~' +... + Q1
А'(Р) _ Р" р"~' +... + Q1
М(р) Ьт р'" + pm~'+... + by р + Ь^' то должны выполняться следующие пять условии:
1) все коэффициенты а и b в числителе и знаменателе должны быть неотрицательны (в дальнейшем будет ясно, что условие 1 следует из условия 3);
2) наивысшая (наименьшая) степень полинома числителя (и) не может отличаться от наивысшей (наименьшей) степени полинома знаменателя (т) более чем на единицу;
3) если условиться значения р, при которых Z(p) = 0, называть нулями функции Z(p), а значения р, при которых Z(p) = со, — полюсами Z(p), то нули и полюсы должны быть расположены только в левой части плоскости р\
4) нули и полюсы, расположенные на мнимой оси плоскости р, должны быть только простые, не кратные;
5) если вместо р в выражение Z(p) подставить j <в, то при любом значении со должно быть ReZ(j(o)>O.
Поясним эти требования. Из § 8.11 известно, что свободные процессы описываются слагаемыми вида Ак ер‘' и обязательно должны затухать во времени; рк— корни уравнения Z(p)-0. Но затухать свободные процессы (слагаемые вида Ак еРк') могут только в том случае, когда действительная часть рк отрицательна. Отсюда следует, что нули уравнения Z(p) = 0 должны обязательно находиться в левой части плоскости р.
Поскольку каждому планарному двухполюснику соответствует дуальный, а входная проводимость дуального двухполюсника У(р) = Z(p)/A, где к — некоторый коэффициент, имеющий размерность Ом в квадрате (см. § 3.43), то входное сопротивление дуального двухполюсника равно к/2{р). Нули дуального двухполюсника, являющиеся полюсами исходного, также должны быть расположены в левой части плоскости р.
Из курса математики известно, что если имеются два кратных корня уравнения N(p) = 0, то соответствующие им слагаемые в решении берут в виде (С[ + С2 1) ер‘. Если допустить, что на мнимой оси могут быть два кратных корня р = j 0, то соответствующая им свободная составляющая (С] +С2 /)еур' нарастала бы до бесконечности, чего физически быть не может. Коэффициенты а и b в числителе и знаменателе Z(p) должны быть положительны. Если бы это условие нарушилось, то на основании леммы, вытекающей из теоремы Гурвица (см. § 17.2), среди корней уравнения Z(p) - 0 появились бы корни с положительной действительной частью.
Поясним, почему степень т не может отличаться от степени более чем на единицу. Допустим, что степень т больше степени п на два. Тогда р —> оо является нулем второй кратности для Z(p), а то, что происходит при р °0, можно считать происходящим на мнимой оси плоскости р (мнимая ось простирается в бесконечность). Но тогда на мнимой оси получается кратный корень, чего быть не может.
Проведя такое же рассуждение для дуального двухполюсника, убедимся, что степень п не может быть больше степени т более чем на единицу.
Если в Z(p) вместо р подставить j со, то Z(j со) будет представлять собой комплексное сопротивление двухполюсника в установившемся синусоидальном режиме при частоте со, a ReZ(jco)—действительную часть входного сопротивления. В том случае, когда двухполюсник содержит резистивные сопротивления, его ReZ(j со) > 0 (он потребляет активную мощность /2 ReZ(j со) ). Если же двухполюсник чисто реактивный, то Re Z(J со) = 0. В общем случае для пассивного двухполюсника всегда должно быть ReZ(y со) > 0.
В литературе по синтезу цепей иногда пользуются термином «.положительная действительная (вещественная) функция». Под ней понимают функцию:
^действительная часть которой положительна, если положительна действительная часть р;
2) действительная при действительном (не комплексном)р. Поскольку 7(р)этим свойствам удовлетворяет, оно является положительной действительной функцией.
Пример 111. Задано несколько выражений вида R(p)/M(p). Выяснить, могут ли они представлять собой входные сопротивления некоторых двухполюсников:
1) 5Р~6 • 2) 204-12 р + 6
25р2 +12р + 2' 12 р4+8 р3 + 12 р2+13 р +1'
3) . 4) 2р2 + р+\
р3 + р2 + р+Г (p+i)(p2+i)
Решение. Первое выражение не может представлять собой Z(p), так как один из коэффициентов в числителе отрицателен. Второе и третье выражения также не могут представлять собой Z(p): второе потому, что максимальная степень р в знаменателе больше максимальной степени р числителя на два, третье потому, что
|
|
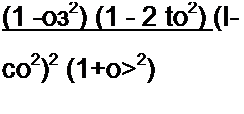 |
при значениях w от 0,707 до 1 отрицательно. Четвертое выражение всем требованиям удовлетворяет и потому может представлять собой Z(p) некоторого двухполюсника.
Кроме названных общих свойств перечислим свойства Z(p) двухполюсников, состоящих только из R и С, только из R и L и только из L и С. Двухполюсники типа RC и R L имеют чередующиеся простые нули и полюсы на отрицательной вещественной оси плоскости р. Для R С -двухполюсников ближайшей особой точкой к началу координат является полюс, в бесконечности полюс отсутствует. Для двухполюсников типа R L ближайшей к началу координат особой точкой является нуль, при р = 0 полюс отсутствует. Двухполюсники типа L С имеют чередующиеся простые нули и полюсы на мнимой оси. Степени полиномов числителя и знаменателя отличаются на единицу.
Нули и полюсы Z(p) можно изобразить условными значками на комплексной плоскости, скажем, нули кружками, полюсы крестиками. Полученную картину называют картой нулей и полюсов. Эта карта наглядно характеризует частотные свойства двухполюсника и реакцию его при воздействии единичного напряжения.
По расположению и количеству нулей на ней можно определить число апериодических и колебательных компонент, которое содержит свободная составляющая, и быстроту затухания той или иной из них во времени. Чем ближе к мнимой оси расположены нули, тем медленнее затухает соответствующая им свободная составляющая.
Существует несколько способов реализации двухполюсников по заданной Z(p), удовлетворяющей перечисленным в § 10.2 условиям. Три основных способа реализации рассмотрены в § 10.3-10.5.
§ 10.3. Реализация двухполюсников лестничной (цепной) схемой. Познакомимся с понятием непрерывной дроби. Непрерывной называют дробь вида
1
1
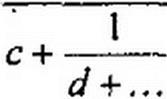 |
Входное сопротивление или входная проводимость лестничной (цепной) схемы по типу рис. 10.1, а, в которой продольные сопротивления названы Z(, Z3, Z5,..., а поперечные проводимости— У2, У4, У6,...,— могут быть представлены непрерывной дробью.
Для того чтобы убедиться в этом, проделаем небольшие выкладки. Найдем входную проводимость правой части схемы по отношению к зажимам тп. Она равна
z5 + i/r6‘
Суммарная проводимость правой части схемы по отношению к зажимам тп с учетом ветви с проводимостью У4 равна
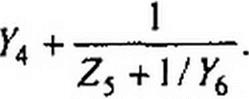 |
Входное сопротивление по отношению к тем же зажимам
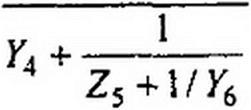 |
|
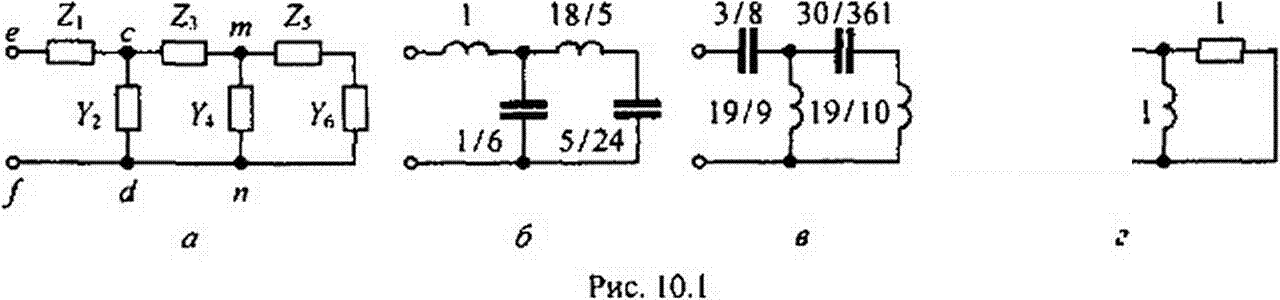 |
 | |||||
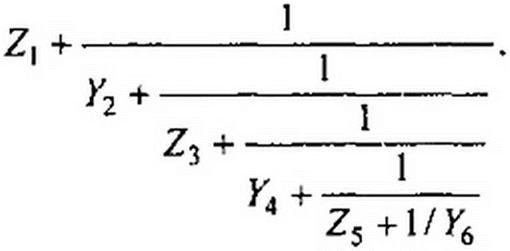 | |||||
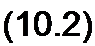 | |||||
Таким образом, возникает задача о переходе от (10.1) к (10.2), т. е. задача о последовательном упорядоченном определении элементов лестничной схемы ((Zb Zb Z5,У2, YA, К6,...) по выражению (10.1), С этой целью:
1) располагаем полиномы /V(p) и М(р) по убывающим либо по возрастающим степеням р;
2) делим многочлен на многочлен, следя за тем, чтобы в процессе деления получались положительные (не отрицательные) слагаемые и чтобы они не содержали р в степени больше 1 и меньше -1;
3) учитываем, что если в процессе деления возникнет необходимость перейти от расположения полиномов по убывающим степеням к расположению их по возрастающим степеням, то эта операция вполне допустима.
При делении полинома на полином М будут получены частное Z, и остаток О\! М, т. е.
7 N 7 О} _ _ 1
Z — — = Z, + — — Z> н— .
м м м/о}
При делении М /О, будет получено частное У2 и остаток
О} ОХЮ2‘
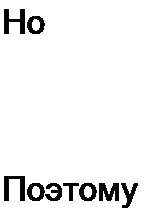 | |||
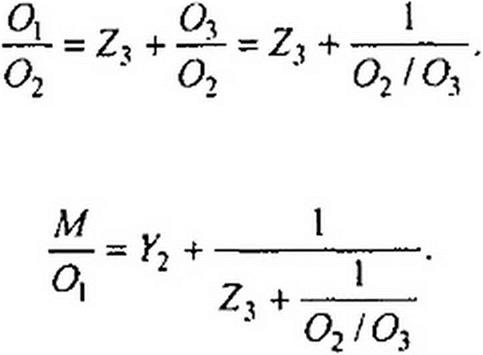 | |||
На основании изложенного процесс последовательного определения элементов можно представить следующей схемой:
M
Л /Z, |z,
A/|(9i
Oy y4
Пример 112. Определить параметры лестничных схем, для которых р4 +9 р2 +8
Z(p)~-—’ располагая сначала при делении полиномы по убывающим, а затем Р +3р
(для реализации второй схемы) по возрастающим степеням р. Как будет видно из дальнейшего. в процессе деления в обоих случаях не возникнет необходимости в переходе от расположения по убывающим к расположению по возрастающим степеням р.
Решение. Выполним деление, расположив слагаемые по убывающим степеням р:
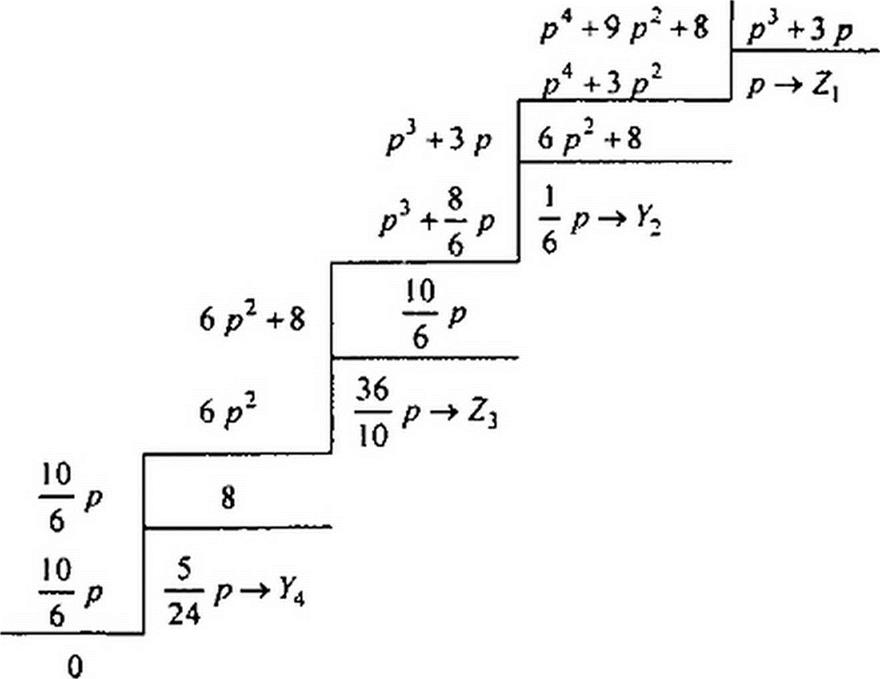
На рис. 10.1, б изображена схема, где указаны значения индуктивностей (Гн) и емкостей (Ф). полученные при делении, когда слагаемые были расположены по убывающим степеням. Так как примеры имеют чисто иллюстративный характер, то не следует обращать внимание на то, что индуктивности и емкости в примерах достигают практически трудно осуществимых значений. Кроме того, реализуемые здесь 2(р) можно рассматривать как нормированные по частоте и значению (см. § 10.9). В этом случае от нормированных Ли. Сн параметров переходят к действительным, осуществить которые практически уже не составит труда.
Схема и параметры для второго случая, когда при делении слагаемые расположены по возрастающим степеням р, даны на рис. 10.1, в.
Рассмотрим пример, который является иллюстрацией того, что иногда в процессе деления возникает необходимость изменения порядка расположения слагаемых.
Пример 113. Требуется реализовать лестничной схемой
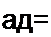 2р3+Зр2+2р + 1
2р3+Зр2+2р + 1
2 р2 + 2 р + 1
Решение.
2 р3 + Зр2+2р + 1 2 р2 + 2 р +1
2 р3 +2 р2 + р p-+Z,
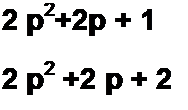 р2 + р +1
р2 + р +1
2
Так как получаем отрицательные слагаемые, дальнейшее деление прекращаем и переходим к расположению по возрастающим степеням
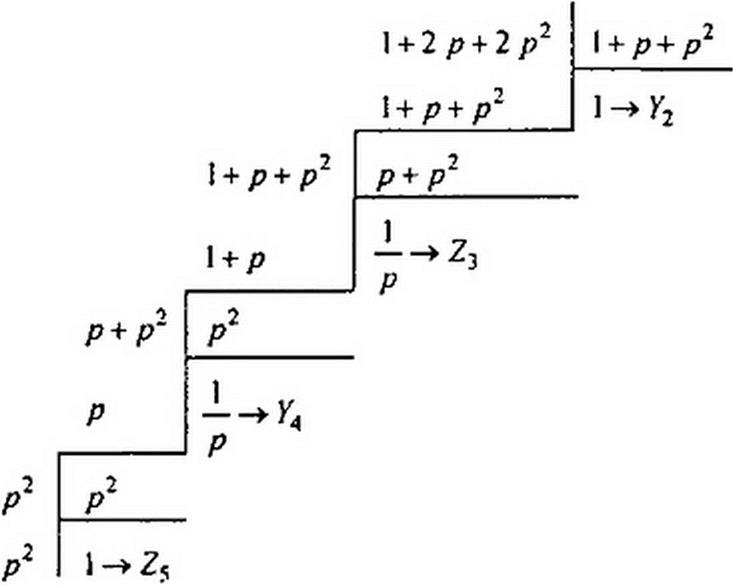 |
|
В заключение отметим, что могут встретиться такие Z(p), которые невозможно представить лестничной схемой, В этом случае применяют второй способ реализации, описанный в § 10.4. (Второй способ применяют не только в случае невозможности представления Z(p) лестничной схемой.) Если и он окажется неприменимым (например, при комплексных нулях и полюсах), то следует воспользоваться методом Бруне (см. § 10.5) или другими методами.
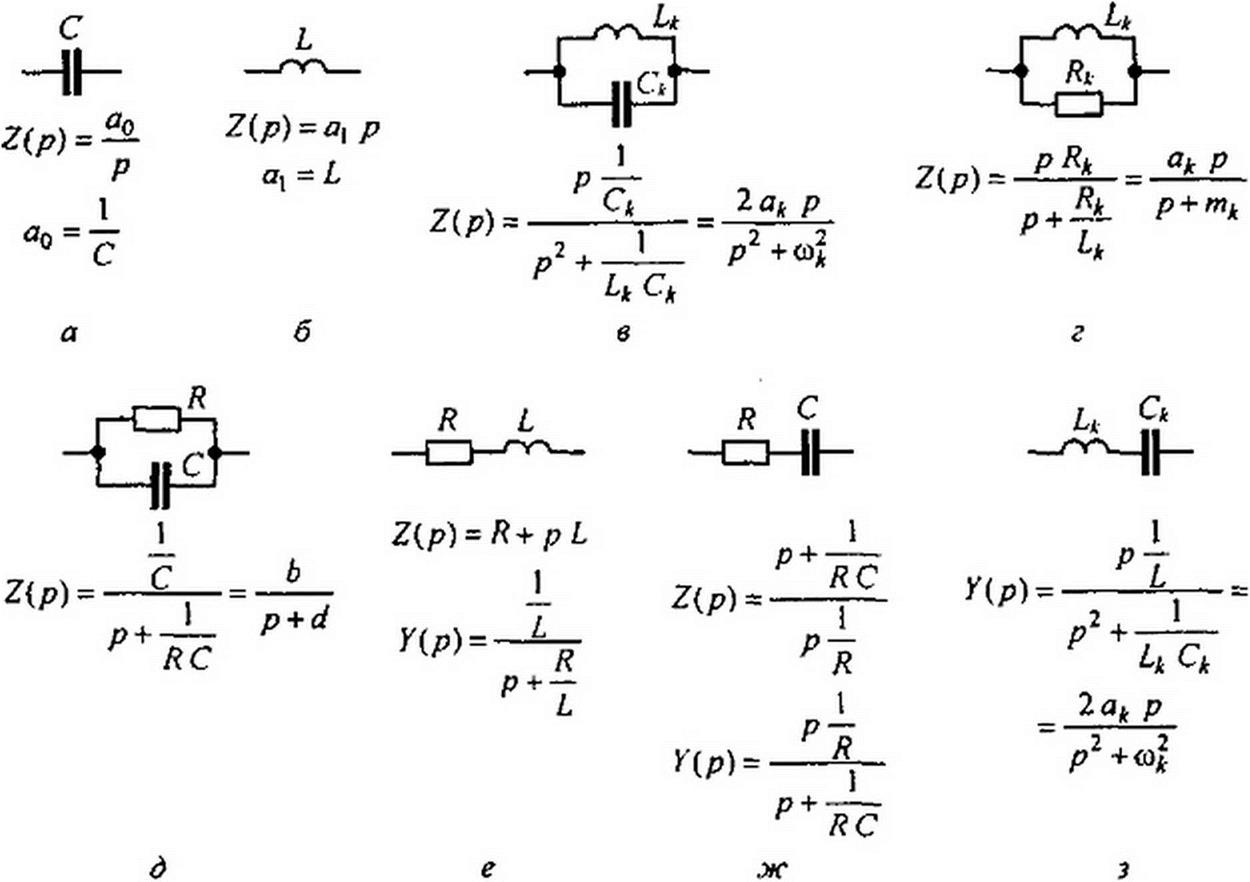
§ 10.4. Реализация двухполюсников путем последовательного выделения простейших составляющих. В качестве введения ко второму способу реализации двухполюсника запишем операторные сопротивления для простейших одно- и двухэлементных двухполюсников. На рис. 10.2, а~д изображены простейшие двухполюсники и записаны соот-
 |
|
ветствующие им операторные сопротивления; на рис. Ш.2, е, ж — сопротивления и проводимости и на рис. 10.2,5 — проводимость. Для рис. 10.2, а С = 1/о0, для рис. 10.2, б L = ah для рис. 10.2, в 2 ак = \!Ск и (з)2к = \/(Lk Ск\ для рис. 10.2, г ак = Rk и mk~Rk!Lk, для рис. 10.2, д Ь = \!С и d = \!RC.
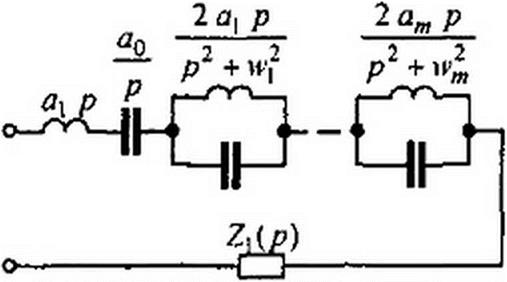
Сущность метода состоит в том, что заданное Z(^>) представляют в виде (рис. 10.3, о)
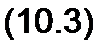 Z(p) = а, р + ^- + Х~22" + 21(Р>
Z(p) = а, р + ^- + Х~22" + 21(Р>
Р р + (1) д.
Первому слагаемому П; р соответствует последовательно соединенный индуктивный элемент индуктивностью а,, второму — последовательно соединенный емкостный элемент емкостью 1 / а0. Каждому 2 а к р
слагаемому вида —у-------- у соответствует последовательно соединенным
Р + ®к w 2 ак р
параллельный резонансный контур (слагаемому —г------------------------------------------------------------ у — пара полю-
Р
сов А,2 = находящихся на мнимой оси плоскости р). Сопротивление Z|(p) уже не содержит полюсов на мнимой оси. Функцию Z](p), среди полюсов которой нет полюсов, находящихся на мнимой оси, называют функцией минимального реактивного сопротивления. Возможны следующие варианты для Z|(p) \
’* 8 пунктах а-в полагаем, что коэффициенты ak. Ьк и Ьо действительны и положительны.
а) Z, (p) - У осуществляют последовательным соединением двухполюсников (рис. 10.2, г);
б) 7|(^) = Х—~— реализуют в виде резистора сопротивлением bQ P + dk
и последовательно с ним соединенных двухполюсников (рис. 10.2, д);
в) Z^p) = bQ осуществляют в виде резистора сопротивлением 60. 7( п\ Индуктивность = lim ■■ • (рис. 10.3, а).
р-т р
 |
|
 |
Величину а0 в схеме на рис. 10.3, а определяют как интегральный вычет функции Z(p) =/У(р)/Л/(р) в полюсе /7 = 0:
а0 = ResZ(p) = Л/(0)/Л/'(0), или = lim р Z(p).
/>-0
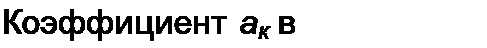 |  |
ту функции Z(p) в полюсе р = J ($к (ему же равен вычет функции Z(/?)
при p~-j так как они оба действительны):
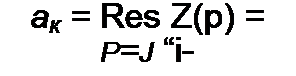 | |||
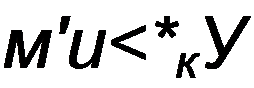 | |||
После того как найдено ак, можно определить Lk и Ск двухполюсника (см. рис. 10.2, в): Ск = 1/(2 ак\, Lk - \I(цу2 Ск).
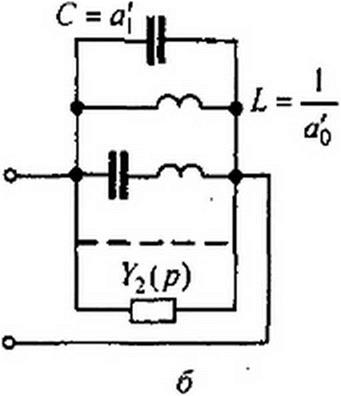
Реализацию двухполюсника можно осуществлять не только по его входному сопротивлению Z(p), но и по его входной проводимости У(/?) = 1/Z(p). Входную проводимость У(р) представляют в виде схемы на рис. 10.3, б:
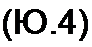 Пр) = 4 P + — + Y \а>< +У2(Р)-
Пр) = 4 P + — + Y \а>< +У2(Р)-
Р Р
В соответствии с правой частью (10.4) двухполюсник осуществляют в виде параллельного соединения емкостного элемента a'lt индуктивного двухполюсников на рис. 10.2, з (им соответствуют слагаемые 2а'к р вида —г--- у ) и двухполюсника минимальном реактивной проводимос-
ти К2(р), Н? содержащего полюсов на мнимой оси. Коэффициенты а'§ и ак находят путем вычисления интегральных вычетов функции Х(р) соответственно при р -0 и р - j соЛ, а С = а, - Нт У(р)/р.
р—^сО
Если функция У2(р) = У------------- , то ее реализуют в виде параллельно-
р + п
го соединения двухполюсников (см. рис. 10.2, е). Если функция
Х2(/2) - Xто ее реализуют параллельным соединением двухпо- р + s
люсников (см. рис. 10.2, ж)'\ Следует иметь в виду, что при реализации двухполюсника по его Z(p>) в виде последовательного соединения простейших двухполюсников начиная с некоторого этапа, может оказаться целесообразным перейти от сопротивления к проводимости и дальнейшую реализацию осуществлять уже параллельно соединенными двухполюсниками. Потребность в таком переходе может возникнуть, например, когда остающаяся для реализации часть Z(p) имеет нуль при p~Q. Этому нулю соответствует полюс У(р)при р = 0, который реализуют индуктивным элементом.
Пример 114. Реализовать Z(p) = —------------- .
р (р- + 2 р + р)
Решение. Так как Z(p) имеет полюс при р - 0. то в схеме может быть выделен последовательно включенный конденсатор емкостью С=1/о0. где aQ = ResZ(p) = 2/2 = I.
/>=0
Функция Z(p) не имеет полюсов, лежащих на мнимой оси. Поэтому в состав его не входят последовательно включенные двухполюсники (см. рис. 10.2, в). Определим, какое Z(p) осталось реализовать, обозначим его
Р р“ + 2 р+ 2
Функция Z3(p) имеет нуль при р = 0. Для реализации оставшейся части схемы
перейдем к проводимости Х3(р) =------------------------------------------------------------------------- Полюсу этой проводимости при р = 0
р(р + 2)
соответствует индуктивный элемент индуктивностью а'о =Ке$У3(р) = 1.
Осталось реализовать
Мр) = Г3(р) - - А.
р р{р + 2) р + 2 р + 2
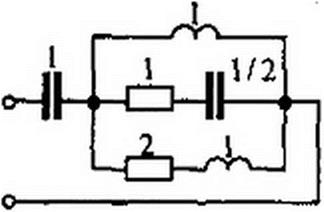
Слагаемому р/{р + 2) в соответствии с рис. 10.2, .ж- отвечает ветвь из последовательно соединенных R = I Ом и С = 5Ф. В соответствии с рис. 10.2, е проводимости 1/(р + 2) отвечает ветвь с Z. = 1 Гн и R = 2 Ом. Полученная схема изображена на рис. 10.4, а.
pi + л2 + 2 р
Пример 115. Реализовать Z(p)~ —— ---------------------------------------------------------------------------------- .
pi + р2 + р +1
’* Полагаем, что коэффициенты т и г действительны и положительны.
 |
|
 |
|
 |
|
Решение. При р ~ 0 у Z(p} нет полюса, поэтому последовательно включенный конденсатор у искомого двухполюсника отсутствует. Функция Z(p) имеет два полюса Р},2 ~ ±J' расположенных на мнимой осн. Выделим параллельный резонансный контур (см. рис. 10.2, в), соответствующий этим полюсам:
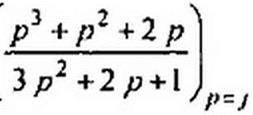 |
|
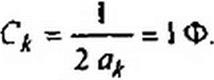 |
|
о* — 1: Z.* = I /(со* С*) = I Гн.
Найдем функцию минимального реактивного сопротивления:
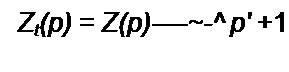 | |||
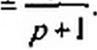 | |||
|
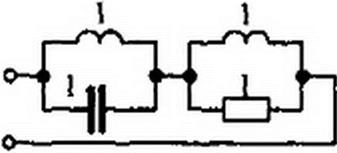
В соответствии с рис. 10.2, г реализуем Z}(p) в виде параллельного соединения R = (Ом и L = 1 Гн. Схема искомого двухполюсника изображена на рис. 10.4, б.
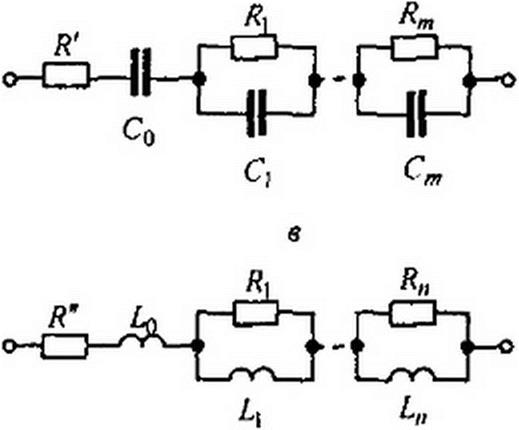
Двухполюсники, состоящие только из R и С, могут быть реализованы, например, канонической схемой на рис. 10.4, в, а состоящие из Я и L — схемой на рис. 10.4, г. Для схемы на рис. 10.4. в
; Л = —!—; R' - litn Z(p);
‘ С*’ ‘ RtCk'
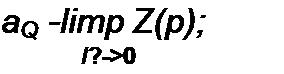 | |||
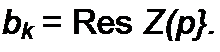 | |||
Для схемы на рис. 10.4, г
Z(p)=R’ + pL,1 +
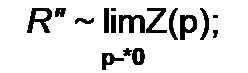 | 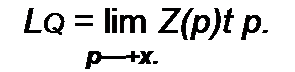 | ||
Параметры Rk и Lk находим, имея в виду, что сопротивление------------------------------------
Р + тк соответствует параллельному соединению Rk и Lk> где ак = Rk; mk=Rk/Lk\ ак - Res Z(p)l р.
§ 10.5 Метод Бруке. Основные этапы метода Бруне следующие.
1. Прежде всего проверяют, не содержит ли заданное Z(p) (назовем eroZJW(p)) полюсов на мнимой оси. Если они имеются, то из состава Z^(p) выделяют соответствующие этим полюсам один или несколько последовательно включенных параллельных резонансных контуров. В результате получают
Р2+*>*
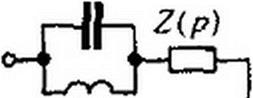
Этот этап соответствует переходу от рис. 10.5. а к 10.5, б.
Коэффициент ак = Res Z3aa(p). Функция Z(p) не имеет полюсов на мнимой оси и p=jwk
представляет собой функцию минимального реактивного сопротивления.
2. Полагая р = j <о, в Z(y о) выделяют действительную часть, т. е. находят ReZ(J а>) и определяют частоту <о, при которой Re = ReZ(y о) — минимальна. Эта частота может быть равна нулю, бесконечности или иметь некоторое конечное значение (в последнем случае ее будем называть о0). Подсчитывают также минимальное значение ReZ(yw), которое называют /?min.
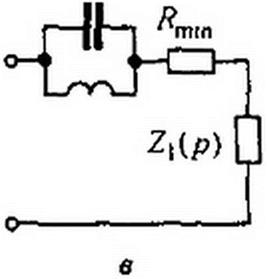
3. Из Z(p) вычитают /?min и находят Z,(p). Этой операции соответствует переход от рис. 10.5, б к 10.5, в. Заметим, что степени числителя и знаменателя Zx(p} одинаковы.
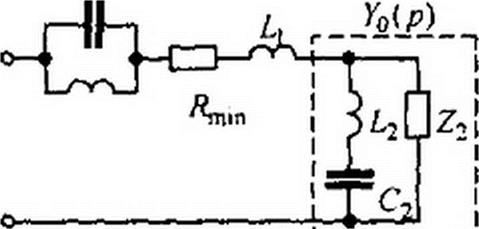
4. Если частота, при которой имеет место минимум RcZ(y (о), равна нулю или бесконечности, то уже на этой стадии делается попытка реализовать Z(p) лестничной схемой. Если же минимум ReZ(y сз) имеет место при некоторой « = соо. отличающейся от 0 и <=о, то дальнейшую реализацию производят в соответствии с п. 5-12.
5. Подсчитывают Z,(p) при р~ j а. Так как при частоте р = у о>о действительная часть Z(p)=/?min, то действительная часть разности Z(y е>0)-J?min равна нулю, т. е. Z|(y<o0) представляет собой чисто реактивное сопротивление j Хх.
6. 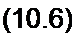 Возможны два случая. Первый, когда А', >0, второй, когда Х{ <0. Будем полагать Х\ =<о0 L\ >0 (случай Х\ <0 рассмотрен в п. 12). Тогда
Возможны два случая. Первый, когда А', >0, второй, когда Х{ <0. Будем полагать Х\ =<о0 L\ >0 (случай Х\ <0 рассмотрен в п. 12). Тогда
= А! /cjq.
 |  | |||||||||||
 | ||||||||||||
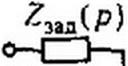 | ||||||||||||
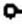 | ||||||||||||
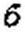 | ||||||||||||
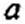 | ||||||||||||
|
 |
д еж
Рис. 10.5
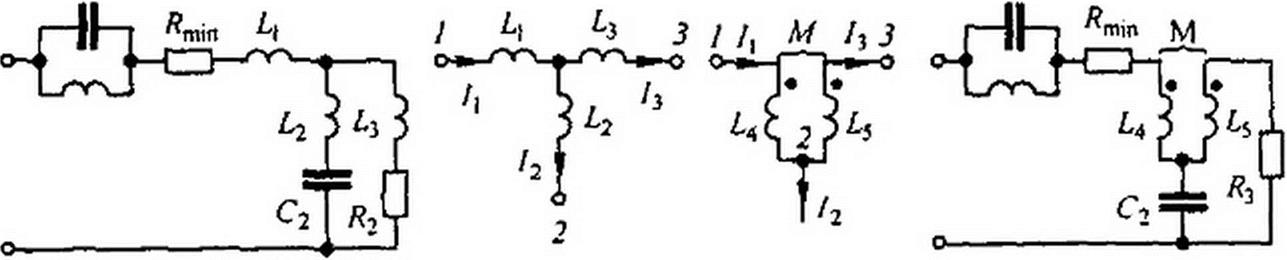
7. Составляют разность Z,(p) - р L( и приводят ее к общему знаменателю. Например, если исходить из того, что
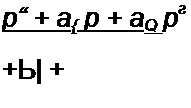 | |||
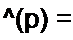 | |||
то проводимость оставшейся для реализации части двухполюсника
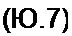 >•«(₽) - 7 ■’ ■----------- = —; .
>•«(₽) - 7 ■’ ■----------- = —; .