Линейным нормированным пространством сигналов называют про­странство, в котором каждому сигналу соответствует свой вектор со своей нормой.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Метрикой двух сигналов f(t) и /?(/) называют норму разности двух сигналов || /(/) - /₂(01|- По метрике можно судить, например, насколько первый сигнал аппроксимирован вторым.

Энергия суммы двух сигналов /(/) + /(/) Р^авна

J(/i(o+/₂w)² <л= ]/²<ол+ {/Лол+2 ]/(₂)/₂(ол.

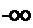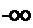00

Величину 2 ]*/(/) fi(f) dt называют взаимной энергией двух сигналов.

Если вещественные сигналы /(/) и /₂(0 имеют спектры S_}(j со) и

S₂ (?<«>)> ^т0 взаимная энергия двух сигналов равна

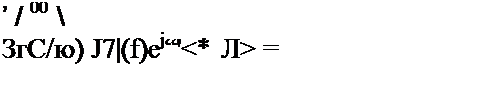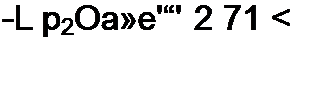— 00

1 ^{+ о}° 1 ⁰⁰

= — js₂(j^ш) ^1(“7 в>) со = — jRe(S₂(y <о) S_{(J со) das. — СО —00

Функцию Re(S₂(./ <*>) 5,(у со) dсо называют взаимным энергетическим спектром двух вещественных сигналов. Взаимная энергия определяется перекрывающимися частями спектров этих сигналов. Формула

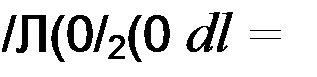
|Re(S₂(/ со) 5](у со) dсо

—СО

получила название обобщенной теоремы Рейли.

Сигналы называют ортогональными, если их взаимная энергия рав­на нулю. Ряд Фурье — пример совокупности ортогональных сигналов.

Т Т

Функции Уолша, принимающие на интервале - —ч-у значения ±1, — второй пример ортогональных сигналов.

Автокорреляционная функция сигнала /(Г) имеет вид

со ад= -СО

Взаимной корреляционной функцией двух сигналов /j(z) и /₂(0 ^на" зывают функцию

со

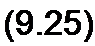Л₁₂(т) = |/|(0/₂('-0</т.

— со

Свойства этих функций рассмотрены в приложении П4, а примене­ние к помехам и дискретным сигналам — в приложениях П4, П5, П7, П8.

Перечислим преимущества цифровых сигналов перед аналоговыми:

1. К шумовым помехам при передаче сигналов полиниям передачи циф­ровой сигнал практически нечувствителен — он либо есть, либо его нет.

2. Цифровой сигнал может передаваться в компрессированном виде, что значительно снижает требуемую для передачи полосу частот, увели­чивает пропускную способность канала передачи и дает возможность передавать по одному каналу несколько компрессированных сигналов от разных источников, если осуществить разделение передачи сигналов по времени.

3. 9.8. Узкополосный и аналитический сигналы. В теории переда­чи сигналов используют понятия узкополосного и аналитического сиг­налов. Узкополосный сигнал занимает узкую полосу частот и может быть представлен как сигнал, у которого во времени медленно изменяется

амплитуда а(г) и фаза <р(/): s(f) - a(t) cos(o)₀ t + (p(t)). Условия медлен- da(t) 1 </<p(0 I

ности изменения: --------------------- « 1 и--------------------------------- « j; где o)_o— опорная

dt ci)q a(f) dt to₀

c7<p(/)

частота, w₀(/) = cd₀ + —-— — мгновенная частота. При обработке узко- dt

полосного сигнала огибающая его воспроизводится амплитудным детек­тором.

Положим, что сигнал s(t) - cos о г, но coswf = — (e^7WZ Таким образом, сиг­

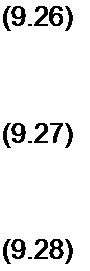
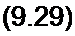нал 5(/) можно представить в виде суммы двух сигналов. Один содержит только положи­тельные, другой только отрицательные частоты. Запишем произвольный сигнал s(t) че­рез его частотный спектр S(j а):

2it ^J 2 it J 2

-x 0

где x

z_v(r) = - p(/©)e>^wZ doi.

⁷¹ о 0

5,(0 = - f-S'U <o)e^yw/ dca\ 71 ^J

-x

c_v(r) соответствует интегрирование при w > 0, ?,(O — при ю < 0.

z_x(t) = s(t) + J s(t)

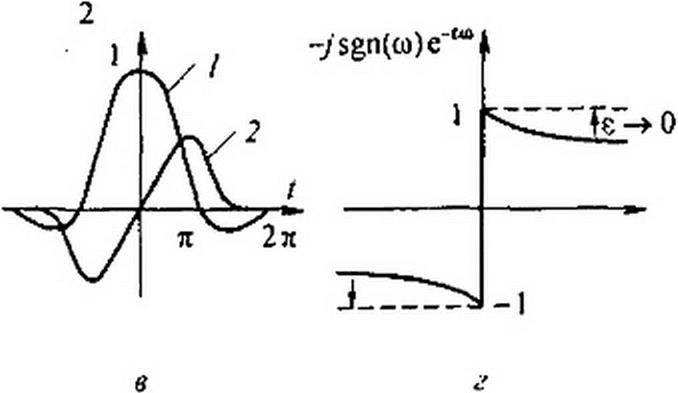
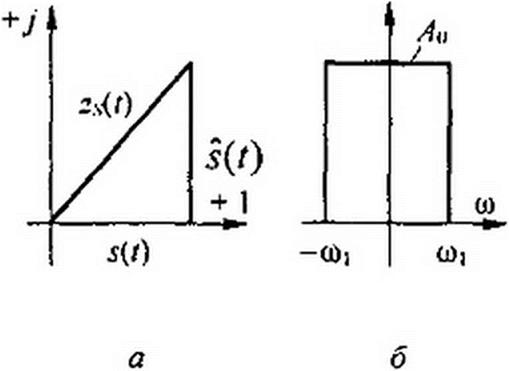
называют аналитическим сигналом, а s(/) = Rez,(O условимся называть исходным сигна­лам. i(/) = lmc,(r) — сопряженным. На комплексной плоскости z_x(t} представляет собой вектор, проекция на ось +1 которого гДО, а на ось +/ = $(/) (рис. 9.5, о). Сигнал z,(/) называют аналитическим потому, что если время t рассматривать как комплексную пере­менную / = /' + >/', то z,(O будет являться аналитической функцией в верхней полуплоскости. Пусть исходный сигнал дДО имеет спектр S(j w) = /!₀ в узкой области частот — от <о = -«I до о) = +«] (узкополосный сигнал рис. 9.5, б). Ему соответствует ана­литический сигнал

Л ^Ш| • А

z_s(t}^ — fe^/tsZ <7(0 = ~ (sin «1, + j ((-COSO, /)).

nJ Kt

0

Исходный временной сигнал s(z) = Rec_v(/) = — кривая I на рис. 9.5, в. Со­

тт О₍ I

1 о, / _w sm" —— пряженный сигнал s(t) = Imz,(г) = —----------- — — кривая 2 на рис. 9.5, в.

7Т (0] Г

Обратим внимание на то, что когда $(г) проходит через максимум, s{t} проходит че­рез нуль.

9.9 . Частотный спектр аналитического сигнала. Так как z_f(l) = s(t) + j s(t), то спектр z_s(t) равен сумме спектров функций $(/) и j s(t), Если спектр $(/) равен S(j о), то спектр s(t) равен

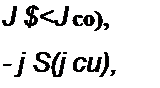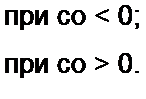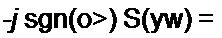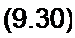Соотношение (9.30) следует из формулы (9.27) и из определения

$(/) = — Г£(;_о)е^' da.

2п ^J

-X

Способ получения s(t) с помощью квадратурного фильтра вытекает из (9.30). На вход этого фильтра подают сигнал $(/). Фильтр, сохраняя модули S{J со) при всех частотах неизменными, изменяет аргументы всех спектральных составляющих на -90° при со > 0 и на +90° при со < 0.

9.10 9.10. Прямое и обратное преобразования Гильберта. Поскольку спектр сопряжен­ного сигнала 5(c) равен S(Jo)= -jsgn(w) S(j<o), то сам сигнал $(/) может быть опре­делен как свертка функций s(/) и некоторой функции времени f(t\ которая определяет­ся по обратному преобразованию Фурье от функции -/sgn(co).

Последнюю представим так:

-y$gn(t))= lim(-ysgn(<o)c ⁽ *) (рис. 9.5,г). С-+О

Тогда 0 /(0^-Z_|im( Г_е^(с*^/О“с/со’ fe⁽’^e+ "^)4> c/cd) = —. (9.31)

2к с-»о • J nt

-ж О

По формуле свертки х

J(/) = l (9.32)

it J i-x

- X

Из (9.30) следует

•S'U со) = j sgn(co) S{j co).

Поэтому, по формуле свертки.

5_(Z) = 1 f (9.33)

Я j X-f
-X

Формулу (9.32) называют формулой прямого, а формулу (9.33) — обратного преоб­разования Гильберта. Для них приняты обозначения Н и Н~¹. Так, s(t) - H{s(t}\ s(j) = H~\s(t)). Ядра подынтегральных функций (9.32) и (9.33) при т = / терпят разрыв, поэтому интегралы следует понимать в смысле главного значения. Например, интеграл (9.32) вычисляют так:

It J f -X J t — x \-X / + Е /

§ 9.11. Вейвлет-преобразование сигналов. Под вейвлет-преобразованием понимают преобразование сигнала /(г) путем воздействия на него малой всплесковой функцией, называемой вейвлет-функцисй —~| (параметры а и Ь которой изменяются во

v а \ Q )

времени), с целью выявления в сигнале низкочастотных и высокочастотных составляю­щих и фиксации времени появления этих составляющих.

Применяют прямое и обратное вейвлет-преобразования. Прямое вейвлет-преобразо­вание позволяет получить вейвлет спектр Wj(a,b} функции /(f):

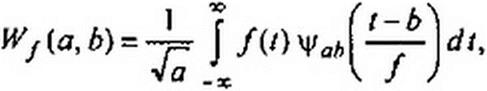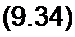а обратное вейвлет преобразование — образовать функцию /(г) по ее вейвлет спектру И>(а. Ь):

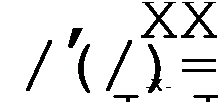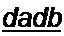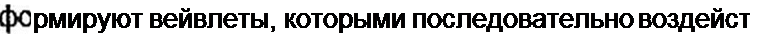X

c_v = ]|ф(ы)||«Г¹ du,
- X

где ф(ф)— преобразование Фурье вейвлета ц>(т); когда норма каждого вейвлета равна 1, C_v = l.

Вейвлет-преобразование применяют к аналоговым и цифровым, к одно- и многомер­ным сигналам.

Под материнским вейвлетом понимают функцию ц/(г), принятую при конкретном вейвлст-прсобразовании. Множитель | 1/а в вейвлет-функции ; устанавли-

da \ a J

васт зависимость нормы вейвлет функции от параметра а. Изменением коэффициентов а

вуют на сигнал /(г), и которые следуют друг за другом при вейвлет преобразовании (9.32).

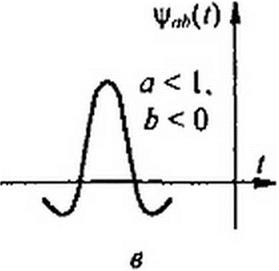
Наиболее распространенным материнским вейвлетом, по международной классифи­кации называемый МНАТ второго порядка, является вейвлет (1-/²)е"' '², являющийся второй производной по времени от функции Гаусса е*' '². Он по форме напоминает мек­сиканскую шляпу (рис. 9.6. а). По сравнению с другими известными типами вейвлет- фуккний он лучше других характеризует сигнал /(/) по времени и частоте.

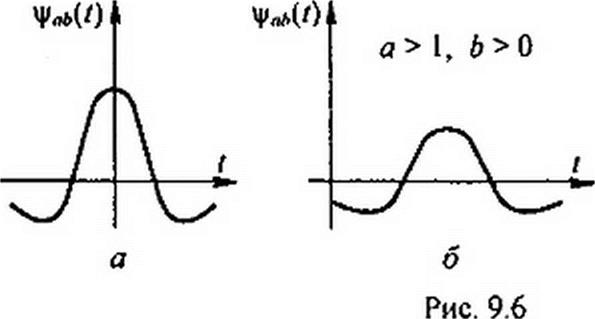
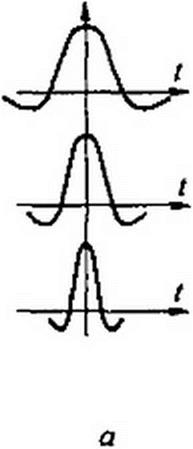
Масштаб во времени функции ч'„/>(<) изменяют коэффициентом а (рис. 9.6, б), сдвиг во времени изменяют коэффициентом b (рис. 9.6, в).

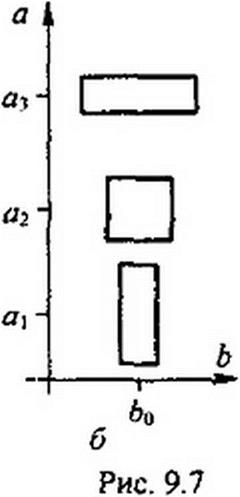
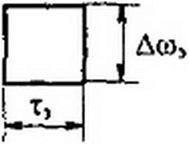
На рис. 9.7, а изображены три функции ^,л(0 с различными значениями коэффици­ента а и различной длительностью импульса. По отношению к каждому из них можно говорить об эффективной длительности импульса т_э и об эффективной ширие соответст­вующей ему части частотного спектра Дш₃. Произведение т_э Дш, (площадь прямоугольни­ка на рис. 9.7, в) характеризует большую часть энергии импульса. Благодаря свойствам самого вейвлета, площади прямоугольников во всех трех случаях, изображенных на рис. 9.7 б, оказываются одинаковыми. При вейвлет-преобразовании (9.34) эти прямоуголь­ники выполняют роль окон, через которые «просматривается» сигнал /(/). Вейвлет-спектр сигнала b) содержит в себе информацию о частотно-временном произведении сиг­нала т₃ Д<о_э, в котором содержится большая часть энергии сигнала. С помощью преоб­разования Фурье получить подобную частотно-временную информацию о случайном сигна­

ле либо затруднительно, либо невозможно, когда сигнал случайный и нестационарный (т. к. вероятностные свойства последнего зависят от момента начала отсчета времени). За это

вейвлет-анализ в литературе иногда называют математическим микроскопом сигнала.

Подробнее о теории вейвлет-лреобразования и его применении в различных областях техники можно узнать из следующих источников: учебного пособия под ред. А.Н. Яков­лева «Радиотехнические цепи и сигналы» (М.: Инфра, 2003), книги В.И. Воробьева и В.Г. Горбушина «Теория и практика вейвлет преобразования» (СПб: ВУС, 1999), статьи В.Г. - Миронова и М.К. Чобану «Состояние и перспективы цифровой обработки многомерных сигналов» (Электричество. 2002. № 11).

Вопросы для самопроверки

1. Чем принципиально отличается ряд Фурье от интеграла Фурье? Запишите и про­комментируйте формулы прямого и обратного преобразования Фурье. 2. Чем объяснить, что при обратном преобразовании Фурье кроме положительной угловой частоты исполь­зуется и отрицательная? 3. Любая ли функция может быть преобразована по Фурье? 4. Для функции /(/) известна Г-'(р). Как записать S(j со) этой функции? 5. Постройте графи­ки модуля и аргумента спектров функций fe~^al и (I - a t) е^-с*'; функции равны нулю при

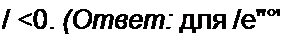2 <о a . , _ ,

—,----- = -arctg—; 7.) 6. Сформулируйте и

^z a'-o’

докажите теорему Рейли, дайте ей физическое толкование. 7. На резистор сопротивлени­ем R = 10 Ом воздействует импульс напряжения, модуль спектра которого S(j о) = 2 Vit при 0 < о < Ю³. В остальной области частот S(w) = 0. Определите энергию, выделившую­ся в резисторе. (Ответ: 400 Дж.) 8. Что понимают под полосой пропускания реального четырехполюсника? 9. Определите полосу частот, занимаемую прямоугольным импу,тьсом длительностью 1 мкс. (Ответ: 6.28 <10⁶ рад/с.) 10. Чем руководствуются при составле­нии укороченных схем четырехполюсника при исследовании деформации фронта и вер­шины проходящего через него короткого импульса? II. Определите текущий спектр 5,(/ а)

функции = полагая, что f(t)-0 при г<0. (Ответ: ---------------------------------------------------------------------------------- .) 12. Про-

1 х a + j

верьте правильность формулы 5{/) = — | cos ш / dt. 13. Покажите, что спектр 5-функции 2 я ^J

равен 1.14. Покажите, что если функция /(/) имеет спектр S(y <о), то спектр функции a f(at) равен S(jo/a). 15. Покажите, что если сигнал $(0 представляет собой ампли- тудно-модулированное колебание О (I + m sin О t) sin о г, то при а » Q сопряженный сигнал s(t) = U (I + т sin Q ) cos w t. 16. Определите автокорреляционную функцию пря­моугольного сигнала /(/). рис. 9.1. в. (Ответ: Я(т) = А~ t„ (1 — Iт]//„).) 17. Определите 2 .j з

энергию и норму сигнала симметричной треугольной формы рис. 8.46, б. (Ответ: у * Ч

и к ,1 —- г: .)

Глава десятая