§ 9.6 Текущий спектр функции времени. За последние годы в литературе стали использовать понятие текущего спектра St(J и) функции времени fit}'.
dt. (9.21)
Формула (9.21) отличается от выражения (9.14) тем, что верхний предел интеграла в ней /, а не «. В соответствии с этим S({j со) является функцией не только й, но и времени /.
Таким образом, ЗДу’й) характеризует спектр в различные моменты времени t. Функция S,(j й) имеет модуль 5(й) и аргумент <рЛ/(й). И модуль, и аргумент текущего спектра видоизменяются по мере увеличения t. Модуль спектра изображают обычно в виде семейства кривых в функции w, каждой из которых соответствует фиксированное время t. Если /(/) — периодическая функция, a t ->оо, то спектр S,(y й) будет дискретным. Если fit}- б при l <0, то текущий спектр определяют по формуле
5,0<о)=/Г(Ое’у"'Л. (9.22)
О
§ 9.7 Основные сведения по теории сигналов. Сигналы подразделяют на детерминированные и случайные. Детерминированный сигнал — это такой сигнал, мгновенное значение которого можно предсказать для любого момента времени. Случайный сигнал — это, как правило, помехи, мешающие получать информацию из принятого сообщения. Импульсный сигнал действует только определенный интервал времени. Сигналы в виде единичных функций l(z), l(-z) и дельта-функция 5(0 рассмотрены в § 8.61. Сигналы в виде модулированных колебаний рассмотрены в § 7.15. Сигнал называют одномерным, если он может быть описан одной функцией времени (например, напряжением на входе цепи).
Сигнал называют многомерным, если он образован совокупностью нескольких одномерных сигналов (например, напряжениями на зажимах многополюсника).
Непрерывный временной сигнал fit} (см. рис. 9.4, а) принято называть аналоговым. Название обусловлено тем, что его можно рассматривать как аналог некоторых физических процессов в рассматриваемом устройстве. Аналоговому сигналу соответствует сигнал в дискретной форме. Дискретные сигналы — это сигналы в виде совокупности следующих друг за другом с интервалом Д дискретных импульсов (см. ри- c. 9.4, б). Ширина каждого импульса одинакова, а площадь равна мгновенному значению сигнала в момент действия импульса.
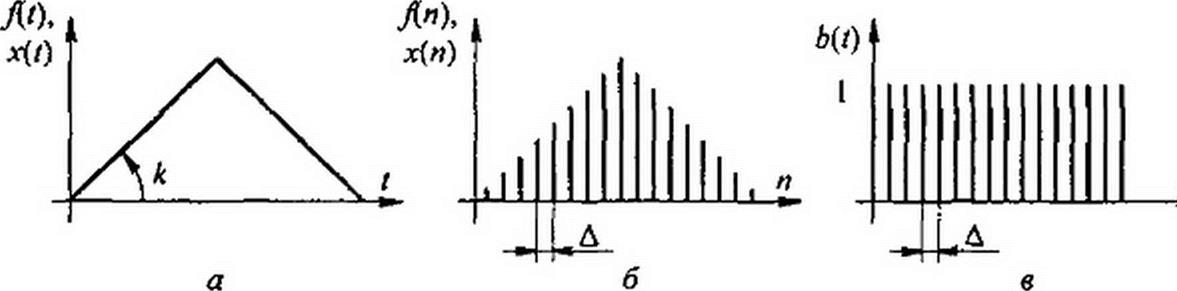 |
|
Цифровой сигнал — это нормированный по уровню дискретный сигнал, представленный в цифровом виде (в двоичной форме записи). Например, 30 = l-24+1-23 +1-22 + 1-21+1-2°->11110. Переход от аналогового сигнала к цифровому осуществляют с помощью аналого-цифрового преобразователя (АЦП), выполненного в виде микросхемы. Обратный переход, с помощью цифроаналогового преобразователя (ЦАП). Обработка цифровых сигналов рассмотрена в приложении П5, а цифровая фильтрация в приложении П7. Сигнал можно рассматривать как вектор в пространстве сигналов. В математике длину вектора принято называть нормой. Квадрат нормы аналогового сигнала//) равен
| /1|2 =f/2(z) Л.
Он характеризует энергию сигнала (см. § 9.4). Энергией сигнала называют энергию, которую сигнал выделяет при воздействии на резистор в 1 Ом. Норма аналогового сигнала
11/11= JfA') Л.
1 -X
Норма не чувствительна к изменению формы сигнала.








