Формулу (8.75) называют интегралом Дюамеля.
С помощью интеграла Дюамеля можно найти не только ток, но и любую другую физическую величину, например напряжение. В этом случае в формулу вместо переходной проводимости g(/) будет входить переходная функция h(t), если на входе цепи действует источник ЭДС
(напряжения), и переходное сопротивление /?(/), если на входе цепи дей ствует источник тока.
§ 8.54 Последовательность расчета с помощью интеграла Дюамеля. Расчет с помощью интеграла Дюамеля проводят в четыре этапа:
1) определение переходной проводимости g(/) (переходной функции А(г)) для исследуемой цепи;
2) нахождение g(/ - т) (Л(/ - т)). С этой целью в формуле для g(t) заменяют / на (/ - т);
3) определение Для этого находят производную от заданного напряжения u(t) по времени /ив полученном выражении заменяют / на т;
4) подстановка найденных на этапах 1-3 функций в формулу (8.75), интегрирование по переменной т и подстановка пределов.
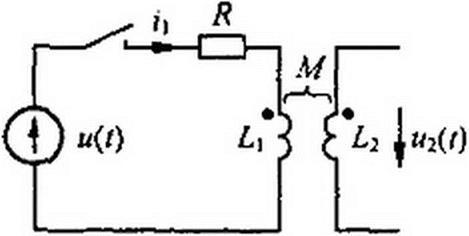
Пример 101. Найти ~ f(i) и и2 = f(t) при замыкании ключа на схеме рис. 8.40. Напряжение источника ЭДС «(/) = 100(1-е-а/) В; а~0,25с~}; Я» 0,5 Ом; /,|=1Гн;
М = 0.5 Гн.
|
Решение. Переходная проводимость цепи, состоящей из последовательно включенных R и L.
g<0 = 1 (j _ Q-h<),
 |
Л
где
 рмуле (8.75) выпадает, так как ц(0) = 0. При этом
рмуле (8.75) выпадает, так как ц(0) = 0. При этом
»'(/) = —100(1-е'я')= 100 о с-я'; dt
ц'(т) = 100ое"ят;
'](/)= р'(т) g{t - т) dx - |е'о: (l-e"A('”:))</t.
• к *
о о
При интегрировании учитываем, что о г г не зависит:
/,(/) = 200 (1 + е’°-5' - 2 е"025') А.
Напряжение на зажимах вторичной обмотки
м2(Г) = м = 50 (е“°-25' - е’°-5') В.
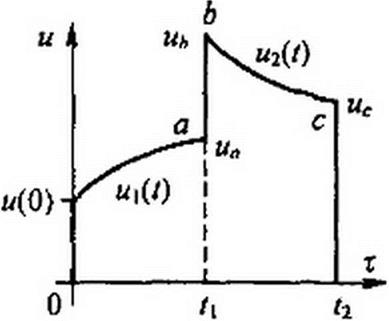
§ 8.55 Применение интеграла Дюамеля при сложной форме напряжения. Пусть напряжение u(t) изменяется во времени по сложному закону, например в соответствии с рис. 8.41. Начальное напряжение равно и(0). В интервале от / = 0 до /=/, напряжение плавно растет, и закон
|
его изменения u^t). В момент t = t} оно меняется скачком от иа до uh, а затем снова изменяется, но уже по другому закону и2 (/) во времени. При t-t2 напряжение скачком уменьшается от ис до нуля.
Требуется найти ток в каждом из трех интервалов времени. Под первым интервалом будем понимать интервал времени от t = 0 до t - z, (не включая скачка напряжения от иа до иь)\ под вторым — от до 12, включая скачок от иа до uhi но не включая скачок от ис до 0; под третьим — при t > t2, включая скачок от ис до 0.
Интегрирование по-прежнему проводим по т, понимая под t фиксированный момент времени, в который требуется найти ток. На основании принципа наложения ток в любой момент времени t определится как сумма токов от всех напряжений, воздействовавших на цепь до момента /.
В первый интервал времени
/(/) = и(0) g(t) + JWj'(t) g(r - г) dx.
о
Во второй интервал времени
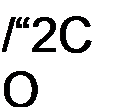 h
h
i(t) = w(0) g(0 + Jw[(t) g(t- t) dx + (uh о
где слагаемое (ub -ua) g(l~/t) обусловлено скачком напряжения от иа и иь в момент времени
В третий интервал времени
/(Г) = w(0) g(t) + Ji/,'(т) g(t - т) dx + (uh - иа) g(t -/j) +
о
'j
+ /«гСО g(/-x)^T + (0-wj g(/-/2)‘
'i
Пример 102. В электрической цепи (см. рис. 8.40) в момент времени / = 0 замы кает - ся ключ и напряжение «(/) изменяется в соответствии с рис. 8.41; и(0) = 50 В. В первый интервал времени от / = 0 до / = /(=4с напряжение w((/) = 150-100е-<,/1, где а = 0,25 с"1. Во второй интервал времени от / = /1=4с до / = /2=6с и2(/) = 50 + 100е"с('_/|), где с = 0.4с'1. Параметры схемы (см. рис. 8.40) /? = 0,5Ом; L] = I Гн (вторичная цепь разомкнута).
Найти закон изменения тока во времени для обоих интервалов времени, а также значения тока it при г, равном 2 и 5 с.
Решение. В соответствии с § 8.54 переходная проводимость
g(f) = 1 (1 “ е’*'); b = у = 0.5 с"1; g(t - т) = ~ (1 - е-А(/’т))-
К L к
В первый интервал времени и'(т) = 100 се'"1. Поэтому
/| (О = «(0) g(/) + jw'(T) g(t - х) dx =
о
= + [е'"т(1-е'А(,-т))<Уг =
R R *
о
= I00(!-e-0>s') + 200(l + e’°-s' -e'025').
Приг = 2 c /, = l00(l-e”l) + 200(l + e"1-2e-0,5) = 94,9 A.
Во второй интервал времени (включая скачок иь - иа = 36,9 В )
Ъ /
'1(0 = и(0) g(/) + Jw[(r) g(t - т) dx + (uh - u„) g(i J«2(T) g(t ~x)dx\
0 'I
^(т) = -Ю0се‘‘гсс'1;
/, U) = 100 (I - e '°-5') + 200 (0,632 - 1.718 e -A5') + (1 - e'03 >) -
0 j 5
—e’c' +Az£c-‘'i +e"c'i c-c('-'i))e-<'».
(b-c)R с c
При I = 5 c /) = 204.32 A.
§ 8.56 Сравнение различных методов расчета переходных процессов. Классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться, во многом зависит от навыка и привычки.
Однако классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано.
Если при сравнении методов исходить из объема вычислительной работы, то решение уравнений первого, второго, а иногда и третьего порядков для источников постоянной (синусоидальной) ЭДС или тока целесообразно проводить классическим методом, а решение уравнений более высоких порядков — операторным. Объясняется это тем, что чем выше порядок характеристического уравнения, тем более громоздкой и трудоемкой оказывается операция нахождения постоянных интегрирования в классическом методе. Операторный метод имеет перед классическим явное преимущество при решении задач, в которых определение принужденной компоненты искомой величины оказывается затруднительным вследствие сложного характера вынуждающей силы, а также при решении уравнений в частных производных (см. § 12.13-12.15). Если воздействующее напряжение изменяется во времени, например линейно или в виде всплеска одной или нескольких экспонент, рекомендуется применять операторный метод или интеграл Дюамеля. Но основной областью применения интеграла Дюамеля являются случаи, когда напряжение изменяется по сложному закону во времени, например при наличии скачков напряжения (см. § 8.55), или когда переходная проводимость g(r) и (или) воздействующее на схему напряжение заданы графически
(в последнем случае интеграл Дюамеля берется путем численного интегрирования).
Рассматриваемый в § 8.66 метод расчета переходных процессов, получивший название метода пространства состояний, используется главным образом, когда расчет осуществляется с применением ЭВМ. Для ручного счета этот метод громоздок.
Классический и операторный методы, а также метод пространства состояний в аналитической форме и интеграл Дюамеля имеют общий недостаток: необходимость определения всех корней характеристического уравнения, что для уравнений высоких степеней (например, 5-, 6-, 7-й, ...) требует много времени. В этих случаях может быть рекомендовано числовое решение на ЭВМ уравнений, составленных по методу пространства состояний; может быть применен и спектральный метод в том виде, в каком он рассмотрен, например, в гл. 9. Кроме того, в этих случаях используют моделирующие установки.
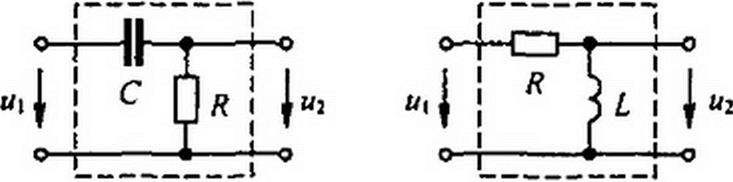
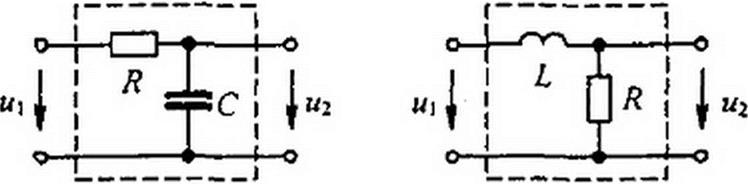
§ 8.57 Дифференцирование электрическим путем. Для четырехполюсников (рис. 8.42) при определенных условиях выходное напряжение и2(/) пропорционально производной от входного напряжения ^(Г),
 |
|
т. е. м2(/)« dux(f)ldt. Схему на рис. 8.42, а применяют чаще схемы на рис. 8.42, б, так как при практическом осуществлении она обладает меньшими габаритами, массой и более удобна при регулировке.
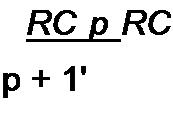 Если u}(t)=U}(p), то du\(t)/dt = р Отсюда следует, что четырехполюсник осуществляет дифференцирование, если для него
Если u}(t)=U}(p), то du\(t)/dt = р Отсюда следует, что четырехполюсник осуществляет дифференцирование, если для него
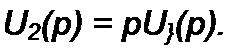 Для схемы на рис. 8.42, а 6/2(р) " Ц(р)
Для схемы на рис. 8.42, а 6/2(р) " Ц(р)
Чтобы схема осуществила дифференцирование, необходимо выполнить условие | Л С р |« 1, тогда t/2(p)« RC р Ц(р). Для синусоидального процесса заменим р на j со и тогда схема на рис. 8.42, а будет выполнять свои функции, если со RC « I.
Аналогично доказывается, что для схемы на рис. 8.42, б необходимо выполнить условие (со L/ R) « 1. Если ux(t) — несинусоидальная периодическая функция, то эти условия должны выполняться для наивысшей частоты функции Wj(z).
При дифференцировании импульсных воздействий длительностью /н параметры схем на рис. 8.42 должны удовлетворять условиям RC « tH и L!R « гн. Эти условия получим из двух предыдущих, если в первом приближении будем считать, что поступление на вход четырехполюсни
ка импульса длительностью гн соответствует воздействию на вход одной полуволны синусоиды частотой (о = 2л/(2/н) = л:/гн.
§ 8,58. Интегрирование электрическим путем. Для четырехполюс
ников (рис. 8.43) при определенных условиях выходное напряжение
 |
| ||||
| ||||
Схема на рис. 8.43, а предпочтительнее схемы на рис. 8.43, б по причинам, упомянутым в § 8.57.
Если то р](г) р' Отсюда следует, что схема
выполняет свои функции, если соотношение между ее параметрами обеспечивает выполнение соотношения (У2(/?) = U\{pVР-
JXnn схемы на рис. 8.43, a U2(p') = Ux(p')/(R С р +1), т. е. для нее должно быть | R С р | » 1. Заменив р на j со, найдем условие w R С » 1, при котором схема на рис. 8.43, а будет выполнять функции интегрирующего звена при синусоидальном процессе. Для схемы на рис. 8.43, б со Ы R » 1.
При интегрировании импульсных воздействий длительностью zH должны быть выполнены следующие условия: /?С»гн для схемы на рис. 8.43, а и L/ R » tH для схемы на рис. 8.43, б.
Напряжение с выхода интегрирующего (дифференцирующего) устройства подается для наблюдения (записи) на электронный осциллограф.
§ 8.59 Передаточная функция четырехполюсника на комплексной частоте. Под передаточной функцией четырехполюсника К(р) на комплексной частоте р понимают отношение выходного напряжения 4/2(р) ко входному U\(p} (рис. 8.44, а):
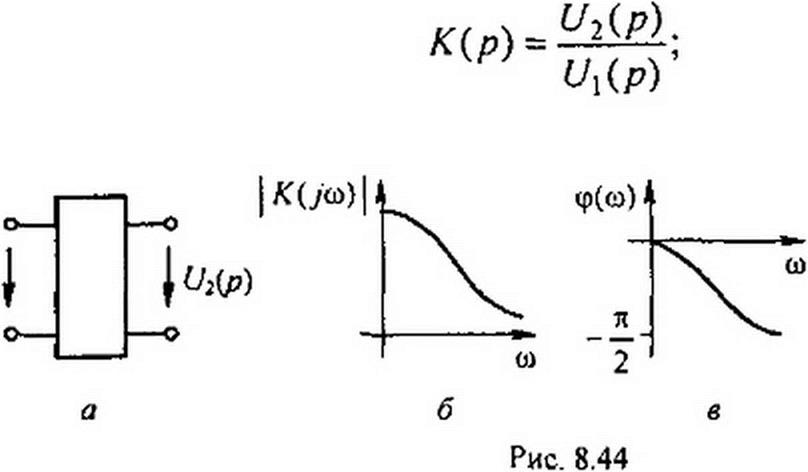 | |||||
 | |||||
 | |||||
К(р) зависит от схемы четырехполюсника, числового значения элементов схемы и от частоты р. Для четырехполюсника (рис. 8.43, б)
К(р) =------------- . Из уравнения (8.76) следует, что
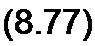 R + р L
R + р L
U2(p) = K(p)U}(p).
Под передаточной функцией четырехполюсника для синусоидального процесса на частоте со понимают отношение
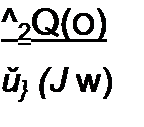 | |||||
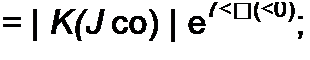 | |||||
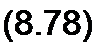 | |||||
X'(yco) получают из K(p) заменой р на у со, |/С(усо)|— модуль, а
ср(со)— аргумент K(j со). Для схемы на рис. 8.43, б K(j со) ------------------------------------------- ------------------------------------------------------------- -
ср(со) = arctg
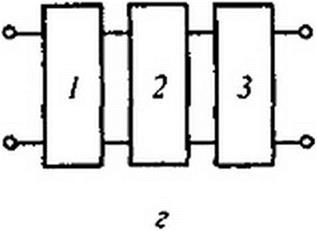
Зависимости | K(J со) и ф(со) изображены на рис. 8.44, б, в. Если не-
сколько четырехполюсников, например три, соединены каскадно (рис. 8.44, г) и известны передаточные функции каждого четырехполюсника, то передаточная функция каскада в соответствии с формулой (8.77) равна произведению передаточных функций этих четырехполюсников:
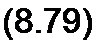 | |||
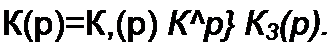 | |||
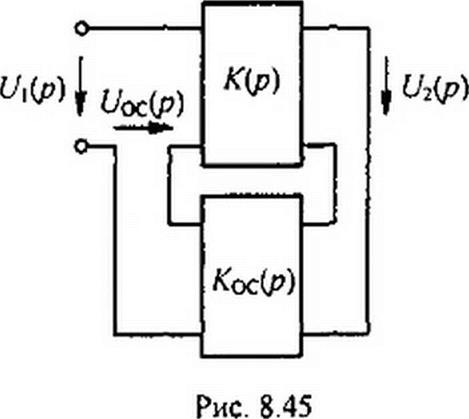
Пример 103. На рис. 8.45 изображена замкнутая система (система с обратной связью). Она состоит из основного четырехполюсника с передаточной функцией К(р) и четырехполюсника обратной связи с Кос(р) Функцию последнего часто выполняет усилитель, работающий в режиме пропорционального усиления. Вывести формулу передаточной функции всей системы Кзс(р).
Решение. На вход основного четырехполюсника поступает основной сигнал G't(p) и сигнал с выхода четырехполюсника обратной связи, поэтому
U2(p) = (U](p)±Uoc(p))K(p). (8.80)
Кроме того,
Uoc(P>= Koc(p)U2(p). (8 81)
Подставим (8.81) в (8.80). Получим
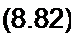 Л. (Р) —--------- — —-------------------------
Л. (Р) —--------- — —-------------------------
и^р) \±К{р)Кос(р)
Если 1 - К(р) КО(:(р) = 0, то в системе возникнут автоколебания, амплитуда их будет ограничиваться нелинейностью системы. Плюс в формуле (8.80) и минус в формуле (8.82) соответствуют положительной обратной связи. Минус в формуле (8.80) и плюс в (8.82) — отрицательной.
§ 8.60 Переходные процессы при воздействии импульсов напряжения. Ток в любой схеме при действии на нее импульса напряжения (ри- c. 8.46, а) можно найти, например, тремя способами:
1) применяя интеграл Дюамеля;
2) определяя ток при t <t} так же, как от действия постоянного напряжения £/; при t < Zj действующее на систему напряжение равно нулю. Следовательно, система освобождается от вынуждающих ЭДС и по ней протекают свободные токи, обусловленные запасом энергии в индуктивных и емкостных элементах системы;
3) представляя импульс в виде двух постоянных напряжений. Положительное напряжение U действует начиная с t = 0, отрицательное — начиная с / = При t < токи в цепи определяются одним напряжением U\ при i > Zj — обоими напряжениями с учетом сдвига второго напряжения на время
и к
Рис. 8.46
Рассмотрим третий способ. Положим, что требуется найти ток в цепи при подключении ее к источнику напряжения, имеющего форму равнобедренного треугольника (рис. 8.46, б). Задача решается в три приема.
Сначала определяем ток в интервале времени от / = 0 до Z</| от действия напряжения щ - к / (рис. 8.46, в). Затем для интервала времени l2 находим ток в цепи от действия двух напряжений (рис. 8.46, в, г): от продолжающего действовать напряжения = к t и от вступающего в действие при t -tx дополнительного напряжения и2 = —2 к (t —).
Для интервала времени / > t2 ток определяется действием трех напряжений: продолжающих действовать напряжений щ и и2 и вновь вступающего в действие при t =t2 напряжения и2 - к (I -t2) (при t >t2 сумма напряжений wb и2 и иу (рис. 8.46, д) даст нуль).
Из трех перечисленных способов наиболее экономным является первый.
При воздействии серий импульсов переходный процесс рассчитывают часто операторным методом.
Пример 104. На последовательно соединенные R и L поступает серия прямоугольных импульсов напряжения единичной амплитуды; длительность импульса х и длительность паузы также т (рис. 8.46, е). Используя третий способ в сочетании с теоремой запаздывания (см. § 8.40), определить ток в цепи.
Решение. Найдем изображение напряжения:
t/(p) = l(l-e-^ +е-2^-е’3рт + ...).
Р
Выражение в скобках представляет собой бесконечную геометрическую прогрессию со знаменателем — е"7”. Сумма членов ее равна ——- -—. Изображение тока
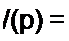 | |||
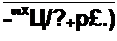 | |||
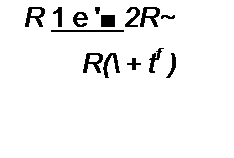
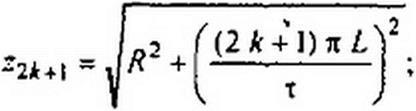 | |||
 | |||
Применим формулу разложения. Корни знаменателя:
р' = 0; p‘ = -R!L\ х Pt ={ak + J Ь^)х = j п(2 к+ 1) (-a> <£<<»).
Группируя член к=0 с к--\. член А = ] с членом к = -2 и т. д., получим
х $in(n(2fc + 1)--Ф2* + |)
+-Z--------------------------- —
Л *=0 *2[§] [**]1
| (ад -Ат / 2 |
| dt равна единице. Единицей измерения 8-функции |
| является се |
кунда в минус первой степени. Если импульс действует при некотором
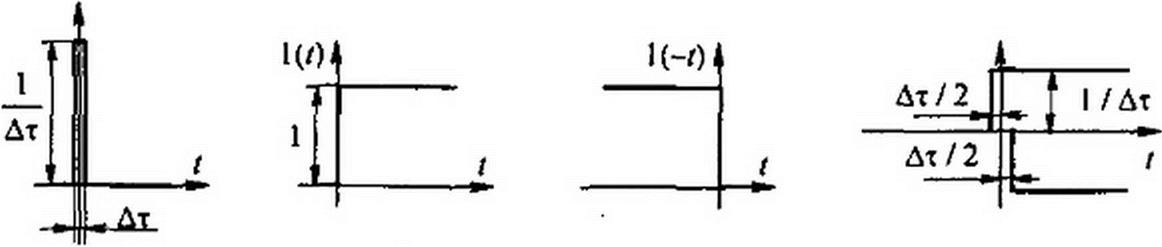 |
|
времени t = /1} то он обозначается как 50* - б), т. е. импульс действует, когда аргумент 5-функции равен нулю.
Единичной функцией 1(/) (рис. 8.47, б) называют функцию, равную единице при />0 и равную 0 при /<0. Единичной функцией ](-/) (рис. 8.47, в) называют функцию, равную 1 при t <0 и равную 0 при Г>0. Функции 1(г) и 1(-г) имеют нулевую размерность. Рассмотрим свойства перечисленных функций:
— производная по времени функция !(/) равна S-функции, т. е.
®
at
5-функция обладает фильтрующим действием:
f^^t-t.^f^b^t-t^
— изображение 5-функции по Лапласу равно единице: а изображение функции 5(f - ) на основании теоремы смещения равно е“р/‘;
 |
| |||
| |||
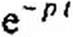 |
|
— единичные функции 1(/) и 1(-/) также обладают фильтрующим действием.
Умножение произвольной функции /(/) на ](/) обращает произведение f(t) 1(г) в f(t) при />0 и в нуль при / < 0. Аналогично произведение /(/)!(-/) обращается в нуль при />0 ив /(г) при 1<0. Импульсное (игольчатое) напряжение или ток в виде 5-функций единичной площади записывают так: 5(/) • 1. Здесь единица имеет размерность вольт- секунда или ампер-секунда соответственно.
Если на электрическую цепь, входная проводимость которой равна g(/), при нулевых начальных условиях воздействует единичный импульс напряжения 5(/)-1 Вс (рис. 8.47, а), то для определения вызванного им тока в цепи представим импульс в виде двух прямоугольных напряжений (положительного и отрицательного) с одинаковыми числовыми значениями ] / Дт, сдвинутых во времени на величину Дт -> 0 (рис. 8.47, г).
Ток в цепи после окончания действия импульса
>(О = 4- (g(r + Дт / 2) - g(Z - Дт / 2)).
Дт
Разложим функции £(/ + Дт/2) и £(г-Дт/2) в ряд Тейлора по степеням Дт/2, учтем малость Дт и получим
'■(О=4" («(')+г'(') - 8(0+-V = I ■«’(/).
Дт у 2 2 J
Здесь и далее 1 имеет размерность Вс.
Величину g'(/) = называют импульсной переходной проводимо- d t
стью. При />Дт (Дт-»0) g'(0» умноженная на 1 Вс, численно равна току в цепи при воздействии на нее единичного импульса напряжения
 $(/)•! Вс. Аналогично величину /?*(/) =
$(/)•! Вс. Аналогично величину /?*(/) =
 переходной функцией четырехполюсника. При t > Дт (Дт неженная на 1 Вс, численно равна напряжению на выходе четырехполюсника при воздействии на его вход единичного импульса напряжения 5(/) • 1 В с. В интервале времени от / = -Дт / 2 до / = Дт / 2 (во время действия импульса 5(z)l Вс) напряжение на выходе четырехполюсника
переходной функцией четырехполюсника. При t > Дт (Дт неженная на 1 Вс, численно равна напряжению на выходе четырехполюсника при воздействии на его вход единичного импульса напряжения 5(/) • 1 В с. В интервале времени от / = -Дт / 2 до / = Дт / 2 (во время действия импульса 5(z)l Вс) напряжение на выходе четырехполюсника
и2(О = Л(0)б(/)-1 + Л'(О-1,
а ток на входе двухполюсника
/(/) = g(0) 6(0 • 1 + g'(0 • 1 •
Наряду с понятиями «переходная проводимость» g(0 и «импульсная переходная проводимость» g'(f) применяют дуальные им понятия: переходное сопротивление г(Г) и импульсное переходное сопротивление Переходное сопротивление rafr(z) численно равно напряжению на входе цепи uQh(t) при воздействии на ее вход единичного тока:
"«л(О = Ц^)^(О.
Импульсное переходное сопротивление rj5(z) численно равно напряжению на входе цепи uaf)(t), после того как на ее вход воздействовал импульс тока в виде 5-функции единичной площади:
uuh(0 = 5(0- 1(А с)-г'аЬ(1).
Величины r(z) и r'(t) могут быть входными и взаимными, однако g(t) и R(t) не являются взаимно-обратными величинами; g(z) определяется при питании схемы от источника ЭДС, а Я(/) — при питании схемы от источника тока.
Подчеркнем, что в литературе по переходным процессам в зависимости от рассматриваемого вопроса под одним и тем же названием — импульсная переходная функция — понимают функцию либо либо A5(z). Между этими функциями имеется зависимость
Л5(/) = Л(0,)6(0 + Л'0);
Л'(/) характеризует реакцию четырехполюсника (его выходное напряжение) после окончания воздействия на его вход единичным импульсом напряжения l-5(z)B-c, а /?5(z) —напряжение на выходе четырехполюсника и во время действия импульса, и после окончания.
Аналогичные соотношения существуют между двумя импульсными переходными проводимостями:
| s5W=g(ot)S(o+g'(/) |
| и между двумя импульсными переходными сопротивлениями: |
| Л5(/) = Я(0ф)8(г) + Ш |
| при воздействии на вход схемы единичным импульсом тока. С помощью h5(t) интеграл Дюамеля запишется так: |
| «г(0 = |“(^)Л8(/-т) с/т. |
| Здесь Л 5 (/-?) = Л(0) 5(г - т) + h'(J - т). |
| Формулу интеграла Дюамеля в математических работах называют формулой свертки двух функций, в данном случае функций г/(/) и As(z). |
| § 8.62. Определение h{t) и А6(/) через К{р). Как упоминалось, при воздействии на вход четырехполюсника единичного напряжения «((/) = ](/) напряжение на выходе его u2(t) = h(t). Если это положение записать относительно изображений, учитывая, что !(/) = —- и обозначив р изображение Л(/) через Н(р\ то Н(р') = К(р)/р. Отсюда |
| К(р) = р Н{р). |
| (8.83) |
| Определим теперь Л(/) через К(р). Поскольку h(t)^H(p\ а Н(р') определено предыдущей строкой, то |
| (8.84) |
| При воздействии на вход четырехполюсника единичным импульсом напряжения ut(f)- 1 ♦§(/) = ] =щ(р) напряжение на выходе его |
| «2(о=/>8(о=<адад=1-ад, таким образом, |
| *5(0=ад- |
| (8.85) |
| Пример 105. Запишем h(t\ hb(t) для схемы на рис. 8.42, а. |
| hb(t)=K(p) = |
| ПС |
.63. Метод пространства состояний. Метод пространства состояний (метод переменных состояния) представляет собой упорядоченный способ нахождения состояния системы в функции времени, использующий матричный метод решения системы дифференциальных уравнений первого порядка, записанных в форме Коши (в нормальной форме). Применительно к электрическим цепям под переменными состояния понимают величины, определяющие энергетическое состояние цепи, т. е. токи через индуктивные элементы и напряжения на конденсаторах. Значения этих величин полагаем известными к началу процесса. Переменные состояния в обобщенном смысле назовем х. Так как это некоторые функции времени, то их можно обозначить х(Г).
Пусть в системе п переменных состояния. Матрицу-столбец переменных состояния в n-мерном пространстве состояний обозначим [х] = т выходных величин (токи, напряжения) обозначим у, матрицу-столбец
У]
выходных величин [у] =
L-M
Источники воздействий (источники ЭДС и тока) будем именовать z.
Матрица-столбец источников воздействий [z] =
Для электрических цепей можно составить матричные уравнения вида
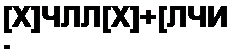 | |||
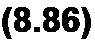 | |||
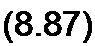 [у] = И И+[0] И»
[у] = И И+[0] И»
где [Л/], (/V], [Р], [£>] — некоторые матрицы, определяемые структурой цепи и значениями ее параметров.
На основании принципа наложения решение (8.86)
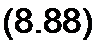 [x(r)] = eIM,f [х(0)]+ |е(ЛУ]и’т) [W][z(t)J dx,
[x(r)] = eIM,f [х(0)]+ |е(ЛУ]и’т) [W][z(t)J dx,
о
где (х(0)]— матрица начальных значений х.
Первое слагаемое в формуле (8.88) описывает свободные процессы в системе, второе — принужденные и свободные при нулевом исходном состоянии (вывод формулы (8.88) см. в конце параграфа).
Из (8.87) и (8.88) находим
МО) = И е'"1' МО)] + j[P] e|M l('-”[W] [z(t)] dt + [Q] [z(/)J. (8.89)
0
|
Систему уравнений 8.86 составляют либо на основании законов Кирхгофа, либо путем приведения схемы к резистивной (без элементов L и С). Как это можно сделать, пояснено в примере 100.
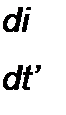 | |||||
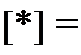 | |||||
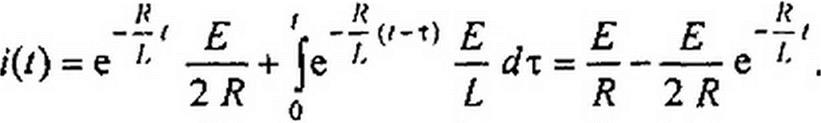 | |||||
|
Поясним формулу (8.88) на простом примере. Ток в схеме на рис. 8.48 до коммутации был /(0_) = Е/(2 Я). Уравнение состояния для этой схемы dildi = -(Я/L) i + (Е/Е), т. е.
Матричную функцию e^' в формуле (8.88) вычисляют по формуле (теореме) Сильвестра:
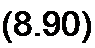
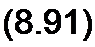 =e^^j1] + e^/ [^l + .^ + e’1"' [Л„],
=e^^j1] + e^/ [^l + .^ + e’1"' [Л„],
где
п in
[Л]=П(["]-Х>[Ч) /1Ж-Ъ);
7 = 1 / 7-1
f г
Здесь Хг— собственные значения (характеристические числа) квадратной матрицы [Л/], т. е. корни уравнения
det([A/]-X[i]) = 0. (8.92)
Из уравнения (8.92) следует, что уравнение относительно X составляют, приравнивая к нулю определитель матрицы [М], в котором все элементы этой матрицы атт(т = I,..., и), расположенные по главной диагонали, заменяют на элементы атт -X.
Характеристические числа X— это не что иное, как корни характеристического уравнения послекоммутационной схемы. Запись решения в виде ряда (8.90) предполагает, что все характеристические числа различны (нет кратных корней).
Если же среди корней уравнения det([A/]-X[l]) = 0 будет кратный корень X, кратности 5, то составляющая е^', обусловленная этим корнем, имеет вид
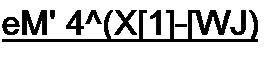 | |||||
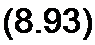 | |||||
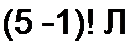 | |||||
где A dj (Х[1]-[Л/])— присоединенная матрица к матрице Х[1}-[Л/]. В ней все элементы заменены на алгебраические дополнения, а затем проведено транспонирование. Составляющие решения по формуле (8.93) соответствуют части решения по формуле разложения (см. § 8.50), учитывающей кратные корни.
При машинном счете функцию е^', подсчитывают разложением в ряд:
е1"1' =[1] + [М]; + ^ЦД- + ....
3.
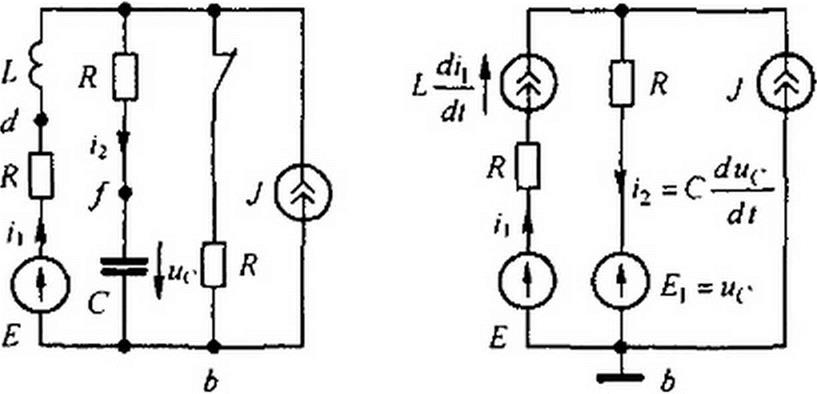
Пример 106. Методом пространства состояний исследовать переходный процесс в схеме на рис. 8.49, а. До коммутации был установившийся режим:Е = 4В; J = 1 А; К = 2 Ом; Л = 1Гн; С = 1 Ф.
Решение. Обозначим токи и напряжения в соответствии с рис. 8.49, а. До коммутации
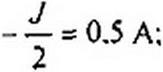 | |||
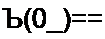 | |||
|
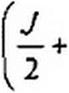 |
| |||
| |||
В качестве переменных состояний выбираем ток /( и напряжение на конденсаторе и(-.
Известно несколько способов составления уравнений состояния. Рассмотрим иногда применяемый, основанный на сведении послекоммутационной схемы к резистивной с источниками ЭДС и тока. С этой целью индуктивные элементы в послекоммутационной схеме заменяем на источники тока, которые доставляют ток в том же направлении, что и в исходной схеме (в рассматриваемом примере L заменяем на источник тока ij с напряжением на нем L di} Idt), а конденсатор С — на источник ЭДС, причем в соответствии с теоремой компенсации ЭДС этого источника должна быть направлена встречно току в ветви с конденсатором, т. е. встречно напряжению на конденсаторе (в рассматриваемом примере конденсатор С с напряжением на нем ис заменен на источник ЭДС Е) =и(-).
В результате схема окажется без индуктивных и емкостных элементов (чисто резистивной). но с дополнительными источниками тока и ЭДС (рис. 8.49. б).
 |
|
а б
Рис. 8.49
В полученной резистивной схеме один из узлов заземлим. Составим уравнения по методу узловых потенциалов и определим потенциалы незаземленных узлов. В рассмат* риваемом примере не заземлен всего один узел а. Поэтому
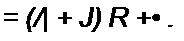 | |||
 | |||
По известным потенциалам узлов рассчитаем напряжения на источниках тока Lkdikldt эквивалентируюших индуктивные элементы Lk, и токи im=C„duCmldt через источники ЭДС, эквивалентирующие емкостные элементы емкостью Ст.
Для первой ветви схемы на рис. 8.49, б
Фа = (/! + J) Я + = £ -> /( R~ L ■
dt
Отсюда
di, 2 R . и/- Е R
—L ---------- f _ _s_ +-----
dt L ' L L L
Ток второй ветви i2 можно определить по первому закону Кирхгофа или по закону Ома для участка цели с источником ЭДС:
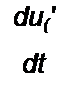 ^а~ис <i}+J)R + uc-uc
^а~ис <i}+J)R + uc-uc
R R
Следовательно,
du(-/ dt = (ц/С) + (J/С).
Таким образом, уравнения переменных состояния для послекоммутаиионной схемы на рис. 8.49, а таковы:
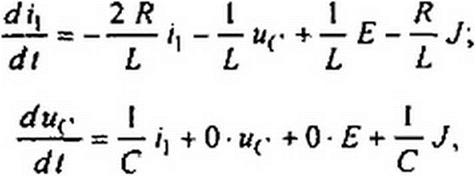 |
 | |||||
 | |||||
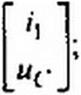 | |||||
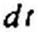 | |||
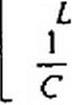 | |||
|
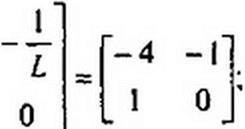 | |||||||||
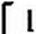 | 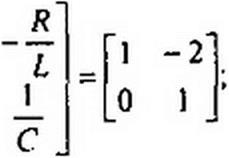 | ||||||||
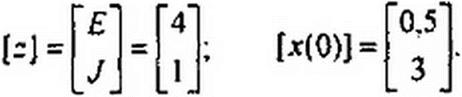 | |||||||||
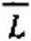 | |||||||||
Составим уравнение для определения характеристических чисел X:
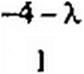 |
Таким образом.
2?+4Х + 1 = 0; Л|=-0,27; Х2 = -3,73с“‘.
По формуле (8.91),
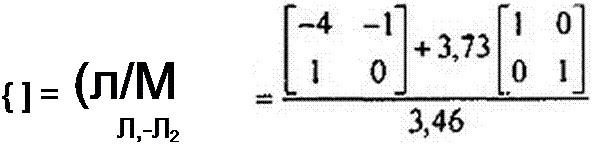 |
|
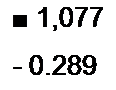 | 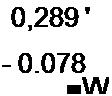 | ||||
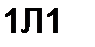 | |||||
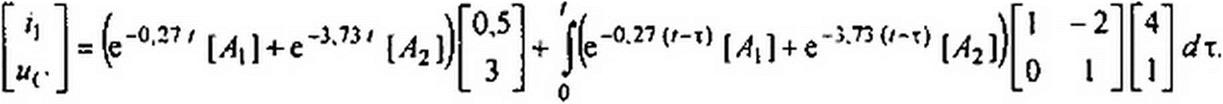 |
|
Выполнив подсчеты, получим
/j =-1+0,75 е'027' +0.75 е-3'73' Л:
ие = 6-2.8е“°-27/-0,2е-3,73' В.
Если за выходную величину^ принять напряжение между точками d и/, то
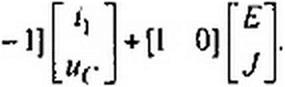 |
|
 | ||||||||||||||
 | ||||||||||||||
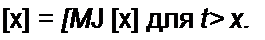 | ||||||||||||||
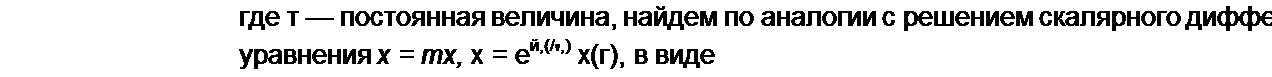 | ||||||||||||||
 | ||||||||||||||
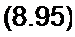 | ||||||||||||||
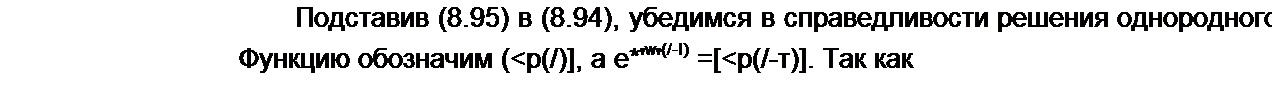 | ||||||||||||||
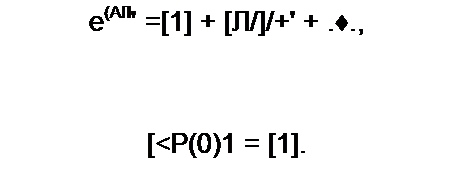 | ||||||||||||||
 | ||||||||||||||
В соответствии с методом вариации произвольных постоянных частное решение неоднородного уравнения представим в виде
[хч(/)] = [<р(/-т)] [«(/)] (х(т)].
Общее решение
[х(П] = [Ф(/ - т)] [x(t)J + [Ф(/ - г)] [«(/)] (х(/)] =
= [ф(/ - т)] (1] + [»(/)] [х(т)] = [<р(/ - т)] [Л(0],
где Л(г) требуется определить.
Подставим
(х(г)] = [ф(/ - т)1 {/?(/)] (8.96)
в уравнение (8.86):
((<i>0 - t)J - [М ] [Ф(г - т)]) (Я(Г)] + [Ф(/ - т)] (Я(/)] = [.л/] [z]. (897)
Поскольку (<р(/-т)| есть матрица, столбцы которой являются решением уравнения (8.94), то первый член выражения (8.97) — нулевая матрица. Следовательно.
(ад = [<р(/-т)Г1 bVH-J (898)
Проинтегрируем (8.98) от т до/:
(/?(/)]-[ВД]= /[ф(Х-т)Г? [.VjUJrfk. (8.99)
т
Из уравнений (8.96) и (8.99) следует
[Ф(/ - т)Г' КО] = (Ф(О)Г' (х(т)] + |(<р(Х - т)]'1 [;V][z(X)J d\, (8.100)
X
но [ф(0)} = [1]. Умножая (8.100) слева на [<р(/ - т)] и учитывая, что
[ф(/-т)Нф('-т)Г’ =е[Л/1('-,) e'(W](Vtl =е1Л/](,-М
получим
[х(/)) = [ф(/-т)][х(т)1+ |[ф(Х-т)ЦУ)(с(Х)]агХ. (8.101)
X
Полагая в (8.101) т = 0 и заменяя затем переменную X на т, получим формулу (8.88).
§ 8.64 Дополняющие двухполюсники. Два двухполюсника, содержащие элементы R, L, С, называют дополняющими, если входное сопротивление при их последовательном (параллельном) соединении оказывается чисто активным, не зависящим от комплексной частоты р. Так, двухполюсник из параллельно соединенных L и R2 и двухполюсник из параллельно соединенных С и R} (рис. 8.50, а) являются дополняющими при их последовательном соединении и выполнении условия
r]=r2=r = /l i с.
 |
|
Двухполюсники Я2, Си Л,, L при их параллельном соединении (рис. 8.50, б) являются дополняющими при том же условии.
Элементы двух дополняющих двухполюсников взаимно-дуальны. Элементам С,, /?! одного соответствуют такие дуальные элементы С2, L2, Я2 дополняющего, что произведение сопротивлений двух взаимно дуальных элементов должно быть равно R2, где R — произвольное активное сопротивление.
Последовательное соединение и С} в исходном двухполюснике заменяют на параллельное соединение С2 = Ц/ R2 и L2 = Q R2 0 дополняющем.
Параллельное соединение С] и Д, в исходном двухполюснике заменяют на последовательное соединение L2 = С( R2 и С2 = L^l R2 в дополняющем.
§ 8.65 Системные функции и понятие о видах чувствительности. Системные функции Н(р) — это обобщенное название функций, характеризующих четырехполюсник. Ими могут быть, например, передаточная функция напряжения U2(p)IU\(p), передаточная функция тока /2(р)/ АС/7) и т. п. Если какой-либо параметр (Я, L, С) в схеме четырехполюсника изменяется, то изменяются модуль и аргумент системной функции и можно говорить о чувствительности системной функции к изменению этого параметра.
Под классической чувствительностью понимают отношение относительного изменения функции &Н(р)/Н(р} к относительному изменению параметра Дх/х:
 | |||||||
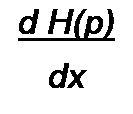 | |||||||
 | |||||||
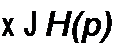 | |||||||
Применительно к установившемуся синусоидальному режиму рассматривают чувствительность модуля и чувствительность аргумента //(/ со.)
Для резонансных систем с высокой добротностью пользуются понятием корневой чувствительности, имея в виду чувствительность Н{р) к изменению положения нуля или полюса этой функции, находящегося вблизи мнимой оси плоскости комплексной частоты.
Понятие чувствительности используют главным образом в задачах синтеза. Электрические цепи стремятся сформировать так, чтобы они
были по возможности малочувствительны к изменению параметра. Если Н(р) зависит от многих параметров и все они могут изменяться, то верхней границей возможной ошибки считают сумму модулей чувствитель- ностей по всем параметрам. При определении классической чувствительности можно воспользоваться теоремой вариаций (см. § 2.19) и теоремой Теллегена (см. § 3.43).
§ 8.66 Обобщенные функции и их применение к расчету переходных процессов. Обобщенными функциями (ОФ) называют функции времени fit), которые терпят разрыв, например при г = 0. Значение функции при t <0 обозначим А (О, при />0 А (О (рис. 8.50, в).
Имея в виду фильтрующее свойство единичных функций, можно записать
f W = f- (О К-0 + Ш ко.
В общем случае /(/) может содержать также 8-функцию и ее производные, Производная от /(/)
А/ м/ ч r'/м/ч г / ч
= А (О к-0 + А (О КО + А (О А (0 ~~ =
dt d(-t) dt dt
= а'(О к-0 + л’ (О КО + 5(r) (A (0) - A (0)L
Используя ОФ, можно решать задачи на переходные процессы, о которых говорилось в § 8.28, а также задачи на импульсные воздействия. В этом случае необходимо составить уравнения для послекоммутацион- ной схемы, выразить токи, напряжения и их производные через ОФ и, воспользовавшись фильтрующим свойством l(-r), l(z), и 8(/), приравнять в этих уравнениях коэффициенты, содержащие только !(-/)> только !(/) и только 8(/), затем решить их совместно.
Пример 107. Путем использования обобщенных функций решить задачу примера 86 (см. рис. 8.26).
Решение. В уравнении для послекоммутационной схемы подставим
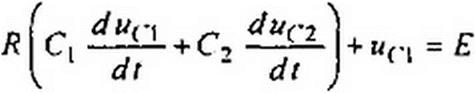 | |||
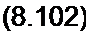 | |||
“л = *л-(О Ц“0 + «л+0) 1(0;
и ('2 = ис2-{{У U-0 + исг*(О КО;
u ci - К_О + т,{I) КО + 5(О (0,) - U(~।(0_)];
«С2 - «С2(О Ц-0 + «гзЛО1(0 + S(O 1«С2(°+) - «С2(°-)]•
£ = £!(-/) + £![/].
Коэффициенты яри 1(~г), 1(0, и 6(/) дают три уравнения:
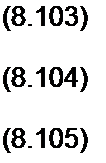 Л (С| W^)+(0 + Cj «Г2-(0)+ Uci-V) =
Л (С| W^)+(0 + Cj «Г2-(0)+ Uci-V) =
Я(С( »cu(0 + C2 Uc2+(0) + «Cb(/)= Е>
u Ci (0* ) (Q + С'2);=С1 uCl(Q-) + С-2 и('2^-У
Из (8.103) u(?1_ (/) = £, из (8.105) Wc)(0*) = C] £/(C)+C2); далее решаем (8.104) классическим или операторным методом, имея в виду, что (/) = иГ2 </). В результате получаем тот же ответ, что и в примере 86.
§ 8.67 Интеграл Дюамеля для огибающей. Положим, что на вход четырехполюсника, имеющего переходную функцию Л(г), воздействует синусоидальное напряжение единичной амплитуды
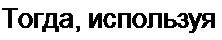 иДО = I sin о i - lme7<D/.
иДО = I sin о i - lme7<D/.
рмулу интеграла Дюамеля, определим напряжение на выходе четырехполюсника:
и2 (0 = 1т((Л(0) + j*’(T) е‘,<3 ' dx) е'w/) = 1т(а(ш,г) е'“'). (8.106)
Здесь о
<
о(<о,0 - Л(0)+ J/f(r) е"7"1 dx = /«(©,/) + j л(о.О = . (8.107)
о
где а(ы, /) —огибающая выходного напряжения при воздействии синусоидального и((/). Воздействуем на вход четырехполюсника амплитудно-модулированным синусоидальным напряжением
1/|(г)=1л1((/я1(г)е/т')
и определим
и2(/) = 1гп((/?(0) (/„,(/) + р’(т)U„,(t) (/ - т)e-/tt ’ dx)е'"').
О
Учтем, что —*-■ -Л'(т)е'1шг ~а'(и).т) и Л(0) = о(е,0). Тогда
dt
«>(/) = 1т(Л(и.г) eywZ). (8.108)
где
>4(aj) = a(0,O)t/w(r)+ |о'(<о,т) Um(J~ *)dx\ (8.109)
о
/l(w,z) — огибающая выходного напряжения. Формулу (8.105) называют интегралом Дюамеля для огибающей, она позволяет, не вдаваясь в мелкие детали, выявить макроструктуру переходного процесса.
Пример 108. Определим огибающую тока в цепи, когда на вход последовательно соединенных R и L воздействует напряжение и,(/) = к t sin <о t.
1
Вместо h(t) используем g(t) = — (l-e ). R
В соответствии с формулой (8.107)
о(<й,г) = 5(0)+ fg'(x) е-?от dx~-—!---------------------------------------------------------------- (1-е-*');---------------------------------------------------------------- = —+ >ш.
J R + j L L
Учтем, что g(0) = 0, = -J-e ч\ Um (t-т) = к (/ - т).
Огибающая тока в пели по формуле (8.109):
.. . к t. . -q х j к? к Lt —at к I*
= — (г - т) с * dx - ----------- --------- - +-------------------- (е ? -1) = —-------------------------------
L ' R + jaL (/? + ;<о£)2 Л2+(соО
I, ~ *' ч2 z К>
Il R t **------------- I J----------------------- —
У — + е 1- cos(<o t + 2 <p) - cos 2 <p + |wz + e L sin(co t + 2 (p) - sin 2 ф
x A J \
Rf
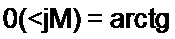
 tof + e L sin(w / + 2 ф) - sin 2 q>
tof + e L sin(w / + 2 ф) - sin 2 q>
Rt
R t -b~~
— + e f- cos(co t + 2 ф) - cos 2 ф
Вопросы для самопроверки
1. Дайте определение переходном}' процессу. 2. Что понимают под принужденными и свободными токами и напряжениями? 3. Сформулируйте законы (правила) коммутации. 4. Дайте определение зависимым и независимым начальным условиям. 5. Какие вы знаете способы составления характеристического уравнения? 6. Объясните, почему при составлении характеристического уравнения путем приравнивания к нулю входного сопротивления Z(p) = ЛЧр)/Л/(Г) в общем случае нельзя сокращать числитель и знаменатель дроби на общий множитель. 7. Чем определяется число корней характеристического уравнения? 8. Изложите сущность классического метода расчета и принцип составления уравнений для определения постоянных интегрирования. 9. Переходный процесс в некоторой цепи сопровождается биениями. О чем это может свидетельствовать? 10. Дайте обоснование обобщенным законам коммутации. 11. Запишите известные вам соотношения между /(О и Г(р), а также теоремы операторного метода и предельные соотношения. 12. Почему/? называют комплексной частотой? 13. Охарактеризуйте этапы расчета операторным методом. 14. В чем особенности расчета переходных процессов операторным методом при синусоидальном источнике и ненулевых начальных условиях? 15. Охарактеризуйте свойства единичной функции !(/) и свойства дельта-функции 5(f). 16. Определите переходную и импульсную переходную проводимости (сопротивления). Укажите, с какой целью они используются. 17. Охарактеризуйте идею расчета с помощью интеграла Дюамеля. 18. Прокомментируйте известные вам формы записи интеграла Дюамеля. 19. Какими спо-
 | |||
 | |||
| ||||
| ||||
 |
| ||||
| ||||
собами можно определить отзвук системы, когда на нее воздействует импульс напряжения или тока? 20. Поясните принцип работы интегрирующих и дифференцирующих цепей. Запишите условия, при которых эти цепи выполняют свои функции. 21. Чем следует руководствоваться при формировании дополняющих двухполюсников? 22. Поясните идею расчета переходных процессов с помощью обобщенных функций. 23. Перечислите основные этапы расчета методом переменных состояния. 24. Как составляют уравнения переменных состояния путем сведения послекоммутационной схемы к чисто резистивной?
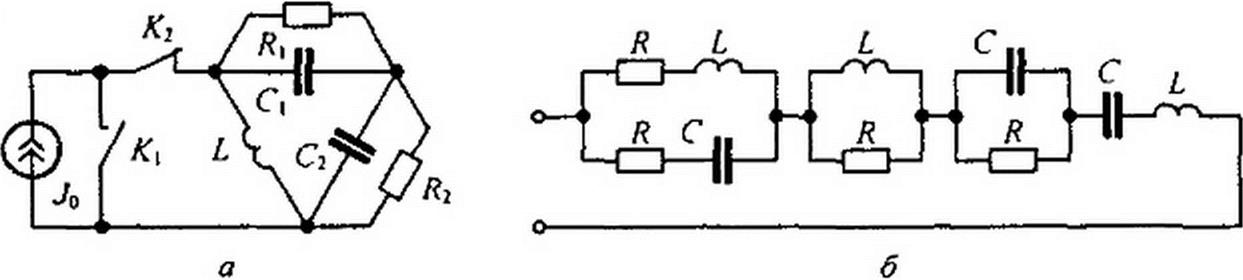
25. Охарактеризуйте сильные и относительно слабые стороны известных вам методов расчета переходных процессов. 26. Что понимают под системными функциями? Какие виды чувствительности системных функций вы знаете? 27. В схеме на рис. 8.51, а с источником тока Jq в момент / = 0 одновременно размыкается ключ Кг и замыкается Показать, что заряды, протекающие через сопротивление и Я2 за время от 0 до не
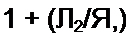 зависят от емкостей Q и С2. Определить величины этих зарядов. (Ответ:
зависят от емкостей Q и С2. Определить величины этих зарядов. (Ответ:
.) 28. В схеме рис. 8,6. а при размыкании ключа происходит переходный
процесс. Определить законы изменения во времени напряжений и( ) и «сг на конденсаторах. Задано j(t) = I sin(wt+ 90°) А, /? = 1/юС = 1Ом. со = 100рад/с. (Ответ: uCi = 0,447 sin(<o I + 63°27') -0,253 - 0.15 е-'200' В; «Г2 = О-447 $in«»' + Ы°2?') + 0,253 - -О,15е‘у200' В.) 29. Покажите, что в симметричной мостовой схеме (рис. 8.51, в), в
I
которой выполняется условие £,/<’=/?2, переходная функция Л(/)»-у+е 4 . 30. В схеме рис. 8.51, б R = L - С = 1. Покажите, что входная переходная проводимость равна t е"'.
31. Покажите, что энергия, запасаемая в L схемы рис. 8.51, е (начальные условия нулевые), равна тепловым потерям в R. 32. Первичная обмотка трансформатора рис. 8.51,0 при нулевых начальных условиях подключается к источнику постоянной ЭДС Е, R} - R2 = R: L}=L2=M. Определите q(0^), /2(0„). (Ответ: /((0+) = -/2(0+) = £/ (2 R).) 33. Определите степень характеристического уравнения для схемы рис. 8.52. (Ответ: пятая.)
34. Как определить К(р) через h(t) и через Л&(/)?35. По h(r) = — (1 + 2е [6]- ) четы
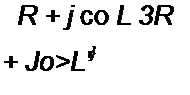 | |||||||||||||
 | |||||||||||||
 | 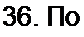 | ||||||||||||
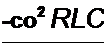 | |||||||||||||
 | |||||||||||||
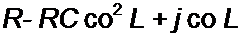 | |||||||||||||
/? = 0,2Ом. С = 5Ф, £ = 1Гн. (Ответ: Л(/) = 1,62е-0,724'-0.62 е’0,276/.) 37. На вход че-
J fc)
тырехполюсника с K(j со) =------------------ воздействует единичный импульс напряжения в виде
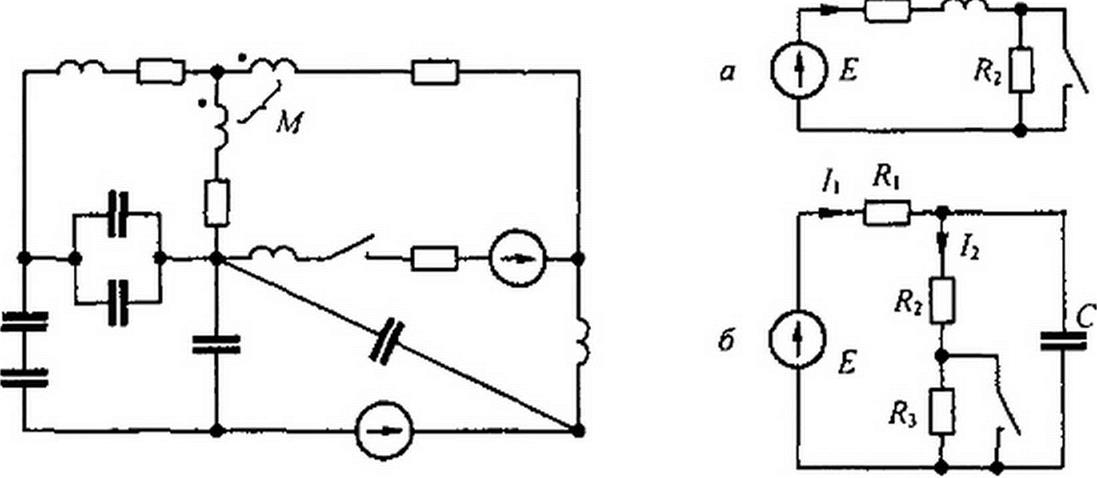
5-функции. Определите напряжение на выходе четырехполюсника после окончания действия импульса. (Ответ: 0,25 е"^5'.) 38. В схеме на рис. 8.53, а до коммутации был установившийся режим; £ = 20В, Jim р/](р) = 2А и lim р /((р) = 5 А. Определите Л, />->0
и R2. (Ответ: Я, = 4 Ом, Я2 = 6 Ом.) 39. В схеме на рис. 8.53, б до коммутации был установившийся режим; £ = 10 В, limp/2(p) = 2A и Нт р 12(р) = 1,428 А. Определите />-»» р~»О
Я, и Я3, еслиЯ3 = Я2. (Ответ: Я, =4 Ом, Я2 = 3 Ом.) 40. Решите задачи 11.4; 11.12; 11.15; 11.26; 11.29; 11.32; 11.38; 11.40; 11.47; 11.50; 11.55; 11.57.
| Глава девятая ИНТЕГРАЛ ФУРЬЕ. СПЕКТРАЛЬНЫЙ МЕТОД. СИГНАЛЫ |
| § 9.1. Ряд Фурье в комплексной форме записи. Как известно из предыдущего (см. § 7.2), в ряд Фурье можно разложить любую периодическую функцию /(/), удовлетворяющую условиям Дирихле. Обозначим период функции Г, а основную частоту — соо = 2 л !Т. Ряд Фурье можно записать двояко. Первая форма записи: |
| 00 Л0=4 + Х4 sin<* |
| вторая форма записи: |
| /(/) - Ло + (Л£ sin к o)0 t + Ак cos к со0 /), *=| |
| (9-D (9-2) |
| где — постоянная составляющая ряда; Ак — амплитуда ^-гармоники ряда; — начальная фаза А-гармоники; |
| А'к - Ак cos ук; Ак - Ак sin ; |
| i 772 4) = 7 f ЛО 1 -тн |
| Т!2 ]/(/) sin к w0 t dt\ -TH |
| (9-3) (9-4) |
| 772 ]"/(/) COS А (00 1 <*1- -TH |
| (9-5) |
| ~&~JX Из курса математики известно, что sin х =------------------- . Следовательно, 2 У |
| e J(k ®0+ч/4) _e-(*®o+Vi) sin(A соо t + у J -------------------------------------- —--------------- 2у |
| (9.6) |
| Подставив правую часть формулы (9.6) в выражение (9.1), получим |
| (9.7) |
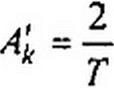
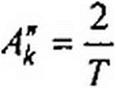
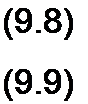 Обозначим
Обозначим
А.к =-лк e,4t.
Тогда ряд (9.7) можно записать так:
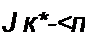 (9-10)
(9-10)
Формула (9.10) представляет собой комплексную форму записи ряда Фурье. Текущий индекс к может принимать все целые числовые значения от -со до +<», но не может равняться нулю, так как постоянная составляющая ряда выделена в виде отдельного слагаемого.
Пример 109. Представить функцию f(t) = 2 + 3 sin(o0 t + 30°) + 2 sin(2 co0 /- 45°) в комплексной форме записи.
Решение. Ло=2; Д =3eyJ0’; 4, = -Зе*'34 Л2 = 2 е’ 42=-2еу45‘;
у (у) _ 2 4. 1 (3 1 + _ 3 g”? (иу “ +30*) 2 f-45*) _ 2 /-45”)
2 У
Составим выражение для комплексной амплитуды Ак. По определению (см. формулу (9.8)),
4 = 4 e>Vx = Ак C0SVa + J 4 sin = 4 + j Л”к, (9.11)
где 4 определяется формулой (9.4), 4 — формулой (9.5).
Подставим правые части формул (9.4) и (9.5) в формулу (9.11):
2 772
4=~ J7(0 (sin к ©о t + j cos к ©0 /) d{ = ' -77 2
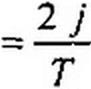 772
772
Jf (t) (cos к o)0 t - J sin к ©0 t) dt,
-7/2
или
Ak dl. (9.12)
' -772
Подставим правую часть формулы (9.12) в формулу (9.10):
7/2
7(') = Л+ Z ^*“"'1 dt. (9.13)
к » -ОО / -7’/2
§ 9.2. Спектр функции и интеграл Фурье. Ряд Фурье — это тригонометрический ряд, представляющий собой изображение периодической функции суммой синусоид, амплитуды которых конечны, а аргументы кратны основной частоте ©0.
Под интегралом Фурье понимают тригонометрический ряд, представляющий непериодическую функцию суммой бесконечно большого числа синусоид, амплитуды которых бесконечно малы, а аргументы соседних синусоид отличаются на бесконечно малые значения.
Формулу для интеграла Фурье получают из формулы для ряда Фурье (из формулы (9.13)) предельным переходом при стремлении периода Т к бесконечности.
На функцию /(/) при представлении ее интегралом Фурье наклады- -нх>
вают ограничение, а именно, полагают, что $f(f)dt есть величина
конечная (не бесконечно большая). Это серьезное ограничение. Ряд функций этому условию не удовлетворяет'’. । т/2
Так как по определению (см. формулу (9.3)), Л = ~ f/(0 а при +со -7/2
Т —> оо [/(f) dt есть величина конечная, то Ао = 0.
] 7/2
Преобразуем выражение — j/(f) е"/А ' с/f, стоящее под знаком -772
суммы в формуле (9.13). С этой целью произведение к <оо заменим на со (под со будем понимать изменяющуюся (текущую) частоту). В ряде Фурье разность двух смежных частот Дсо=©о =2 л/Т. Следовательно, МТ = До)/(2 л).
При Т -> оо, заменив Део дифференциалом с/со, получим
1 '(/О)Л = Л.
1 -Т/2 71 -77 2
 Обозначим
Обозначим
5(/о) =
-со
Формула (9.14) дает возможность преобразовать функцию времени /(f) в функцию частоты S(J со); преобразование (9.14) называют прямым преобразованием Фурье, a S(j о) — спектром функции f(t). Это комплексная величина, зависящая от вида функции /(f). В соответствии
772 j
 f/(f) dt на — S(y to) d® и учтем, что
f/(f) dt на — S(y to) d® и учтем, что
•Лл 2 л
*’ Средн функций /(/}, для которых интеграл ^f(t)di расходится, наиболее важной для практики является функция /(/) = А, где А — постоянное число. Для того чтобы эту функцию представить интегралом Фурье, пользуются следующим приемом. Находят интеграл Фурье для функции /(/) = Ле’₽/. где р>0 и /(/) = 0 при t<Q. Для этой функции J/(z) dt сходится, поэтому она может быть представлена интегралом Фурье.
Далее в полученном выражении устремляют р к нулю.
при изменении к от -оо до +<ю со = к со0 также изменяется от -оо до -ню. Следовательно,
i (0- 4-00
ЛО = у- X S(jo)е‘J‘' А».
(О ш -ОС
Заменив сумму интегралом, найдем
1 -rw
 Л0 = — Js(> а>) rfw.
Л0 = — Js(> а>) rfw.
Формула (9.15) представляет собой запись интеграла Фурье (формулу обратного преобразования Фурье). Она выражает непериодическую функцию f(t) в виде бесконечно большого числа синусоидальных колебаний с бесконечно близкими частотами и бесконечно малыми амплитудами S(j(&)d(j3 (S(j со) конечно, но произведение S(j d® бесконечно мало, так как бесконечно мало значение с/со).
В соответствии с формулой (9.15) для нахождения реакции системы на любое воздействие следует его представить в виде бесконечно большого числа гармонических воздействий, символическим методом найти реакцию системы на каждое из воздействий и затем просуммировать реакцию на все воздействия.
Преобразования (9.14) и (9.15) являются взаимно обратными.
Отметим, что представление функции f(t) в комплексной форме в виде интеграла Фурье (формулы (9.15)) привело к необходимости формально ввести отрицательную угловую частоту. При этом сумма слагаемых подынтегральной функции (9.15) при ±со дает синусоидальные колебания частоты со.
Сопоставим формулу (9.14) с формулой преобразования по Лапласу:
со
F(p) = f/(r) е'" Л, (9.16)
о
когда /(г) = 0 при t <0.
Если учесть, что f(t) = O при /<0, и заменить р на у со, то (9.16) переходит в (9.14). Следовательно, формулы для спектра функции SV о) могут быть получены из соответствующих выражений для изображений по Лапласу, если в последнихр заменить на у со.
Пользуясь соотношениями § 8.39, найдем спектр функции f(t) = е~а/, полагая, что /(/) = 0 при t <0.
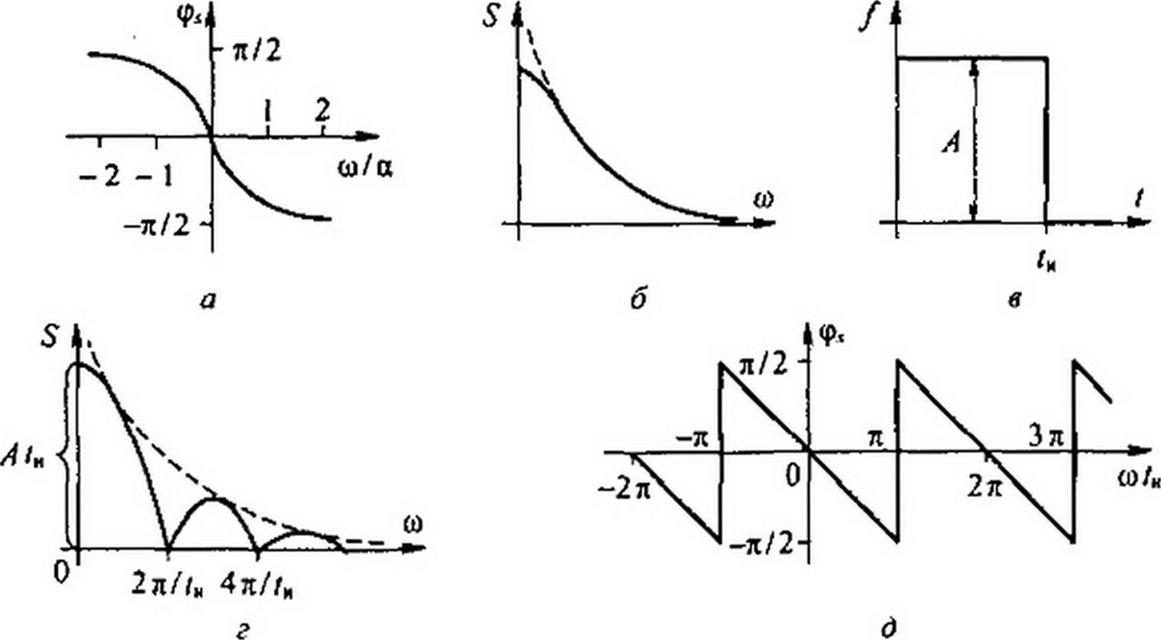
Изображение ее по Лапласу 1 / (а + р). Заменим р на j со и получим спектр S(j со) = I /(а + j со); S(j со) есть комплексная величина, равная S(co)ey<₽‘. Модуль ее равен 1/Vet2 ч- со2 , аргумент фл. = arctg(-co/a). Графики для экспоненциального импульса изображены на рис. 9.1, а, б.
Пример 110. Найти S(o) и ф<со) для прямоугольного импульса (рис. 9.1, в) амплитудой Л и длительностью
 |
|
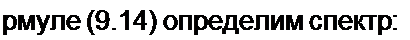 | ||||||||||||||
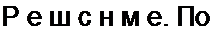 | ||||||||||||||
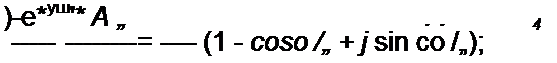 | ||||||||||||||
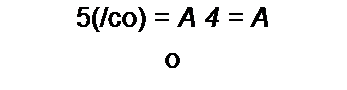 | ||||||||||||||
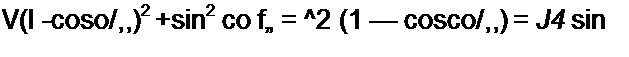 |  | |||||||||||||
 | ||||||||||||||
 | ||||||||||||||
S(co) = —sin = A /
co /„ 2
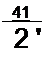 График этой функции приведен на рис. 9.1.?. Штриховой линией показана огибающая. Аргумент ф¥ для прямоугольного импульса вычислим по формуле
График этой функции приведен на рис. 9.1.?. Штриховой линией показана огибающая. Аргумент ф¥ для прямоугольного импульса вычислим по формуле
cos со -1 со /..
tg Ф., = —:—-— = - tg-r21- sin со /„ 2
График Ф, дан на рис. 9.1, д. При значениях со/,, = л. Зя.... фл возрастает скачком на л.
Обратим внимание на то, что при определении S(J со) путем замены р на j со в формуле для F'(p') следует соблюдать некоторую осторожность, если функция /(/) имеет импульсный характер, иначе можно потерять импульсную компоненту в S(J со) в виде дельта-функции. Например, изображение функции 1(0 по Лапласу равно \/ р, тогда как
I
спектр £(/со) функции 1(f) равен не l/yco, а л5(со) +------------------------------------------------------------- . Чтобы
j®
показать это, определим спектр функции 1(/) е”р' (Р > 0), а затем устремим р->0:
е-и/ е-у«>/ dt 1-------------- р у m
P + J<0 Р~ +(0“ Р2+СО2
Первое слагаемое правой части при 0 -> 0 и при со -> 0 стремится к бесконечности, т. е. имеет вид дельта-функции а 8(со), второе слагаемое правой части при (3—>0 равно 1//<о. Чтобы вычислить коэффициент а, проинтегрируем р/(02 + со2) = а 5(со) по со от -оо до +а>:
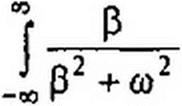 |
|
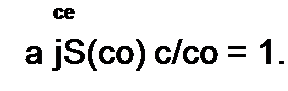 | |||||||||||||||||||
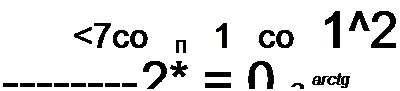 | |||||||||||||||||||
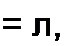 | |||||||||||||||||||
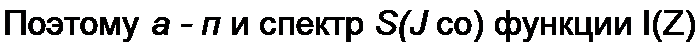 | |||||||||||||||||||
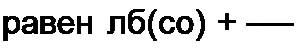 | |||||||||||||||||||
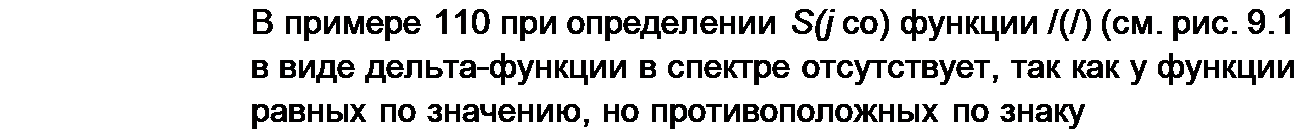 | |||||||||||||||||||
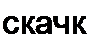 | |||||||||||||||||||
 | |||||||||||||||||||
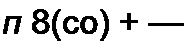 | 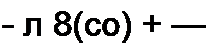 | ||||||||||||||||||
л5(со) выпадают.
§ 9.3 Спектр функции, смешенной во времени. Спектр суммы
 функций времени. Если функции времени /(/) соответствует спектр
функций времени. Если функции времени /(/) соответствует спектр
9(7 со), то функции соответствует спектр е”уыт S(j со), что следует из теоремы смещения в области оригиналов (см. § 8.40), если заменить р на j со.
Так как модуль функции е"ушт равен единице, то модуль спектра функции /0-т) равен модулю спектра функции /(/), т. е. равен 5(<о), однако аргумент спектра функции f{t - т) отличается от аргумента спектра функции /(г) на -сот.
Если /(/) представляет собой сумму нескольких функций времени, например /(/) = /(/) + /2(0» а каждая из них имеет спектр соответственно (у со) и S2(j то спектр S(J со) функции /(г) равен сумме спектров этих функций, т. е. S(J со) - S}(j со) + S2(y со). Это следует из линейности преобразования (9.14). Однако модуль S(co) * ^(со) + 52((о) и аргумент срА.(со) * срд| (со) + <рд2(со).
§ 9.4 Теорема Рейли. Теорему Рейли (Релея) записывают следующим образом:
(9.17)
Функция /(/) = 0 при г<0; S(co) представляет собой модуль спектра 5(7 со) функции /(/):
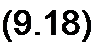 5(7 а) = J/We-'"' dt.
5(7 а) = J/We-'"' dt.
-СО
Если принять, что f(f) есть напряжение, приложенное к активному сопротивлению 1 Ом, то левая часть в (9.17) представляет собой энергию, выделяющуюся в этом сопротивлении.
Таким образом, площадь квадрата модуля спектра 5(со), разделенная на я, является энергией, рассеиваемой в активном сопротивлении, на которое воздействует /(/).
Основой при выводе теоремы Рейли служит обратное преобразование Фурье:
4
7(0 = — р(/о>) е'“'Ло.
2 It *
-со
Умножим обе части последнего равенства на /(/) и проинтегрируем по t от -со до 4-ос:
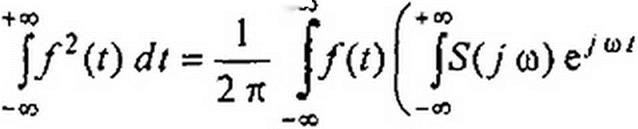 |
| ||||
| ||||
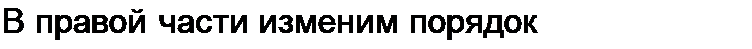 | |||||||
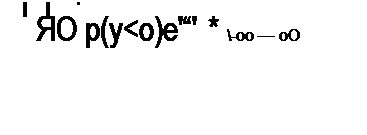 | |||||||
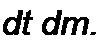 | |||||||
 | |||||||
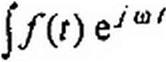 |
|
-со
следовательно,
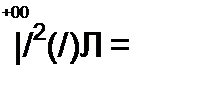 +со | +О0
+со | +О0
\S(J со) S(-j w) dсо - — [S2 (со) dm.
J 2 л <
-00 -00
Для перехода к формуле (9.17) учтем, что при / < 0 функция /(/) = 0. Это дает возможность заменить в левой части нижний предел с -оо на 0. Приняв во внимание, что квадрат модуля 3’2(со) есть четная функция +00 +00
частоты, заменим J в правой части последнего уравнения на 2 В
-сс О
результате получим формулу (9.17). Величину 52(<о) называют спектральной плотностью энергии сигнала, а функцию S2(co):= /(со)—энергетическим спектрам.
§ 9.5. Применение спектрального метода. Спектральный (частотный) метод исследования процессов в электрических цепях основан на использовании понятий спектров воздействующих импульсов и частотных свойств цепей. Особенно широко его применяют в радиотехнике при
рассмотрении вопросов прохождения модулированных колебаний через усилители, фильтры и другие устройства, в импульсной технике при рассмотрении вопросов прохождения через четырехполюсники коротких импульсов длительностью порядка нескольких микросекунд, а в некоторых случаях даже нескольких наносекунд. Допускается, что модулированное колебание или, соответственно, импульс, пройдя через четырехполюсник, изменился по амплитуде, на некоторое время /0 запоздал во времени, но недопустимо, чтобы существенно изменилась форма им пуль са (колебания) на выходе по сравнению с формой импульса (колебания) на выходе. Недопустимость изменения формы импульса (колебания) следует из того, что именно в форме импульса (колебания) заключена информация, которую он несет.
Положим, что на вход некоторого четырехполюсника с передаточной функцией К(у со) - К"(со) е7Ф<<0) при нулевых начальных условиях воздействует сигнал /j(/), имеющий спектр 5вх(у со). На выходе четырехполюсника появится сигнал /2(/), спектР которого
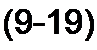 ^ВЫХ(jg)) = /C(;co)Sbx (у св),
^ВЫХ(jg)) = /C(;co)Sbx (у св),
4-00
где S,x0 <o)= (ЛОТd’-
-СО
Так как сигнал /2(/) может отличаться от сигнала по значению (по амплитуде), положим в а раз, и запаздывать на некоторое время /0, но по форме должен быть таким же, как и /(f), то можно записать, что /2<О = я/1('-'о)-
Если к функции /2(/) применить преобразование Фурье, то окажется, что спектр функции /2(г) равен
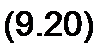 aS„xO<o)e^“'“.
aS„xO<o)e^“'“.
|
Сравнивая (9.19) и (9.20), замечаем, что
K(j со) = К(со) е7 Ф(С1>) = а е"7°'('.
Следовательно, для прохождения импульса или модулированного колебания через четырехполюсник без искажения формы необходимо, чтобы модуль передаточной функции был постоянен (не зависел от частоты), а аргумент <р(<в) = -со/о линейно изменялся в функции частоты (рис. 9.2, а).
В реальных четырехполюсниках эти условия могут быть выполнены лишь приближенно в некоторой полосе частот, которую называют полосой пропускания. Полоса пропускания ограничена значениями со, при которых отношение максимального значения
/С(со) к минимальному равно J1 (рис. 9.2, б). Такой характеристикой обладает, например, схема рис. 3.42, а. Для этой полосы приближенно полагают, что = const; <р(со) = -со /0.
Для того чтобы сигнал при прохождении через четырехполюсник не изменил своей формы, необходимо, чтобы важнейшие гармонические составляющие частотного спектра сигнала находились внутри полосы пропускания четырехполюсника. Для импульсных сигналов треугольной, трапецеидальной, прямоугольной, колоколообразной и некоторых других форм принимают, что они занимают полосу частот от со = 0 до со = 2 л//и, где — длительность импульса.
Если же необходимо передать через четырехполюсник основную часть энергии сигнала (например, 90 % энергии сигнала), то полосу частот можно сузить примерно до 0-г1//и.
Так как в полосе пропускания идеальные условия для прохождения импульса все же не выполняются, то, проходя через четырехполюсник, импульс в какой-то степени искажается. Определить степень искажения можно двумя способами, основанными на частотных представлениях.
Первый способ состоит в непосредственном применении прямого и обратного преобразований Фурье.
Основные этапы этого способа таковы:
1) нахождение спектра Ц(усо) входного сигнала w,(/);
2) определение передаточной функции четырехполюсника K(j со);
3) получение спектра выходного сигнала U2(j со) = K(j со) Ц(/ со);
4) вычисление w2(r) по (ЛД/со).
Последнюю операцию можно осуществить с помощью формулы (9.15), но практически ее удобнее выполнить, используя таблицу изображения по Лапласу, заменив на р в U2(ja)).
Такое решение мало чем отличается от решения той же задачи операторным методом и для сложных схем оказывается малопригодным, поскольку решение излишне громоздко, и, пользуясь им, трудно сделать вывод о том, как тот или иной конкретный элемент схемы при неизменных остальных влияет на фронт и на вершину импульса. Пользуясь этим методом, трудно также судить о том, какие элементы схемы в наибольшей степени влияют на деформацию фронта, какие — на деформацию вершины импульса.
В литературе по импульсной технике получил распространение второй способ решения, также основанный на спектральных представлениях. В основу его положено то обстоятельство, что искажение формы фронта выходного импульса по сравнению с формой фронта входного импульса зависит от свойств передаточной функции четырехполюсника на высоких (теоретически на бесконечно больших) частотах, а искажение вершины импульса определяется свойствами передаточной функции на низких частотах (теоретически на частотах, близких к нулю). Эти положения соответствуют предельным теоремам операторного метода (см. § 8.40).
Для того чтобы выяснить влияние отдельных элементов схемы на искажение формы импульса, прежде всего составляют полную схему замещения четырехполюсника, учитывая в ней все факторы, влияющие на частотные свойства (паразитные емкости ламп, импульсных трансформаторов, индуктивности рассеяния трансформаторов, емкостные свойства р—«-переходов транзисторов, зависимость коэффициентов усиления транзисторов от скорости процесса (от частоты <л)).
Затем из полной схемы замещения образуют две расчетные схемы. Первая схема представляет собой расчетную схему для высоких частот и позволяет определить степень искажения фронта импульса. Эту схему получают из полной схемы замещения путем закорачивания последовательно включенных конденсаторов по пути следования сигнала (относительно больших по сравнению с паразитными) и разрыва индуктивных элементов, включенных параллельно резистивным элементам схемы.
Вторая схема представляет собой расчетную схемы для низких частот и служит для выяснения степени деформирования вершины импульса. Эту схему получают из полной схемы замещения, оставляя в ней последовательно включенные конденсаторы по пути следования сигнала, а также индуктивные элементы, включенные параллельно резистивным сопротивлениям, и закорачивая последовательные индуктивные элементы по пути следования сигнала. Паразитные емкости в низкочастотной схеме не учитывают.
В каждой из этих расчетных схем с учетом упрощений, рассмотренных в § 8.16, число оставшихся индуктивных элементов и конденсаторов оказывается значительно меньше, чем в полной схеме замещения.
Для каждой из схем характеристическое уравнение оказывается часто первой или второй, редко третьей степени, и поэтому влияние каждого из элементов схемы на искажение фронта и вершины импульса может быть выявлено относительно легко. Расчет переходного процесса в высокочастотной и низкочастотной схемах проводят обычно операторным методом.
Окончательный результат (кривую всего переходного процесса) получают, сопрягая решения этих двух схем. Вопрос об искажении заднего фронта импульса принципиально решается так же, как и вопрос об искажении переднего фронта импульса.
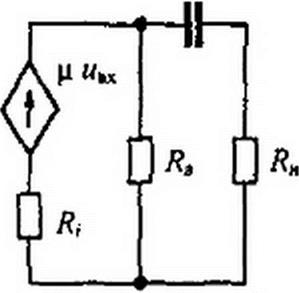
Проиллюстрируем сказанное примером. На рис. 9.3, а изображена схема лампового усилителя, где RH — нагрузочное сопротивление; Ср — относительно большая разделительная емкость (через нее проходит только переменная составляющая выходной величины); С2 —относительно малая емкость нагрузки и (или) емкость второго каскада усиления. Штриховой линией показаны источник анодного напряжения £н и малые по сравнению с Ср (по нескольку пикофарад) межэлектродные емкости анод—сетка Са^с, сетка—катод Сс_к и С| (емкость анод—-катод и емкость монтажа). В дальнейшем емкости Сс_а и Сс_к не учитываем, как оказывающие малое влияние на работу схемы.
Схема замещения для расчета переходного процесса при воздействии относительно малых по амплитуде переменных составляющих представлена на рис. 9.3, б. Она является схемой третьего порядка. Укороченные схемы для формирования фронта (рис. 9.3, в) и вершины импульса (рис. 9.3, г) являются схемами первого порядка.
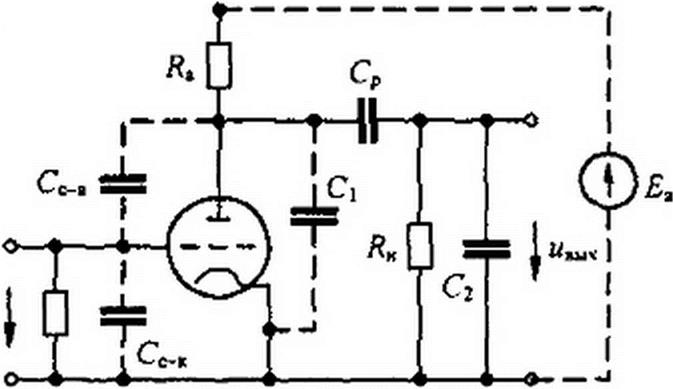 | ||||||
 | ||||||
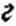 | ||||||
 | ||||||
|
 | |||||
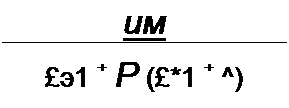 | |||||
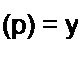 | |||||
РЛС £,] ---------- +------- +------- .
*/ *к
• <1 п
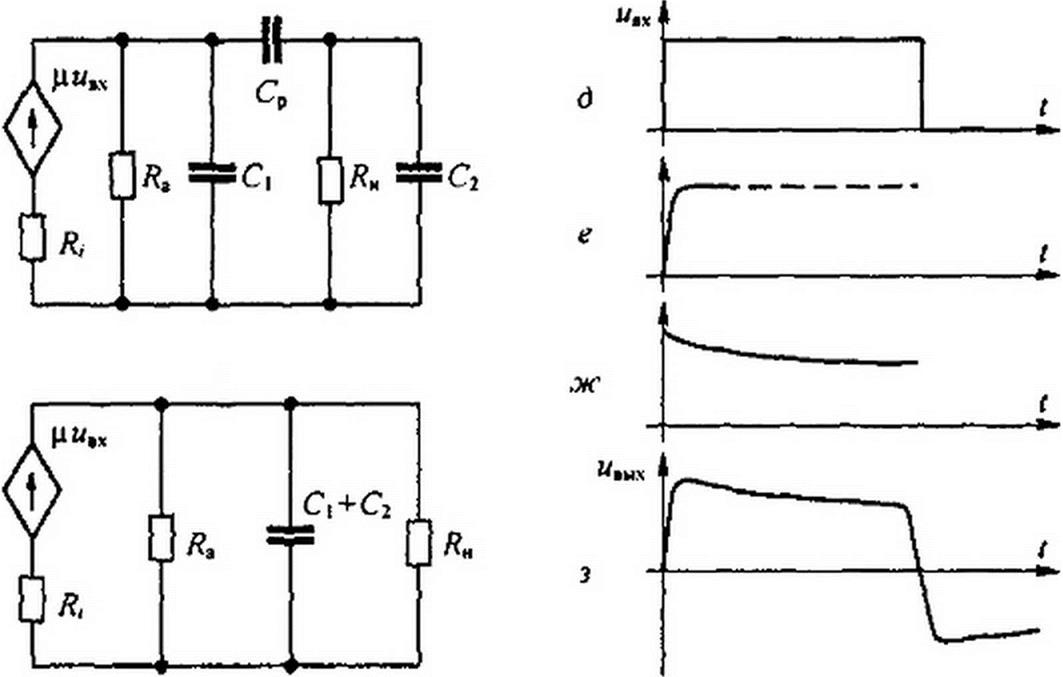
Для схемы рис. 9.3, г
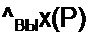
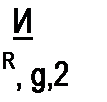
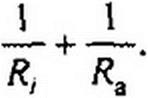
|
р С, ию (р)
рС
<?э2
Если входное напряжение представляет собой прямоугольный импульс рис. 9.3, д, то фронт выходного напряжения будет в виде нарастающей экспоненты рис. 9.3, е, а вершина — в виде спадающей экспоненты рис. 9.3, ж. Результирующая кривая нвых изображена на рис. 9.3, з. Подбор параметров усилителя осуществляют, исходя из допустимой деформации фронта и вершины выходного импульса по сравнению с входным импульсом.








