£ £ /?■> р, £ pt

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

4 = —--------- +----------- =— ; ь = — е' ;

(Z?) + £2) R] £(

и_с = £------- -— (l-e^z ); р =----------------------- ^!

R^ + R₂ Ri R₂ С

Полагая в этих формулах £ = 1 В. найдем:

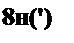— ¹ । _е Л,Л₂('.

+ /?2 (^| + ^2)

h ₍₁) = —ц __еР'у.
^ие Л, + Л₂

Подстановка числовых значений дает:

g_}, (/) = 0,00033 + 0,00067 е'³⁰' См; g₂₂ (t) = 0,001 е’³⁰' См;

=4O“^e~^3Of)-

Пример 99. Определить взаимную переходную проводимость между первой и третьей ветвями схемы на рис. 8.5 при включении источника ЭДС в первую ветвь и следующих значениях параметров: /?] =/?₂ = 100 Ом; 4^1 Гн; С = 100 мкФ.

Решение. Изображение тока третьей ветви

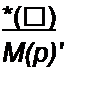______________ Е R₂ С
р² R₂ С + р (/?) /?2 "*■ "*• ^2

Корни уравнения Л/(р) = 0 (см. пример 76):

Р; =~100 + j100c“’; р₂ = -100-/ ЮОс^-1.

Полагая Е = 1 В, в соответствии с формулой разложения найдем

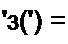После подстановки значений параметров, корней р, и р₂ и использования формулы (е^/х-е’^/х)/2 j = sinx получим

gjiU) = 0,01 е”'⁰⁰' sin 100/См.

Таким образом, взаимная переходная проводи­мость между третьей и первой ветвями схемы на рис. 8.5 при данных значениях параметров как функция времени представляет собой затухающую синусоиду.

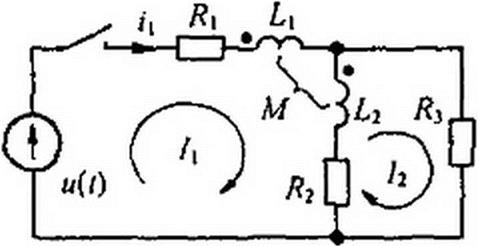
Пример 100. В схеме на рис. 8.38 w(/) = 170 sin(314 / + 30°) В; Л, = 10 Ом; Я₂ = 5 Ом; /?₃ = 15 0м; 2,!= 30 мГн; Л/=30 мГн; С = 50 мкФ. Найти /](/) с помощью формулы разложения.

Решение. Сначала устраним в схеме магнит­

ную связь между L_{ и £₂, затем составим уравнения по методу контурных токов:

+ R₂ + p{L_} + 4, + 2 <W))-/₂(/?)(/?₂ + p(L₂i-M))=W

— 1\{р) (Ri + P (^2 ^{+ +} (^2 ^3 P ^2^ ~ Q‘

Совместное их решение дает

_________ U„, (20 ч- 0,05 р)_________ ₌ Л'(р) (P-J w) (0.000875 р² + 2.6 р + 275) А/( р)'

Корни уравнения М(р) - 0:

Р;=314у, р₂ = -2860 и р₃ = -114с¹;

М’{р) = 0,000875 р² + 2,3 р + 215 + (р - J о) (0,00175 р + 2,6);

N(Pj) = 4301 е'⁶⁸°²⁰'; >У(р₂) = 123-17Ое'^2,о\ A'(p_s) = 14,29-170 е'³⁰*;

Л/'(Р]) = 838е^;77’; Л/'(р2) = ^{6930еУЬО16}; М'(ру) = 80бе^/110М0

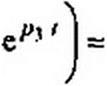
Ток

/(/) = 1m _е/т'
1лГ(р,)

= Im(5,13e><-^/-^s“⁴⁰> ₊3,03e-'²⁰³^' e'²⁸⁶⁰' ₊3,0l_e-^,,4') =

= 5.l3sin(w/-8°4O')-M6e'-⁸⁶⁰’ +1,97е'^ш' A.

§ 8.53 Интеграл Дюамеля. Познакомимся с третьим методом расчета переходных процессов в линейных электрических цепях — рас­четом с помощью интеграла Дюамеля.

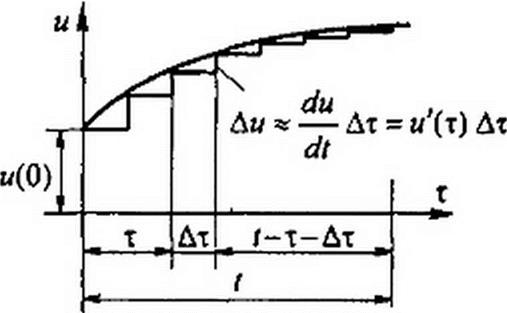
При использовании интеграла Дю­амеля переменную, по которой производится интегрирование, обозна­чим т а под t по-прежнему будем по­нимать тот момент времени, в который требуется найти ток в цепи. Пусть к цепи с нулевыми начальными услови­ями в момент времени f = 0 подключа­ется напряжение и(т) (рис. 8.39).

Для того чтобы найти ток в цепи в момент времени Г, заменим плавную кривую ступенчатой и просуммируем

токи от начального напряжения м(0) и

от всех ступенек напряжения, вступающих в действие с запозданием во времени.

Напряжение w(0) в момент времени / вызовет в цепи ток u(0)g(0), где g(0)— переходная проводимость. В момент времени т + Дт (см. рис. 8.39) возникает скачок напряжения

du

— Дт = и (т) Дт. dx

Для того чтобы найти составляющую тока в момент времени t, вызы­ваемую этим скачком напряжения Дм, необходимо м'(т)Дт умножить на значение переходной проводимости с учетом времени действия скачка до момента времени /. Из рис. 8.39 видно, что это время равно г-т-Дт. Следовательно, приращение тока от этого скачка составляет а'(т) g(i - х - Дт) Дт.

Полный ток в момент времени t получим, если просуммируем все частичные токи от отдельных скачков и прибавим их к току м(0) g(/): /(/) = м(0) g(t) + £м'(т) g(/ - т - Дт) Дт.

Число членов суммы равно числу ступенек напряжения. Очевидно, что ступенчатая кривая тем лучше заменяет плавную кривую, чем больше число ступенек. С этой целью заменим конечный интервал времени Дт на бесконечно малый dx и перейдем от суммы к интегралу:

z(/) - w(0) g(/) + Jw'(t) g(t -x)dx. (8.75)

о