Вычетом функции в некотором полюсе называют величину, на кото­рую уменьшается разделенный на 2 л j контурный интеграл от этой функции, когда контур при его стягивании пересечет этот полюс. Но

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

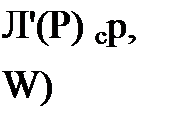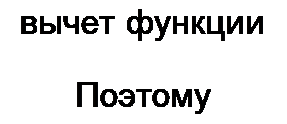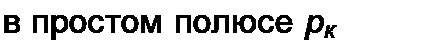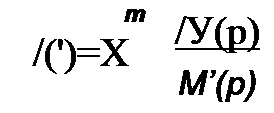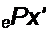Таким образом, используя обратное преобразование Лапласа, вывели формулу разложения (8.70).

2. Запишем формулу разложения при наличии кратных корней. Поло­жим, что уравнение М(р) = 0 имеет q простых корней (р\, р₂,---,Р_ч), корень р_г кратности г и корень p_s кратности s. Тогда

*(р) ,f _{Pil +} 1 Х21 е"

М(р)й«'(й) (r-iy.dp'-¹ М(р)

, I /У(р)(р-_А)-е'^>'

(5-1)! dp"' М(р)

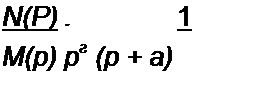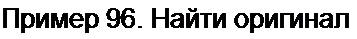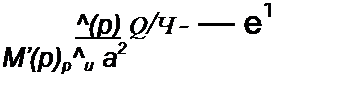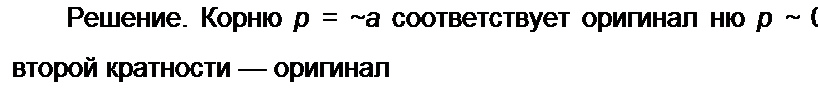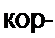d р² е^р> _ d e^/,f _ t с^р( (р + а}~с^р1 I

dp р^Г(р + а)Ц dp р + а (р + а)² Ц а а²

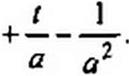1 е^-в/

Следовательно, —-------------- •=——

Р (р + а) а"

§ 8.51 Переходная проводимость. В § 2.15 указывалось, что ток i в любой ветви схемы может быть представлен в виде произведения напря­жения U на входе схемы на собственную или взаимную проводимость g: i = U g-

При переходных процессах это соотношение также имеет силу. Если на вход какой-либо цепи в момент ( = 0 включается постоянное напря­жение U (ЭДС Е), то ток /(/) в любой ветви этой схемы равен произведе­нию постоянного напряжения U на проводимость g(f):

<(0 = V gO). (8.73)

При переходном процессе проводимость является функцией времени, поэтому в скобках указывается время /; g(t) называют переходной про­водимостью. Она измеряется в тех же единицах (См), что и обычная проводимость.

Если в формуле (8.73) принять U -1 В, то /(/) = g(r), т. е. переходная проводимость какой-либо ветви схемы численно равна току /(О в этой ветви при подключении цепи к источнику постоянного напряжения в I В. Индексы у g(t) указывают на то, какую именно переходную проводимость имеют в виду. Если индексы одинаковы, то имеют в виду собственную переходную проводимость ветви, номер которой соответ­ствует цифре, указанной в индексе; если индексы разные, то — прово­димость между теми ветвями, номера которых указаны в индексе. Напри­мер, если источник постоянного напряжения U при нулевых начальных условиях включают в первую ветвь, то ток первой ветви /j(/) -U gn(/), а ток третьей ветви /₃(0 = U g_3l(/).

Переходную проводимость можно определить расчетным либо опыт­ным путем. При расчете g_w(/) классическим или операторным методом ток А-ветви находят при включении источника постоянного напряжения в /с-ветвь; g_km(t) ток Л-ветви вычисляют при включении источника по­стоянного напряжения U в m-ветвь. Далее, в полученных формулах по­лагают U - 1 В. При опытном определении переходной проводимости ток /(О соответствующей ветви находят путем осциллографирования.

В § 2.16 было доказано, что g^, = g„,*. Это свойство вытекает из симметрии опреде­лителя относительно главной диагонали.

Аналогично можно доказать, что операторное изображение проводимости £ъп(р) равно операторному изображению g_M*(p). Но если равны изображения двух переходных проводимостей, то равны и сами переходные проводимости, т. е. g*„,U) =

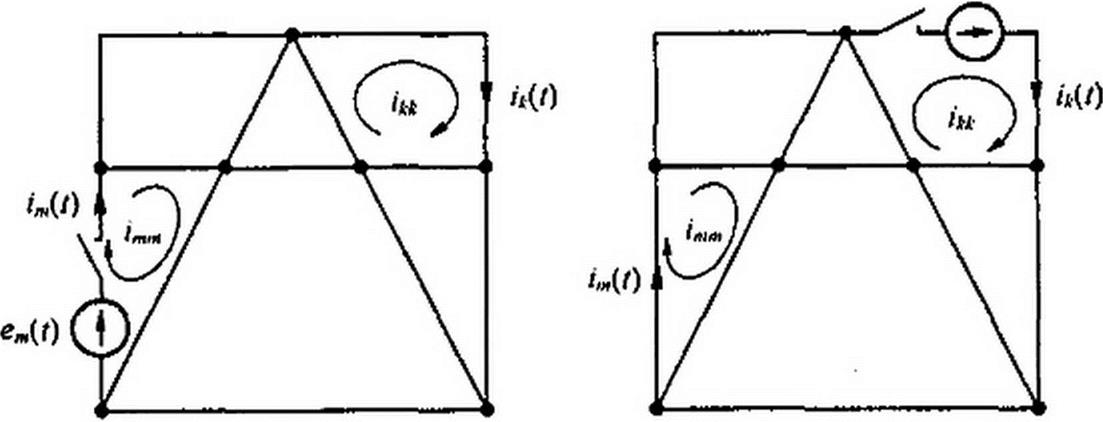
Данное равенство свидетельствует о том, что на переходные процессы распространя­ется теорема взаимности. Для переходных процессов теорема взаимности формулируется следующим образом (см. «скелетные» схемы рис. 8.36): в любой линейной электрической

еДО

а б

Рис. 8.36

цепи ток переходного процесса А-ветви 4(0, вызываемый включением источника ЭДС e_m(t) в ?я-ветвь (рис. 8.36, а), равен току переходного процесса 4,(0 в m-ветви, вызыва­емому включением источника ЭДС е*(/) в /г-ветвь (рис. 8.36, б), при условии, что е_к(1) = е_т(1).

§ 8.52. Понятие о переходной функции. При подключении линейной электрической цепи с нулевыми начальными условиями к источнику по­стоянного напряжения U между какими-то двумя точками а и b схемы возникает напряжение ы_а6(/), являющееся функцией времени и пропор­циональное воздействующему напряжению U:

u_oh(t) = Uh(l),

где h(t) — переходная функция. Это безразмерная величина, численно равная напряжению между точками а и Ь схемы, если на ее вход подать постоянное напряжение в 1 В; Л(Г), так же как и g(z), можно опреде­лить расчетным либо опытным путем.

Пример 97. Определить переходную проводимость схемы на рис. 8.2.

£

Решение. При замыкании ключа i(t) = — (I - е ¹- ).

По определению, переходная проводимость равна току в цели при £ = 1 В. Следова-

I

тельно, g(/) = —(1-е ¹- ).

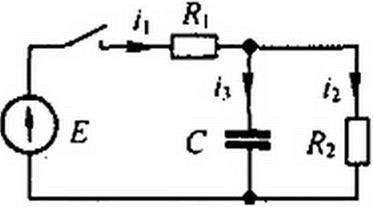
Пример 98. Найти собственную переходную проводимость первой ветви g_B(0, взаим­ную переходную проводимость между третьей и первой ветвями g?|(/) и переходную функцию напряжения на конденсаторе А„_г(/) для схемы на рис. 8.37. Параметры схемы: /?] =1000 Ом; /?₂ = 2000 Ом; С = 50 мкФ.

Р е ш е н и е. По определению,

С помощью классического метода определим: