2. Если начальные условия не нулевые, то в состав N(p) войдут внутренние ЭДС.
3. Если уравнение ЛУ(р) = 0 имеет комплексно-сопряженные корни, то слагаемые, соответствующие им в формуле (8.70), оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.
4. 
Если воздействующая на схему ЭДС синусоидальна: Ет sin(co t + vg) и изображение ЭД С взято в виде Ет да Ет = Еп, е7Ф, то при использовании формулы разложения из правой части ее для перехода от комплекса к мгновенному значению следует взять коэффициент при j (взять мнимую часть)*’. В соответствии с этим внутренние ЭДС, которые появляются в правой части формулы разложения при ненулевых начальных условиях в цепях с синусоидальной ЭДС, должны быть умножены на коэффициент у.
Умножить внутренние ЭДС на j необходимо потому, что только в этом случае наличие этих ЭДС будет учтено при взятии мнимой части от правой части формулы разложения. В цепях с постоянной ЭДС внутренние ЭДС умножать на j не нужно.
5. Если воздействующее на схему напряжение синусоидально, то принужденная составляющая решения входит в число слагаемых
' И 0ПРеделяется коРнем Р ~ 7 е0- Вычисление принужден
ной составляющей в виде члена этой суммы, соответствующего корню р = j <л, для сложных схем в большинстве случаев более громоздко, чем непосредственное вычисление ее с помощью символического метода. Поэтому для сложных схем переменного тока принужденную составляющую рекомендуется вычислять символическим методом.
’’ Мнимую, а не действительную часть из формулы разложения берут потому, что заданная ЭДС Е„, sin(en + у) есть мнимая часть комплекса Ет е7"' (см. гл. 3).
С помощью формулы, подобной формуле (8.70), можно определять не только токи и напряжения, но и многие другие функции времени: заряд конденсатора, скорость перемещения какого-либо тела механической системы и т. п.
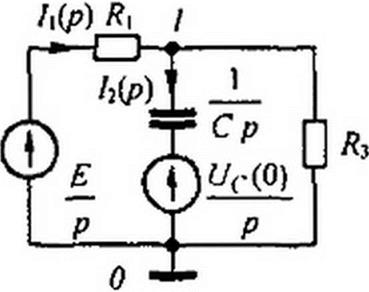
Пример 94. Определить ток уд/) в схеме на рис. 8.19 с помощью формулы разложения и сравнить с результатом решения классическим методом (см. пример 80), если £ = J50B: Л ==/?3 = 50Ом; С=Ю0мкФ; wr(0) = 50B.
|
Решение. Составим послекоммутаиионную операторную схему (рис. 8.35), имея в виду, что начальные условия ненулевые. Внутренняя ЭДС w<-(0)/Р позволяет учесть, что до коммутации конденсатор был заряжен до напряжения кг(0) током /2, поэтому она направлена встречно току /г(р). Узел 0 схемы заземлим. Потенциал узла / обозначим <р|(р) и определим его по методу узловых потенциалов:
ф)(р) = ^—^7—•
—+ С> + —
 | |||
 | |||
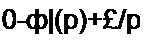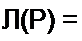По закону Ома для участка цепи с ЭДС,
После преобразований
(Е-ыг(0)> Р + £ = Л'(Р)
P(R] R3 Cp+Rf + Rj) М{р)
Уравнение W(p)=0 имеет корни
 | |||
 | |||
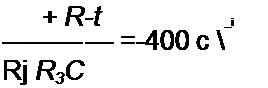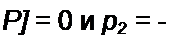поэтому
N(p|)=E = 150;
Л’(р2) = (150 - 50) ■ 50 • 100 (-400) • 10‘* +150 = -50;
M\p)~2Rl Rj С р+ R} + R3\
Л/’(Р[) = 100; ЛГ(р2) = -Ю0.
Ток в схеме на рис. 8.19
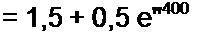
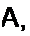150 (-50) е"400'
100 + (-100)
что совпадает с результатом примера 80.
Пример 95. Найти /(/) в схеме (см. рис. 8 21), применяя формулы разложения, и сравнить результат с результатом решения той же задачи классическим методом (см. пример 81).
Решение. Изображение синусоидальной ЭДС )27sin(314/-50°)
£(р) = Е, ——.
P-JU
где Em =127е'у50* В.
В схеме ненулевые начальные условия:
Цр) (Л22 + Р £) = Е(р) + »(0) /(0.) = -25,35 А.
Так как действующая в схеме ЭДС синусоидальна и изображение ее взято в виде > I
Ет------------ (£т — комплексная амплитуда), то в дальнейшем от правой части формулы
p-ju
разложения следует взять коэффициент при мнимой части (см. п. 4 § 8.49), поэтому умножим внутреннюю ЭДС L ДО) на J.
После небольших преобразований найдем
/(м- Em+jLWp-ja) = У(р)
(p-ju)(R2 + pL) М(р)
Следовательно,
N(p) - +J L '(°) (р - J а); М(р) = {p-j <о) (Я2 + Р Я.
Уравнение Л/(р) = 0 имеет корни pjsjcoc*1 и р2 =-Я2/£ =-210 с"*. поэтому
М\р} -R2 + pL(p~J со); М'(Р\) = 2 + 3 у = 3,61 е'56‘20';
Щрг^-З.би-'56*20' = 3,61 е_у123°40; Л*(^) = 127е ;soe;
М р2) = 127 е">50° + j (-210 - j 314) — (-25,35) = 5,4 - у 46,4 = 47,1 е"' 8Г“4'.
314
Ток
 | |||
 | |||
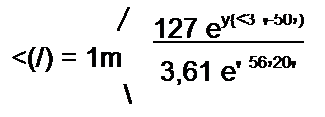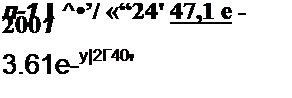= 35.2 sin(w t -106°20') +13.1 sin 40° 16' е-210' А;
13Д sin 40° 16' = 8.45.
Результат совпадает с результатом примера 81.
§ 8.50 Дополнения к операторному методу.
1. Для перехода от изображения F(p} к функции времени /(/) может быть использовано обратное преобразование Лапласа:
v+ y <»
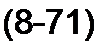jF(p)e/,/ dp.
V- J 00
Функция F(p) аналитична в области Re р > v и стремится к нулю при |р|-> оэ. При практическом использовании этой формулы интеграл по бесконечной прямой, параллельной оси ординат, заменяют контурным интегралом, охватывающим все полюсы функции F(p):
/(') =
Полюсами называют значения р, при которых F{p) обращается в бесконечность. В том случае, когда F(p)= /V(p)/полюсами являются корни уравнения Л/(р) = 0. В теории функций комплексного пере-
менного доказывается, что правая часть формулы (8.72) равна сумме вычетов (Res) подынтегральной функции во всех ее полюсах, т. е.
 | |||
 | |||
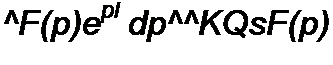
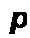