6. Дифференцирование в области изображений. Если F{p}~ то dF(p) . r . . г-
------- -^ = 1 f(t). Доказательство:
dp
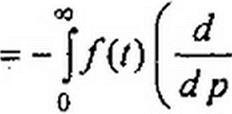 | |||||||||||||
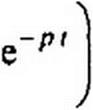 | |||||||||||||
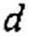 | |||||||||||||
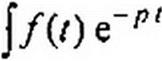 | |||||||||||||
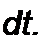 | |||||||||||||
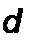 | |||||||||||||
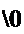 | |||||||||||||
Например, если /0) = е“а'; F{p)~------------------------------------------------------------- ; то
/? + а
. -а/ dF(p} 1
Л —к ■ । ।
dp (р + а)1
7. Интегрирование в области изображений. Если при / > 0 /(/) и
СО
f(t)/t преобразуемы по Лапласу и ^F(p)dp существует, то
р
Доказательство:
| о \о |
| -р> |
| d р dt |
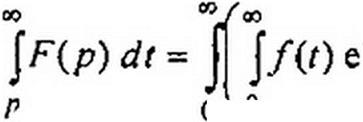
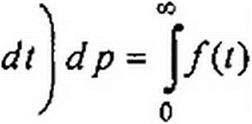
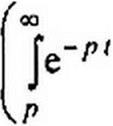
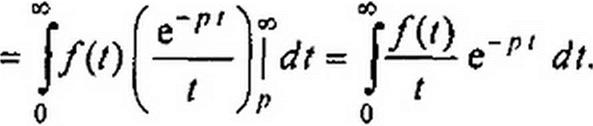
| Например, если /(0 = 1- е-а 1 |
| 1 -е~а' |
| р(р + а) |
| (а > 0), |
| ^(/0 = |
| а Р(Р + а) ’ |
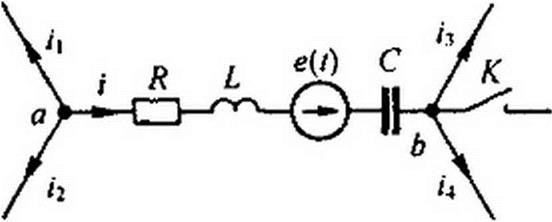
| § 8.41. Закон Ома в операторной форме. Внутренние ЭДС. На рис. 8.28 изображена часть сложной разветвленной электрической цепи. Между узлами а и Ь этой цепи включена ветвь, содержащая Л, £, С и источник ЭДС е(/). Ток по ветви обозначим через /. |
| Рис. 8.28 |
| Замыкание ключа К в схеме приводит к переходному процессу. До коммутации ток i = /(0_) и напряжение на конденсаторе ис = Выразим потенциал точки а через потенциал точки b для послекоммутаци- онного режима: |
| <?а=Фл+«С+и/.+ЫЛ »ab = Фо — ~ U R + и1. + иС ~ |
| Вместо и{ запишем н<-(0) + — р’ dt. Тогда С о |
| di —, вместо ис dt |
| соответственно |
| 9 • 1 / uah = i R + L + wc(0) + — p dt - e(0. |
| (8.46) |
| ' К уравнению (8.46) применим преобразование Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений. Каждое слагаемое уравнения (8.46) заменим операторным изображением: вместо i R запишем RI(p)', вместо uah — иаЬ(р}\ |
| ^■ = ЬрГ(р)~И(0); dt |
| uc(Q)^ |
| e(t) = E(p). |
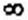
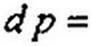
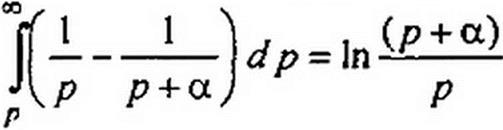
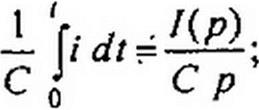
В результате найдем
и al, (Р) = Кр) я + р L + - L 1(0) + - Е(р). (8.47)
к Ср) Р
Смысл проведенного преобразования состоит в том, что вместо дифференциального уравнения (8.46) получили алгебраическое уравнение (8.47), связывающее изображение тока 7(р) с изображением ЭДС Е(р) и изображением напряжения Uah(p")‘ Из уравнения (8.47) следует, что
Ual,(p)+Li(.0)-^ + E(p)
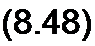 Кр)----------------------- г—2------------------
Кр)----------------------- г—2------------------
Z(p)
где Z(p) = R + р L +-------------- операторное сопротивление участка цепи
С р
между точками а и Ь. Структура его аналогична структуре комплекса сопротивления того же участка цепи переменному току, если у® заменить на р (см. с § 8.13).
Как указывалось в § 8.13, комплексное число р = а + j b может быть записано в виде р = j (b- j а) = j Q, где Q = b - j а — комплексная частота; Z(p) = Z(J Q) — сопротивление, оказываемое рассматриваемой цепью воздействию U e,Q/ = LJ ер1у подобно тому как Z(j со) есть сопротивление, оказываемое воздействию 0 eJMl. Поэтому Z(p) называют сопротивлением на комплексной частоте.
Уравнение (8.48) может быть названо законом Ома в операторной форме для участка цепи, содержащего ЭДС. Оно записано при ненулевых начальных условиях.
Слагаемое L i(0) представляет собой внутреннюю ЭДС, обусловленную запасом энергии в магнитном поле индуктивной катушки вследствие протекания через нее тока /(0) непосредственно до коммутации. Слагаемое и(-(0)/ р представляет собой внутреннюю ЭДС, обусловленную запасом энергии в электрическом поле конденсатора вследствие напряжения на нем wc(0) непосредственно до коммутации.
В соответствии с формулой (8.40) на рис. 8.29 изображена операторная схема замещения участка цепи рис. 8.28. Операторные сопротивления ее Л, р L, 1/ (С р}. Как следует из формулы (8.48), внутренняя ЭДС L ЦО) направлена согласно с направлением тока 1(р), внутренняя ЭДС L7c (0)/ р —встречно току /(р).
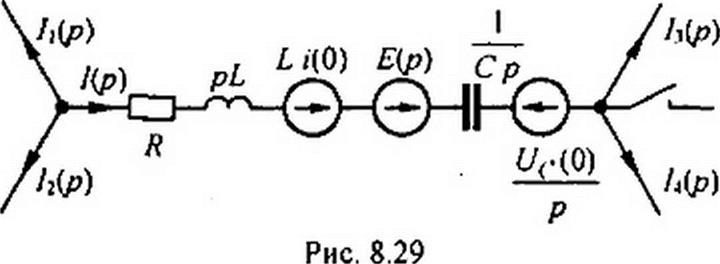 |
В частном случае, когда на участке ab отсутствует ЭДС е(0 и к моменту коммутации /(0)-0 и ис(0) = 0, уравнение (8.48) приобретает более простой вид:
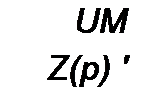 | ||||||||||||||||||||||
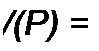 |  | |||||||||||||||||||||
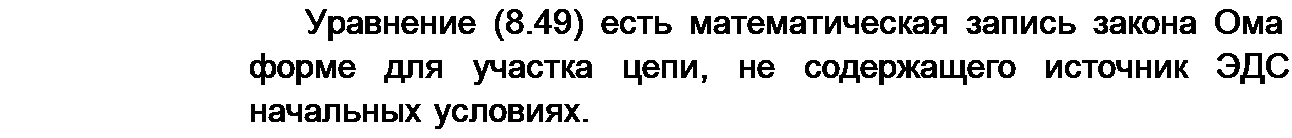 | ||||||||||||||||||||||
 | ||||||||||||||||||||||
 |  | |||||||||||||||||||||
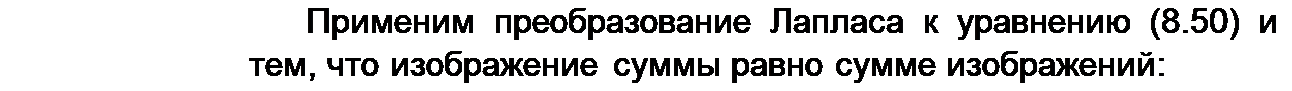 | ||||||||||||||||||||||
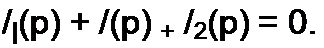 | ||||||||||||||||||||||
 | ||||||||||||||||||||||
 | ||||||||||||||||||||||
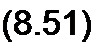 | ||||||||||||||||||||||
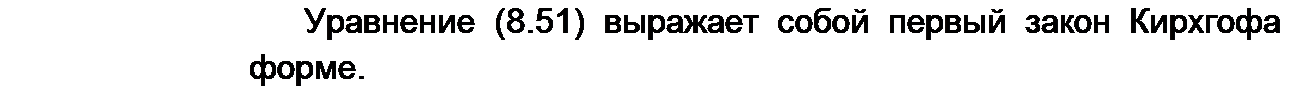 | ||||||||||||||||||||||
 | ||||||||||||||||||||||
 | ||||||||||||||||||||||
|
 | |||
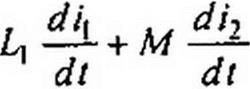 | |||
|
 |
 | |||
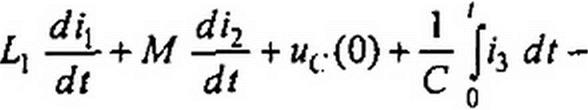 | |||
|
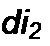 | |||
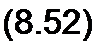 | |||
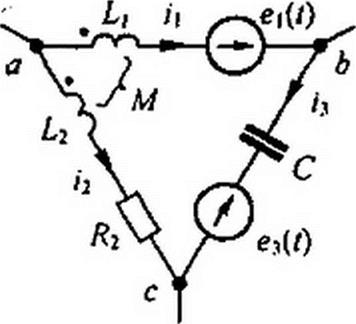
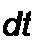 dt
dt
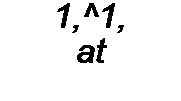 | |||||||
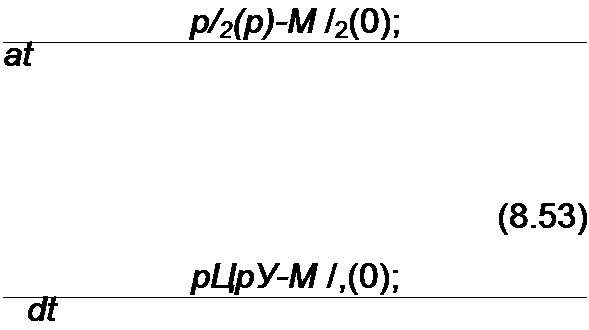 | |||||||
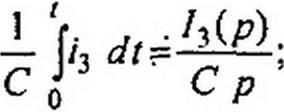 | |||||||
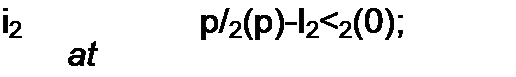 | |||||||
Каждое из слагаемых (8.52) заменим операторным изображением:
^i(O?=£i(p); e3(/)=£3(p).
Подставив (8.53) в (8.52), объединим слагаемые с /](р), /2(р), ^(р), перенесем в правую часть u(-(0)/ р, L} ^(О) и другие внутренние ЭДС. В результате получим
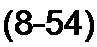 Л (р) z} (р) + /2 (р) z2 (р)+Л (р) z3 (р) =
Л (р) z} (р) + /2 (р) z2 (р)+Л (р) z3 (р) =
~ Ex(p)~E3(P) + Ew(p),
где
Z|(p)«p(£1-Л/); Z2(p)= р(Л/-£2); Z3(p) = I/(С р);
£(р) = (£, - Л/) (0) + (Л/ - £2) /2(0) - иг(0)/ р.
В более общем виде уравнение (8.54) можно записать так:
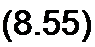 £*(/>) = ££*(/>)•
£*(/>) = ££*(/>)•
Уравнение (8.55) представляет собой математическую запись второго закона Кирхгофа в операторной форме. В состав Ек(р) в общем случае входят и внутренние ЭДС.
§ 8.44 Составление уравнений для изображений путем использования методов, рассмотренных в третьей главе. Из уравнений, составленных по законам Кирхгофа для мгновенных значений, вытекают соответствующие уравнения для изображений.
Уравнения для изображений по форме аналогичны уравнениям, составленным для той же цепи с помощью символического метода для комплексов токов и напряжений.
Но если каждому уравнению для комплексов отвечает соответствующее уравнение для изображений, то все основанные на законах Кирхгофа приемы и методы составления уравнений (методы эквивалентного генератора, контурных токов, узловых потенциалов, наложения и т. п.) можно применить и при составлении уравнений для изображений.
При составлении уравнений для изображений ненулевые начальные условия учитывают путем введения «внутренних» ЭДС, обусловленных начальными токами через индуктивные элементы и начальными напряжениями на конденсаторах.
§ 8.45 Последовательность расчета операторным методом. Расчет операторным методом состоит из двух основных этапов:
1) составления изображения искомой функции времени;
2) перехода от изображения к функции времени.
На нескольких примерах покажем, как производится первый этап. Второй этап будет рассмотрен в § 8.47.
Пример 88. В схеме на рис. 8.31 при нулевых начальных условиях замыкают ключ. Составить операторные изображения токов и , пользуясь методом контурных токов.
Решение. Направления контурных токов i} । и i22 показаны на схеме.
Имеем:
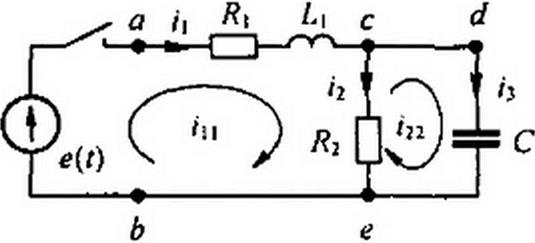
|
i| ( Я, + £] 11 + R2(i\ । - bj )= e (f)>
а {
Переходим к изображениям:
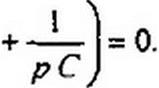 |
|
/] [(р) (р Lx + /?j + Л2)- /22(р) /?2 = £(р);
Совместное решение двух уравнений с двумя неизвестными даст:
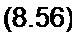
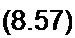 , £(/>)(!+Л2 С р)
, £(/>)(!+Л2 С р)
1 ] ] \Р > = 7------------------ >
р R2 С + р (Л| R2 С + Lx) + /?[ + R2
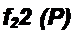 ____________ Е(Р) ^2 Ср______________
____________ Е(Р) ^2 Ср______________
р~ R2 Lx С + р (/?, /?2 С + £|) + + /?2
Изображение контурного тока Цх(р} равно изображению тока 1х(р\ изображение /2г(Р)— изображению /з(р). В (8.56) и (8.57) Е(р) есть изображение ЭДС е(О- Если е(/) = £, то Е(р)-Е!р. если e(t) = Е„ sin(o/ + ф), то Е(р) = Ёт--------------------------------------------------------------------------------- *---------------------------------------------------------------------------------- и т. д.
р~ j со
Пример 89. Составить операторные изображения токов и /j схемы на рис. 8.31, пользуясь законом Ома и Кирхгофа.
Решение. Так как в схеме нулевые начальные условия и нет магнитно-связанных индуктивных катушек, то составить уравнение можно проще, чем по методу контурных токов.
| Изображение тока |
| £(р) Z 0^P)' |
| где ZBX(p) — входное сопротивление схемы в операторной форме относительно зажимов ab. Его определяют так же, как входное сопротивление для переменного тока, только j со заменяют на р. Входное операторное сопротивление |
| z »x(p) = R\ + Р Л + Следовательно, |
| pl Ц С /?2 + р (L| + /?) О + + /?2 1 + R-> С р |
| Л(р) = |
| Е{р} _____________ ц^)(1+ /?2 С р)____________ Z sx(Р) Р^ Ь С R2 + Р ^1 ^2 С)+ ^2 |
| (8.58) |
| уравнение (8.58) совпадает с уравнением (8.56). Найдем изображение Л(/’) С этой целью выразим !^р) через 1}(р) и операторные сопротивления второй и третьей ветвей. Воспользуемся аналогией с переменным током. Для переменного тока |
| Л = /)------------ —--------- • ’ 1 /?2 +1/(/со С) |
| Следовательно, |
| /?2 Л,+1/(С Р)' |
| Если в последнее выражение подставить 1}(р) из уравнения (8.58), то будет получено уравнение (8.57). Таким образом, безразлично, каким способом составлять изображение токов: результат будет одинаков. |
| Пример 90. Для схемы (см. рис. 8.31) составить изображение напряжения на зажимах се, если считать, что начальные условия нулевые (как в примере 89). Решение. Изображение напряжения на зажимах се равно произведению изображения тока на операторное сопротивление конденсатора: |
| </«(/>)• 71— с р |
| _____________ Е(р> я2______________ р~ R2 L] С + р (/?] /?2 С + L\) + R\ + /?2 |
| (8.59) |
| § 8.46. Изображение функции времени в виде отношения 7V(p) / М(р) двух полиномов по степеням р. Для тока /п(р) в примере 89 если принять Е(р)~ Е/р, то |
| ЛЧр) = Е(1 + R2 С р); М(Р) = (Р2 R2 L'C + p(R}R2C + L}) + R,+R2)P. Если в том же примере принять е(/) - Ет sin(w/ + ф)> то |
| и ^(p)=Ёт а + r2 с ру, |
| М(р) — (р — j со) (р_ /?7 L\ Ср(/?] R2 С + ) + /?| + R2). |
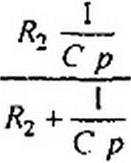
|
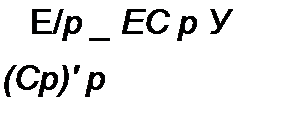 | |||
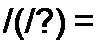 | |||
Обозначим высшую степень оператора р в полиноме 7V(p) через п, а высшую степень р в полиноме М(р) — через т.
Часть корней уравнения М(р) = 0 обусловлена характером измене-
ния во времени возмущающей силы, воздействующей на систему; остальные корни обусловлены свойствами самой цепи, ее конфигурацией и значениями параметров.
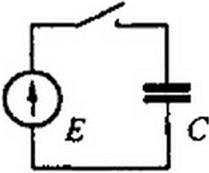
Если исключить из рассмотрения сверхпроводящие электрические цепи, то во всех физически осуществимых электрических цепях при воздействии любых ЭДС всегда пет. Лишь для физически неосуществимых электрических цепей степень п может оказаться равной т. Пример цепи, для которой степень п равна степени
т, дан на рис. 8.32. Если считать, что сопротивление проводов и внут
реннее сопротивление источника нулевые, то
§ 8.47. Переход от изображения к функции времени. В § 8.45 указывалось, что вторым этапом расчета переходных процессов с помощью операторного метода является переход от изображения к функции времени. Эту операцию можно осуществить различными путями.
Первый путь состоит в применении формул соответствия между функциями оператора р и функциями времени I. Часть формул соответствия приведена в § 8.39. В научной литературе имеются специальные исследования, содержащие большое число формул соответствия (1518), охватывающих все возможные практические задачи. Формулами соответствия рекомендуется пользоваться в том случае, когда среди корней уравнения М(р) = 0 есть несколько одинаковых (кратные корни).
Второй путь состоит в применении так называемой формулы разложения. Формула разложения в § 8.49 выведена исходя из предположения, что уравнение M(p)-Q не имеет кратных корней (при наличии кратных корней формула разложения записывается иначе — см. § 8.50).
Третий путь — непосредственное применение формулы обратного преобразования Лапласа с использованием теории вычетов (см. § 8.50).
Формулой разложения широко пользуются на практике, и ее принято рассматривать как основную формулу для перехода от изображения к функции времени.
Рассмотрим два примера на применение формул соответствия, а затем — после рассмотрения вопроса о разложении сложной дроби на простые — перейдем к выводу формулы разложения.
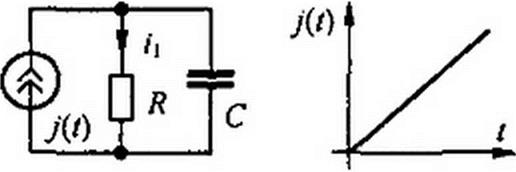
Пример 91. В схеме рис. 8.33, а ток источника тока линейно нарастает во времени: У(г) = 2,5 / А (рис. 8.33, б); /? = 50 кОм. С = 2 мкФ. Определить закон изменения во времени тока /) через резистор Я.
Решение. Изображение тока j\t) равно 2,5/р2 (см. соотношение 12. § 8.39).
Сопротивление параллельно соединенных R, С: Z(p) =--------------------------------------------------------------------------------- .
 | |||||
 | |||||
 | |||||
|
Изображение тока через R
l(n x Ap)Z(p)_ 2,5 1
W} ~ R ’ RC р2(р + а)'
(0-2,5 (г-0,08 (1-е”'2,5')) А,
где а -[f(R С) = 12,5 с"1.
Согласно соотношению 8, § 8.39,
р (р + а) а а
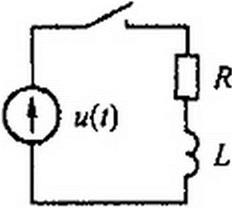
Пример 92. В схеме на рис. 8.34 u(t) = 100е~<7' В, где а = 0,5с-1; /? = 20м;
Д = 4Гн. Найти i = и «д =/(/), а также значения / и uL при / = 1с.
Решение. Согласно соотношению 2, § 8.39. функции е‘4 соответствует изображение 1/(р + о). Следовательно.
(Др) = -^-; Z(p) = R + pL.
р + а
и = 100 = юо-1
Zip) (p + a)(pL + R) L(p + a}{p + b)'
-^ = 25А7с; h = - = 0.5 = a; /(р) = 25----------------------------- г.
L L (р + а)
По соотношению 5, $ 8.39 ----------- !—-=/е'в/. Поэтому /(/) = 25/,е’0,5г
(Р + а)2
Напряжение на L:
и, =£ —= 100 е^15 (1~0.5)= 20.3 В.
di
При / = !с / = 25-1 е-0 5 = 15,15 А; и, = ЮОе'0-’ (I-0,5) = 30,3 В.
§ 8.48. Разложение сложной дроби на простые. Из курса математики известно, что дробь
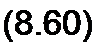 ?/(х) _ ап хп + ап_| х”'1 + ... + Д| x + aQ
?/(х) _ ап хп + ап_| х”'1 + ... + Д| x + aQ
М(х) Ьт хп' +Ь„Л хп,~' 4-... + ^ х + 60
при условии, что п<т и полином Л/(х)-0 не имеет кратных корней, может быть представлена в виде суммы простых дробей:
|
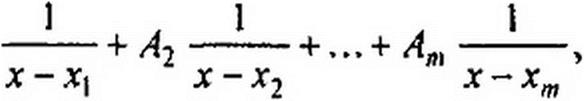
|
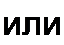 |
*(x) _ л 1
------- ~ / А »
W) Л?) х-хк
где хк — корни уравнения М(х) = 0.
Для определения коэффициента А} умножим обе части уравнения (8.61) на (х-хД В результате получим
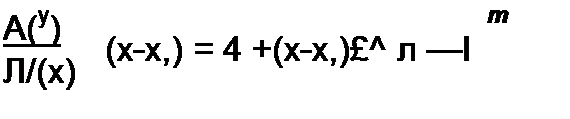 | |||||
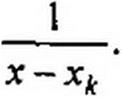 | |||||
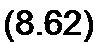 | |||||
Рассмотрим выражение (8.62) при х->хР Правая часть уравнения равна а левая представляет собой неопределенность, так как множитель (x-Xj) при х —> Х| равен нулю и знаменатель Л/(х) при x = Xj также равен нулю (х, есть корень уравнения Л/(х) = 0).
Раскроем неопределенность по правилу Лопиталя. С этой целью производную от числителя разделим на производную от знаменателя и найдем предел дроби:
х-х, Л/(х) х-»г, М\х) М\х}У
где Л/'(х)—производная от М(х) по х, A/'(xj)— значение Л/'(х) при х = х}, Л<(х})—значение Л/(х) при х = хР
Следовательно, из (8.62) при x->xt получаем
/V(xl)/M'(x!) = J1, (8.63)
или
л, == JV(x,) / ЛГ (xt). (8.64)
Аналогично
Ак = ^{хк}/М\хк\ (8.65)
Таким образом,
*(*) = N(Xi) I , N(x2) 1 t г ^хда) 1
Л/(х) Л/'(Х|) х-Х] Л/'(х2)х-х2 Л/'(хот)х-хт’
или
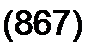 | |||
 | |||
Пример 93. Найти коэффициенты разложения дроби 1/ (х2 +5х + 6). Решение. Корни уравнения Л/(х) = 0:
xt = -2, х2 = -3;
Л/'(х) = 2х + 5; Л/'(Х|) = -2-2 + 5 = + 1; ЛГ(х2) = -1, Мх,) = Л'(х2) = 1.
По формуле (8.65)
=^х|)/Л/'(х1 ) = !/(+!) =+1; Л2=^х2)/Л/'(х2) = -1.
§ 8.49. Формула разложения. Переход от изображения N(p)! М(р) к функции времени часто производят с помощью формулы
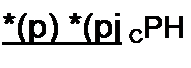 | |||
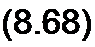 | |||
которую называют формулой разложения.
Левая часть формулы является функцией р, правая часть — соответствующей ей функцией времени /.
Вывод формулы можно осуществить следующим образом. Пусть изображение какой-либо функции времени, например тока,
/(p)=N(p)/M(p).
Для получения тока как функции времени /(/) представим сначала N(p)/М(р) в виде суммы простых дробей — разложим N(p)l М(р). С этой целью в формуле (8.67) заменим х на р:
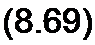 '<-> ■ S ■ i —
'<-> ■ S ■ i —
М(р) »=|Л/(й)р-рЛ
Перейдем от изображения к оригиналу. Оригиналом левой части является /(г). Оригинал правой части равен сумме оригиналов ее слагаемых.
Учтем, что множители У(р4)//V/'(p-.) у слагаемых суммы правой части (8.69) есть постоянные числа (не функции р!). Кроме того, функциями р в правой части являются только множители 1/(р- р*); им соответствуют функции времени вида еРк' (см. формулу (8.34)). Поэтому
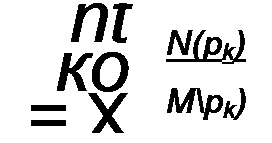 | |||||
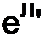 | |||||
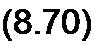 | |||||
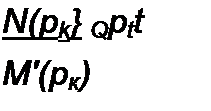
Переход от изображения (функции р) к оригиналу (функции /) с помощью формулы разложения (8.70) основан на том, что изображение представлено в виде суммы простых дробей ^(Рк) !—, а оригина-
М'(рк) р- рк
лами их являются показательные функции
Число слагаемых ———-е'* равно числу корней уравнения
М \Рк )
Л/(р) = 0. Коэффициенты N(pk}l М\рк) можно сопоставить с постоянными интегрирования дифференциального уравнения (уравнений) цепи в классическом методе расчета.
Если среди корней уравнения Л/(р) = О есть нулевой корень (р - 0), то ему в правой части уравнения (8.70) соответствует слагаемое
е = - Слагаемое //(0)/м(р) представляет собой состав
ляющую искомого тока (напряжения), обусловленную постоянными вынуждающими силами. Если постоянных вынуждающих сил в схеме нет, то N(0)/ М '(0) = 0.
Важно сделать некоторые замечания к формуле (8.70).
1. Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника ЭДС или тока, воздействующего на схему.








