§ 8.34 Изображение показательной функции eat. Вместо /(г) в
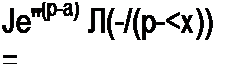(8.31) подставим е“' :
F{p) = Jea' е~р1 dt = fe-'{'”ci) dt = |- о о V
 | |||
 |
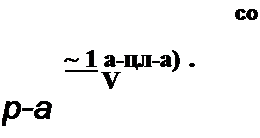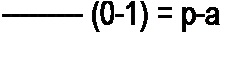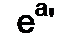
Таким образом,
(8.34)
При выводе формулы (834) (при подстановке пределов) было учтено, что действительная часть оператора р больше, чем а, т. е. а>а. Только при этом условии интеграл сходится.
Из формулы (834) вытекает ряд важных следствий. Положив в ней а = у со, получим
eJ“>' = ! . (8.35)
P-J®
Формула (835) дает возможность найти изображение комплекса синусоидального тока:
/ pjCw'+v) _ j -jut
С этой целью обе части (835) умножим на постоянное число }т :
. (8.36)
Р~ J со
Аналогично, изображение комплекса синусоидального напряжения
(837)
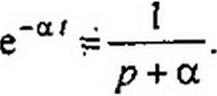Функции e“af соответствует изображение 1/(р + а):
(8.38)
§ 835. Изображение первой производной. Известно, что функции f(f) соответствует изображение F(p'). Требуется найти изображение первой производной df{t)tdt, если известно, что значение функции /(О при / = 0 равно /(0).
Подвергнем функцию df(t)ldt преобразованию Лапласа:
Л = Je"'” rf(/(0). о
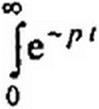Интегрирование произведем по частям jw dv = и v - j v du. Обозначив e~pl = u и df(t)ldt = dvt получим
</(/(0) = e’" 7(0?-f/(0 о 0
e''” 7(0|| =0-/(0) = -/(<>), о
f/(O de"' = p ]/(o e'" dt^p F(p).
0 0
 | |||||||
 | |||||||
 | |||||||
 | |||||||
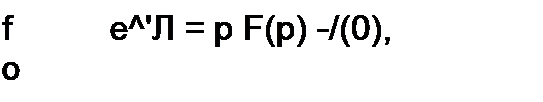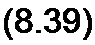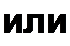</W^pF(p)-/(0). (8.40)
§ 8.36 Изображение напряжения на индуктивном элементе. Изображение тока / равно /(р). Запишем изображение напряжения на L: U[ =L—. По формуле (8.40), — = р /(р)-/(0), где /(Ор—значение dt dt
тока i при t - 0~. Следовательно,
Л—-£ р/(р)-Л/(0). (8.41)
di
Если /(0) = 0, то
L^LpUp). (8.42)
at
§ 8.37 Изображение второй производной. Без вывода дадим формулу
 | |||
 | |||
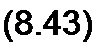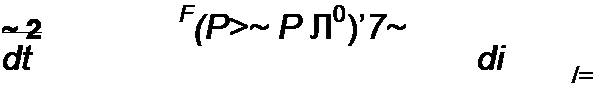Следовательно, изображение второй производной тока /
^Г=р2 /(р) - р/(0) -/'(0).
dr
§ 8.38 Изображение интеграла. Требуется найти изображение фун- /
кции j/(r)d7, если известно, что изображение функции /(г) равно о
F(p). ,
Подвергнем функцию j/(/)t// преобразованию Лапласа:
о
 |
|
 |
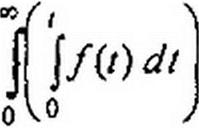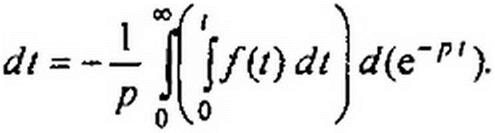‘•Для сокращения записи вместо Д0_) пишем ДО); ДО) может быть и положительной, и отрицательной величиной; ДО) положительно, когда направление тока совпадает с произвольно выбранным положительным направлением послекоммутационного тока в индуктивном элементе L.
(
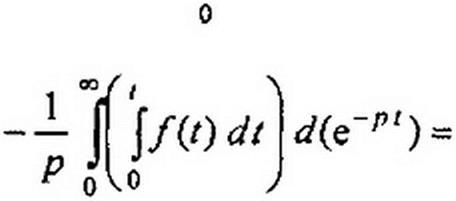
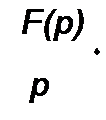Примем j/(z) dt - w, c/(e'/’f) = dv и возьмем интеграл по частям:
- i/(t)dt е~р'|+-------------------------------
Р U Jo Р
Первое слагаемое правой части при подстановке верхнего и нижнего пределов обращается в нуль. При подстановке верхнего предела нуль получается за счет ранее наложенного ограничения на функцию f(t) (см. § 8.32) функция ДО если и растет с увеличением Г, то все же медленнее, чем растет функция е6", где а — действительная часть р. При подстановке нижнего предела нуль получим за счет обращения в нуль t
|/(0 dt. Следовательно, если f(t)=F(p), то о
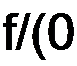dt = ^-. (8.44)
|
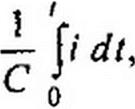
§ 8.39. Изображение напряжения на конденсаторе. Напряжение на конденсаторе ис часто записывают в виде ис р dt, где не указаны пределы интегрирования по времени. Более полной является следующая запись:
"с
где учтено, что к моменту времени t напряжение на конденсаторе определяется не только током, протекшим через него в интервале времени от О до /, но и тем напряжением wf-(0), которое на нем было при 1-0.
]
В соответствии с формулой (8.44) изображение — ji dt равно о
1{р) / (С р), а изображение постоянной ис(0) есть постоянная, деленная на р. Поэтому изображение напряжения на конденсаторе записывают следующим образом:
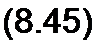_/(р) И(.(0)
*“ ------------------ I
Приведем простейшие операторные соотношения; часть их была выведена ранее, другая дается без вывода:
‘‘Для сокращения записи вместо ир(0_) пишем и((0); «с(®) может быть и положительной, и отрицательной величиной. В формуле (8.45) считают положительной величиной, если направление ur(0) совпадает с произвольно выбранным положительным направлением послекоммутационного тока через конденсатор.
| I) |
| 16) |
| - у = — sh a -а а |
| 2) |
| Fe'a'; |
| 17) |
| 3) |
| =eyw/: |
| 18) |
| - sin a ty а |
| 4) |
| 6) |
| 7) |
| 8) |
| 9) |
| P(P + a) |
| (р + а)2 |
| =teal; |
| —y=(l-ar)e'a'; |
| ------ !------ -е"а' р(р + а)2 а2 |
| 1 е'0' а2 + о2 ’ |
| 19) |
| 20) |
| 21) |
| У^—у = cos a Аш. . |
| (р2 + а2)(р2 + Ь2) Ь2-а2 x(cosa/-cos5/); |
| e"al sin bt; |
| 22) i==6(r); |
| --------------------- —— (а е-°‘ - Ь е’*' (р + а)(р + Ь) а~Ь |
| Ю)----------- :--------- =-^- (р + a)(p + b) а-Ь |
| -hi |
| 11) |
| Р(Р + ^)(Р + Ь) ab 1 е-а,\ b-a b а |
| 23) |
| 24) |
| = Л(^/); |
| 25) |
| 26) |
| a |
| у где Ф — |
| ин- |
| 27) |
| 12) |
| теграл ошибок Гаусса; |
| 13) |
| 28) |
| 14) |
| Р <Р + <0 |
| at 2 |
| е~а1: |
| 29) |
| e'4/’+2A/’ I(ih [р—2 |
| 15) |
| е -а/; п (л-1)! |
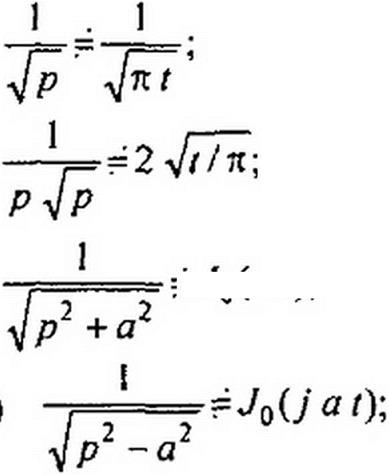
§ 8.40 Некоторые теоремы и предельные соотношения.
1. Теорема смещения в области оригиналов (теорема запаздывания). Если изображение функции /(О равно F(p), то изображение функции /(/-т) равно е“р/ F(p).
Теорема доказывается путем подстановки /(/-т) в формулу преобразования Лапласа и введения новой переменной = dt~dtx,
= е-Р* e -Ph .
Je'" /(z - т) </т = e'*” Je-P'1 /(/,)<//, =е''” F(p). о о
Пример на применение теоремы см. в § 8.60.
2. Теорема смещения в области изображений. Если изображению функции Г(р) соответствует функция /(/), то изображению Г(р-Х) — функция ех' /(/).
Доказательство проводят путем подстановки функции еи /(/) в формулу преобразования Лапласа:
Je~p' eu f^dt=”\e,{p-y'} f(t) dt = F{p-\). о о
Пример 87. Найти оригинал 1/(р + Х)2, если известно, что 1/р2=г Решение: 1/(р + Л.)2=е-х' г.
3. Теорема об изменении масштаба {теорема подобия). Если функции /(/) соответствует изображение F{p), то функции /(АО—изоб-
1 А
ражение — F — .
а \а)
Теорема доказывается следующим образом:
/(a t) dt = - fe * /(а t) d(a O = - Л .
а о а w
4. Нахождение начального значения функции времени /(0+) по изображению функции F(p):
/(0J= hm р F(p).
Это соотношение получим, если в (8.39) р устремим к бесконечности. При этом левая часть (8.39) равна нулю.
5. Нахождение установившегося значения функции времени /(ос) по изображению функции F(p):
/(ос) = fim р F(p).
p-rt
Соотношение получим, если в (8.39) р устремим к нулю и учтем, что
В результате имеем
р/(0 = /(«) - /(0) = lim р F(p) - f(Q), или
/(0) = lim p F(p).
/-><» p-*0
Если искомая функция /(t) а послеком мутационном режиме содержит в своем составе периодическую составляющую (принужденную или свободную), то понятие /(<ю) для нее оказывается неопределенным. Например, не имеет определенного смысла функция sin со/ при / = <». В соответствии с этим к цепям с синусоидальными источниками не следует применять предельное соотношение п. 5. Точно так же не следует пользоваться им для цепей без синусоидальных источников, если эти цепи чисто реактивные и не содержат резисторов. Так, при подключении последовательно соединенных L и С (при нулевых начальных условиях) к единичному напряжению 1(f) по цепи протекает свободная составляющая тока, численно равная 4с IL $in(Z,/JlC). В этом случае определять /(со) как lim р Г(р) также не имеет смысла.