§ 8.7 Начальные значения величин. Под начальными значениями величии (в литературе их называют еще начальными условиями) понимают значения токов и напряжений в схеме при t - 0.
Как уже отмечалось, токи через индуктивные элементы и напряжения на конденсаторах непосредственно после коммутации равны их значениям непосредственно до коммутации. Остальные величины — напряжения на индуктивных элементах, напряжения на резисторах, токи через конденсаторы, токи через резисторы — могут изменяться скачком, следовательно, их значения после коммутации чаще всего оказываются не равными их значениям до коммутации. Поэтому следует различать до- коммутационные и послекоммутационные начальные значения.
Докаммутационными начальными значениями называют значения токов и напряжений непосредственно до коммутации (при/ = 0_); пос- пекоммутационными начальными значениями — значения токов и напряжений непосредственно после коммутация (при / = 0+).
§ 8.8 Независимые и зависимые (послекоммутационные) начальные значения. Для любой схемы после коммутации в ней можно записать уравнения по законам Кирхгофа и из этих уравнений определить значения токов во всех ветвях и напряжений на любых участках схемы в послекоммутационном режиме (при / = 0+).
С этой целью значения токов в ветвях, содержащих индуктивные элементы, и значения напряжений на конденсаторах берут равными тем значениям, которые они имели до коммутации при t - 0_, а остальные токи и напряжения после коммутации при t - 0+ находят из уравнений Кирхгофа, поскольку часть слагаемых в них известна.
Значения токов через индуктивные элементы и напряжений на конденсаторах, известные из докоммутационного режима, условимся называть независимыми начальными значениями.
Значения остальных токов и напряжений при / = 0+ в послекоммута- ционной схеме, определяемые по независимым начальным значениям из законов Кирхгофа, будем называть зависимыми начальными значениями.
§ 8.9 Нулевые и ненулевые начальные условия. Если к началу переходного процесса непосредственно перед коммутацией все токи и напряжения на пассивных элементах схемы равны нулю, то в схеме имеют место нулевые начальные условия. Если же к началу переходного процесса хотя бы часть токов и напряжений в схеме не равны нулю, то в схеме имеют место ненулевые начальные условия.
При нулевых начальных условиях токи в индуктивных элементах и напряжения на конденсаторах начнут изменяться с нулевых значений, при ненулевых условиях — с тех значений, которые они имели непосредственно до коммутации.
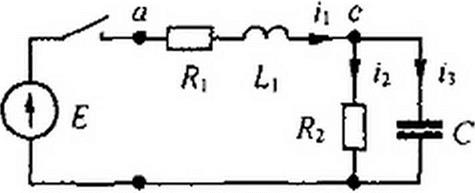
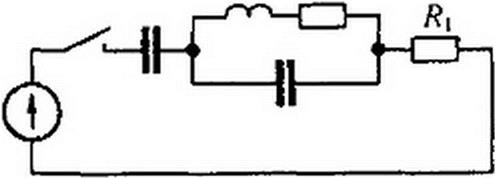
§ 8.10 Составление уравнений дли свободных токов и напряжений. Для послекоммутационной схемы составляют уравнения по законам Кирхгофа для полных токов и напряжений, так же как это делалось и раньше: сначала обозначают токи в ветвях и произвольно выбирают для них положительные направления, затем составляют уравнения по первому и второму законам Кирхгофа. Так, для схемы рис. 8.5 после выбора положительных направлений для токов
имеем:
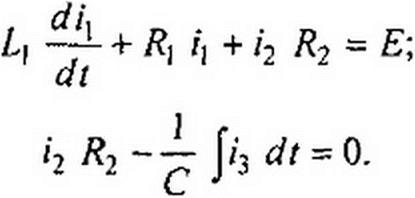 |
|
 |
|
 В этих уравнениях /2» и h — полные токи. Каждый из них состоит из свободного и принужденного токов. Для того чтобы от этой системы уравнений перейти к уравнениям для свободных токов, “освободим” систему от вынуждающих ЭДС (в нашем случае от ЭДС £) и вместо запишем 71св, вместо /2— ^св и т. д. В результате получим:
В этих уравнениях /2» и h — полные токи. Каждый из них состоит из свободного и принужденного токов. Для того чтобы от этой системы уравнений перейти к уравнениям для свободных токов, “освободим” систему от вынуждающих ЭДС (в нашем случае от ЭДС £) и вместо запишем 71св, вместо /2— ^св и т. д. В результате получим:
А св ^2 св ^Зсв 0,
с/л св
— 7~ + /1св + /2ск ^2 = $
^2 св ^2 JhcB ~ 0’
Заметим, что для любого контура любой электрической цепи сумма падений напряжений от свободных составляющих токов равна нулю.
§ 8.11 Алгебраизация системы уравнений для свободных токов. В § 8.3 говорилось о том, что свободный ток представляет собой решение однородного дифференциального уравнения (уравнения без правой части). Как известно из курса математики, решение однородного дифференциального уравнения записывают в виде показательных функций Аер'. Таким образом, уравнение для каждого свободного тока можно представить в виде /св _ А ер/.
Постоянная интегрирования А для каждого свободного тока своя. Показатели же затухания р одинаковы для свободных токов ветвей. Физически это объясняется тем, что вся цепь охвачена единым (общим) переходным процессом.
Составим производную от свободного тока:
 | |||
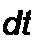 | |||
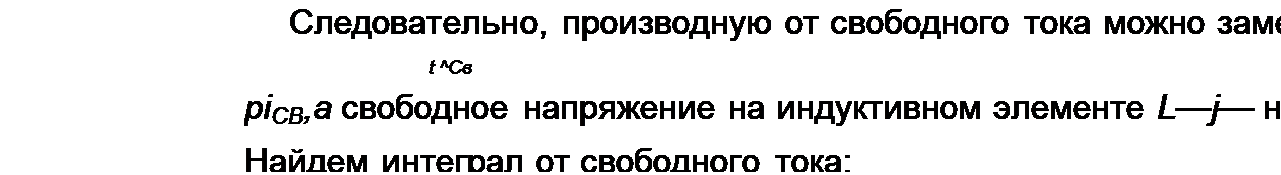 | ||||||||||||||||
 | ||||||||||||||||
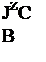 | ||||||||||||||||
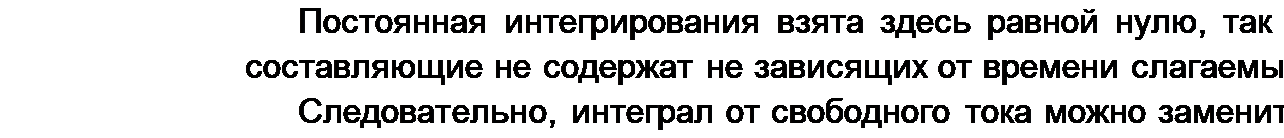 | ||||||||||||||||
 | ||||||||||||||||
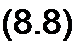 | ||||||||||||||||
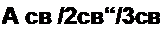 | ||||||||||||||||
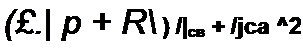 | ||||||||||||||||
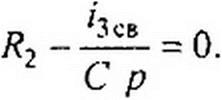 | ||||||||||||||||
|
Уравнения (8.8) представляют собой систему алгебраических уравнений относительно /1СВ’ /2св> бсв и, в отличие от исходной системы, не содержат производных и интегралов.
Переход от системы линейных дифференциальных уравнений к системе алгебраических уравнений называют алгебраизацией системы дифференциальных уравнений для свободных токов. Можно сказать, что система (8.8) есть результат алгебраизаиии системы дифференциальных уравнений (8.7).
§ 8.12 Составление характеристического уравнения системы. Число алгебраических уравнений равно числу неизвестных свободных токов. Положим, что р известно (в действительности оно пока не найдено и будет определено в дальнейшем) и решим систему (8.8) относительно /|св’ ^2 св И /.Зев •
_ Д) . __ Д>. . _ Дз
/] св “ — ’ /?св ’ /)св “ . 5
Д Д Д
где Д— определитель системы. В рассмотренном примере
-I -1
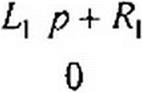 R2 О
R2 О
r2 -i/(Cp)
Определитель Д, получим из выражения для определителя Д путем замены первого столбца правой частью уравнений (8.8):
-1 -1
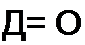 r2 о
r2 о
*2 -У (Ср)
Определитель Д2 получим из выражения для Д путем замены второго столбца правой частью системы (8.8) и т. д.
Так как в правой части системы (8.8) находятся нули, то в каждом определителе Д1? Д2 и Д3 один из столбцов будет состоять из нулей.
Известно, что если в определителе один из столбцов состоит из нулей, то этот определитель равен нулю. Следовательно,
Д, =0, Д2=0, Д3=0.
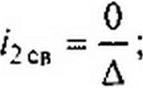 Из физических соображений ясно, что каждый из свободных токов не может быть равен нулю, ибо в этом случае не будут выполнены законы коммутации. Однако из предыдущего следует, что
Из физических соображений ясно, что каждый из свободных токов не может быть равен нулю, ибо в этом случае не будут выполнены законы коммутации. Однако из предыдущего следует, что
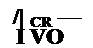 о * д’
о * д’
Свободные токи могут быть не равны нулю в том случае, когда определитель системы
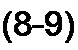 Д = 0.
Д = 0.
Таким образом, определитель Д алгебраизированной системы уравнений должен равняться нулю.
Уравнение Д = 0 называют характеристическим уравнением. Единственным неизвестным в нем является р.
Пример 75. Используя уравнение (8.9), составить характеристическое уравнение для схемы (см. рис. 8.5) и найти его корни.
Решение.
+• Я2 (L| р + Я]) + * Д| = 0
С* х I г 4
Р Ср
или а
р Rz С + р Ri С + L\) + + R?
• -------------- '-------------- ------ — 1л
С р
Если дробь равна нулю, то равен нулю ее числитель. Следовательно,
р2 Я, 4| C+p(R} R2 C+LJ + Я] +Я2 =0. (8.(0)
Корни квадратного уравнения
-(Я! Я, С + /.1)±3/(Я, R2 Сч-Lj)2 -4(Я, + Я2)Я2 L] С
Р'’2 = 2 Я2 L, С ' (8’Н}
В начале § 8.11 говорилось о том, что решение для свободного тока берется в виде А ер‘. Если характеристическое уравнение имеет не один корень, а несколько, например я, то для каждого свободного тока (напря- п
жения) нужно взять ePk 1.
k=\
Пример 76. Найти корни характеристического уравнения схемы на рис. 8.4, а при: 1)С = I мкФ; 2) С= 10 мкФ; 3) С - 100 мкФ; /?1 = Й2 =100 Ом; £, = I Гн.
Решение. 1) При С ~ 1 мкФ
/?[ /?2 С + £( =100-100 110’6 + 1 = 1,01;
4(/?j +/?2)/?2 £, С = 4-200-100-Ю’6 =0,08;
2 Я2 £, С - 2 -100-10’6 = 2-10-4;
-l,01±Jl.012 -0,08 . ,
р, о = у-------------------------------- ; Р|=-250 с-1; р, =-9850 с’1.
2 ЛО’4
2) При С~ 10 мкФ Р] =-230 с’1; р2 - -870 с1.
3) При С= 100 мкФ р( =-100 + 100 /; Р2 =-100-100 j.
§ 8.13 Составление характеристического уравнения путем использования выражения для входного сопротивления цепи на переменном токе. Характеристическое уравнение для определения р часто составляют более простым способом, чем обсуждавшийся в предыдущем параграфе. С этой целью составляют выражение входного сопротивления двухполюсника на переменном токе (обозначим его Z(y со)), заменяют в нем j оо на р (получают Z(p)) и приравнивают Z(p) к нулю.
Уравнение Z(p) = 0 совпадает с характеристическим. Такой способ составления характеристического уравнения предполагает, что в схеме отсутствуют магнитно-связанные ветви. Если же магнитная связь между ветвями имеется, то предварительно следует осуществить развязывание магнитно-связанных ветвей (см. § 3.41).
Поясним сказанное. Как отмечалось в § 2.15, если для некоторой цепи
на постоянном токе составить систему уравнений по методу контурных токов, то входная проводимость относительно w-ветви = Ди / Д, а входное сопротивление /?П( = Д/Дш. Для режима синусоидального тока
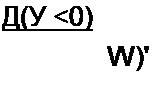 | |||
 | |||
Комплексное число p~a + jb в соответствии с § 8.41 представим в виде р- j (b~ j а) - j Q, где Q — комплексная угловая частота. Сопротивление Z(p) — это сопротивление цепи на комплексной частоте; Z(y to) — это частный случай Z(p), когда Q = <о. Имея это в виду, запи
шем
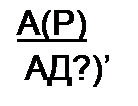 | |||
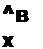 | |||
где Д(р)— определитель системы уравнений, составленных по методу контурных токов.
Таким образом, уравнение = имеет те же корни, что и
уравнение Д(р) - 0.
При составлении Z(/?) следует учитывать внутреннее сопротивление источника питания.
Характеристическое уравнение можно составить так же, взяв за основу не метод контурных токов, а метод узловых потенциалов. В этом случае следует приравнять к нулю определитель матрицы узловых проводимостей, полагая при составлении матрицы один из узлов схемы заземленным.
Пример 77. Для схемы рис. 8.5 составить характеристическое уравнение.
Реше н и е. Входное сопротивление относительно зажимов ab при переменном токе
Заменим в нем уо на р и приравняем его к нулю:
Отсюда
р“ Ly С Ri + р (Lf + /?| С) + /?| + /?2
I + р2С р
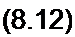 или
или
р~ L] С /?2 + р (£| + /?1 /?2 С ) + /^| + /?? = 0.
Уравнение (8.12) совпадает с уравнением (8.10). составленным иным путем, и получено оно с помощью выражения для входного сопротивления первой ветви схемы (см. рис. 8.5) относительно зажимов ab. Точно такое же уравнение можно получить, если записать выражение для входного сопротивления любой другой ветви.
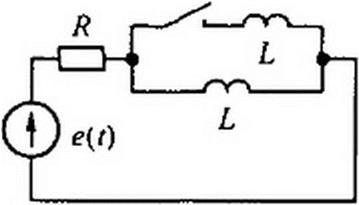
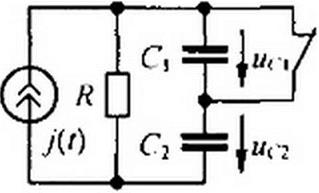
Следует иметь в виду, что во избежание потери корня (корней) нельзя сокращать Д(р) и АДр) на общий множитель, если он имеется. Однако на общий множитель р сокращать Д(р) и А*(р). как правило, возможно, но не всегда. Сокращение на р допустимо для схем, в которых исследуемая величина из физических соображений не может содержать незатухающую свободную составляющую Если же исследуемая величина в рассматриваемой схеме может иметь незатухающую свободную составляющую, то сокращать числитель и знаменатель Z(p) на р (терять корень р - 0) нельзя. Для иллюстрации недопустимости сокращения на р рассмотрим два примера. В послекоммутаиионной схеме (см. рис. 8.6. а) имеется контур из индуктивных элементов, активное сопротивление которого равно нулю. В нем теоретически может протекать незатухающая свободная составляющая тока, которая не будет учтена а решении, если сократить числитель и знаменатель Z(p) = Я? Р.£) на р з схеме на рис. 8.6, б, дуальной схеме на рис. 8.6, а после 2 р L
|
|
коммутации на конденсаторах возможно возникновение равных по значению и противоположно направленных незатухающих свободных составляющих напряжений. Свободный заряд каждого конденсатора не сможет пройти через сопротивление R, так как этому мешает второй конденсатор с противоположно направленной незатухающей свободной составляющей напряжения.
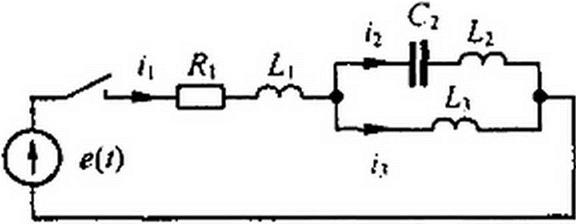
Для схемы на рис. 8.6, б характеристическое уравнение получим, приравняв к нулю входную проводимость относительно зажимов источника тока:
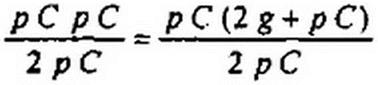 |
|
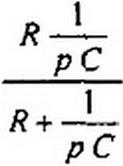
|
|
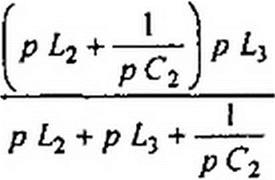 |
|
где g = I / /?.
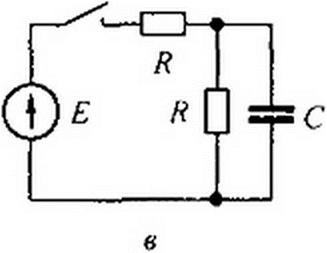
В качестве примера цепи, для которой можно сокращать числитель и знаменатель Z(p) на р, приведем схему на рис. 8.6, в. Для нее
RC p(RC р + 2) _ R(RC р + 2)
Cp(RCp + V) RCp + \
§ 8.14 Основные и неосновные зависимые начальные значения. Для сложных схем со многими накопителями энергии число независимых начальных значений (начальных условий) может оказаться больше, чем порядок характеристического уравнения, и, следовательно, больше числа постоянных интегрирования. В этом случае при определении постоянных интегрирования используем не все независимые начальные значения, а часть из них.
Основными независимыми начальными значениями называют те токи в индуктивных элементах и напряжения на конденсаторах, которые могут быть заданы независимо от других. Остальные независимые начальные значения называют неосновными.
В качестве иллюстрации обратимся к схеме на рис. 8.7. Она содержит три индуктивных элемента и один емкостной. В схеме всего четыре независимых начальных значения (начальных условия):
1)/,(OJ = O; 2) ;2(OJ = O; 3) /3(04) = 0; 4) ur(0 J = 0.
Из них три являются основными и одно — неосновным. Выбор основных значений здесь произволен. Если за основные взять первое, второе и четвертое значения, то неосновным будет третье.
Пример 78. Убедимся в том. что для схемы на рис. 8.7 характеристическое уравнение имеет не четвертую, а третью степень.
Решение. Составляем выражение для входного сопротивления:
Отсюда
(Я, + р £0 (1 + р2 С2 (L2 + Ь>)) + р £3 (1+С2 £j р2) = 0.
Следовательно, характеристическое уравнение имеет третью степень.
§ 8.15 Определение степени характеристического уравнения. Степень характеристического уравнения цепи необходимо уметь оценивать, взглянув на схему, в которой исследуется переходный процесс. Быстрая ориентация позволяет определить трудоемкость предстоящих выкладок и способствует выявлению ошибки, если она возникает при составлении характеристического уравнения.
Степень характеристического уравнения равна числу основных независимых начальных значений в послекоммутационной схеме после максимального ее упрощения и не зависит от вида ЭДС источников ЭДС в схеме.
Упомянутое упрощение состоит в том, что последовательно соединенные индуктивные элементы должны быть заменены одним эквивалентным; конденсаторы, включенные последовательно и параллельно, тоже должны быть заменены эквивалентными.
Применительно к схеме на рис. 8.8, а последовательно включенные L\ и Le2 следует заменить на £, = L{ + ± 2 М, если между ними есть магнитная связь (если нет магнитной связи, то М =0), а конденсаторы ем-

а б
Рис. 8.8
костью CJ, CJ, С4 — на конденсатор емкостью С5 =С4+~~—".
С3 + С3 Начальное значение напряжения на С5 равно начальному значению напряжения на С4.
В результате упрощений схемы рис. 8.8, а получаем схему рис. 8.8, б, в которой два индуктивных элемента и один конденсатор. Все три независимых начальных значения — основные. Следовательно, характеристическое уравнение будет третьей степени.
Обратим внимание на то, что степень характеристического уравнения не зависит от того, имеется ли магнитная связь между индуктивными элементами схемы или она отсутствует.
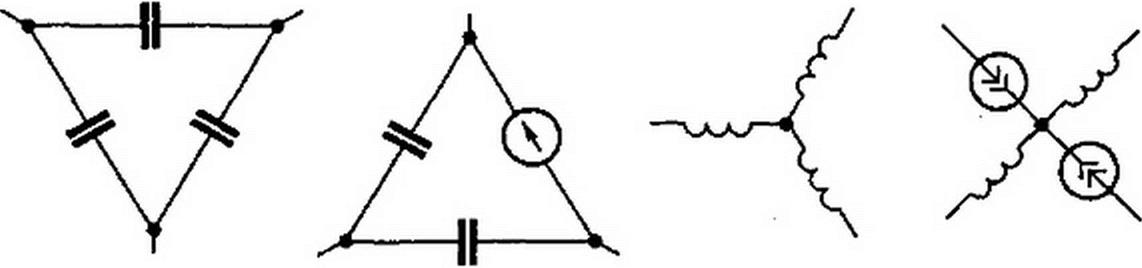
Условимся под емкостным контуром понимать контур, в каждой из ветвей которого имеются либо только конденсаторы (рис. 8.9, а), либо в одни ветви входят только конденсаторы, а в другие — только источники ЭДС (рис. 8.9, б). Положим, что после максимального упрощения схемы
а б в г
Рис. 8.9
в емкостный контур входит и конденсаторов. Если учесть, что по второму закону Кирхгофа алгебраическая сумма напряжений на ветвях контура равна нулю, то только на конденсаторах контура напряжения могут быть заданы произвольно. Условимся под индуктивным узлом понимать узел, в котором сходятся ветви, в каждой из которой имеются индуктивности (рис. 8.9, в), либо часть ветвей с индуктивностями, а другая с источниками тока (рис. 8.9, г). Положим, что в индуктивный узел сходится т-ветвей, содержащих индуктивности. Если учесть, что по первому закону Кирхгофа сумма токов в узле равна нулю, то только в т -1 индуктивностях токи могут быть заданы произвольно.
Обобщенно можно сказать, что после максимального упрощения схемы степень характеристического уравнения может быть определена путем подсчета величины п, + лс -yL -kc, где nL— число индуктивных элементов в схеме; пс — число конденсаторов; ус — число индуктивных элементов, токи в которых не могут быть заданы произвольно; кс — число конденсаторов, напряжения на которых не могут быть заданы произвольно.
Замечания. I. Если схема с источником тока имеет несколько послсдовагельных участков, содержащих параллельно соединенные ветви с R, L, С, то для каждой группы параллельных ветвей будет свое характеристическое уравнение со своими корнями (свободные токи не могут замыкаться через источник тока, поскольку его сопротивление равно бесконечности).
§ 1.1 и в схеме будут иметься так называемые дополняющие двухполюсники (см. § 8.63), содержащие элементы /?, L, С, между которыми выполняются определенные соотношения, то при упрощении схемы они должны быть заменены на эквивалентные им резисторы. Это значительно упрощает выкладки (на эту тему рекомендуется решить пример 30 из вопросов для самопроверки).
§ 8.16 Свойства корней характеристического уравнения. Число корней характеристического уравнения равно степени этого уравнения. Если характеристическое уравнение представляет собой уравнение первой степени, то оно имеет один корень, если второй степени — два корня и т. д. Уравнение первой степени имеет всегда отрицательный действительный (не мнимый и не комплексный) корень.
Уравнение второй степени может иметь: а) два действительных неравных отрицательных корня; б) два действительных равных отрицательных корня; в) два комплексно-сопряженных корня с отрицательной действительной частью.
Уравнение третьей степени может иметь: а) три действительных неравных отрицательных корня; б) три действительных отрицательных корня» из которых два равны друг другу; в) три действительных равных отрицательных корня; г) один действительный отрицательный корень и два комплексно-сопряженных с отрицательной действительной частью.
§ 8.17 Отрицательные знаки действительных частей корней характеристических уравнений. Свободный процесс происходит в цепи, освобожденной от источника ЭДС. Он описывается слагаемыми вида А ер/. В цепи, освобожденной от источников ЭДС, свободные токи не могут протекать сколь угодно длительно, так как в ней отсутствуют источники энергии, которые были бы способны в течение сколь угодно длительного времени покрывать тепловые потери от свободных токов, т. е. свободные токи должны затухать во времени.
Если свободные токи (выраженные слагаемыми ер/) должны затухать (спадать) во времени, то действительная часть р должна быть отрицательной.
Значения функции е где at-x, приведены в табл. 8.1.
Рассмотрим характер изменения свободных составляющих для простейших переходных процессов в цепях с характеристическим уравнением первой и второй степеней.
Если число корней характеристического уравнения больше двух, то свободный процесс может быть представлен как процесс, составленный из нескольких простейших процессов.
Таблица 8.1
| X | е’ | с~г | shx | chx | X | е* | сх | shx | chx |
| 0 | 1.0 | 1,0 | 0,0 | 1,0 | 2,1 | 8,17 | 0,122 | 4,02 | 4,14 |
| 0,1 | ио | 0.905 | 0,10 | Г 1,005 | 2.2 | 9,02 | 0,111 | 4.46 | 4.56 |
| 0.2 | 1,22 | 0,819 | 0,20 | 1.02 | 2.3 | 9.97 | 0,100 | 4.94 | 5,04 |
| 0,3 | 1.35 | 0.741 | 0,30 | 1,04 | 2.4 | 11,02 | 0,090 | 5,47 | 5,56 |
| 0,4 | 1,49 | 0,670 | 0,41 | 1.08 | 2.5 | 12.18 | 0,082 | 6,05 | 6,13 |
| 0.5 | 1,65 | 0,606 | 0,52 | 1.13 | 2,6 | 13.46 | 0,074 | 6,7 | 6,77 |
| 0.6 | 1.82 | 0.549 | 0,64 | 1,18 | 2,7 | 14,88 | 0.067 | 7.41 | 7,47 |
| 0,7 | 2,01 | 0.497 | 0,76 | 1.25 | 2,8 | 16.44 | 0.061 | 8.19 | 8,25 |
| 0,8 | 2,22 | 0,449 | 0.89 | 1,34 | 2.9 | 18,17 | 0,055 | 9,06 | 9,11 |
| 0,9 | 2,46 | 0,407 | 1,03 | 1,43 | 3.0 | 20,08 | 0.050 | 10.02 | 10,07 |
| 1.0 | 2.72 | 0,368 | 1,17 | 1.54 | 3.2 | 24,53 | 0,041 | 12,25 | 12.29 |
| 1.1 | 3.00 | 0,333 | 1.34 | 1,67 | 3,4 | 29.96 | 0,033 | 14,96 | 15,00 |
| 1,2 | 3,32 | 0.301 | 1.51 | 1.81 | 3.6 | 36,60 | 0,027 | 18,28 | 18,31 |
| 1,3 | 3.67 | 0.272 | Z 1,70 | 1,94 | 3.8 | 44.70 | 0,022 | 22,34 | 22,36 |
| 1,4 | 4.05 | 0,247 | 1,90 | 2,15 | 4,0 | 54,60 | 0.018 | 27,29 | 27.30 |
| 1.5 | 4.48 | 0,223 | 2,13 | 2,25 | 4,2 | 66,69 | 0.015 | 33,33 | 33,35 |
| 1.6 | 4,95 | 0.202 | 2,38 | 2,58 | 4.4 | 81,45 | 0,012 | 40.72 | 40,73 |
| 1.7 | 5.47 | 0,183 | 2,65 | 2.83 | 4.6 | 99,48 | 0,010 | 49,74 | 49,75 |
| 1.8 | 6,05 | 0,165 | 2,94 | 3,11 | 4.8 | 121,5 | 0,0082 | 60.75 | 60,76 |
| 1,9 | 6,68 | 0,150 | 3:27 | 3,42 | 5,0 | 184,4 | 0,0067 | 74,2 | 74,21 |
| 2.0 | 7.39 | 0,135 | 3,63 | 3,76 | 6.0 | 400 | 0.0025 | 200 | 200 |
§ 8.18 Характер свободного процесса при одном корке. Когда характеристическое уравнение имеет один корень, свободный ток
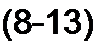 1С| = Яе/" = 4еЛ
1С| = Яе/" = 4еЛ
ще р--а зависит только от параметров цепи, А — от параметров цепи,
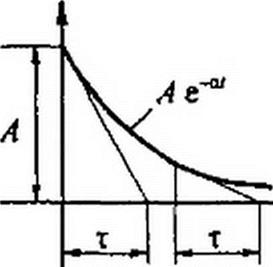
величины ЭДС. Характер изменения /св при А > 0 показан на рис. 8.10.
|
За интервал времени / = т = 1/а функция Ae~pt уменьшится в е = 2,72 раза. Действитель- но, при г = т = 1/о at - а т = а!а = 1; е“°'= = е"/’х = еч = 1/е = I / 2,72.
Величину т = 1 /а = 1 /\р\ называют постоянной времени цепи; т зависит от вида и параметров схемы. Для цепи на рис. 8.2 т = L / 7?, для цепи на рис. 8.3 т = ЛС, для цепи на рис. 8.18 с - (7?i С) /(/?]+ 7?3) и т. д.
Название «постоянная времени» отражает постоянство подкасательной к экспоненте: подкасательная к экспоненте е-|/т численно равна т (см. рис. 8.10).
§ 8.19 Характер свободного процесса при двух действительных неравных корнях. Пусть р} = -а, р2 = -Ь (для определенности положим b > а). Тогда
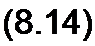 /св = 4 ер‘' + Л2 еР:' = Al e~at + А2 e~bl.
/св = 4 ер‘' + Л2 еР:' = Al e~at + А2 e~bl.
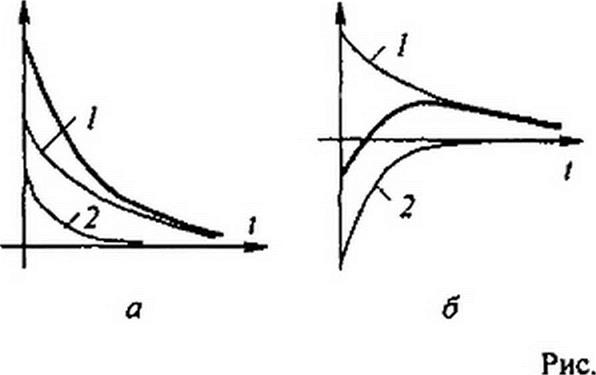
Характер изменения свободного тока при различных по значению и знаку постоянных интегрирования А{ и А2 качественно иллюстрируется кривыми на рис. 8.11, а-г; кривая 1 представляет собой функцию А} e~°’, кривая 2 — функцию А-, е~Ь(; результирующая («жирная») кривая получена путем суммирования ординат кривых 1 и 2.
 | |||
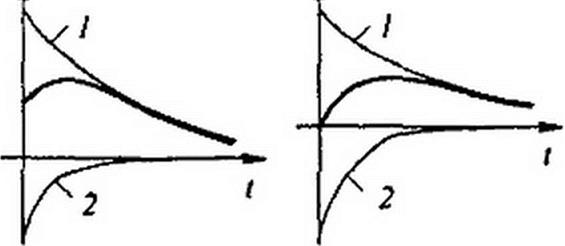 | |||
| ||
|
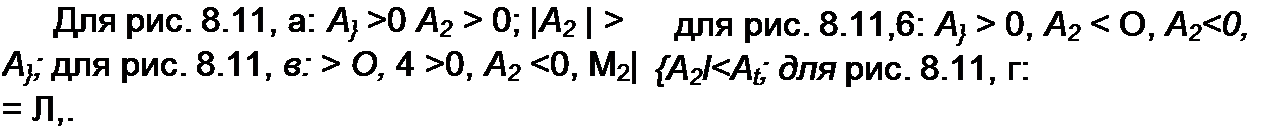 |
§ 8.20  Характер свободного процесса при двух равных корнях. Известно, что если среди корней характеристического уравнения есть два равных корня Ру-р2- ~а> то соответствующие слагаемые решения должны быть взяты в виде
Характер свободного процесса при двух равных корнях. Известно, что если среди корней характеристического уравнения есть два равных корня Ру-р2- ~а> то соответствующие слагаемые решения должны быть взяты в виде
Л, е1” + А2 1 ept =(Л, +А21) е'".
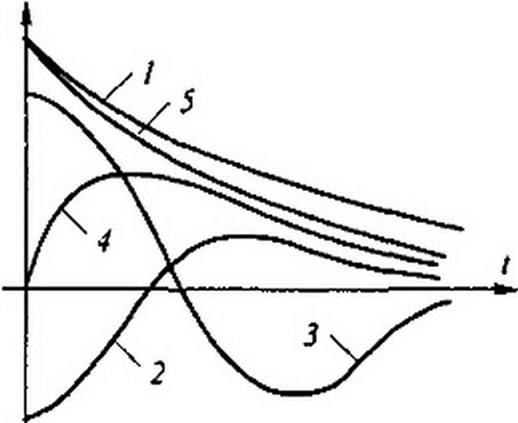
На рис. 8.12 построены пять кривых. Они показывают возможный характер изменения функции (Л, + А2 t)e~ar при различных значениях постоянных интегрирования А{ и Л2, а также при равенстве нулю одной из постоянных.
Кривая 1 построена при А} > 0 и А2 > 0; кривая 2 — при А} < 0 и А2 >0; кривая 3 — при Ах >0 и А2 <0; кривая 4 — при Л] =0 и Л2 > 0; кривая 5 — при Л1 > 0 и Л2 = 0.
 |
|
 |
| ||||
| ||||
§ 8.21 Характер свободного процесса при двух комплексно-сопряженных корнях. Комплексные корни всегда встречаются попарно-сопряженными. Так, если р} = -5 + j <оо, то р2 - -8~j со0. Соответствующее им слагаемое решения должно быть взято в виде
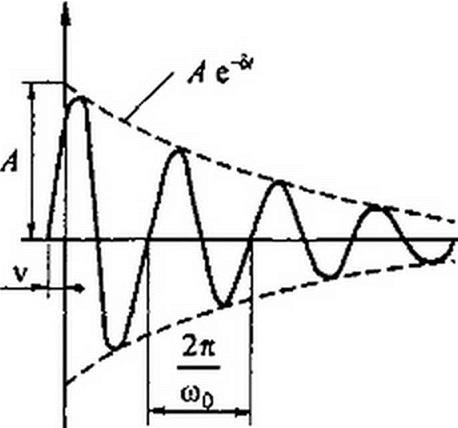
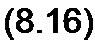 /св = A e’6f sin(co0 / + v).
/св = A e’6f sin(co0 / + v).
Формула (8.16) описывает затухающее синусоидальное колебание (рис. 8.13) при угловой частоте <оо и начальной фазе v. Огибающая колебания описывается кривой Ле"5/. Чем больше S, тем быстрее затухает колебательный процесс; А и v определяются значениями параметров схемы, начальными условиями и ЭДС источника; о)0 и 5 зависят только от параметров цепи после коммутации; со0 называют угловой частотой свободных колебаний; S — коэффициентом затухания.
§ 8.22 Некоторые особенности переходных процессов. Как известно из предыдущего, полное значение любой величины (тока, напряжения, заряда) равно сумме принужденной и свободной составляющих. Если
среди корней характеристического уравнения есть комплексно-сопряженные корни pit2 = -5± у а)0 и значение угловой частоты свободных колебаний о0 почти равно угловой частоте со источника синусоидальной ЭДС (источника питания), а коэффициент затухания S мал (цепь с малыми потерями), то сложение принужденной и свободной составляющих дает колебание, для которого характерно биение амплитуды (рис. 8.14, а).
 |
|
Колебание (см. рис. 8.14, а) отличается от колебаний, рассмотренных в § 7.14, тем, что здесь у одной из составляющих колебания амплитуда медленно уменьшается.
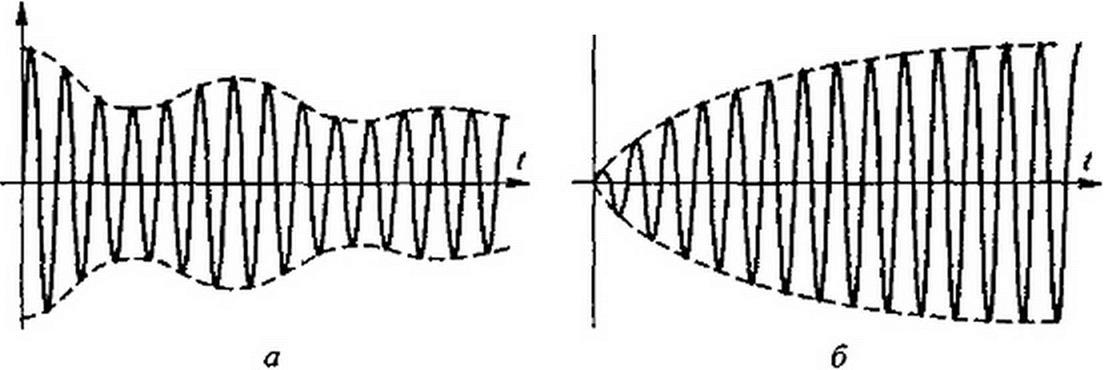
Если угловая частота свободных колебаний <о0 точно равна угловой частоте источника синусоидальной ЭДС, то результирующее колебание имеет форму, изображенную на рис. 8.14, б.
Простейшим примером колебаний такого типа является колебание, возникающее на конденсаторе схемы (рис. 8.15) в результате сложения принужденного cosu>/ и свободного— UCm е cosco t колебаний: Uc - U( т 0 - е’61) COS СО /.
 |
|
 |
|
Амплитуда результирующего колебания нарастает по экспоненциальному закону.
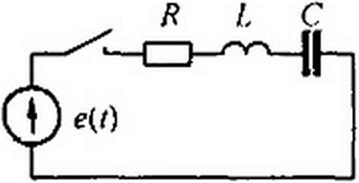
При наличии конденсатора (конденсаторов) в схеме могут возникать большие начальные броски токов, в несколько раз превышающие амплитуды тока установившегося режима. Так, в схеме на рис. 8.16 при нулевых начальных условиях в первый момент после замыкания ключа напряжения на конденсаторах равны нулю и ток в неразветвленной части цепи равен Um sinцу//?,. Если = 90°, то в первый момент после замыкания ключа ток равен Um! Я,. При размыкании ключа в индуктивных цепях возникают опасные увеличения напряжения на отдельных участках (см. § 8.24).
§ 8.23 Переходные процессы, сопровождающиеся электрической искрой (дугой). Если переходный процесс вызывается размыканием ключа в электрической цепи, содержащей индуктивные катушки, то между его расходящимися контактами при определенных условиях может возникнуть электрическая искра (дуга). При этом расчет переходного процесса усложняется и, строго говоря, не может проводиться методами, изучаемыми в данной главе. Объясняется это тем, что сопротивление электрической искры является нелинейной функцией протекающего через нее тока. В этом случае, если известна ВАХ дуги, для расчета переходных процессов могут применяться методы, излагаемые в гл. 16.
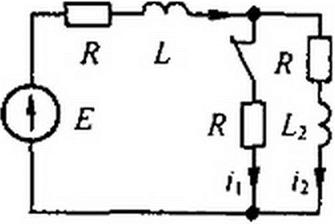
Попытаемся выяснить, можно ли ожидать возникновения электрической искры при размыкании ключа в схеме на рис. 8.17.
До размыкания ключа в цепи был установившийся режим:
/(0_) =------------------ ---
R + 0,5 R 3R
Допустим, что при размыкании ключа искра не возникает. При этом ток /| почти мгновенно уменьшается до нуля, а /(0+) должен равняться /2{0+). Но каждый из токов (q и /2) по первому закону коммутации не может измениться скачком. Следовательно, между достаточно медленно расходящимися контактами ключа при определенных условиях можно ожидать возникновения электрической искры. Расчет переходного процесса в схеме на рис. 8.17 дан в § 8.28.
§ 8.24 Опасные перенапряжения, вызываемые размыканием ветвей в цепях, содержащих индуктивные катушки. При размыкании ключей в электрических цепях, содержащих катушки с большой индуктивностью, на отдельных участках могут возникать напряжения, во много раз превышающие установившиеся. Напряжения, превышающие установившиеся, называют перенапряжениями. Они могут оказаться настолько значительными, что при определенных условиях вызовут пробой изоляции и выход из строя измерительной аппаратуры.
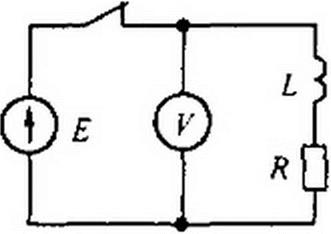
Пример 79. К зажимам индуктивной катушки с /? = 1000м; £ = 10 Гн; подключен вольтметр (рис. 8.18). Сопротивление вольтметра R>- = 3000 Ом; £ = 100 В. Найти приближенное значение напряжения на зажимах вольтметра при / = 0+. если допустить, что размыкание ключа произойдет мгновенно и искры не возникнет.
Ре ш е н и е. До размыкания ключа через £ протекает ток / = Е / R ~ 1 А. В индуктивной катушке была запасена магнитная энергия £/2/2. Если допустить, что размыкание ключа произошло мгновенно и искры не появилось, и учесть, что ток через £ должен оставаться равным 1 А, то по замкнутому контуру, составленному вольтметром и катушкой, за счет запаса энергии магнитного поля индуктивной катушки в первое мгновение будет протекать ток в 1 А. При этом на вольтметре возникнет пик напряжения 2 кВ. Прохождение большого импульса тока через вольтметр может вызвать перегорание катушки прибора и выход его из строя.
 |
| ||||
| ||||
 |
|
При размыкании ключа с конечной скоростью между его расходящимися контактами возникнет электрическая искра. Это приведет к тому, что увеличение напряжения на вольтметре будет меньше, чем в только что рассмотренном идеализированном случае, когда ключ размыкался мгновенно без искры.
При более детальном рассмотрении процесса необходимо еще учесть влияние межвитковых емкостей и емкостей на землю (см. § П.1). Если не учитывать возникновение искры, распределенные емкости и индуктивности, то приведенный расчет является грубым и носит иллюстрированный характер.
Чтобы не «сжечь» вольтметр в цепи (см. рис. 8Л 8), сначала следует отключить вольтметр, а затем разомкнуть ключ. Перенапряжения проявляются тем сильнее, чем больше индуктивность в цепях. Особенно опасны они в цепях постоянного тока, содержащих индуктивности порядка единиц и десятков генри. В таких цепях при отключениях соблюдают специальные меры предосторожности (ключ размыкают после введения дополнительных резисторов в цепь).
§ 8.25 Общая характеристика методов анализа переходных процессов в линейных электрических цепях. Расчет переходных процессов в любой линейной электрической цепи состоит из следующих основных операций:
1) выбора положительных направлений токов в ветвях цепи;
2) определения значений токов и напряжений непосредственно до коммутации;
3) составления характеристического уравнения и нахождения его корней;
4) получения выражения для искомых токов и напряжений как функции времени.
Широко распространенными методами расчета переходных процессов являются:
1) метод, называемый в литературе классическим;
2) операторный метод;
3) метод расчета с помощью интеграла Дюамеля.
Для всех этих методов перечисленные операции (этапы расчета) являются обязательными. Для всех методов первые три операции совершают одинаково, и их необходимо рассматривать как общую для всех методов часть расчета. Различие между методами имеет место на четвертом, наиболее трудоемком этапе расчета.
Чаще используют классический и операторный методы, реже — метод расчета с применением интеграла Дюамеля. В дальнейшем будут даны сравнительная оценка и рекомендуемая область применения каждого из них (см. § 8.56).
В радиотехнике, вычислительной и импульсной технике, электронике, автоматике и в технике, связанной с теорией информации, кроме этих трех методов применяют метод анализа переходных процессов, основывающийся на интеграле Фурье. (Об интеграле Фурье и спектральном методе, основывающемся на интеграле Фурье, см. гл. 9.) Для исследования характера переходного процесса, описываемого уравнениями высоких порядков, используют моделирующие установки, а также метод пространства состояний (см. § 8.66).
§ 8.26 Определение классического метода расчета переходных процессов. Югассическим методом расчета переходных процессов называют метод, в котором решение дифференциального уравнения представляет собой сумму принужденной и свободной составляющих. Определение постоянных интегрирования, входящих в выражение для свободного тока (напряжения), производят путем совместного решения системы линейных алгебраических уравнений по известным значениям корней характеристического уравнения, а также по известным значениям свободной составляющей тока (напряжения) и ее производных, взятых при / = 0+.
§ 8.27 Определение постоянных интегрирования в классическом методе. Как известно из предыдущего, любой свободный ток (напряжение) можно представить в виде суммы экспоненциальных слагаемых. Число членов суммы равно числу корней характеристического уравнения.
При двух действительных неравных корнях
4в ~ 4 еА' + Л еРг/;
при трех действительных неравных корнях
/св = 4, е/,|/ + А2 еР1' +А3 tPi'.
Для любой схемы с помощью уравнений Кирхгофа и законов коммутации можно найти: 1) числовое значение искомого свободного тока при / = 0+, обозначим его /св(0+);2) числовое значение первой, а если понадобится, то и высших производных от свободного тока, взятых при t = 0+. Числовое значение первой производной от свободного тока при / = 0+ обозначим /'в(0+); второй— /*в(0+) и т. д.
Рассмотрим методику определения постоянных интегрирования AhA2,,..t полагая известными /св(0+), £в(0Д У'в(0+) и значения корней рнр2,....
Если характеристическое уравнение цепи представляет собой уравнение первой степени, то /с0 = A ер'. Постоянную интегрирования А определяют по значению свободного тока /„(0.): СВ > < Z
Л = /св(0+). (8.17)
Если дано характеристическое уравнение второй степени и его корни действительны и не равны, то
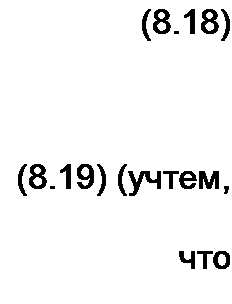 'св = 4 e/v + Л еР:'.
'св = 4 e/v + Л еР:'.
Продифференцируем это уравнение по времени:
'св = Р1 4 ер,'+Рз Я2е^7.
Запишем уравнения (8.18) и (8.19) при / = 0 е*' = ePi' =1 при t = 0).
В результате получим:
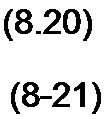 4,(0.)= Л,+Л2;
4,(0.)= Л,+Л2;
Zce(<M - Р] А) + Pl А2‘
В этой системе уравнений известными являются /св(0+), /сВ(0+), р, и р2; неизвестными — Ах и Аг.
Совместное решение (8.20) и (8.21) дает
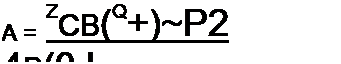 | |||||||
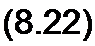 | |||||||
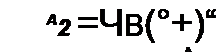 | |||||||
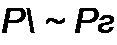 | |||||||
Если корни характеристического уравнения являются комплексно-сопряженными, то в (8.18) сопряжены не только р} и р2 (А, 2 = -5± J со0), но и А{ и А2. Поэтому свободный ток
 | |||
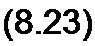 | |||
Угловая частота со0 и коэффициент затухания 5 известны из решения характеристического уравнения.
Определение двух неизвестных А и v производят и в этом случае по значениям /св(0+)и /’сВ(0+).
Продифференцировав по времени уравнение (8.23), получим
= ~А & е"*' sin(co0 t + v) + A w0 е'5' cos(<o0 t + v). (8.24)
Запишем уравнение (8.24) при / -0+ :
!св ($♦ ) = -Л S sin v + Л о)о cos v.
Таким образом, для нахождения неизвестных А и v имеем два уравнения:
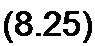 4в(°+) = А $in v;
4в(°+) = А $in v;
<в(0+) = ~А § sin v + А со0 cos v.
Для цепи, имеющей характеристическое уравнение третьей степени, свободный ток
 ZCB - Л, еА' + А2 е^Ме'”'.
ZCB - Л, еА' + А2 е^Ме'”'.
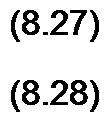 Найдем первую, а затем вторую производную от левой и правой частей уравнения (8.26):
Найдем первую, а затем вторую производную от левой и правой частей уравнения (8.26):
С = А Л ePl' +Р2А2 еРг' +РзАз еРу‘‘>
Се = Р. А\ еР'' + Р2 А2 ePi' + Pl аз еР''
Запишем (8.26)-(8.28) при t = 0+:
4л(®+) ~ Л + ^2 + Л»
 С(°+) = Р\ Л\+Р2 А2+ру А3\
С(°+) = Р\ Л\+Р2 А2+ру А3\
ice ~ р\ + Р1 А2 + Рз А3.
Система уравнений (8.29) представляет собой систему трех линейных алгебраических уравнений с тремя неизвестными: А}> Л2 и А3. Все остальные входящие в нее величины (р}, р2 р3, /св(0+), /сВ(0+), *св(0+)) известны.
Сначала, пока еще не накоплено опыта в решении задач, для облегчения расчета величины и ее производной (производных) при t = 0+ рекомендуется решать задачу относительно тока через L или напряжения на С и только затем, используя законы Кирхгофа, определять любую другую величину через найденную.
Рассмотрим несколько примеров расчета переходных процессов классическим методом в цепях первого и второго порядков с источниками постоянной и синусоидальной ЭДС при ненулевых начальных условиях.
Пример 80. В схеме на рис. 8.19 до замыкания ключа был установившийся режим: Л) = = /?3 = 50 Ом; С - 100 мкФ; Е - 150 В. Требуется найти: 1) полные, принужден
ные и свободные составляющие токов /]. iz, i3 и при / = 0„, а также начальное значение производной от свободного напряжения на конденсаторе; 2) токи /2, iy и напряжение ис в функции времени.
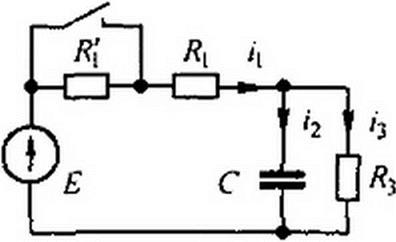
|
Решение первой части задачи. До коммутации /2(0 ) = 0 и i|(0.) =и3(0_) = £/(Л,+/?; +R3)= 150/150 = 1 А.
Напряжение на конденсаторе равно напряжению на резисторе R3: а((0_) = /3(0_) R3 = I -50 = 50 В.
Найдем принужденные значения токов и напряжений после коммугацнн:
Е 150 КА
= = юо= 1,5 '
Кз = 1-5'50 = 75В.
По второму закону Кирхгофа составим уравнение для контура, образованного первой и второй ветвями при г = 0+ :
>1(0,) /?] + «г(0+) = £. но «с(0+)= «с(О-).
Поэтому
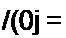
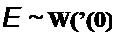 150-50 . А
150-50 . А
----------- = 2 А.
50
Из уравнения ) = i3(0^) R3 получим
/3(0,) = i/(-(0,)//?3 = I А.
По первому закону Кирхгофа q(0+) = ь(0+) + /3(0*). Следовательно,
A(OJ = ;1(OJ-/3(OJ = 2-1 = 1 А.
|
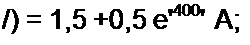 Свободные составляющие тока и напряжения при I = 0+ определим ках разности между полными и принужденными величинами:
Свободные составляющие тока и напряжения при I = 0+ определим ках разности между полными и принужденными величинами:
«Сс.(0♦) = «с(04) - «спР(0+) = 50- 75 = -25 В;
/|СВ(0+) = г,(0+) - /,пр(0+) = 2 -1,5 = 0,5 А;
(0 J (О J - /2пр (0 J = I - 0 = 1 А;
'Зсв(О>) = 'з(О^)-Ъпр(°-) = 1-1,5 = -0,5 А.
Так хак свободный ток через конденсатор
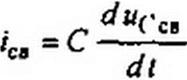 | |||
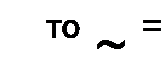 | |||
В рассматриваемом примере
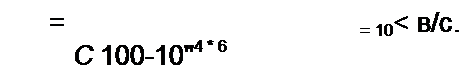 |
Решение второй части задачи. Характеристическое уравнение для послекоммутационной схемы р Ry /?3 С + + /?з = 0 имеет один корень
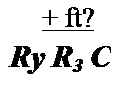 | |||
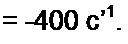 | |||
Каждый ток равен сумме принужденной и свободной стпаапяощей а с1". где А равно значению свободной составляющей при i - 0, (рис. 8.20):
/2=е“400/А; G = 1.5-0.5 е"100'; ис = 75- 25 е"400' В.
Пример 81. В схеме (рис. 8.21) до замыкания ключа был установившийся режим: /?1 = R2 = 2 Ом; со£ = 30м; e(i) = 127 sin(a) t - 50°) В; о = 314 рад/с. Требуется определить: 1) /с>(0+); 2) закон изменения тока в цепи после коммутации.
Решение первой части задачи. Комплексная амплитуда тока в цели до коммутации
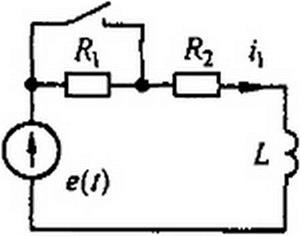 |
|
 |
|
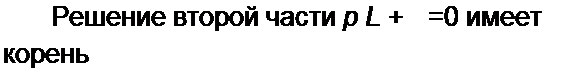 | |||||
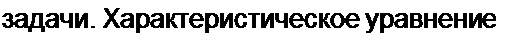 | |||||
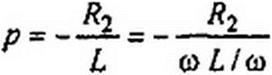 | |||||
|
 |
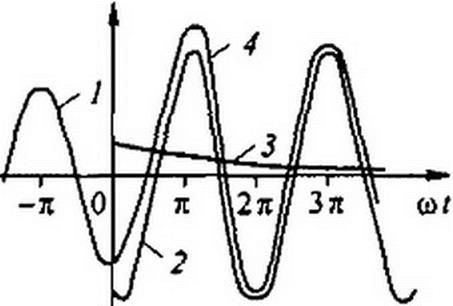
По данным первой части задачи ток в цепи до коммутации (кривая / на рис. 8.22 до <о t = 0)
i = 25.4 sin(o) t - 86’50') A.
Мгновенное значение принужденного тока после коммутации (кривая 2 на рис. 8.22)
/пр = 35,2 sin(o) t -106’20') A; ict(0¥ ) = 8,45 А.
Следовательно,
i = гпр + /св - 35,2 sin(ci) t -106’20') + 8,45 е"2)0' А.
Кривая 3 на рис. 8.22 определяет характер изменения свободного тока, кривая 4 — полного тока после коммутации (ординаты кривой 4 при w/^О равны сумме ординат кривых 2 и 3).
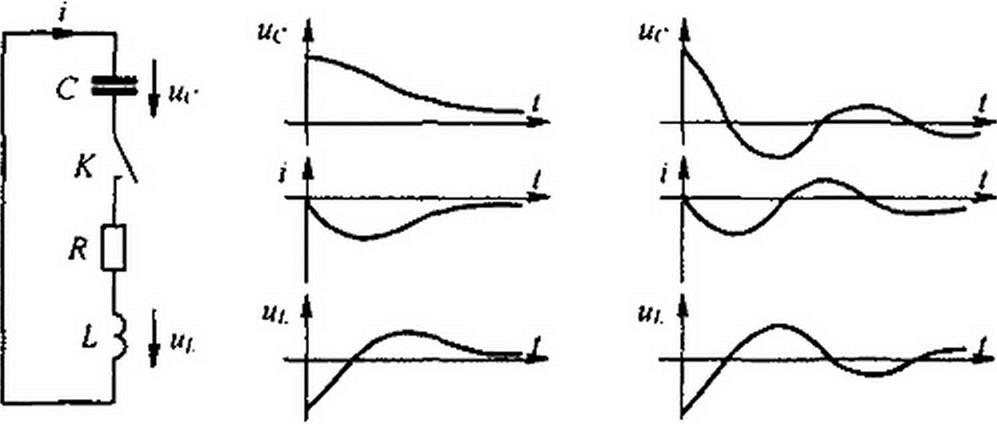
Пример 82. Конденсатор емкостью С. заряженный до напряжения wr(0), при замы
кании ключа К разряжается на £ и А (рис. 8.23, а). Вывести
ки изменения во времени «<>, /. у/, когда корни характеристического уравнения: а) действительные; б) комплексно-сопряженные.
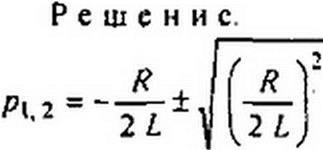 |
|
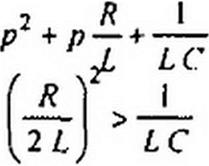 |
|
 |
| ||||
| ||||
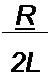 | |||||
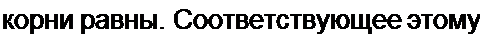 | |||||
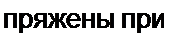 | |||||
случаю R называют критическим. При решении учтем, что /(0) = 0, 'Пр = О, "спр = а) Полагаем з — действительные корни. Тогда
«Сев = 4 с*' + А2 cPit‘.
<Сс, • С -- р, А, сР|' +р2 Л2 at
Составим два уравнения для определения А} и Л2:
Л| + ^2 ~ «с (0k Pi + Pz ^2 ~ 0.
Отсюда
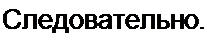 |
л _ «с (0) Рг . Л) _ «с (°) Р\
Рг~ Р\ ' Pi ~ Pi
a(. = -M2L(p2e,V-P1e«-);
Pi- Pl
i = CPi A}
u,_ = LC pi Ai (pi cl>l 1 -p2 e,,J').
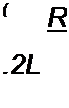
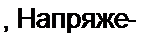 Графики uc, i, ut для случая а) даны на рис. 8.23, б.
Графики uc, i, ut для случая а) даны на рис. 8.23, б.
Для случая б) корни р, 2 = -5±/ о0. где § = R/2 L; ы0 = ние иСсл = А е 61 sin(a>0 / + v).
Ток
(-6 sin(o0 / + v) + c)0 cos(<BO < + v)) - ACe 6f sin(COo / + v + 0).
Здесь tg3 = <оо / (-S), угол 0 находится во второй четверти. Из начальных условий
w(-(0) - A sin v и /св(0) -AC sin(v + 0) = 0.
Отсюда
tgV (Ол
v+ 0 = 180°; jgv = o>0/5; sin v =-j====-=-у===-.
yl + fg*’V •уб^+Wo
Постоянная
Л = = ис(0) 71 + (8/<о0)2
sin v
Графики
и(- = A e-Szsin(o0 t + v); i = -A C ^82 +coq e"5' sino0 i = -A jc!L c~6/sino)0 r;
и, - (З2 +Шл) ACL e-5/ sin(o0 t - v) = e~8/ sin(w0 t- v)
sin v
изображены на рис. 8.23, e; и/,(0+) =-wc(0).
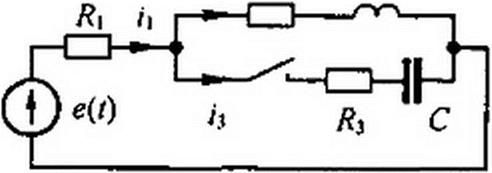
Пример 83. В схеме (рис. 8.24) ключ замыкается в третьей ветви. До этого был установившийся режим. е(/) = £ = 120В. Требуется найти: 1) ^C8(0tX >
«г'св(°+). (^«Ссв z^)o. ’• 2) i2(t), если R{ 50 Ом. R2 = 10 Ом, L, = 2 Гн, /?3 = 50 Ом, С - 150 мкФ.
 |
| ||||
| ||||
 |
|
Решение первой части задачи. До замыкания ключа
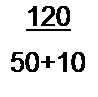 | |||||
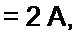 | |||||
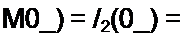 | |||||
Принужденный ток после коммутации /)пр = /2пр = 2 Л. Постоянный ток через конденсатор не проходит, поэтому /Зпр = 0.
От постоянного тока на индуктивном элементе нет падения напряжения, следовательно, «Л2пр=°-
Принужденное напряжение на конденсаторе равно падению напряжения на /?2 оттока ьПр: г/г = 210 = 20 В, По первому закону коммутации г2(0_) =/2(0+) = 2 А. Но 6(0j = /2np(0+) + /2ce(0+), откуда
/2„(0 ♦ ) = й(0 J-/2np(0J = 2-2 = 0;
/I(OJ = /2(OJ+/3(OJ.
или
/,(OJ = 2 + /3(OJ.
Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного первой и третьей ветвями:
/1(0+)Л1+М0>)Л3+^(О.) = £.
Так как и( (0+) = 0 и /((0+) = 2 + z3(0+). то
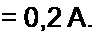 . ,Л ч £ - 2 /?| 120-2-50
. ,Л ч £ - 2 /?| 120-2-50
'з 0+ ) =------------ - =-------------
/?, + Ry 50+50
Свободная составляющая
WO J = Ъ(0+) - ,3np(0 J = 0.2 - 0 = 0,2 А.
Чтобы определить ц/.св(0>) составим уравнение для свободных составляющих по контуру, образованному первой и второй ветвями:
Лсв(0+ ) £| + *2св(0+ ) ^2 + w /.c#(0+ ) - 0.
откуда
"z,C8(0+) = -6«(0+) - '2св(0>) Я2 = -0.2 50 - 0 = -10 В.
Но u(ct = L2 . Следовательно, си
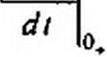 |
|
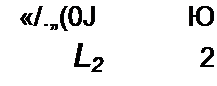 | |||
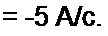 | |||
Свободное напряжение на конденсаторе при г 0+ подсчитаем по второму закону коммутации:
ис(0_)= ur(0+ )1 wr(0+) = uCn}>(0+) + uCcjO+); 0 = 20 + иСсв(0ф), отсюда «гс.(0+) = -20 В.
Определим скорость изменения свободной составляющей напряжения на конденсаторе при {a 0t. С этой целью воспользуемся тем, что /Зсв = С du '-c*. Следовательно, dt
^£1. = = —9^— = 1333В/с.
dt С 150Ю'6
Решение второй части з а д а ч и. Характеристическое уравнение
L2 С (Л| + Л2) + р (С (/?2 Д} + Д| ^2 + ^1 /?з) + ^2 ) + + Д2 = Q
имеет два комплексно-сопряженных корня:
Pi = -42,1 + j 15,2 с"1,
рг =-42.1- j15,2с"’.
Поэтому свободная составляющая должна быть взята в виде
А е"6' sin(coo / + V).
где 8 = 42,1; = 15.2; Ли v определяем по значению свободной составляющей и ее пер
вой производной при / = 0*. По данным первой части задачи, t2 =2 А; ьсв(0+) = 0; /2се(0+) = -5А/с; «Гпр = 20В; wrce(0j-20 В; и'(Чъ(0J = 1333 В/с.
При / = 0 Ле‘6' sin(o0 t + v) = A sinv. Производная функция Л е"6'sin(coo r +v):
- Л 8 е'6' $in(t>0 / + v) + А е "5' о0 cos(<d0 t + v).
Значение этой производной при / = 0 равно -8 Л sin v + <о0 A cos v.
Найдем значения Л и v для свободной составляющей тока i2. Для этого составим два уравнения:
/2с«(0*)в0 или Xsinv = 0;
/2св(0+) = -5 или -8 Л sin v + cj0 Л cos v =-5.
Совместное решение их дает А = -0,328 А и v = 0. Следовательно,
'2 = '2пр + '2с. = 2 - W28 е’42,1' 15,2 t А.
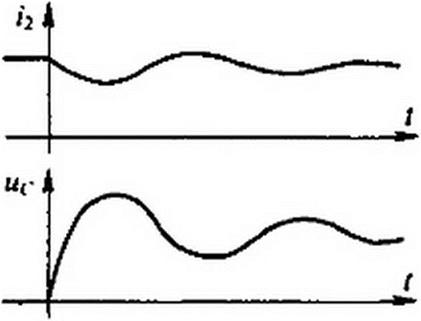
Кривая / на рис. 8.25 выражает собой график /2 = f(t). Найдем Л и v для свободной составляющей напряжения и(-:
ыСсв(0.,) =-20 или Л sin v = -20;
MCc»(0+)=i= l^33 или -8 A sin v +coo A cos v = 1333.
Отсюда A = 37,9; v = 31°52'.
Таким образом, u (' ~uCnp +u(c» - 20+37,9 e"421' sin 15,2/ A.
Кривая 2 на рис. 8.25 изображает ис = f{t).
Пример 84. В схеме на рис. 8.24 е(/) = 127 srn(314 г+ 40°) В. Параметры схемы те же, что и в примере 83. До замыкания ключа в схеме был установившийся режим.
Требуется найти: I) /2св(0+); ; uCc,(0J; -~с‘ : 2) i(t), uc(t}.
d ‘ о. d{ o+
Решение первой части з а д а ч и. До коммутации
= / = *27е72° ■■ = 0,202 е"7 44’30'
2т 60+у 628
/| = i2 = 0.202 sin(o t - 44’30');
6(0.) = /2(0.) = 0,202 sin(-44°30') = -ОД 4 J 5 А.
Определим принужденные токи и напряжения на конденсаторе после коммутации. Входное сопротивление цепи
( J
(Л2+У<лТ2) /?3--------- —
ZBX = Л, +---------------------- = 104.8 е’79‘50’ Ом.
Л2 + / со Д2 + /?з---- —
й> С
Тогда /)яг = Ё|Ж/Zex = 127 е740’/104,8 е'7 9050 = 1,213 е749*50.
Мгновенное значение принужденного тока после коммутации
6пр = 1.213 sin(co/ +49’50’);
6 лр (04) = 1.213 sin(49’50 ’) = 0.923 А.
Комплексное сопротивление параллельно соединенных второй и третьей ветвей
(R2+J(aL2) /?3 -
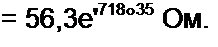 к
к
23 -
R2 + J
Комплексное напряжение на параллельном участке
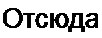 и27„ = 1]п> Z2J = 1.213е/49°50 56.3 е'718“35’= 68,2 е'310’5' 0.
и27„ = 1]п> Z2J = 1.213е/49°50 56.3 е'718“35’= 68,2 е'310’5' 0.
/ = s 68>2е,._П 15 я 0,1085 е 7 58’4$‘
2w Z2 10 + 7628
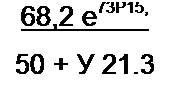 | |||
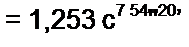 | |||
Мгновенные значения принужденных токов i2 и /3 после коммутации:
/2пр = 0,1085 sin(co/-58’45');
/Зпр = 1,253 sin(o I + 54’20');
'2пр (° J = 0,1085 sin(-58°45’) = -0,0928 А;
/3пр(0+) = 1.253 sin 54’20' = 1,016 А.
Принужденное напряжение на конденсаторе
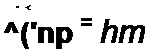 1,253e7 54’20■21.3e-790O=26.7e-73^O4<,' В.
1,253e7 54’20■21.3e-790O=26.7e-73^O4<,' В.
Мгновенное значение принужденного напряжения на конденсаторе после коммутации иСпр = 26,7 sin(<o t - 35°40'); нСпр(0+) = 26,7 sin(-35°40') = -15,57 В.
По первому закону коммутации,
'з(0-) = ) = -0,1415 = /2пр(0+) + /2св(0+);
/2пр (0+) - 0,0928 А; /2с,(0+) = -0,1415 + 0,0928 = -0,0487 А.
Свободное напряжение на конденсаторе «сС8(0+) найдем по второму закону коммутации:
иС (0.) = нГпр(0+) + мГсв(О+);
«Сс8<0+)=ЦГ(0_)-ЫГпр(04) = 0-(-15,57) = 15,57 В.
Для определения /зсв(0+) составим уравнение по контуру, образованному первой и третьей ветвями:
6с.(Of) Я| +Iic»(0f) R3 +«c»(0J = 0.
Заменим в нем /1св(0+) на (-0,0487 + /Лсв(0+)), и. учтя, что ^Ссв(0+) = 15,57 В, получим
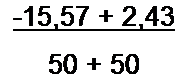 | |||
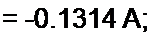 | |||
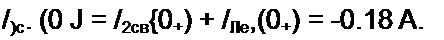 | ||||||
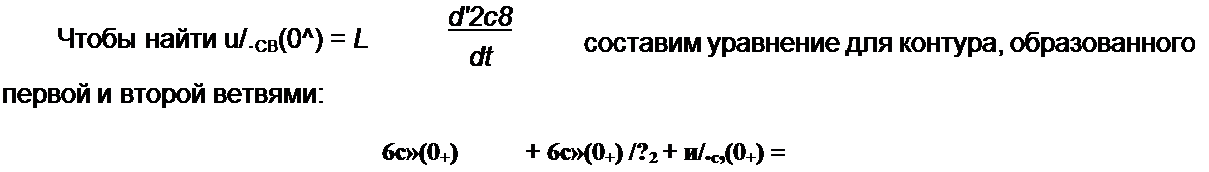 | ||||||
 | ||||||
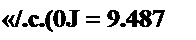 | ||||||
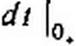 |
|
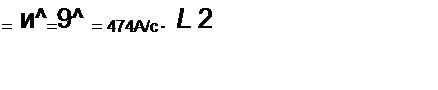 | |||||||
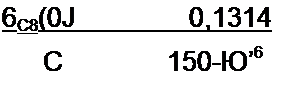 | |||||||
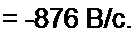 | |||||||
 | |||||||
Решение второй части задачи. По данным, полученным при решении первой части,
/2пр = 0.1085 sin(w t - 58°45'), /2св(0, } = -0,0487 А;
'2c,(0j = 4,74 А/с;
иГпр = 26.7 sin(o/-35°40'), мГсв(0,.) = 15,57 В;
^■с.(0+)=“876В/с;
Корни характеристического уравнения те же, что и в предыдущем примере. Определим А и v для i2ca, составим два уравнения:
A sin v = -0.0487; 6 A sin v + <оо A cos v = 4,74.
откуда А = 0,184 A; v = -15°20'.
Следовательно,
i2 = ,2ffp + /2св = 0,1085 sin(co t - 58°45') + 0,184 c’42J' sin(l 5,21 -15’20') A.
Найдем А и v для wCci, составим два уравнения:
A sin v - 15,57; -5 A sin v + coo A cos v = -876.
Их совместное решение дает А = 213; v = 136°50'.
Таким образом,
ис = «с'пр + иСсв = 26,7 sin(© / - 35°40’) + 21,3 е'42л' sin(l5,2 / +136°50') В.
§ 8.28. О переходных процессах, при макроскопическом рассмотрении которых не выполняются законы коммутации’*. Обобщенные законы коммутации. На практике встречаются схемы, переходные процессы в которых состоят как бы из двух стадий резко различной продолжительности, Длительность первой стадии в тысячи и миллионы раз короче второй. В течение первой стадии токи в индуктивных элементах и напряжения на конденсаторах изменяются настолько быстро (почти скачкообразно), что если считать t = 0_ началом, a t = 0+ — окончанием первой стадии, то создается впечатление, что при переходе от t = 0_ к t - 0+, т. е. за время, например, в несколько микросекунд, как бы нарушаются законы коммутации.
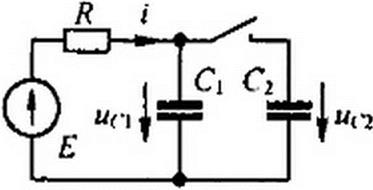
Для иллюстрации нарушения второго закона коммутации рассмотрим переходный процесс в схеме (рис. 8.26) с начальными условиями иС1(0_) = Е, иС2(0_) = 0.
Сначала при замыкании ключа через конден
|
саторы возникают очень большие броски токов (ограничиваемые хотя и очень малыми, но все же конечными сопротивлениями соединительных проводов Япр), прохождение которых приводит почти к мгновенному уравниванию напряжения на конденсаторах до значения, меньшего Е. (Строго говоря, если учесть сопротивление /?пр, то для первой стадии переходного про
цесса в схеме на рис. 8.26 характеристическое уравнение будет уравнением второго порядка, один корень которого при /?пр -» 0 стремится к бесконечности.)
После этого начинается вторая стадия, когда параллельно соединенные конденсаторы относительно медленно заряжаются до напряжения £. Длительность переходного процесса практически определяется второй стадией.
В качестве примера нарушения первого закона коммутации рассмотрим переходный процесс в схеме на рис. 8.17. Быстрое размыкание ключа в первой ветви, например за 10“5 с, приводит к тому, что сопротивление этой ветви быстро увеличивается, ток Z, почти скачком уменьшается до нуля и почти скачком изменяются токи в остальных ветвях.
"’Имеются в виду ранее рассмотренные законы коммутации.
Таким образом, за очень малое время порядка ] О-5 с (от / = 0_ до t = 0+) токи резко изменяются, a i(0+) * /(0_); ^(О^.) * /2(0_).
Нарушение законов коммутации в формулировке § 8.5, 8.6 при переходе от t - 0_ до / - 0+ объясняется тем, что процессы в быстро протекающей первой стадии и их зависимость от времени не рассматриваются. Если же первую стадию не исключать при рассмотрении, то ранее исследуемые законы коммутации выполняются.
Для того чтобы можно было рассчитать переходные процессы сразу во второй стадии, как бы перешагнув через первую, надо, во-первых, примириться с тем, что при переходе от t = 0_ до t - 0+ в рассматриваемых задачах законы коммутации в том виде, как они сформулированы в § 8.5, 8.6, не будут выполнены; во-вторых, принять исходные положения, которые позволяют определить значения токов через индуктивности и напряжений на конденсаторах (а если потребуется, то и их производные) при t - 0+ через значения токов и напряжений при t = 0. Таких положений (правил) два. При решении задач рассматриваемого типа они заменяют законы (правила) коммутации, о которых шла речь в § 8.5, 8.6, и потому их называют иногда обобщенными законами (правилами) коммутации.
§ 1.1 переходе от t = 0_ до / = 0+ суммарное потокосцепление каждого замкнутого контура послекоммутационной схемы не должно претерпевать скачкообразных изменений. Это положение следует из второго закона Кирхгофа и доказывается от противного: если допустить, что некоторого контура изменится скачком, то в уравнении для этого контура, составленном по второму закону Кирхгофа, появилось бы слагаемое д£ц//Д/| и второй закон Кирхгофа не был бы выполнен.
Суммарное потокосцепление представляет собой алгебраическую сумму произведений токов ветвей этого контура на индуктивности их индуктивных элементов (в общем случае с учетом магнитной связи с другими ветвями). Со знаком плюс в эту сумму входят слагаемые ветвей, направление токов в которых совпадает с произвольно выбранным направлением обхода контура.
§ 1.2 переходе от / = 0. до t = 0+ суммарный заряд на обкладках конденсаторов, присоединенных к любому узлу послекоммутационной схемы, должен остаться неизменным. Если этого не выполнить, то суммарный ток, проходящий через конденсаторы, был бы бесконечно большим (стремился бы к бесконечности), бесконечно большими были бы токи и через другие ветви, присоединенные к этому узлу. Это также привело бы к нарушению второго закона Кирхгофа.
Пример 85. В схеме рис. 8.17 до размыкания ключа был установившийся режим. Определить ток в цепи после коммутации.
Решение. Послекоммутационная схема (см. рис. 8.17) имеет всего один контур. По первому закону (правилу) коммутации:
Д/(0_)+Д2 /2(0_) = ((0+)(£ + /.,); <(0,)=■■- 1 (£/(0_) + £2 г2(°- »•
Закон изменения тока при zsO+t если считать, что до коммутации был установившийся режим,
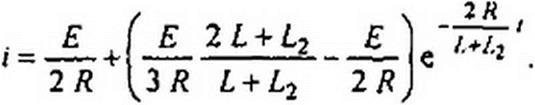 | |||
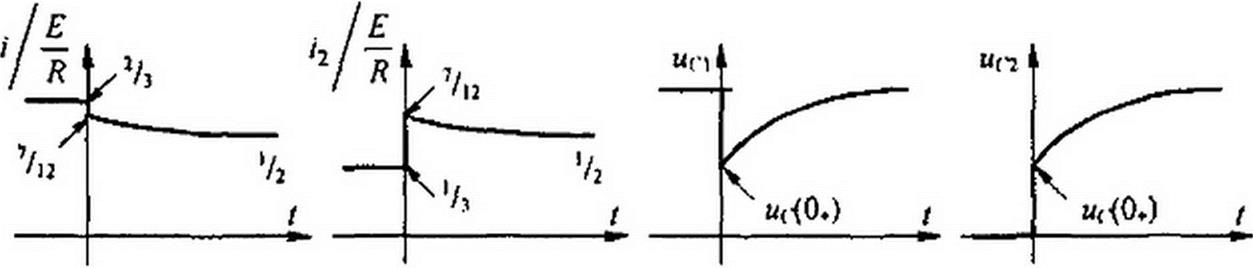 | |||
| ||||
| ||||
Пример 86. Определить закон изменения напряжений uC] и »С2 при замыкании ключа в схеме на рис. 8.26.
Решение. В схеме известны и(->(0_) = £; i/f-2(0+) = 0 По второму закону (правилу) коммутации составляем одно уравнение (т. е. столько, сколько необходимо составить
уравнений для послекоммутационной схемы по первому закону Кирхгофа):
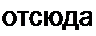 | |||||||||||
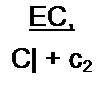 | |||||||||||
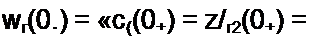 | |||||||||||
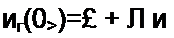 | |||||||||||
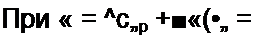 | 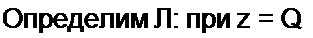 | ||||||||||
«с = Е - £
Ч т I " -
Характер изменения и исг показан на рис. 8.27, в, г.
В заключение обратим внимание на то. что, допустив при переходе от / - 0_ к ( = 0+ скачкообразное изменение токов через индуктивный элемент и скачкообразное изменение напряжений на конденсаторах, тем самым допускаем скачкообразное изменение энергии магнитного поля индуктивных элементов и энергии электрического поля конденсаторов.
Суммарная энергия электрического и магнитного полей при / = 0+ всегда меньше суммарной энергии при t - 0_, так как часть запасенной энергии расходуется на тепловые потери в резисторах, искру при коммутации, электромагнитное излучение в окружающее пространство.
Прежде чем перейти к изучению основ второго метода расчета переходных процессов в линейных электрических цепях — операторного метода, вспомним некоторые известные положения.
§ 8.29 Логарифм как изображение числа. Известно, что для выполнения операций умножения, деления, возведения в степень и извлечения корня из многозначных чисел целесообразно пользоваться логарифмами.
Действительно, операция умножения сводится к сложению логарифмов, операция деления — к вычитанию логарифмов и т. д. Таким образом, произвести расчет легче в силу того, что сравнительно сложная операция сводится к более простой. Каждому числу соответствует свой логарифм, поэтому логарифм можно рассматривать как изображение числа. Так, 0,30103 есть изображение (логарифм) при основании 10 числа 2.
§ 8.30 Комплексные изображения синусоидальных функций. С понятием изображения встречаются также при изучении символического метода расчета цепей синусоидального тока. Согласно символическому методу, комплексная амплитуда есть изображение синусоидальной функции. Так, 1т— изображение синусоидального тока Im sin(<o t + iy). Между изображением числа в виде логарифма и изображением синусоидальной функции времени в виде комплексного числа имеется существенная разница. В первом случае речь идет об изображении числа (не функции), во втором — об изображении функции времени.
Подобно тому как ведение логарифмов упростило проведение операций над числами, введение комплексных изображений синусоидальных
ункций времени позволило упростить операции над функциями времени (свести операции расчета цепей синусоидального тока к операциям, изученным в гл. 2).
§ 8.31 Введение в операторный метод. Операторный метод тоже основан на использовании понятия об изображении функций времени, В операторном методе каждой функции времени соответствует функция новой переменной, обозначаемой буквой р, и наоборот — функции переменной р отвечает определенная функция времени.
Переход от функции времени к функции р осуществляют с помощью преобразования (прямого) Лапласа.
Таким образом, операторный метод расчета переходных процессов представляет собой метод расчета, основанный на преобразовании Лапласа.
Операторный метод позволяет свести операцию дифференцирования -к умножению, а операцию интегрирования — к делению. Это облегчает интегрирование дифференциальных уравнений.
§ 8.32 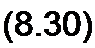 Преобразование Лапласа. Условимся под р понимать комплексное число
Преобразование Лапласа. Условимся под р понимать комплексное число
р = а + jb>
где а — действительная, a jb — мнимая части комплексного числа (в ряде книг вместо буквы р пишут $).
 В дальнейшем в соответствии с установившейся практикой коэ4
В дальнейшем в соответствии с установившейся практикой коэ4
 циент b с учетом знака условимся называть не коэ<{ мой части комплекса (чем он в действительности является), а мнимой частью. Функцию времени (ток, напряжение, ЭДС, заряд) обозначают
циент b с учетом знака условимся называть не коэ<{ мой части комплекса (чем он в действительности является), а мнимой частью. Функцию времени (ток, напряжение, ЭДС, заряд) обозначают
f(t) и называют оригиналом. Ей соответствует функция F(p}, называемая изображением, которая определяется следующим образом:
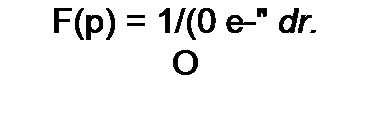 | |||
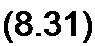 | |||
Соответствие между функциями F(p) и /(/) записывают так:
F(p^f(t). (8.32)
Знак «=» называют знаком соответствия.
Верхний предел интеграла (8.31) равен бесконечности. Интегралы с бесконечным верхним пределом называют несобственными. Если в результате интегрирования и подстановки пределов получают конечное число (не бесконечность), то говорят, что интеграл сходится.
В курсе математики доказывается, что интеграл (8.31), в состав которого входит функция е"р/ = е'а/ е“;Л', сходится только в том случае, когда модуль функции /(/), если и увеличивается с ростом /, то все же медленнее, чем модуль функции ер1, равный е*'.
Практически все функции /(/), с которыми имеют дело в курсе ТОЭ, этому условию удовлетворяют.
Составим изображения некоторых простейших функций.
§ 8.33 Изображение постоянной. Требуется найти изображение функции /(/) = А, где А — постоянная величина. С этой целью в (8.31) вместо /(/) подставим А и проведем интегрирование:
ос
Г(р)= ре-'”
О
Следовательно, изображение постоянной равно постоянной, деленной на р;
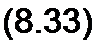 А = А/ р.
А = А/ р.








