Переходные процессы

Дата: 2025-06-02; Просмотры: 16
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

§ 8.1 Определение переходных процессов. Под переходными процессами понимают процессы перехода от одного режима работы элек­трической цепи (обычно периодического) к другому (обычно также периодическому), чем-либо отличающемуся от предыдущего, например амплитудой, фазой, формой или частотой, действующей в схеме ЭДС, зна­чениями параметров схемы, а также вследствие изменения конфигурации цепи.

Периодическими являются режимы синусоидального и постоянного тока, а также режим отсутствия тока в ветвях цепи.

Переходные процессы вызываются коммутацией в цепи. Коммута­ция — это процесс замыкания (рис. 8.1, а) или размыкания (рис. 8.1, б) выключателей.

Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего докоммутаци- онному режиму, к энергетическому состоянию, соответствующему пос- лекоммутационному режиму.

Переходные процессы обычно являются быстро протекающими; дли­тельность их составляет десятые, сотые, а иногда даже миллиардные доли секунды: сравнительно редко длительность переходных процессов дос­тигает секунд и десятков секунд. Тем не менее изучение переходных процессов важно, так как оно дает возможность установить, как дефор­мируются по форме и амплитуде сигналы при прохождении их через уси­лители и другие устройства, позволяет выявить превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изо­ляции установки, увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося периодического процес­са (и вызвать недопустимые механические усилия), а также определить продолжительность переходного процесса.

§ 8.2 Приведение задачи о переходном процессе к решению ли­нейного дифференциального уравнения с постоянными коэффици­ентами. Запишем уравнение по второму закону Кирхгофа для схемы (рис. 8.2) при замкнутом ключе. Сумма падений напряжений на элемен­тах L и R равна ЭДС Е;

ut + R i = Е, или

L — +Ri = E. (8.1)

dt

 


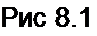Рис. 8.2

Как известно из курса математики, уравнение, содержащее неизвест­ную функцию (в нашем случае /) и ее производные (в нашем случае L ~ ), называют дифференциальным уравнением.

Таким образом, определение тока как функции времени, по сути дела, есть решение дифференциального уравнения.

Известно, что решение дифференциального уравнения — это отыс­кание функции, удовлетворяющей ему. Подстановка этой функции и ее производных превращает дифференциальное уравнение в тождество.

Решение линейных дифференциальных уравнений будем проводить в основном четырьмя методами: классическим, операторным, методом интеграла Дюамеля и методом пространства состояний.

Перед тем как изучать эти методы, необходимо рассмотреть общие свойства линейных цепей при переходных процессах, а также общие за­коны, которым подчиняются переходные процессы в линейных электри­ческих цепях. § 8.3-8.25 посвящены вопросам, имеющим отношение ко всем перечисленным методам расчета переходных процессов; однако часть этих параграфов (см. § 8.3, 8.8, 8.10 и 8.12) следует рассматривать так же, как введение к классическому методу расчета переходных про­цессов.

§ 8.3 Принужденные и свободные составляющие токов и напря­жений. Известно, что общий интеграл линейного дифференциального уравнения равен сумме частного решения неоднородного уравнения плюс общее решение однородного уравнения. Частное решение уравнения (8.1) равно Е/ R (Е — постоянная ЭДС).

Однородное уравнение получаем из исходного, если в нем возьмем правую часть равной нулю. В нашем случае

А—- + /?/ = 0. (8.2)

dt

Решением однородного уравнения является показательная функция вида Ле,,/.

Для всех переходных процессов условимся, что момент / = 0 соответ­ствует моменту коммутации.

Постоянные А и р не зависят от времени. Без вывода дадим их значе­ния для рассматриваемого примера:

A = -E!R и p~-R!L.

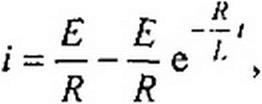Следовательно, решение уравнения (8.1) запишется так:

(8-3)

где EIR—частное решение неоднородного уравнения (8.1);—е '■ — R

общее решение однородного уравнения (8.2). Подстановка (8.3) дает тож­

дество

 


 

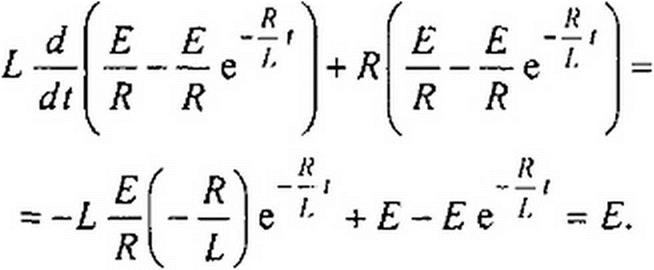Следовательно, (8.3) действительно является решением уравнения (8-1).

Частное решение неоднородного дифференциального уравнения бу­дем называть принужденной составляющей тока (напряжения), а пол­ное решение однородного уравнения — свободной составляющей. При­менительно к рассмотренному примеру принужденная составляющая тока

'пр ~ а свободная составляющая /сп=- —е '■ . Полный ток

 


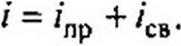Кроме индексов «пр» (принужденный) и «св» (свободный) токи и на­пряжения могут иметь и дополнительные индексы, соответствующие но­мерам ветвей на схеме.

Принужденная составляющая тока (напряжения) физически представ­ляет собой составляющую, изменяющуюся с той же частотой, что и действующая в схеме принуждающая ЭДС. Если в схеме действует принуждающая синусоидальная ЭДС с частотой со, то принужденная составляющая любого тока и любого напряжения в схеме является, соответственно, синусоидальным током (синусоидальным напряжением) частоты ох

Определяются принужденные составляющие в цепи синусоидально­го тока с помощью символического метода (см. гл. 3). Если в схеме дей­ствует источник постоянной ЭДС (как, например, в схеме рис. 8.2), то принужденный ток есть постоянный ток и находят его с помощью мето­дов, рассмотренных в гл. 2.

Постоянный ток через конденсатор не проходит, поэтому принужден­ная составляющая тока через него в цепях с источниками постоянной ЭДС равна нулю. Кроме того, напомним, что падение напряжения на индуктивной катушке от неизменного во времени тока равно нулю.

В линейных электрических цепях свободные составляющие токов и напряжений затухают во времени по,показательному закону е/?/. Так, в рассмотренном примере /св =-~е . С увеличением времени t мно­житель е Л быстро уменьшается. Название «свободная» объясняется тем, что эта составляющая есть решение уравнения, свободного от вы­нуждающей силы (однородного уравнения без правой части).

Из трех токов (полного, принужденного и свободного) и трех напря­жений (полного, принужденного и свободного) основное значение име­ют полный ток и полное напряжение.

Полный ток является тем током, который в действительности протекает по той или иной ветви при переходном процессе. Его можно измерить и записать на осциллограмме. Аналогично, полное напряже­ние — это напряжение, которое в действительности имеется между не­которыми точками электрической цепи при переходном процессе. Его также можно измерить и записать на осциллограмме.

Принужденные и свободные составляющие токов и напряжений во время переходного процесса играют вспомогательную роль; они являются теми расчетными компонентами, сумма которых дает действительные величины.

Здесь следует еще раз обратить внимание на тот факт, что при лю­бых переходных и установившихся процессах соблюдают два основных положения: ток через индуктивную катушку и напряжение на конденса­торе не могут изменяться скачком*[III].

§ 8.4 Обоснование невозможности скачка тока через индуктив­ную катушку и скачка напряжения на конденсаторе. Доказательство того, что ток через индуктивную катушку не может изменяться скачком, проведем на примере схемы на рис. 8.2. По второму закону Кирхгофа

Доказательство того, что напряжение на конденса­торе не может изменяться скачком, проводится анало- ______________________

гично.

Обратимся к простейшей цепи с конденсатором (рис. 8.3). Составим для нее уравнение по второму L—

закону Кирхгофа при замыкании ключа:

R i + ис - Е,

где Е — ЭДС источника, конечная величина; ис — напряжение на кон­денсаторе.

. - dur

Так как i - С ——, то

dt

(8.4)

Если допустить, что напряжение ис может измениться скачком, то duc

—» —i—> oo и левая часть (8.4) не будет равна правой части. Отсю­да следует, что допущение о возможности скачкообразного изменения напряжения на конденсаторе противоречит второму закону Кирхгофа.

 


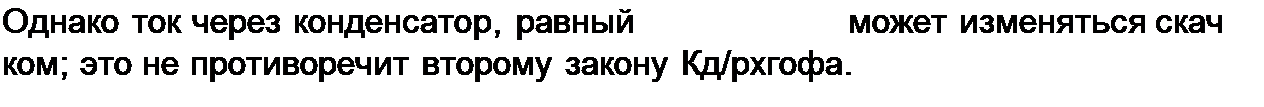ком; это не противоречит второму закону Кирхгофа.

Из указанных двух основных положений следуют два закона (прави­ла) коммутации.

§ 8.5 Первый закон (правило) коммутации. Ток через индук­тивный элемент L непосредственно до коммутации /7(0„) равен току через этот же индуктивный элемент непосредственно после коммута­ции /Л(0+):

(8-5)

Время t = 0_ представляет собой время непосред­ственно до коммутации, / = 0+ — после коммутации (рис. 8.4). Равенство (8.5) выражает собой первый за­кон коммутации.

§ 8.6 Второй закон (правило) коммутации. Обозначим напряжение на конденсаторе непосредственно до коммутации мг(0_), а напряжение на нем непосредственно после коммутации иг(0+).

В соответствии с невозможностью скачка напряжения на конденса­торе

wr(0_) = ис(0+).

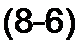Равенство (8.6) выражает собой второй закон коммутации.

Перед тем как приступить к изучению методов расчета переходных процессов, необходимо условиться о некоторых дополнительных опре­делениях.