Колебание, в котором изменяется только амплитуда Л, а угловая час­тота со и фаза у неизменны, называют колебанием, модулированным по амплитуде.

Дата: 2025-06-02; Просмотры: 16

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Колебание с изменяющейся угловой частотой to, но неизменными амплитудой А и фазой у называют колебанием, модулированным по ча­стоте.

Колебание, в котором изменяется только фаза у, а амплитуда А и угловая частота со неизменны, называют колебанием, модулированным по фазе.

Простейшим амплитудно-модулированным (АМ) является колебание, в котором амплитуда модулирована по закону синуса:

/(О = А_о (1 + т sin Q /) sin(co t + ц/),

где т — глубина модуляции (как правило, т < 1), Q — частота модуля­ции (Q «к со).

График AM-колебания показан на рис. 7.13, а (огибающая показана штриховой линией).

Огибающая

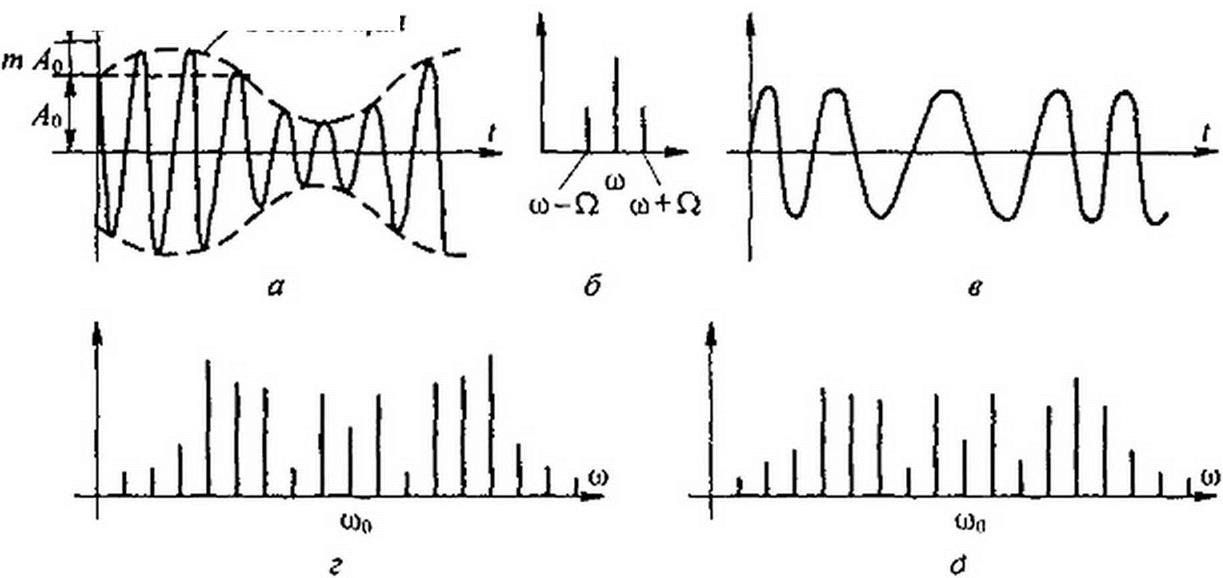
Рис. 7.13

Если воспользоваться известным из тригонометрии тождеством

sin a sin р = — cos(a - Р) - — cos(a + р),
2 2

то колебание

A,(i + т sin Q t) sin(co t + у)

можно представить в виде суммы трех колебаний:

f (/) - А_о sin(o) t + \у) + ——- cos((co ~ Q) t + - ^m - - cos((co + Q) / + \y).

2 2

Частоту co называют несущей, а частоты (co-£7) и (co + Q) — боко­выми. Спектр AM-колебания изображен на рис. 7.13,6. Действующее значение функции f(t) в соответствии с формулой (7.11) равно

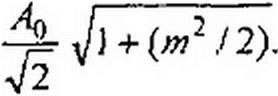
Пример 74. Разложить на составляющие функцию f(t) = 20(1 + 0,6 sin 10³ /) sin 10⁵ t. Решение. Боковые частоты

<о-Я = 99Ю³; w+Q = lO|IO³;

tn Aq (2 = 6.

Следовательно,

f(t) = 20 sin 10^s t + 6 cos(99 -10³ /) - 6 cos(l 01 • 10³ r).

Амплитуды колебания боковых частот при AM-колебании зависят от глубины модуляции nt, но не зависят от частоты модуляции Q.

Ширина полосы частот, занимаемой AM-колебанием, не зависит от т и равна (со + Q) - (со - <2) = 2 Q.

Рассмотрим спектры частотно-модулированных (ЧМ) и фазомодули- рованных (ФМ) колебаний. Форма колебаний качественно показана на рис. 7.13, в.

Аргумент синусоидально изменяющейся функции /(f) обозначим а(/). Тогда

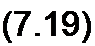/(/) = A sin(a(O),

a(f) можно интерпретировать как угол, на который повернется враща­ющийся вектор на комплексной плоскости за время /. Угловая частота поворота этого вектора со = г/сх(/)/ dt. В том случае, когда о) = со_о = const,

a(f) = jco_o dt = /; j\t) = A sinco_o t.

При частотной модуляции частота © изменяется и равна <о_о + Део <p(f). При этом

«(/) = {(<о_о + Део <p(f)) dt ~ ео_о t + До Jep(f) dt.

При ep(f) = cosQ t

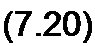a(f) = co_o t + у sin <11,

где у^Део/Q —глубина модуляции. Таким образом,

/(/) / А - sin(eo₀ + у sin Q f) = sin ео f cos(y sin О f) + cos eo₀1 sin(y sin Q f),

HO

•X

sin(y sin О /) = 2 £ (Y) ^sin(2 л +1)

oQ

cos(y sin Q /) = J₀(y) + 2 £ J_2M(y) cos2 n Q t,

л₽0

где J* (у) — бесселева функция А-го порядка от действительного аргу­мента у’\ Графики трех бесселевых функций при А=0,1,2 изображе­ны на рис. 7.14,

После преобразований

о?

/(/) / А = J_Q (у) sin ео₀ / + £ (-1 )^к J_k (у) sin(eo₀ - к О) t +

(7.21)

оО

⁺ Хл<г) sin((o₀ - к Q) /.

Теоретически полоса частот, занимаемых ЧМ-колебанием, равна бес­конечности. Однако если учесть, что с ростом к. значение J _к (у) быстро уменьшается, и в равенстве (7.21) отбросить слагаемые рядов, амплиту-

’’Обшее выражение для бесселевых функций приведено в § 15.14.

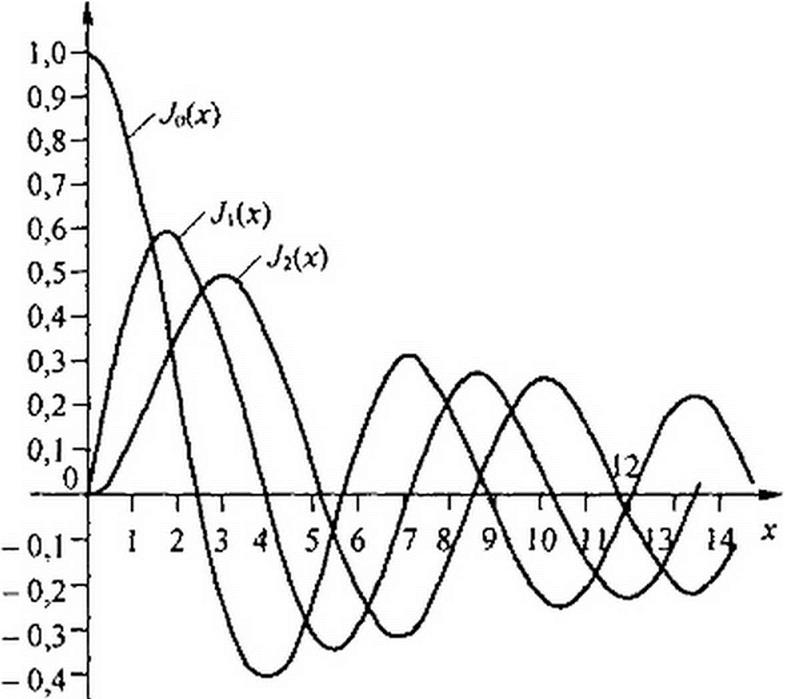
Рис. 7.14

ды которых меньше 0,01, чему соответствует А>у, то ЧМ-колебание практически занимает полосу частот:

(<о₀ + к Q) - (о)_о - к О) = 2 A Q » 2 у О = 2(Д (о/ О) Q = 2 Дох

Ширина ее зависит от глубины модуляции Део и не зависит от часто­ты модуляции Q. Амплитуды боковых частот зависят от До и О. Спектр ЧМ-колебания при у = 5 показан на рис. 7.13,2.

При фазовой модуляции угловая частота о₀ неизменна и меняется только фаза ц/(г). Следовательно,

Приняв

получим

/(/) = A sin(o₀ t + \у_м cosQ t).

Амплитуда фазы от частоты модуляции Q не зависит.

Опустив выкладки, определим, что амплитуды боковых частот зави­сят от а ширина полосы частот 2 к Q * 2 Q — от у_т и <2. Спектр ФМ-колебания при к Q = 5 изображен на рис. 7.13, <3.

Из рис. 7.14 видно, что если х 1, то a Jj(x)~x/2. От­

сюда следует, что в ЧМ-колебании при у с 1, а в ФМ-колебании при «; 1 можно ограничиться только основной гармоникой to₀ и двумя боковыми <в₀ ±Q, т. е. в этом случае имеет место почти такая же ситуа­ция, что и в АМ-колебании.

Различие будет в том, что при ЧМ и ФМ на комплексной плоскости два вращающихся вектора боковых частот дают в сумме вектор, направ­ленный перпендикулярно неподвижному вектору частоты ш₀, тогда как при АМ векторная сумма двух вращающихся векторов боковых частот будет направлена вдоль неподвижного вектора частоты <о₀. Это разли­чие вызвано разными знаками у временных компонент гармоники час­тоты to_o - <Э.

§ 7.16. Расчет линейных цепей при воздействии модулированных колебаний. Расчет токов и напряжений в линейных электрических це­пях при воздействии на них модулированных колебаний производят для мгновенных значений величин либо для мгновенного значения огибаю­щей. В первом случае расчет проводят путем разложения модулирован­ных колебаний на составляющие, вычисления токов и напряжений от каж­дой из них в отдельности и последующего суммирования соответствую­щих токов и напряжений на основании принципа наложения. При этом ограничиваются теми составляющими, которые существенны в форми­ровании выходной величины.

При воздействии AM-колебания на какую-либо систему точный рас­чет огибающей выходной величины может быть осуществлен по форму­ле интеграла Дюамеля для огибающей (см. § 8.67).

Вопросы для самопроверки

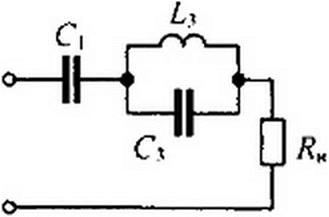
1. В каких случаях следует ожидать возникновения несинусоидальных токов и напря­жений в электрических цепях? 2. Какие виды симметрии несинусоидальных кривых вы знаете и как они сказываются на гармоническом составе? 3. Изложите основные положе­ния. на которых основывается методика расчета линейных цепей при периодических несинусоидальных воздействиях. 4. Входное напряжение w_bX(/) (рис. 7.15. а) содержит

а б в

Рис. 7.15

постоянную составляющую, первую и третью гармоники. Определите С] и через со и чтобы в нагрузку К_и проходила неизменной только первая гармоника, а остальные отсутствовали. (Ответ: С_} = 8 / (9 Z,₅); С₃ = I / (9 о² Aj).) 5. Охарактеризуйте физи­

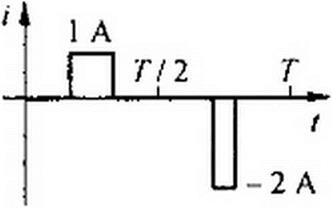
ческий смысл действующего значения несинусоидального тока. 6. Всегда ли самым корот­ким расчетным путем при определении действующего значения несинусоидалыюго тока / является нахождение его по гармоническому составу, по формуле (7.10)? Определить / на рис. 7.15. б. (Ответ: 0JQ1 А.) 7. Приборами каких систем можно измерять: а) действую­щее значение несинусоидального тока; б) среднее по модулю значение; в) амплитудное зна­чение? 8. Определить действующее значение тока / = 5(1 -0,8 sin 100/) sin J ООО г. (Ответ: 4.075 А.) 9. Почему нельзя складывать действующие значения токов различных частот?

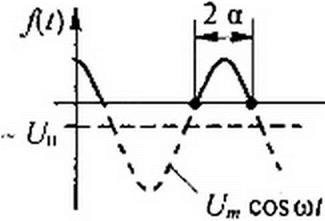
10. Могут ли отдельные слагаемые в формуле активной мощности (7.16) быть отрицатель­ными? 11. При каких ограничениях несинусоидальные токи и напряжения приближенно могут быть заменены эквивалентными синусоидальными? 12. Чем можно объяснить, что при равномерной нагрузке трехфазной системы «звезда—звезда» для протекания токов тре­тьих гармоник необходим нулевой провод? 13. В каком случае возникают колебания, на­зываемые биениями? 14. Охарактеризуйте виды модулированных колебаний и занимаемые ими полосы частот. 15. Нарисуйте графики колебаний, модулированных: а) по амплитуде; б) частоте; в) фазе. 16. На рис. 7.15, в изображена функция f(i) = {-U_Q + cosw/)>0

Она имеет вид положительных косинусоидальных импульсов. Угол отсечки о = arccos(Z7oIU_m). Вывести формулы для постоянной составляющей и амплитуды A-гар­

моники ряда Фурье. (Ответы'. А_о = —— (sin а - a cos а). А”_к ~---------------------------------------------------------------------------------- (sin к а cos а -

* пк(к²-\)

~к cosAa sin а).) 17. Решите задачи 9.9; 9.12; 9.13; 9.15; 9.16; 9.19; 9.21; 9.25.

Глава восьмая