Отношение Ол JUty < -/з, если есть гармоники, кратные трем.
4. При соединении генератора и равномерной нагрузки звездой и отсутствии нулевого провода токи третьих и других гармоник нулевой последовательности не могут протекать по линейным проводам. Поэтому между нулевыми точками приемника О' и генератора О (рис. 7.9) при Zq = оо возникает напряжение
U (TD = ь«п(3<вг+у3)+ E6m sin(6 w f ) + •••.
действующее значение которого
 |
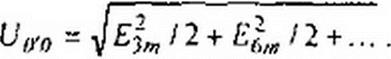5. Если в схеме «звезда—звезда» при равномерной нагрузке фаз сопротивление нагрузки для третьей гармоники обозначить ZH?. а сопротивление нулевого провода для третьей гармоники — Z03 (см. рис. 7 9). то по нулевому проводу будет протекать ток третьей гармоники:
i - е»
1 03 7
■7 .
г 0.1
По каждому из линейных проводов будет протекать ток третьей гармоники /03 / 3. Аналогично находят токи и других гармоник, кратных трем.
Пример 71. Мгновенное значение напряжения фазы А трехфазного генератора
иА =127 sin(o/+ 10°)+ 30sin(3 t) t + 20°)+ 20sin(J I o/ +15°) B.
Определить мгновенное значение линейного напряжения при соединении генератора звездой.
Решение. В линейном напряжении третья гармоника отсутствует. Первые гармоники фаз А и В по фазе сдвинуты на 120°. Поэтому линейное напряжение (JAfi первой гармоники в Уз раз больше фазового напряжения первой гармоники UA и на 30° опережает его по фазе.
Одиннадцатая гармоника (обратная последовательность фаз) линейного напряжения отстает по фазе от одиннадцатой гармоники напряжения фазы А на 30° и в V3 раз больше ее:
uAf) ••= 127 7з sin(fc)/ + 40°) + 20 -Уз sin(l 1 о t - 15°) В.
 |
|
 | |||||
 | |||||
 | |||||
|
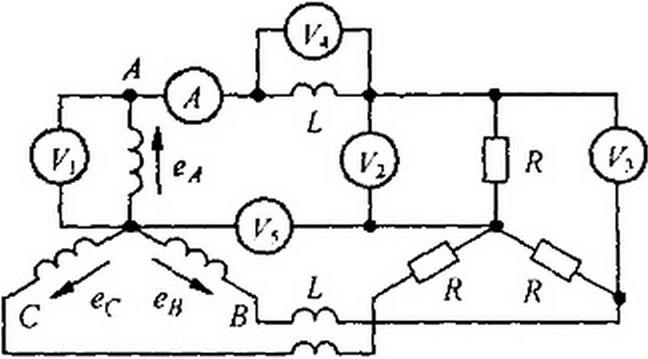
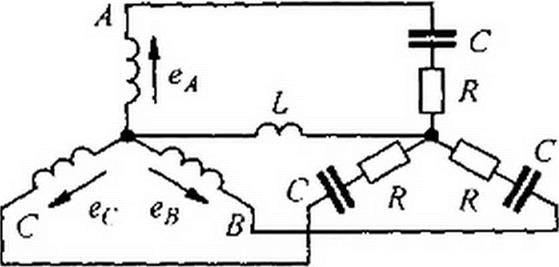
Пример 72. ЭДС фазы А в схеме (рис. 7.10) еА = 170 sin© t + 80 cos 3 со / + 34 cos9 to t B; /? = 9Ом; <иЛ = 2Ом.
Определить показания всех приборов (приборы электродинамической системы)
Решение. Действующие значения ЭДС
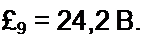=170/Л = 12113; £ч = 56.5 В;
По линейным проводам течет первая гармоника тока:
/, =-' £, /^Я2+(о£)2 = 121/9.2 - 13.2 А.
Показания вольтметров:
Ij = ^Е{ + Е] + EJ = 136 В; Р'а = /( Я, = 13,2 9 = 118.5 В;
И, = Л 118.5 =205 В; Г, = /, © L = 26.4 В; 1\ =-/ff + £g =61.4 В.
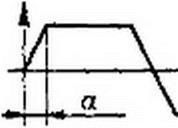
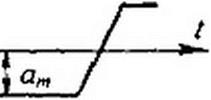
Пример 73. ЭДС каждой фазы генератора (рис. 7.11) изменяется по трапецеидальному закону. а„, = 220 В; а =7/36; нагрузка равномерная; Я = 6Ом; со 7 = 0,5 Ом; |/©С = 12Ом. Определить мгновенное значение тока по нулевому проводу, пренебрегая гармониками тока выше седьмой.
Р е ш е н и е. С помощью табл. 7.1 запишем разложение трапецеидальной ЭДС:
е . = -4- (sin 10° sin© t + ~sin30° sin 3 w/ + — sin50° sin5 co I + “ sin70° sin 7 © t).
A л 9 25 49
— л
Следовательно,
eA = 274 sin co ( + 89.3 sin 3 w/ + 49.5 sin 5 © / 4 30,9 sin 7 ©/.
По нулевому проводу протекает только третья гармоника тока: где
 |
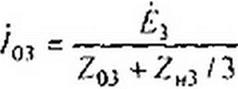=89,3/72 =63.3 В; Z05 = 1,5 j; Z^=6~4/. Z„/3 = 2-у 1,33;
/0} = 63,3 / (1,5 / + 2 - j 1.33) = 31.8 е’4“40' А.
Мгновенное значение тока = 44.8 sin(3 о i - 4°40') Л.
§ 7.14 Биения. Колебательный процесс, получающийся в результате сложения двух синусоидальных колебаний с равными амплитудами А и близкими, но не равными частотами СО] и со2, дает колебание, которое называют биением. Пусть /(/) = A sin со। t + A sin <о21-
|
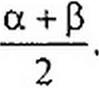
Воспользуемся известным тригонометрическим преобразованием
sin о. + sin В = 2 cos —
2
|
Следовательно, /(г) можно представить следующим образом:
f(t) = 2 A cos О / sin со
где
Q = (о)] -о>2)/2;
со - (сог + со2)/2 (Q «: со).
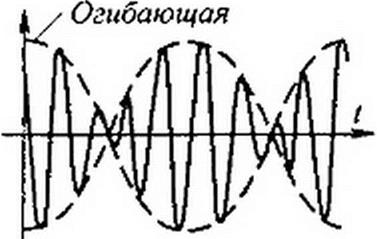
График результирующего колебания изображен на рис. 7.12. Амплитуда колебания изменяется по закону 2 y/cosQz. Огибающая колебаний показана штриховой линией.
Возникновение биений при сложении двух синусоидальных колебаний с равными амплитудами и близкими (но не равными) частотами используется на практике в различных целях, в частности для того, чтобы установить, что складываемые колебания имеют неодинаковые частоты.
§ 7.15 Модулированные колебания. При передаче информации широко применяют модулированные колебания. Модулированным колебанием f(t) = A sin(co / + у) называют колебание, в котором амплитуда Л, частота со, фаза или те и другие вместе изменяются во времени.