§ 7.13'*. Особенности работы трехфазных систем, вызываемых гармониками, кратными трем.

Дата: 2025-06-02; Просмотры: 14

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

ЭДС каждой фазы трехфазного трансформатора или трехфазного генератора часто оказываются несинусоидальными. Каждая ЭДС (е^, е₍-) повторяет по форме осталь­

ные со сдвигом на одну треть периода 773 и может быть разложена на гармоники. По­стоянная составляющая обычно отсутствует.

Пусть ^-гармоника ЭДС фазы А

= b'^sin(A wz + v*).

Так как ЭДС фазы В отстает от ЭДС фазы А на 773, а ЭДС фазы С опережает ЭДС фазы А на Т/3, то А-гармоники ЭДС фаз В и С соответственно

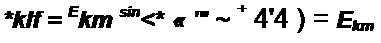sin(A- tor- 120® к ч-Ч»*)',

e_kC - ^km sin(к ы t + 120® к + 4'*);

.2nT 2 it
k<i)T^=k = к — = 120 к

ГЗ 3

Если к = 1,4.7,10, то i-гармоника ЭДС фазы В отстает на 120® от ^-гармоники ЭДС фазы А. Следовательно, I-, 4-, 7-, 10-я гармоники образуют систему прямой последова­тельности фаз (что понимают под прямой последовательностью фаз — с.м. § 6.20).

Если к - 2,5. 8, И, то £-! армоника ЭДС фазы В опережает .fc-гармояику ЭДС фазы А на 120®. Следовательно. 2-, 5-, 8-я и т. д. гармоники образуют систему обратной последовательности.

Гармоники, кратные трем (к = 3,6,9....). образуют систему нуле­вой последовательности, т. е. третьи гар­моники ЭДС всех т рех фаз совпадают по фазе (3-120° = 360®):

^е ЗА = ^еЗН = ^еЗС “ ^Е>т W Z + у , )

Шестые гармоники ЭДС также со­впадают по фазе и т. д.

Совпадение по фазе третьих гармо­ник ЭДС всех трех фаз проиллюстриру­ем графически. На рис. 7.6 ЭДС е_А, е_н, е₍- представляют собой три фазные ЭДС трехфазного генератора Они имеют пря­моугольную форму и сдвинуты относи­тельно друг друга на одну треть периода

(Г/3) основной частоты. На том же рисунке показаны 1-я и 3-я гармоники каждой ЭДС. Из рисунка видно, что третьи гармоники ЭДС действительно находятся в фазе.

Рассмотрим особенности работы трехфазных систем, вызываемые гармониками, крат­ными трем.

’’Материал §7.13 особенно необходим студентам электроэнергетических и электро­механических специальностей.

1. При соединении обмоток трехфазного генератора (трехфазного трансформатора) тре­угольником (рис. 7.7, а) по ним протекают токи гармоник, кратных трем, даже при отсут­ствии внешней нагрузки. Алгебраическая сумма третьих гармоник ЭДС равна 3 £₃.’’ Обо­значим сопротивление обмоток каждой фазы для третьей гармоники Z₃, тогда ток тре­тьей гармоники в треугольнике 7₃ = 3 £₃ /3 Z₃ = Ё₃/ Z₃. Аналогично, ток шестой гармо­ники /₆ = £₆/ Z^, где Ё₆ — действующее значение шестой гармоники фазовой ЭДС; Z₆ — сопротивление фазы для шестой гармоники.

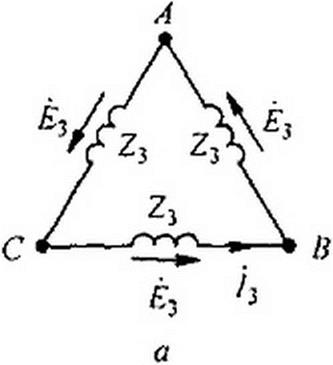Действующее значение тока, протекающего по замкнутому треугольнику в схеме на рис. 7.7, а'.

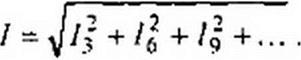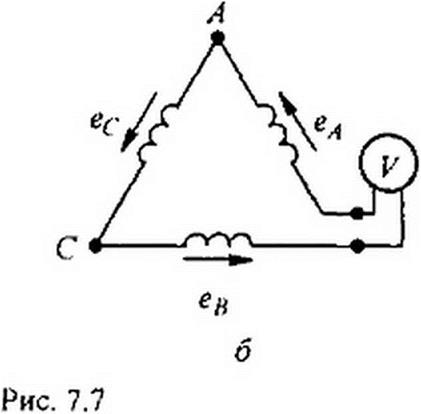
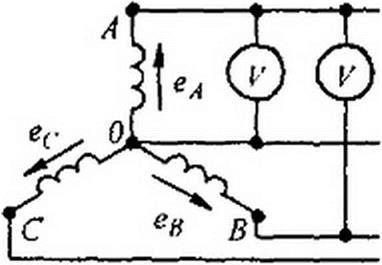
2. Если соединить обмотки трехфазного генератора (трехфазного трансформатора) в открытый треугольник (рис. 7.7, 6). то при наличии в фазовых ЭДС гармоник, кратных трем, на зажимах т и и будет напряжение, равное сумме ЭДС гармоник, кратных трем:

U ~ Eim S’n(3e I + Ч'зН Е_Ьт sin(6 (ОГ + \|/₆) + ... .

Показание вольтметра в схеме рис. 7.7. о

(7=3^+^+

3. В линейном напряжении независимо от того, звездой или треугольником соедине­ны обмотки генератора (трансформатора), гармоники, кратные трем, отсутствуют, если нагрузка равномерна.

Рассмотрим сначала схему соединения трехфазного источника ЭДС треугольни­ком (рис. 7.7, а) при отсутствии внешней нагрузки. Обозначив потенциал точки А. Фйз — потенциал точки В по третьей гармонике, получим ф_л3 =Ф«з ⁺ Ё₃ -I₃ Z₃. Но Ё₃ = !₃ Z₃, следовательно, ф_л3 =Фдз ^Р^и наличии равномерной нагрузки, соединенной треугольником, каждая фаза генератора (трансформатора) и параллельно ей присоединен­ная нагрузка могут быть заменены эквивалентной ветвью, с некоторой ЭДС Е'₃ и сопро­тивлением Z\. На полученную схему можно распространить вывод, сделанный для слу­чая отсутствия внешней нагрузки.

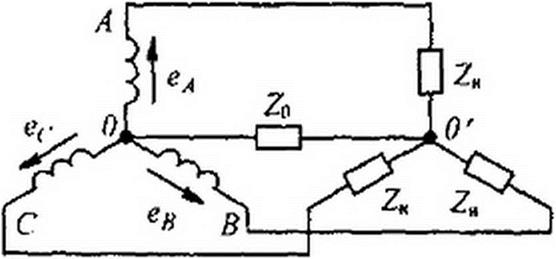
При соединении звездой трехфазного источника ЭДС (рис. 7.8) линейное напряжение третьей гармоники равно разности соответствующих фазовых напряжений. Так как тре­тьи гармоники в фазовых напряжениях совпадают по фазе, то при составлении этой раз­ности они вычитаются.

В фазовом напряжении могут присутствовать все гармоники (постоянная составляю­щая обычно отсутствует). Следовательно, действующее значение фазового напряжения

‘‘Алгебраическая сумма первых гармоник ЭДС и всех гармоник ЭДС, не кратных трем, равна нулю, поэтому от перечисленных гармоник при отсутствии нагрузки по замкнуто­му треугольнику ток протекать не будет.

(/_ф = ^|^{2 + ++} "Л ■■• •

В линейном напряжении схемы (см. рис. 7.8) отсутствуют гармоники, кратные трем, поэтому

и_я = 7з + О'; + uf.