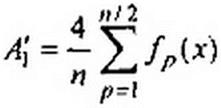Кривая, подобная кривой на рис. 7.1, б, обладает симметрией отно­сительно оси ординат и удовлетворяет условию — /(-*) - /(х).

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если кривую, лежащую левее оси ординат, зеркально отразить относительно оси ординат, то полученная кривая совпадает с кривой, лежащей правее оси ординат. При разложении таких кривых в ряд Фу­рье отсутствуют синусные (Я₍' = Я, - Я₃ =... - 0) составляющие, т. е. присутствуют лишь косинусные и постоянная составляющие.

Таким образом, кривые типа кривой рис. 7.1, б можно разложить в ряд

/(х) - Я_о + Я[ cosx + Я'₇ cos2 х + Я₃ cos3 х +...

Кривые типа кривой на рис. 7.1, в удовлетворяют условию -/(-х) = /(х), их называют кривыми, симметричными относительно начала координат. Разложение их в ряд Фурье имеет такой вид:

/(х) = Я)' sin х + А'₂ sin 2 х + Я₃ sin 3 х +...

§ 7.4 О разложении в ряд Фурье кривых геометрически правиль­ной и неправильной форм. Встречающиеся в электротехнике периоди­ческие кривые можно подразделить на две группы:

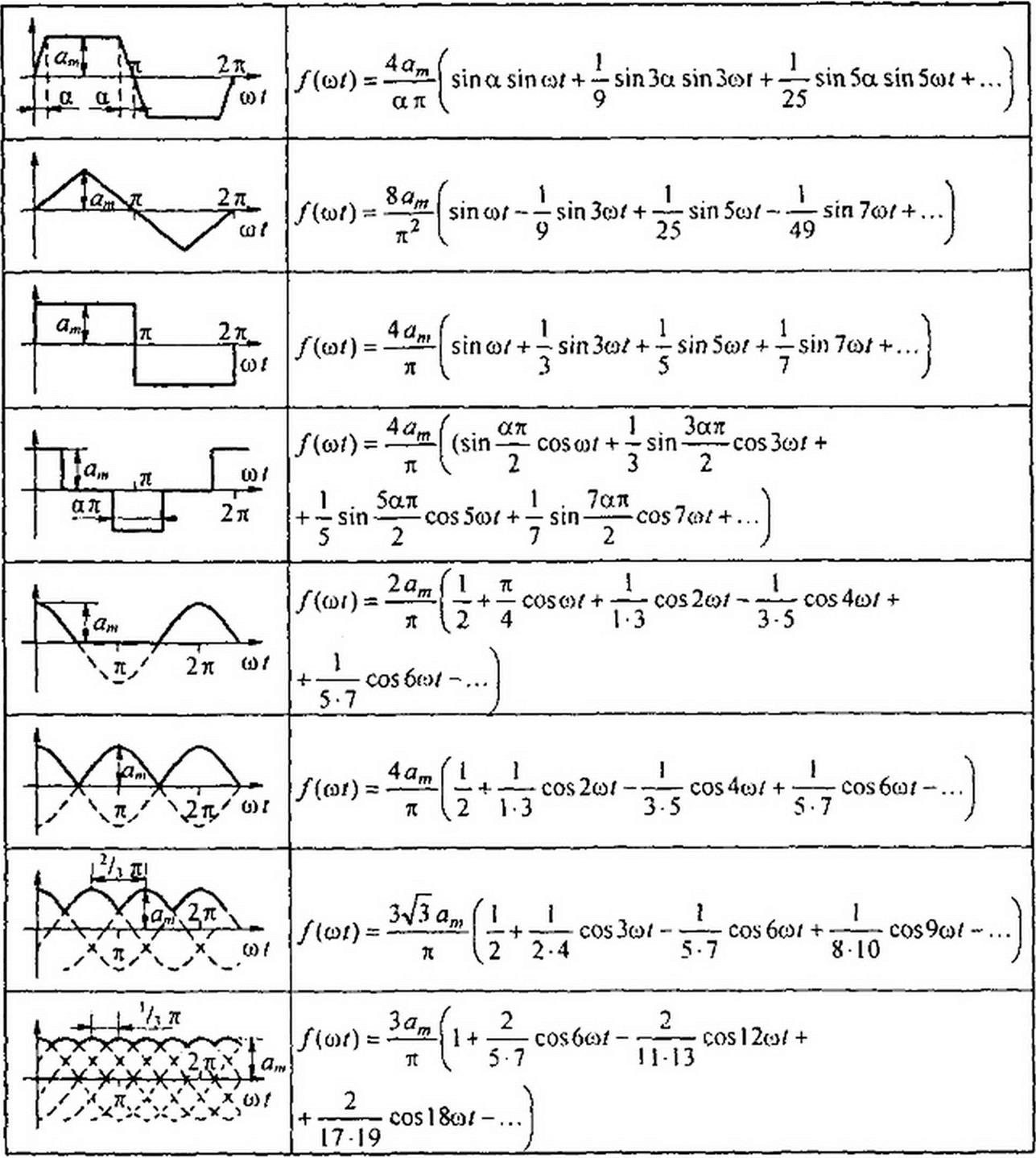
1) кривые геометрически правильной формы, например трапецеидаль­ной, треугольной, прямоугольной и т. п.; разложение их в ряд Фурье дано в табл. 7.1, где вместо х записано си/;

2) кривые произвольной (геометрически неправильной) формы; чаще всего они заданы в виде графика; разложение их в ряд Фурье произво­дят графически (графоаналитически).

3) .5. Графический (графоаналитический) метод определения гармоник ряда Фурье. Графический метод определения гармоник ряда Фурье основан на замене опреде­ленного интеграла суммой конечного числа слагаемых. С этой целью период функции Дх), . 2 л

равный 2 я, разбивают на п равных частей Дх-— и интегралы заменяют суммами.

п ^п

По определению, постоянная составляющая

¹ v г /

- /.У/Z ’

2л “ ' и Р=»

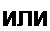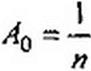где р — текущий индекс, принимающий значения от 1 до п: /_/?(х) — значение функции /х) при х = (р-0.5) Дх. т е. в серединер-го интервала.

Амплитуда синусной составляющей А-гармоники ряда

2 п _п

4=— Г$тАх</х*-^-У/'(х) — sin кх,
^л о ^п

ИЛИ

2 ^п

^ = - y.fp(x) sin,, к х; (7.6)

/7 p = t

амплитуда косинусной составляющей А-гармоники

2 "

4 = -^/^Wcos,,* х, (7.7)

^Л />=н

где sin,, А х и cos,, кх — соответственно значения функций sin Ах и cosAx при х = (р •• 0,5) Ах, т. с. в середине р-го интервала.

При расчетах по (7.5)—(7.7) обычно достаточно разделить период на л = 24 или 18 частей, а в некоторых случаях и на меньшее число.

Перед тем как производить графическое разложение в ряд, необходимо выяснить, не обладает ли раскладываемая функция симметрией относительно осей координат (см. § 7.3). Наличие того или иною вида симметрии позволяет до проведения разложения предска­зать. какие гармоники следует ожидать. Так, если кривая /(х) симметрична относитель­но оси абсцисс, то постоянная составляющая Л_о и все четные гармоники отсутствуют, а вычисляя А'_к и А"_к при нечетных А. следует учесть, что £/,,(x)sin,, А х за первый полу­период равна сумме £/,,(х) sin,, к х за второй полупсриод.

Знак углов у* в формуле (7.4) зависит от знаков А'_к и А’_к. При построении гармо­ник на общем графике необходимо учитывать, что масштаб по оси абсцисс для А-гармо- ники должен быть взят в А раз большим, чем для первой гармоники.

Так. если некоторый отрезок на оси абсцисс для первой гармоники выражает собой угол л/3. то тот же отрезок для третьей гармоники выражает собой уюл. в 3 раза боль­ший, т е. 3л/3 = л.

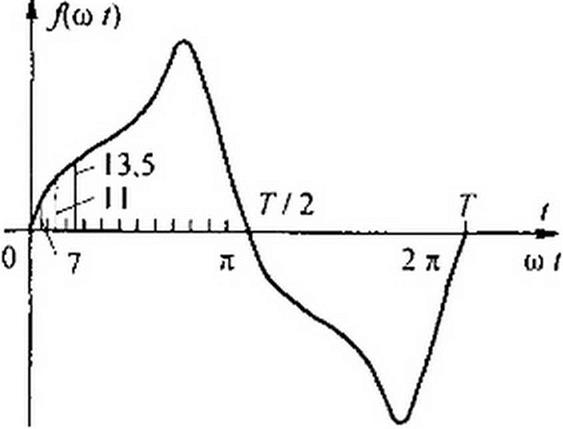
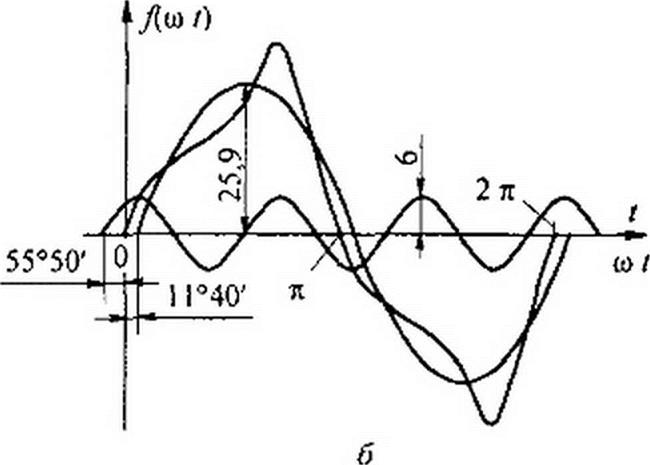
Пример 64. Найти первую и третью гармоники функции /(х), изображенной на рис. 7.2, а Значения ординат функции /(х) за первый полупсриод при разбивке периода на п = 24 части — следующие:

1 2 3 4 5 6 7 8 9 10 11 12

7 II 13.5 15.4 17.4 20.5 25.4 32,5 27,7 19,2 10 5

Р стен и е. Так как кривая симметрична относительно оси абсцисс, то А_о = 0 и ряд будет состоять только из нечетных гармоник.

Амплитуда синусной составляющей первой гармоники

2 У* * 4

/1)' = - £//,(*) sin,, X = - £/,, (х) sin_p х,

^П D-\

А\ = — (7 sin 7°30' +11 sin 22’30' +13,5 sin 37°30' +

¹ 24

+15,4 sin 52’30' + 17,4 sin 67’30' + 20,5 sin 82’30' +
+ 25,4 sin 97’30' + 32,5 sin 112’30' + 27,7 sin 127’30' +
+19.2 sin42’30' + 10 sin 157’30' + 5 sin 172’30') % 25.3.

Амплитуда косинусной составляющей первой гармоники

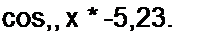Амплитуда синусной составляющей третьей гармоники

А', зЛ-V/ (х)sin,,3x^3,47.

■> 24 х—' р р

Амплитуда косинусной составляющей третьей гармоники

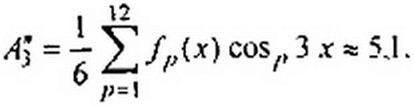
Амплитуда первой гармоники А_} - ^{А{)² ^(А^)² =25,9. Ташспсугла ц/,. на который начало первой гармоники смещено относительно начала кривой /(х),

(gVl = Я]’/А! =-5,23/25,3 = -0,206; Vi =-П°40'.

Амплитуда третьей гармоники

А = J(Atf+(A'i)² = 6; tg у J = Л? / А\ = 1,47; _{v 3} = 55’50'

Следовательно, если ограничиться третьей гармоникой, то /(« /) -■ 25,9sin(o / -11’40') + 6sin(3 л>/ + 55’50').

На рис. 7.2, б изображены первая я третья гармоники полученного ряда, а также ре­зультирующая (суммарная) кривая. Ее можно сопоставить с кривой на рис. 7.2. а.

§7.6. Расчет токов и напряжений при несинусоидальных источ­никах питания. До проведения расчета вынуждающие силы (ток источ­ника тока или ЭДС источника ЭДС) должны быть представлены рядами Фурье.

Согласно принципу наложения, мгновенное значение тока любой вет­ви схемы равно сумме мгновенных значений токов отдельных гармоник. Аналогично мгновенное значение напряжения на любом участке схемы равно сумме мгновенных значений напряжений отдельных гармоник на этом участке. Расчет производят для каждой из гармоник в отдельности с помощью уже известных приемов. Сначала рассчитывают токи и на­пряжения, возникающие от действия постоянной составляющей ЭДС или источника тока, затем токи и напряжения от действия первой гармони­ки, после чего от второй, третьей и т. д.

При расчете токов и напряжений, возникающих от действия постоян­ной составляющей ЭДС, необходимо иметь в виду, что падение напря­жения на L при постоянном токе равно нулю, а также что постоянный ток через конденсатор С не проходит.

При расчете следует учитывать, что индуктивное сопротивление X_} растет прямо пропорционально частоте. Поэтому для А'-гармоники X _tJc в к раз больше, чем для первой гармоники X_1А :

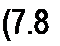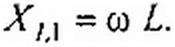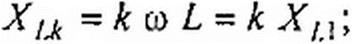Емкостное сопротивление уменьшается с ростом частоты, поэтому для

А:-гар.моники Х_ск в к раз меньше, чем для первой гармоники А'_<;] :

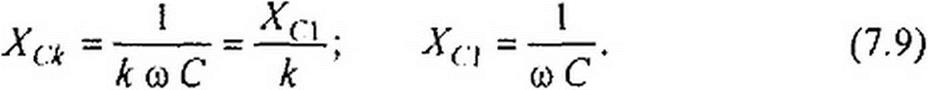Для каждой гармоники можно построить векторную диаграмму. Од­нако откладывать на векторной диаграмме токи и падения напряжения различных частот и тем более векторно складывать токи и падения на­пряжения различных частот недопустимо, поскольку угловые скорости вращения векторов разных частот неодинаковы.

Резистивные сопротивления, если частоты не очень велики, полага­ют от частоты не зависящими.

При расчете каждую гармонику выражают комплексным числом. Сум­мирование одноименных гармоник производят сложением комплексных чисел или векторов на комплексной плоскости, т. е. так же, как это дела­лось в гл. 3.

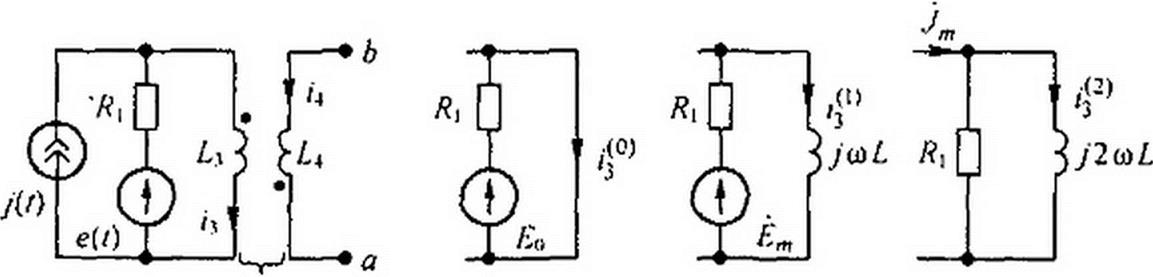
Решение. Положительные направления для токов выберем в соответствии с рис. 7.3. а. По второму закону Кирхгофа

- ^4-г-+ Л/—i = 0.
dt at

но /₄ = 0, поэтому = -М

Воспользуемся принципом наложения и найдем составляющие тока от каждого источника в отдельности.

Схема рис. 7.3, б служит для расчета токов от действия постоянной составляющей ЭДС. Левая ветвь схемы разомкнута, так как в ней включен источник тока с бесконечным со­противлением. Правая ветвь короткозамкнута, так как индуктивность для постоянного тока имеет нулевое сопротивление. При этом = 1 А

Первую гармонику тока найдем, используя схему на рис. 7.3, в:

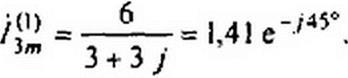
Вторую гармонику тока вычислим в соответствии со схемой на рис. 7.3, г:

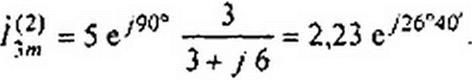
Мгновенное значение тока i_} равно сумме мгновенных значений:

6 = 4^{0> + +} 'з²⁾ = ’ + sin(w / - 45°) + 2,23 sin(2 о / + 26’40') А.

Напряжение

= -М = 1.41 cos(<t> I - 45°) - 4,46 cos(2 wt + 26’40') В. d(

§ 7.7 Резонансные явления при несинусоидальных токах. Как известно из гл. 3, резонансным режимом работы электрической цепи, содержащей один или несколько индуктивных и один или несколько емкостных элементов, называют такой режим, при котором ток на входе совпадает по фазе с действующей на входе ЭДС.

Если действующая ЭДС несинусоидальна, то в электрической цепи могут возникать резонансные режимы (резонансы токов или напряжений) не только на первой, но и на высших гармониках.

Условимся под резонансом на Л-гармонике понимать такой режим работы, при котором ток А-гармоники на входе цепи по фазе совпадает с А-гармоникой, действующей на входе ЭДС (но при этом токи остальных гармоник не совладают по фазе с вызвавшими их ЭДС).

Если учитывать активные сопротивления индуктивных катушек, то условие возникновения резонанса для какой-либо гармоники заключает­ся в том, что реактивная составляющая входного сопротивления для этой гармоники должна быть равна кулю.

Исследование резонансных явлений при несинусоидальных токах ча­сто производят, полагая активные сопротивления индуктивных катушек равными нулю. В этом случае входное сопротивление при резонансе токов равно бесконечности, а входное сопротивление при резонансе на­пряжений равно нулю.

При возникновении резонансного и близкого к нему режима на какой- либо высшей гармонике токи и (или) напряжения этой гармоники могут оказаться большими, чем токи и напряжения первой гармоники на этих участках цепи, несмотря на то что амплитуда соответствующей высшей гармоники ЭДС на входе схемы может быть в несколько раз меньше ам­плитуды первой гармоники ЭДС.

Пример 66. В схеме (рис. 7.4) катушка обладает индуктивно­стью /,₂. Полагая активное сопротивление индуктивной катушки равным нулю, найти, при каких значениях емкостей (?_t и С₂ вход­ное сопротивление схемы для первой гармоники равняется нулю, а для девятой — бесконечности.

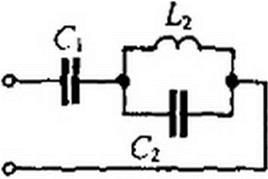
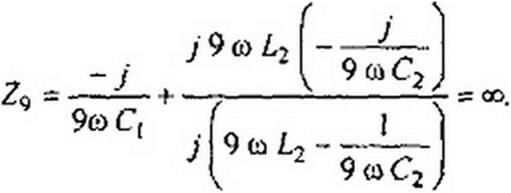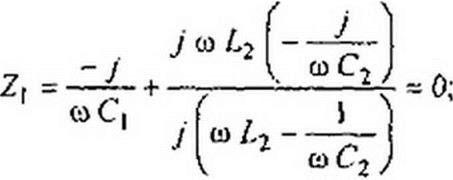Решение:

~ I , I 81

Совместное решение дает ----------- = 8lcoL₎; -------------------------------------------------------- = —

wCj wCj 80

§ 7.8 Действующие значения несинусоидального тока и несину­соидального напряжения. По определению (см. § 3.2)» квадрат дейст­вующего значения тока / выражают через мгновенное значение тока i следующим образом:

1^г=- dt.

^Т1

Если ток

^{/ = /}о ^{+ /}»« sin(cor + 4/})+ /_2/м sin(2<d/ + \p₂) + ..., то

/² = /₀² + X ^f k,4 sin²(А со / + Ф J + *=1

Но

С _? Т

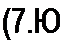Jsin²(£ со / + dt = —; о т

Jsin(/? е>/ + y_p)sin(q to 1 + ф₉) dt = 0. о

Поэтому

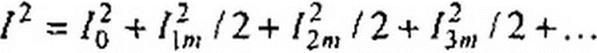
Так как амплитуда А-гармоники тока 1_кт в раз больше действую­щего значения тока А-гармоники 1_к, то

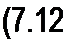/ - /о + /j² + 7₂^{2 +} з^{2 +}

Следовательно, действующее значение несинусоидального тока рав­но корню квадратному из суммы квадратов постоянной составляющей тока и действующих значений отдельных гармоник. От угла сдвига фаз ц_к действующее значение тока не зависит.

Аналогично действующее значение несинусоидального напряжения U равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник:

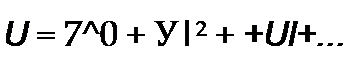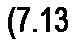Пример 67. На входе двухполюсника н = 100 + 80 sin(c')/ч-ЗО⁰)-»-60 sin (Зо>/+20°) + +50sin(5<a i + 45°) В; i = 33,3 +17.87 sin(a t - 18°) + 5.59 sin(5w t +120°) А. Найти их дей­ствующие значения.

Решение.

U = 71 ОО² + 80² 12 + 60²”/2 + 50- /2 = 127.1 В;

I ~ д/зз.2² + 17.87³/2 + 5,59²/2 = 35.6 Л.

§ 7,9. Среднее по модулю значение несинусоидальной функции. Под средним по .модулю значением функции понимают среднее значение модуля этой функции за период:

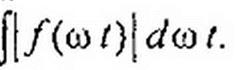В отличие от действующего значения оно зависит от значений у_к.

Пример 68. Дана функция, не содержащая постоянной составляющей и четных гар­моник и не изменяющая знака в течение каждого полупсриода. Определить ее среднее по модулю значение.

Решен и е. Разложим заданную функцию в ряд Фурье.

i-J_lm sin(w/ + yj)⁺ sin(3or+ \|/₃)+/_5я, sin(5 co t + \|/$) +...

После интегрирования получим

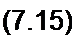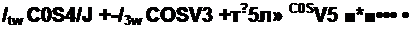§ 7.10 Величины, которые измеряют амперметры и вольтметры при несинусоидальных токах. Несинусоидальные токи и напряжения измеряют приборами различных систем. Принципы действия этих при­боров рассматривают в курсе электрических измерений. Поэтому здесь упомянем лишь, какие величины измеряют вольтметры и амперметры различных систем.

Приборы электромагнитной, электродинамической и тепловой систем реагируют на действующее значение, магнитоэлектрические приборы с выпрямителем — на среднее по модулю значение величины, магнитоэлек­трические без выпрямителя — на постоянную составляющую, амплитуд­ные электронные вольтметры — на максимальное значение функции.

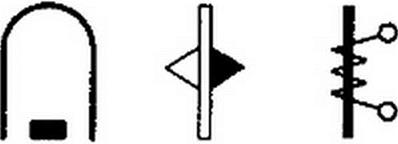
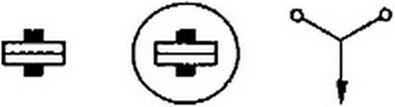
Напомним, что на лицевой стороне измерительного прибора всегда имеется условный значок, свидетельствующий о том, к какой системе относится данный прибор. На рис. 7.5 приведены некоторые из них: а — магнитоэлектрическая с подвижной рамкой; б — магнитоэлектри­ческая с подвижным магнитом; в — электромагнитная; г — электроди­намическая; д — ферродинамическая; е — тепловая; ж — электроста­тическая; з — магнитоэлектрическая с выпрямителем.

В настоящее время обозначения несколько изменены: измерительные приборы электромагнитной системы стали обозначать тепловой си­стемы — значком электростатической — детекторной--------------

§ 7.11 Активная и полная мощности несинусоидального тока. Под активной мощностью Р несинусоидального тока понимают среднее зна­чение мгновенной мощности за период первой гармоники:

1 ?

Р = — Гм i dt.

Т ^J
‘ о

Если представить напряжение и и ток i рядами Фурье:

U = U_o + и_[п, sin(oo t + ц/|) + U_2n) sin(2 со t + ф₂) ⁺ Щт sin(3 оо / + ф₃) + ...;

i = k ⁺ sinCow + V] -<p|) + /_2m sin(2 со z ц/₂ -ф₂) +

+ /_3w sin(3 to t + - фз) +...,

подставить эти ряды под знак интеграла и проинтегрировать, учтя соот-

ношения (7.10), то можно получить

Р = и₀ /о + l/j /) COSф] +и₂ h С05ф₂ + Uy /3 СО5фз + ... . (7.16)

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник.

Полная мощность S равна произведению действующего значения несинусоидального напряжения на действующее значение несинусоидаль­ного тока:

(7.17)

где

и=^u₀²+y_l²+i/₂²+i/₃²+...;
/=;/²₊/,²₊/²₊/²₊....

Пример 69. Определить Р и если

U = 25,9 sin(o / - 11°40') + 6 sin(3 о / + 53°50') В;

i = 3 sin((!> t ~ 40°) +■ 0,9 41 Sin(3 ю t + 125°) A.

Решение.

(Д =25.9/72 = 18,3 В; t/₃ = 6/71 = 4.26 В;

/,=2.1 ЗА: /₃ = 0.9 A;

Ф) =-Н°40'~(-40^э) = 28*40': <p₃ = -71’10';

P = 18,3 ■ 2.13 cos 28’40' + 4.26 • 0.9 cos 7 Г10' = 35.5 Вт;

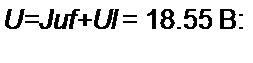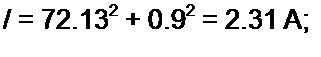5 = V / = 18.55-2.31 = 42.8 BA.

§7.12. Замена несинусоидальных токов и напряжений эквивалентными синусо­идальными. При изучении некоторых простейших свойств нелинейных электрических цепей (см. гл. 15) несинусоидальные токи и напряжения, не содержащие постоянных со­ставляющих и в которых высшие гармоники выражены слабо, заменяют эквивалентными синусоидальными. Действующее значение синусоидального тока принимают равным действующему значению заменяемого песинусоилального тока, а действующее значение синусоидального напряжения — равным действующему значению косинусоидального напряжения.

Сдвиг фаз (р,_к между эквивалентными синусоидами напряжения и тока берут таким, чтобы активная .мощность эквивалентного синусоидального тока была равна акгивной мощности несинусоидальнего тока. т. е.

C0SIK = (7.18)

^э U /

Пример 70. Заменить несинусоидальный ток и напряжение из примера 69 эквивалент­ными и найти сдвиг фаз ср_эк между ними.

Решение. Действующее значение синусоидального напряжения U = 18,55 В; дей­ствующее значение синусоидального тока / = 2,31 A; cos(p_JK = 35,5/(18,55-2,31) = 0,828; Фзх = 34°.