Периодические несинусоидальные токи в линейных электрических цепях

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§ 7.1 Определение периодических несинусоидальных токов и напряжений. Периодическими несинусоидальными токами и напряже­ниями называют токи и напряжения, изменяющиеся во времени по пе­риодическому несинусоидальному закону.

Они возникают при четырех различных режимах работы электричес­ких цепей (и при сочетаниях этих режимов):

1) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а все элементы цепи — резистивные, индуктив­ные и емкостные — линейны, т. е. от тока величины не зависят;

2) если источник ЭДС (источник тока) дает синусоидальную ЭДС (си­нусоидальный ток), но один или несколько элементов цепи нелинейны;

3) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а в состав электрической цепи входят один или несколько нелинейных элементов;

4) если источник ЭДС (тока) дает постоянную или синусоидальную ЭДС (ток), а один или несколько элементов цепи периодически изменя­ются во времени.

В данной главе рассматриваются методика расчета и особеннос­ти работы линейных электрических цепей при воздействии на них несинусоидальных ЭДС и токов — первый из перечисленных режимов работы.

Второй и частично третий режимы работы обсуждаются в гл. 15, чет­вертый — в гл. 18.

§ 7.2 Изображение несинусоидальных токов и напряжений с по­мощью рядов Фурье. Из курса математики известно, что любую перио­дическую функцию Х^') ^с периодом 2 л, удовлетворяющую условиям Дирихле*', можно разложить в ряд Фурье.

Переменная величина х связана со временем t соотношением

2 л

х - (О I - — t,
Т

где Т— период функции во времени.

Таким образом, период функции пох равен 2 л, а период той же функ­ции по времени равен Т.

*’ Вес периодические функции, с которыми имеют дело в электротехнике, условиям Дирихле удовлетворяют. Поэтому производить проверку на выполнение условий Дирихле не требуется.

Ряд Фурье записывают так:

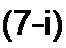/(х) = Ло + sin х + A} sin 2 х + Ay sin 3 х + А\ sin 4 х +...

... + A" cosx + А₂ cos 2 х + Ay cos3 х + cos4 х + ...,

где А$ — постоянная составляющая; А{ — амплитуда синусной (изме­няющейся по закону синуса) составляющей первой гармоники; — амплитуда косинусной составляющей первой гармоники; А'₂ — ампли­туда синусной составляющей второй гармоники и т. д.

Здесь

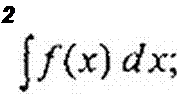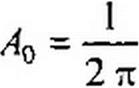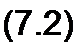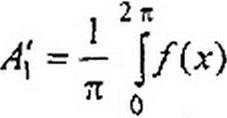
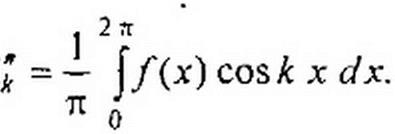
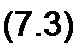
1 ?

A"- — J/(x) cosx с/х;

⁷¹ о

। 2 к

A'_k - — j/(x) sin к х с/х; А
^я о

Так как

А'_к sin к х + А"_к cos А х = А_к sin(к х +- \у_к), где

= yl(A_k)² + (А_к)~ и tg ц/ _к = А_к / А_к,

то ряд Фурье (7.1) можно записать в другой форме:

/(х) = Aq + J, sin(x + y_t) + А₂ sin(2 х + + •••'

= Л_О + £Л* sin(Xr х-ь ч/д-Х

АМ

где А_к — амплитуда Л-гармоники ряда Фурье.

Гармоники, для которых к — нечетное число, называют нечетными¹, для которых к — четное число, — четными.

§ 7.3 Некоторые свойства периодических кривых, обладающих симметрией. На рис. 7.1 изображены три кривые, обладающие некото­рыми специфическими свойствами. Кривая рис. 7.1, а удовлетворяет условию: -/(х + д)= /(х).

Кривые, для которых выполнимо это условие, называют симметрич­ными относительно оси абсцисс. Если кривую рис. 7.1, поместить по оси х на полпериода и зеркально отразить относительно оси х, то получен­ная кривая совпадет с кривой /(х).

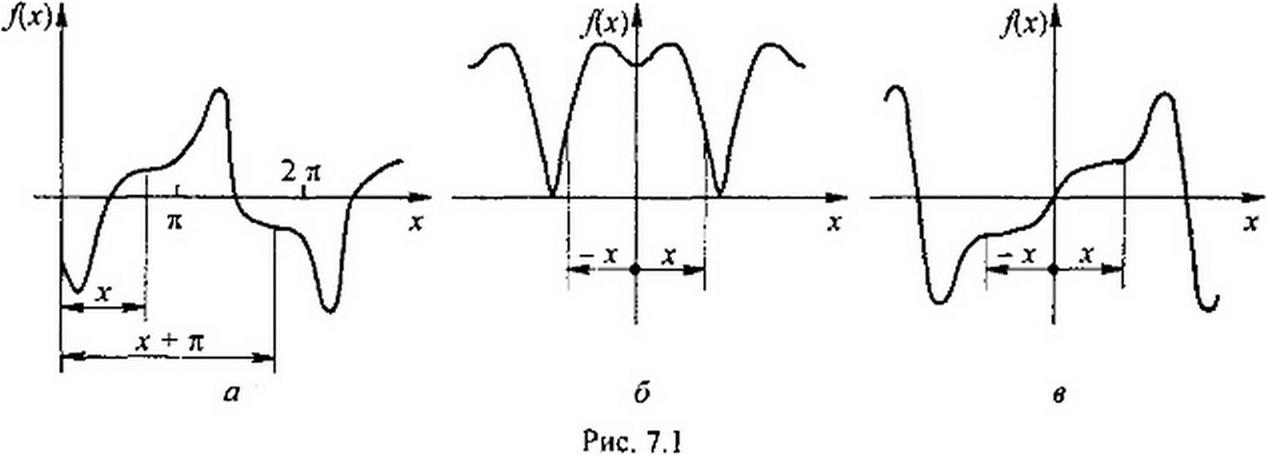
При разложении таких кривых в ряд Фурье отсутствуют постоянная составляющая и четные гармоники, т. е. равны нулю коэффициенты Я_о = Я? = Я^ = Яд = Яд = ... = 0. Поэтому кривые типа кривой на рис. 7.1, а раскладывают в ряд так:

f (х) = Я{ sin х + Я/ cosх + Я₃ sin 3 х + Я₃* cos3 х +....

Каждое слагаемое этого ряда удовлетворяет условию -/(х + л) = /(х), например - sin(x + я) - sin(x).