Ток в нулевом проводе равен нулю, если ток IА> направленный противоположно сумме /л + if по модулю равен 20 V3 А. При этом сопротивление фазы А
£ = £720 Л = 127/20^3 =3,66 Ом.
Пример 61. Определить ток в нулевом проводе схемы на рис. 6.12, а, если в фазу А включить активное сопротивление 3.66 Ом. а индуктивность и емкость фаз 8 и С поме
нять местами: w L = —~ = 6.35 Ом.
о С
Решени е. Векторная диаграмма изображена на рис. 6.13. Из нее следует, что /0 = 34,6 + 34,6 = 69,2 А.
§ 6.9 Соединение нагрузки треугольником. Выберем направление токов в фазах треугольника в соответствии с рис. 6.9, а. Ток IАВ вызывается напряжением UA}i. Модуль и фаза его относительно напряжения (jАЬ определяются сопротивлением нагрузки Zjb.Tok /йс вызван напряжением UKC. Модуль и фаза его относительно 0 определяются сопротивлением Zw-. Ток 1СА вызван напряжением JJCA и зависит от
сопротивления ZCA. Линейные токи вычислим через фазовые токи по пер- вому закону Кирхгофа:
а - 1 ан ~ Ц:а>
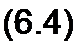 9 9 9
9 9 9
h = I вс ~ АН,
9 9 9
= ^СА ~?НС'
При равномерной нагрузке фаз линейные токи по модулю в 7з раз больше фазовых токов нагрузки. При неравномерной нагрузке линейные токи могут быть и больше и меньше фазовых токов нагрузки.
 |
| ||||
| ||||
Решение. Векторная диаграмма построена на рис. 6.14. б. Напряжения на фазах нагрузки в /з раз больше фазовых ЭДС генератора и равны 220 уЗ = 380 В. Ток iA# опережает напряжение UAf} на 90° и равен 380 / 19 = 20 А. Ток /яг отстает от UH(- на 90° и также равен 20 А. Ток i<-A по модулю равен 20 А и совпадает по фазе с напряжением 0СА. Линейные токи /л> /д, /(< найдем графическим путем, используя соотношения (6.4). По модулю /л /(- - 10 А; /^=20А.
§ 6.10 Оператор а трехфазной системы. Условимся комплексное число е;'20 , по модулю равное единице, обозначать а и называть опе- ротором трехфазной системы. Тогда
л /240* /л;12О\2 2
е = (е' ) = а .
Три вектора — I, а и а2 — образуют симметричную трехфазную систему (рис. 6.15):
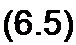 I + а + а2 - 0.
I + а + а2 - 0.
Умножение какого-либо вектора на а поворачивает его без изменения модуля на угол 120° против часовой стрелки. Умножение вектора на а2 поворачивает его на угол 240° против часовой стрелки, или, что то же самое, поворачивает его по часовой стрелке на 120°.
|
С помощью оператора а можно выразить ЭД С £я и Ёс симметричной трехфазной системы через ЭДС £л :
§ 6.11
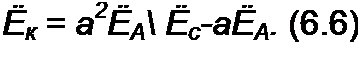 |
Соединение «звезда — звезда без нулевого провода». На рис. 6.8 представлена схема с двумя узлами (точки 0 и О'). Для расчета токов
в ней целесообразно пользоваться методом двух узлов (см. § 2.21). На
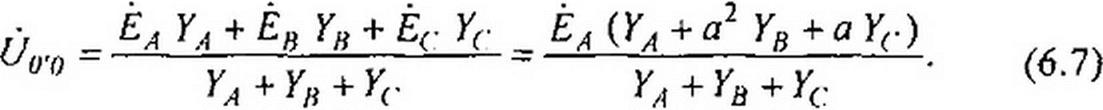 |
пряжение между двумя узлами
Если нагрузка равномерна (YA = = Уг), то (см. соотношение (6.5))
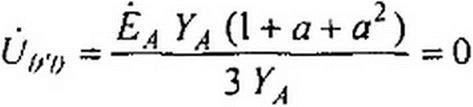 |
и напряжение на каждой фазе нагрузки равно соответствующей ЭДС:
ло' ~ ^во'~^в'-> ^со'-^с
Если нагрузка неравномерна, то О(П) #0 и * • • • • • • • •
АО' = '()'()'■> ВО' = ~U(Hh ^C(i' = ^-( ~^0'()'
Токи в фазах нагрузки;
 |
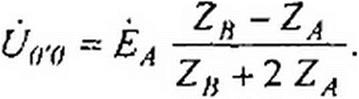 Если в двух фазах нагрузка одинакова, например Z^ ~ZC *ZA, то формула (6.7) после преобразований имеет следующий вид:
Если в двух фазах нагрузка одинакова, например Z^ ~ZC *ZA, то формула (6.7) после преобразований имеет следующий вид:
(6.8)
§ 6.12 Трехфазные цепи при наличии взаимоиндукции. Расчет трехфазный цепей, содержащих магнитно-связанные катушки, осуществляют так же, как и расчет магнитно-связанных цепей однофазного синусоидального тока.
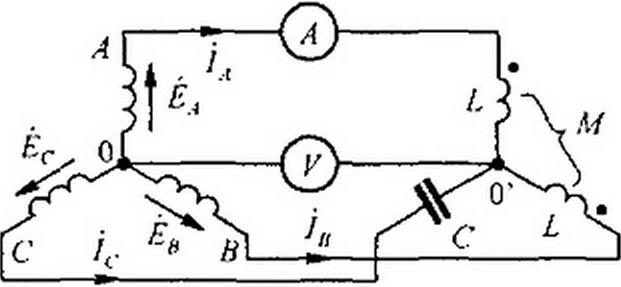
Пример 63. Определить показания амперметра и вольтметра в схеме (рис. 6.16, а). Построить топографическую диаграмму, совместив ее с векторной диаграммой токов. Дано: Еф=127В; со/. = 1/(0С ==4Ом; аМ =2Ом.
Реш ен и е. Выберем положительные направления токов в соответствии с рис. 6.16, а. По первому закону Кирхгофа /А + + /г =0.
 |
|
 |
|
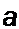 |
Примем ЭДС ЁА, направленной по оси » I. Составим уравнение ио второму закону Кирхгофа для контура ОАО'ВО:
j ю L + 1H j <o M -{1ц J&L + lj j w M) - UAff.
После подстановки числовых значений получим
л./
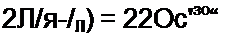 или ^-/^—^=1100-^°° Л.
или ^-/^—^=1100-^°° Л.
Для контура ОСО' ВО
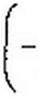 | 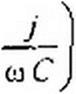 | ||
|
или
~4у/г-2у/я-4У/й=220у.
Совместное решение трех уравнений лает
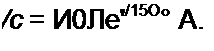 | |||||
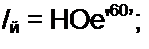 | |||||
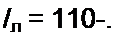 | |||||
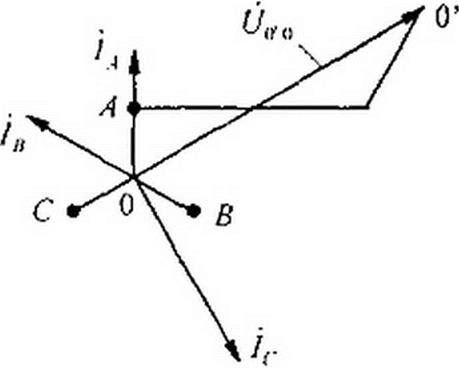
Топографическая диаграмма, соя мешенная с векторной диаграммой токов, изображена на рис. 6 16, б. Амперметр показывает 110 А, вольтметр -— приблизительно 640 В. Последний результат получен после подсчета по формуле
<i>0‘ = Фр + к а ~ j a J « 1'->н J « Л/
§ 6.13 Активная, реактивная и полная мощности трехфазной системы. Под активной мощностью трехфазной системы понимают сумму активных мощностей фаз нагрузки и активной мощности в сопротивлении, включенном в нулевой провод:
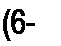 • + Го.
• + Го.
Реактивная мощность трехфазной системы представляет собой сумму реактивных мощностей фаз нагрузки и реактивной мощности в сопротивлении, включенном в нулевой провод:
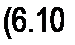 | |||
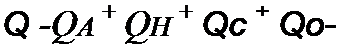 | |||
 | |||||
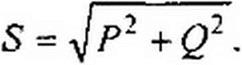 | |||||
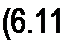 | |||||
Если нагрузка равномерная, то
РА = РВ = РС ^ф 7ф СО5фф;
Qa - Qb - Qc - ^ф s*n Фф’
где фф — угол между напряжением на фазе нагрузки и током /ф фазы нагрузки.
При равномерной нагрузке фаз
^ = 3^ф /ф со5фф;
^ = 3^/ф /ф sin <рф; (6.12)
£ = ЗО'ф /ф.
При равномерной нагрузке фаз независимо от способа ее соединения (звездой или треугольником)
з /ф = Л Л (/ф/ф = Л и,/я, (6.13)
где U„ — линейное напряжение на нагрузке; /л — линейный ток нагрузки.
Поэтому вместо формул (6.12) часто используют следующие:
Р = Л Un /л созфф;
С? = Л(/л /л51Пфф; (6.14)
5 = 7з С/;)
§ 6.14 Измерение активной мощности в трехфазной системе. Для измерения активной мощности трехфазной системы в общем случае (неравномерная нагрузка и наличие нулевого провода) необходимо включить три ваттметра (рис. 6.17). Активная мощность системы равна сумме показаний трех ваттметров. Если нулевой провод отсутствует, то измерение мощности производят двумя ваттметрами (рис. 6.18). Сумма показаний двух ваттметров при этом определяет активную мощность всей системы независимо от того, звездой или треугольником соединена нагрузка (треугольник нагрузки всегда может быть преобразован в эквивалентную звезду).
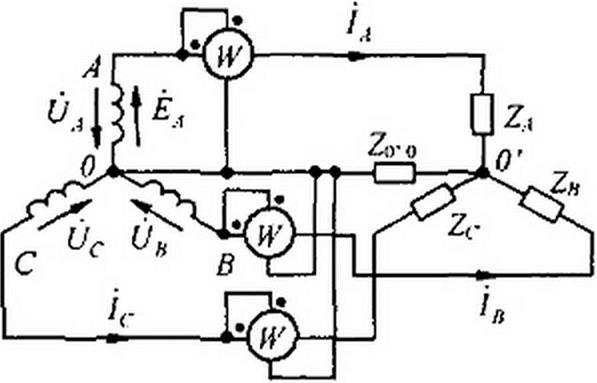 |
|
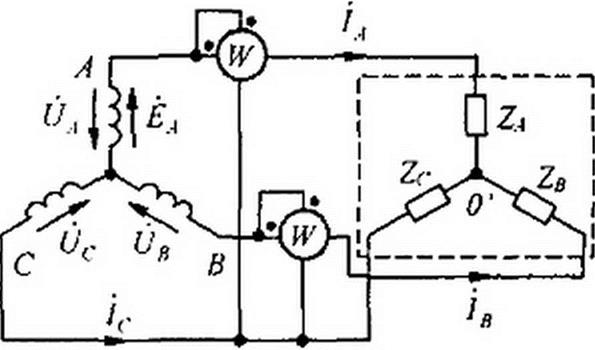 |
|
Показание первого ваттметра равно Ке(7лг /л, второго — Re(7fiC /д, но
Яе(1/лг /\) = Re((^ -Ц-) 1^(0в-йс) =
= Re(l)A !a + Ub h + UcIc\
так как 1А + 1В = -1с.
При равномерной нагрузке фаз достаточно измерить мощность одной фазы и результат утроить.
§ 6.15 Круговые и линейные диаграммы в трехфазных цепях. Если изменяется модуль сопротивления одной из фаз трехфазной цепи, а аргумент его постоянен, то геометрическим местом концов векторов напряжения (тока) любой фазы цепи является окружность или прямая линия.
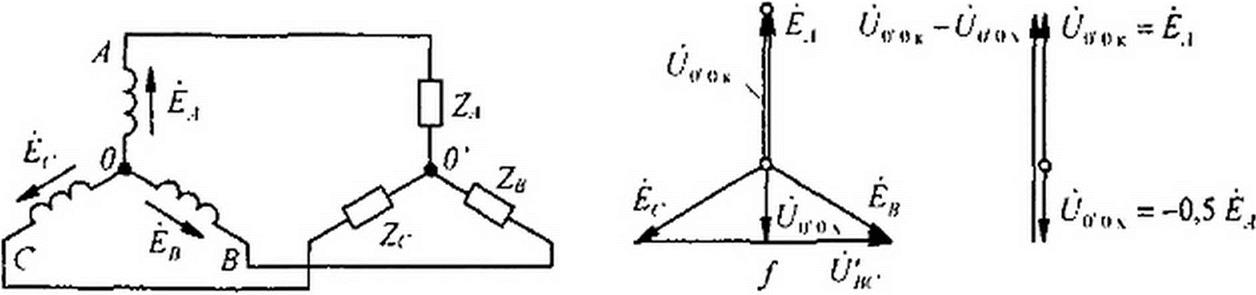
Для примера рассмотрим круговую диаграмму напряжений по схеме (рис. 6.19, а), если ZB ~ZC = г = const и изменяется только модуль сопротивления фазы A(Za).
 |
| ||||
| ||||
Используем формулу (4.80), заменив в ней индексы а и b на О' и 0. В режиме холостого хода ток по фазе А равен нулю, а напряжения на двух сопротивлениях ZB -Z(- =г равны L/^ /2. При этом точка О' находится посередине вектора 0нс (точка f на рис. 6.19, 5); =-0,5 ЁА. При
коротком замыкании сопротивления ZA потенциал точки О' равен потен-
циану точки А. Поэтому = Хордой искомой окружности является разность векторов (рис. 6.19, в) U0>Пк -00'0х = ЁА -(-0,5 Ел) = = 1,5 ЁА. Для определения входного сопротивления ZBX относительно точек А и О’ служит схема на рис. 6.20, а (источники ЭДС закорочены). Два сопротивления г включены параллельно, поэтому ZBX=r/2 и Ч>„ = °'
 | |||||||
 | |||||||
 | |||||||
 | |||||||
Рис. 6.20
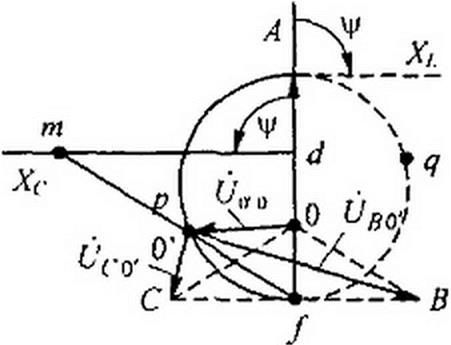
Рассмотрим три случая, отличающихся характером сопротивления Zr ГЕсли ZA— изменяющееся емкостное сопротивление, то Zj --//со С; <рн =-90°; Ф=Ф,(“Фпх --90°. Круговая диаграмма напряжения йП‘о построена на рис. 6.20, б, где линия Хс проведена по отношению к хорде под углом -ф = 90°. Масштаб для Хс соответствует масштабу, в котором отрезок fd выражает входное сопротивление ZBX =г/2. Геометрическим местом точки О' является полуокружность fpA. Для определения модуля и фазы (j()'O при некотором произвольном значении Хс его следует отложить на линии tn d и провести луч fm. Точка пересечения луча /тс полуокружностью fpA обозначена р. Напряжение О(П), соответствующее взятому значению А/, изобразится вектором, проведенным из точки 0 в точку р.
1.1 Если ZA — изменяющееся индуктивное сопротивление, то ф = 90° и геометрическим местом концов вектора Оо-() является полуокружность fqA (штриховая линия на рис. 6.20, б). Линия переменного параметра в этом случае будет справа от точки d.
1.2 Если ZA — чисто активное сопротивление, то ф =фн -фвх = 0° и геометрическим местом концов вектора является прямая Af
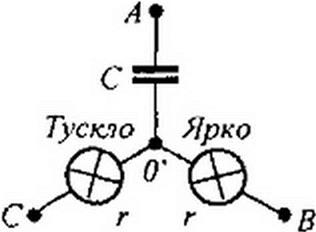
6.16 6.16, Указатель последовательности чередования фаз. Определение последовательности чередования фаз в трехфазной симметричной системе ЭДС (напряжений) осуществляют с помощью указателя последовательности чередования фаз. В простейшем исполнении он состоит из двух одинаковых ламп накаливания и конденсатора (рис. 6.21).
Емкость С выбирают такой, чтобы емкостное сопротивление равнялось резистивному сопротивлению каждой лампы.
Если три конца указателя подключить к трем концам симметричной трехфазной системы ЭДС, то потенциал нулевой точки схемы на рис. 6.21
 |
|
 | |||
 | |||
будет соответствовать положению точки О' на векторной диаграмме рис. 6.20, б.
На диаграмме рис. 6.20, видно, что напряжение на лампах накаливания будет различно. На лампе, включенной в фазу В, оно определяется вектором на лампе, включенной в фазу С, — вектором Так
как то лампа в фазе В будет гореть более ярко, чем лампа в
фазе С. Следовательно, если фазу трехфазной системы ЭДС, к которой подключен конденсатор, принять за фазу А, то фаза, к которой окажется подключенной ярко горящая лампа, есть фаза В, а фаза с тускло горящей лампой — фаза С.
Одним из важнейших свойств многофазных, в частности, трехфазных, токов является их способность создавать круговое вращающееся магнитное поле.
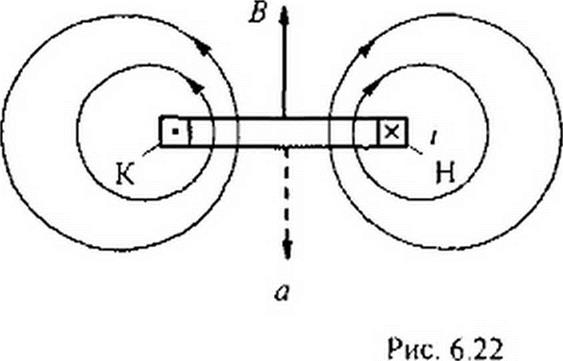
6.17 7. Магнитное поле катушки с синусоидальным током. Магнитное поле одной катушки, по которой протекает синусоидальный ток, представляет собой пульсирующее'’ (не вращающееся) магнитное поле. На рис. 6.22, а изображена катушка, по которой проходит синусоидальный ток / = Im sin о I. Магнитное поле характеризуется вектором магнитной индукции В. Направление В определяется направлением намотки катушки и направлением тока в ней в данный момент времени. Пусть буква Н означает начало, а К — конец катушки. Если ток входит в зажим Н и выходит из зажима К (это направление тока будем считать положительным: ему соответствует интервал времени от 0 до п), то вектор магнитной индукции направлен вверх по осевой линии катушки. В следующий полупериод, когда ток отрицателен, вектор В направлен вниз (штриховая линия на рис. 6.22, о). Таким образом, геометрическим местом концов вектора В является ось катушки.
6.18 8. Получение кругового вращающегося магнитного поля. Круговое вращающееся магнитное поле представляет собой магнитное поле, вектор результирующей магнитной индукции которого имеет постоянное значение и вращается с постоянной угловой скоростью со (см. рис. 6.22, 6).
’•Под пульсирующим полем понимают поле, вектор магнитной индукции которого изменяется (пульсирует) вдоль оси. создающей его катушки с током
а б в
Рис. 6.23
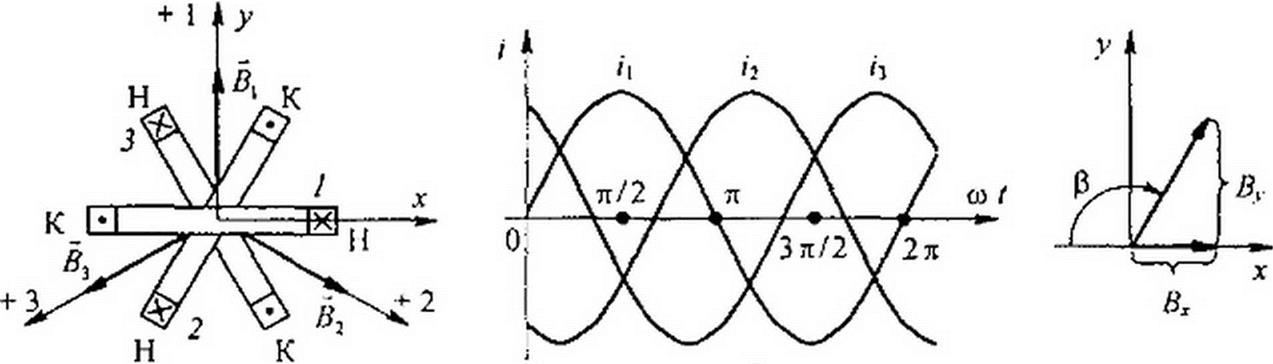
Расположим три одинаковые катушки так, чтобы их оси были смещены на 120° относительно друг друга (рис. 6.23, а). Присоединим катушки к симметричной трехфазной системе ЭДС. Пусть токи входят в начале катушек Н и изменяются следующим образом:
/j = lm sin со /;
/2 = 1 т sin(o) / -120°);
/3 = sin(co / + 120°).
Графики токов изображены на рис. 6.23, б. Каждый из токов создает пульсирующее поле, направленное вдоль оси своей катушки.
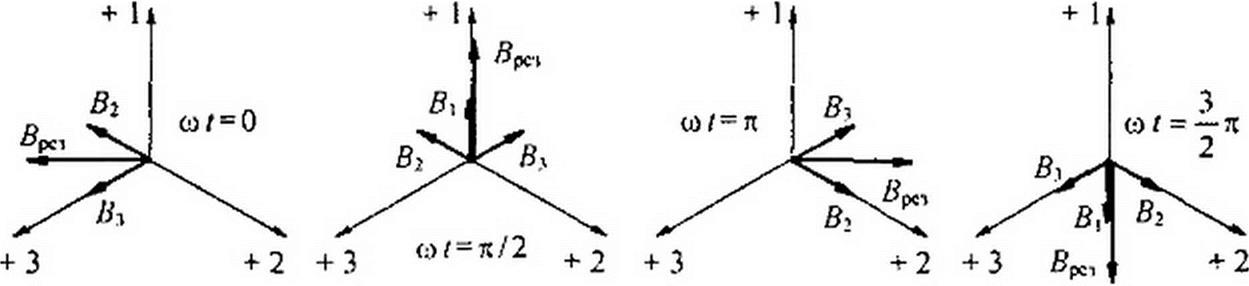
Положительное направление оси первой катушки обозначим + ], второй — +2, третьей — + 3. Магнитную индукцию первой катушки обозначим второй— В1л третьей— В3. Тогда
= Вт sin со Г,
В2 = В,,, sin(co t - 120°);
By = В„, sin(co / + 120°).
Изобразим векторами в пространстве мгновенные значения Вх, В2, By и результирующую индукцию для моментов времени со/ = О, к/2, л, Зл/2 (рис. 6.24, а-г). Запишем алгебраическую сумму проекций векторов магнитных индукций Вь В3 на оси х и у декартовой
а б в
Рис. 6.24
системы координат (см. рис. 6.23, в), совместив ось х с осью 1 и ось у с осью + J:
Вх = В2 cos30° - By cos30° = 1,5 Вп, j\
Ву = Вх- В2 cos 60° - В3 cos 60° - 1,5 Вт.
Мгновенные значения проекций векторов магнитной индукции на оси хну
В = -1,5 Вт cos со /; В = 1,5 Вт sin со Z.
По модулю результирующая индукция В = ^Вх + В? = 1,5 Вт и составляет угол р с осью -х:
tgp = -5v./5r = tgco /,
т. е. угол Р = со t.
С увеличением времени вектор результирующей магнитной индукции, оставаясь по модулю равным 3 Вт /2, вращается с угловой скоростью со по направлению от начала первой катушки с током к началу второй катушки с током Im sin(co / - 120°), т. е. вектор результирующей магнитной индукции вращается в сторону катушки с отстающим током.
Если ток !т sin(co t -120°) пропустить по третьей, а ток Im sin(co t + 120°) — по второй катушке, то направление вращения поля изменится на противоположное.
|
Если произойдет обрыв одной из фаз или ток в ней по амплитуде не будет равен току в какой-либо другой фазе или сдвинут по фазе не на 120°, то образуется эллиптическое вращающееся поле. При его возникновении конец вектора результирующей магнитной индукции будет скользить по эллипсу.
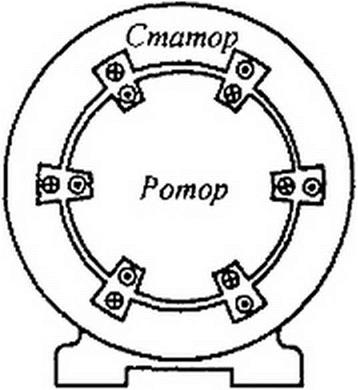
Для того чтобы усилить вращающееся магнитное поле, внутрь катушек помещают полый или сплошной ферромагнитный цилиндр, а стороны катушек заключают в пазы внешнего ферромагнитного цилиндра (рис. 6.25).
Вращающееся магнитное поле используют в электрических двигателях.
Обратим внимание на то, что пульсирующее поле (см. § 6.17) можно представить в виде суммы двух вращающихся в противоположные стороны с угловой скоростью щ магнитных полей. Действительно,
Вт sin со / = (еуш/ - eJ = 0,5 Вт (ея<а'“9°О) + e-'(<tt'-9°O)).
2 j
Вектор 0,5 В„, вращается против часовой стрелки, вектор
0,5 ВП1 е-7(ф/_90’) — по часовой.
§ 6.19 Принцип работы асинхронного двигателя. В промышленности наиболее распространенным типом двигателя переменного тока является трехфазный асинхронный двигатель. В нем имеется неподвижная часть — статор, в пазах которого помешены три катушки, создающие круговое вращающееся магнитное поле, и подвижная часть — ротор, в пазах которого находятся три замкнутые на себя или на внешнее сопротивление катушки. На рис. 6.25 катушки даны в разрезе, их торцовые части не показаны; каждая из катушек занимает лишь небольшую часть окружности статора (или ротора). В действительности каждая из катушек (прямые и обратные провода ее) занимает около 1 / 3 окружности расточки статора (или окружности ротора). Вал ротора двигателя соединен с валом рабочей машины.
Допустим, что сначала ротор неподвижен. При этом вращающееся магнитное поле, созданное обмотками статора, пересекает провода катушек неподвижного ротора с угловой частотой ш и наводит в них ЭДС. В свою очередь, ЭДС вызовут токи в кадушках ротора. По закону Ленца, эти токи стремятся своим магнитным полем ослабить вызвавшее их магнитное поле.
Механическое взаимодействие токов ротора с вращающимся магнитным полем приведет к тому, что ротор начнет вращаться в ту же сторону, в какую вращается магнитное поле (в этом можно убедиться, применив правило левой руки).
В установившемся режиме частота вращения ротора <др составляет (0,98-^0,95) со. Двигатель называют асинхронным потому, что его ротор вращается не синхронно с вращающимся полем; сор не может равняться угловой частоте вращающегося поля. Это станет понятно, если учесть, что при (ор = со вращающееся поле не пересекало бы провода катушек ротора, в них отсутствовал бы ток и ротор не испытывал бы вращающегося момента.
В курсе ТОЭ ограничимся качественным рассмотрением основных положений, характеризующих принцип работы асинхронного двигателя. Подробнее эти вопросы изучают в курсе электрических машин.
§ 6.20 Разложение несимметричной системы на системы прямой, обратной и нулевой последовательностей фаз. Любую несимметричную систему трех токов, напряжений. потоков одинаковой частоты (обозначим их й, Д. С) можно однозначно представить в виде трех систем: нулевой, прямой и обратной последовательностей фаз.
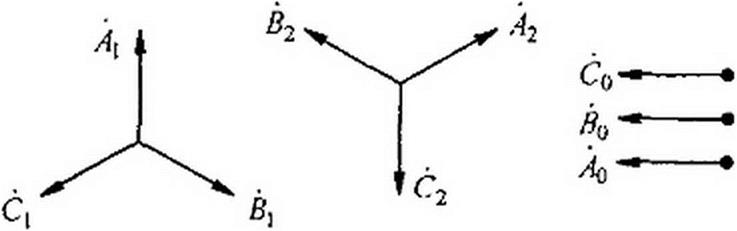
Система прямой последовательности (рис. 6.26, о) состоит из трех векторов — Д;, С], равных по модулю и повернутых относительно друг друга на 120°, причем вектор В} отстает от вектора Д на 120°. Используя оператор а трехфазной системы (см. § 6.10). можно записать:
В]=а2^: С1=аЛ1. (6.15)
Система обратной последовательности (рнс. 6 26. б) состоит из векторов л2> д2, С,, равных по модулю и повернутых относительно друг друга на 120°. причем вектор В2 опережает вектор j2 на 120°:
Д2=аЛ2; С2=й2Я2. (6.16)
| a |
| в |
| б Рис. 6 26 |
| Система нулевой последовательности (рис. 6.26, в) образована тремя векторами, совпадающими по фазе: |
| (6.17) |
| Выразим заданные три вектора А, В, С через векторы симметричных систем следующим образом: |
| А ~ Aq + л, + л2■ В = Bq +■ В\ + Д2; С = Со + С, + С2. |
| (6.18) |
| Перепишем (6.18) с учетом (6.15) и (6.16): |
| Л = Ло + А + ^2 ’ В = Ло + а2 А( +а А2: С = Aq +а А\ + а2 Л2. |
| (6.19) (6.20) (6.21) |
| Из системы уравнений (6.19)-(6.21) найдем Ло. л2. через заданные векторы л, В. С Для определения сложим уравнения (6.19)-(6.21) и учтем, что 1 + а + а2 ~ 0. В результате получим |
| Л0^-(Л + В + С). 3 |
| (6.22) |
| Таким образом, для нахождения Ло следует геометрически сложить три заданных вектора и взять 1 / 3 от полученной суммы. Для нахождения А} к уравнению (6.19) прибавим уравнение (6.20). умноженное на а, и уравнение (6.21), умноженное на а2: |
| Л) =7 (Л+ 4/ ii + a2 С). (6.23) 3 Следовательно. I /3 суммы, состоящей из вектора Л плюс вектор В (повернутый против часовой стрелки на 120°) и плюс вектор С (повернутый по часовой стрелке на 120°), дает вектор Л,. Для вычисления Л2 к уравнению (6.19) прибавим уравнение (6.20), предварительно умноженное на а2, и уравнение (6.21), умноженное на а: |
| Л2 =1(Л + Й2 В + аС). |
| (6.24) |
| § 6.21. Основные положения метода симметричных составляющих. Трехфазные системы передачи электрической энергии состоят из источников энергии, линий передачи. трансформаторов и электродвигателей. В результате какой-либо аварии (например, короткого замыкания или обрыва провода) или при несимметричной нагрузке на элемен- |
 тах системы (электродвигателях, трансформаторах, самой линии передачи) возникают несимметричные напряжения.
тах системы (электродвигателях, трансформаторах, самой линии передачи) возникают несимметричные напряжения.
Расчет токов и напряжений в таких системах производят с помощью схем замещения, на которых все элементы системы должны быть представлены комплексными сопротивлениями. Но сопротивление на фазу одного и того же элемента не одинаково для разных последовательностей. Поэтому расчет следует вести для каждой из последовательностей отдельно, а затем искомую величину (ток или напряжение) определить как сумму токов или соответственно напряжений нулевой, прямой и обратной последовательностей.
Рассмотрим причины, обусловливающие различные значения сопротивления одного и того же элемента для разных последовательностей фаз (при относительно низких частотах).
Сопротивление на фазу трехфазной линии передачи для прямой, обратной и нулевой последовательностей фаз обозначим соответственно 2]л, Z2j), Z<in. Сопротивление на фазу линии передачи для прямой последовательности 21л равно сопротивлению на фазу линии для обратной последовательности Z2n. но не равно сопротивлению на фазу линии для нулевой последовательности фаз вследствие различных значений индукгивности на фазу трехфазной линии для систем прямой и нулевой последовательностей фаз.
Различные значения индуктивностей на фазу линии для прямой и нулевой последовательностей фаз объясняются двумя причинами. Во-первых, индуктивность на фазу линии для прямой и обратной последовагельноетей определяется только геометрическими размерами петель, образованных линейными проводами, тогда как индуктивность на фазу линии для нулевой последовательности зависит не только от геометрических размеров петель, образованных линейными проводами, но и от геометрических размеров петель, образованных линейными проводами и нулевым проводом. Во-вторых, ЭДС. наводимые в петлях провода линии для прямой и обратной последовательностей, представляют собой геометрическую сумму ЭДС. наводимых сдвинутыми по фазе на 120° токами в линейных проводах, тогда как ЭДС, наводимые в петлях проводов линии для нулевой последовательности. созданы совпадающими по фазе токами нулевой последовательности.
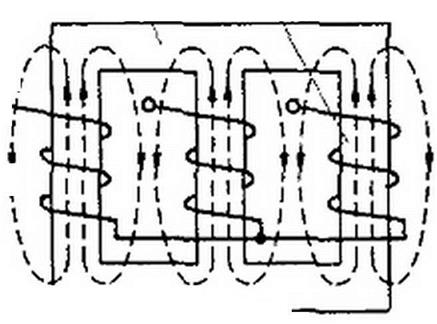
Ярмо Сердечник
Рис. 6 27
В трехфазном трехстержневом трансформаторе (магнитная система его изображена на рис. 6.27) сопротивление на фазу для нулевой последовательности ZOt не равно сопротивлению на фазу для прямой последовательности Z1T, но Z1T = £2г, где Z21 — сопротивление на фазу для обратной последовательности.
Объясняется это главным образом тем. что магнитные потоки нулевой последовательности Фо всех трех фаз находятся в фазе и поэтому нс могут замыкаться по соседним стержням магнитной системы и замыкаются по воздуху (см. рис. 6.27). Магнитные потоки трех фаз прямой Ф, и. соответственно, обратной последовательностей по фазе сдвинуты на 120° и поэтому могут замыкаться по соседним стержням магнитной системы. Так как магнитное сопротивление по пути в воздухе много больше магнитного сопротивления по пути в стали, то при одинаковых токах нулевой и прямой последовательностей Фо < Ф|. Поэтому ZOt<Z1t. Еще большее различие имеют сопротивления прямой Z,„, обратной Z2a и нулевой ZOa последовательностей асинхронного двигателя.
Если к выходным зажимам трехфазного асинхронного двигателя (см. рис. 6.25) одновременно подвести напряжения прямой, нулевой и обратной последовательностей фаз, то
входное сопротивление на фазу двигателя для прямой последовательности Zta не будет равно входному сопротивлению на фазу д,чя обратной последовательности Z2a и оба они будут отличны от входного сопротивления для нулевой последовательности ZQn. Разберем, чем это объясняется.
Пол действием напряжения прямой последовательности в двигателе создается круговое вращающееся магнитное поле. Оно увлекает за собой ротор двигателя. Ротор вращается с угловой частотой с>р. Система напряжений обратной последовательности также создает круговое вращающееся поле, но направление вращения его обратно направлению вращения поля прямой последовательности.
Система напряжений нулевой последовательности вращающегося магнитного поля не создаст. Вокруг статорных обмоток ею создаются пульсирующие потоки, замыкающиеся по воздушному зазору между статором и ротором, подобно тому как в трехстержневом трехфазном трансформаторе (см. рис. 6.27) потоки от нулевой последовательности, выходя из сердечника, замыкались по воздуху.
Входное сопротивление на фазу двигателя для данной последовательности зависит не только от активного и реактивного сопротивлений фазы статорной обмотки, но и от активного и реактивного сопротивлений роторной обмотки (подобно тому как в трансформаторе входное сопротивление определяется не только собственным сопротивлением первичной обмотки, но и сопротивлением, вносимым вторичной обмоткой (см. § 3.39)). Индуктивное сопротивление фазы ротора прямо пропорционально частоте. ЭДС прямой последовательное! н создают в роторе токи частоты (о - <др). что составляет примерно от 0.02 до 0,05о, тогда как токи ротора от обратно вращающегося поля имеют частоту о т (Ор « (1.98^-1,95) о. Так как частоты токов в роторе, создаваемые прямой и обратной последовательностями, различны, то различны и входные сопротивления на фазу для прямой (Zln) и обратной (Z2a) последовательностей.
Магнитные потоки нулевой последовательности фаз замыкаются, минуя ротор, а потоки прямой и обратной последовательностей фаз проходят через ротор. При одном и том же токе прямой и нулевой последовательностей соответствующие им потоки различны. Поэтому для асинхронного двигателя ZOa * Z]a * Z2a.
Расчет до методу симметричных составляющих состоит в следующем. На основании принципа наложения, применимого к линейным цепям, заданный несимметричный режим работы схемы представляют как результат наложения трех симметричных режимов.
В первом симметричном режиме все токи. ЭДС и напряжения содержат только составляющие прямой последовательности фаз. а линии передачи, вращающиеся машины и трехфазные трансформаторы представлены на схемах их сопротивлениями для прямой по сл ело вательности.
Во втором симметричном режиме все токи. ЭДС и напряжения содержат составляющие только обратной последовательности, а машины и трансформаторы представлены их сопротивлениями обратной последовательности.
В третьем симметричном режиме все токи, ЭДС и напряжения содержат только составляющие нулевой последовательности, а машины и трансформаторы представлены соответствующими сопротивлениями нулевой последовательности.
Для того чтобы от симметричной исходной схемы прийти к трем симметричным схемам, поступают следующим образом: в том месте схемы, где создастся несимметрия, в схему вводят сумму трех несимметричных напряжений — 6'4, 0^, 0^-. Система этих напряжений (ЭДС) на основании теоремы компенсации заменяет три неодинаковых сопротивления, образовавшихся в месте аварии и приведших к несим.мстрии во всей схеме. Далее три несимметричных напряжения, в соответствии с § 6.20. раскладывают на три симметричных, основные векторы которых (70. (/;, 02 надлежит определить. Точно так же три несимметричных тока fA> /#. /(- раскладывают на три симметричные системы токов, основные векторы которых /с. /|w /2 следует найти.
В методе симметричных составляющих неизвестными являются шесть величин: три напряжения (6'0. Ц, О2) и три тока (/0, /]% /2), через которые могут быть выражены любые напряжения и токи в цепи.
Для определения шести неизвестных составляют шесть уравнений: по одному уравнению составляют для каждой из трех симметричных систем; остальные три уравнения записывают для того участка схемы, где создается несимметрия. Вид трех последних уравнений зависит от характера несимметрии в схеме.
a
3Zn b 3Z,P
Рис. 6.28
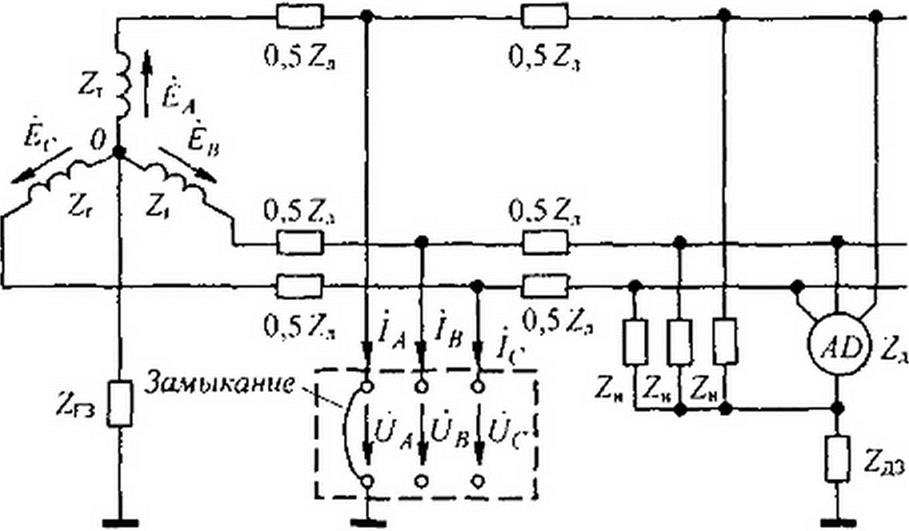
Рассмотрим два примера. Первый пример иллюстрирует расчет при коротком замыкании линейного провода на землю, второй — расчет при разрыве линейного провода. Оба примера приведены для одной и той же схемы до аварии. В первом случае схема изображена на рис. 6.28. а.
Сопротивления на фазу трехфазною генератора ZrI для прямой. обратной и нулевой последовательностей обозначены Z,.}, Zr2. Z^. сопротивления асинхронного двигателя на фазу— Za1. Za2. Za(). сопротивления линии передачи на фазу— Z„t, Z12, Z1Q. Нулевые точки генератора, двигателя, нагрузки заземлены. Сопротивление заземления генератора — 7гЯ. общее сопротивление заземления двигателя и нагрузки обозначено Zn3.
Будем счизагь, что короткое замыкание линейного провода на землю произошло посредине линии, а фазу, к которой эго произошло, назовем фазой А.
Место аварии на рис. 6.28. а окружено штриховой линией в форме прямоугольника. Несимметричные напряжения, образовавшиеся в месте аварии, обозначены О/,
а токи на землю в месте аварии /л< /й, Из рисунка видно, что l)4=0, и /й = /(- = 0. В соответствии с § 6.18 эти три напряжения и три тока представим через их симмегрич-
ные составляющие:
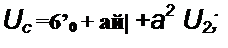 U А — U q + U\ + U2, 0 f) = 0о + а~ U । + a U2,
U А — U q + U\ + U2, 0 f) = 0о + а~ U । + a U2,
^л=А) + А+ ^2> а = о + h + а ! 2» /(• — /о+я/|+а2/2'
Здесь
a = e jr-O\ а 1 =<.}2^
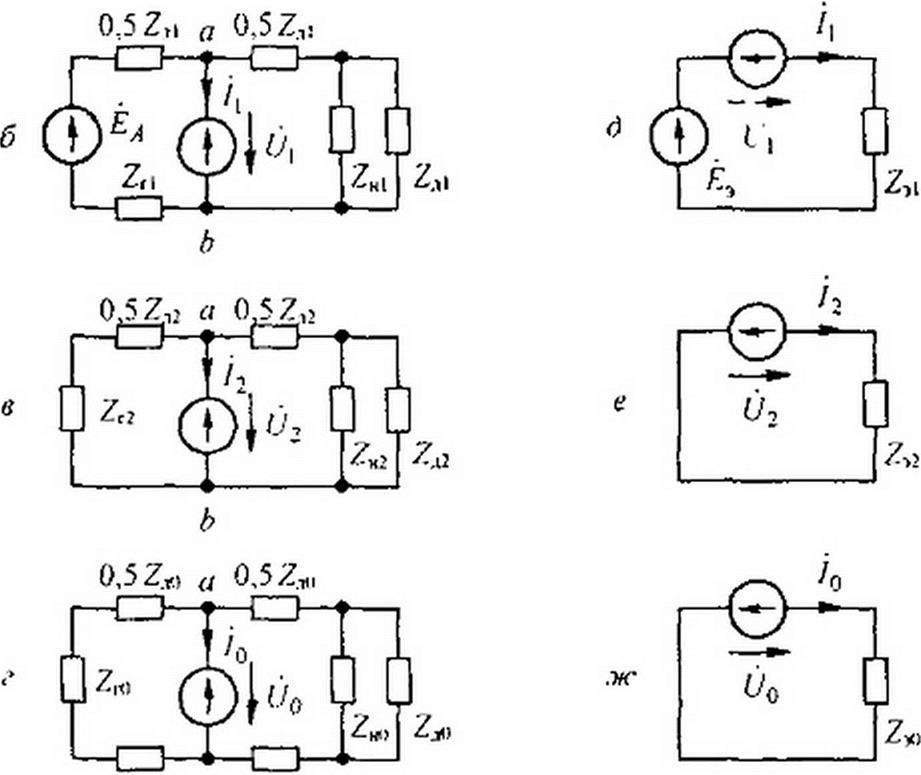
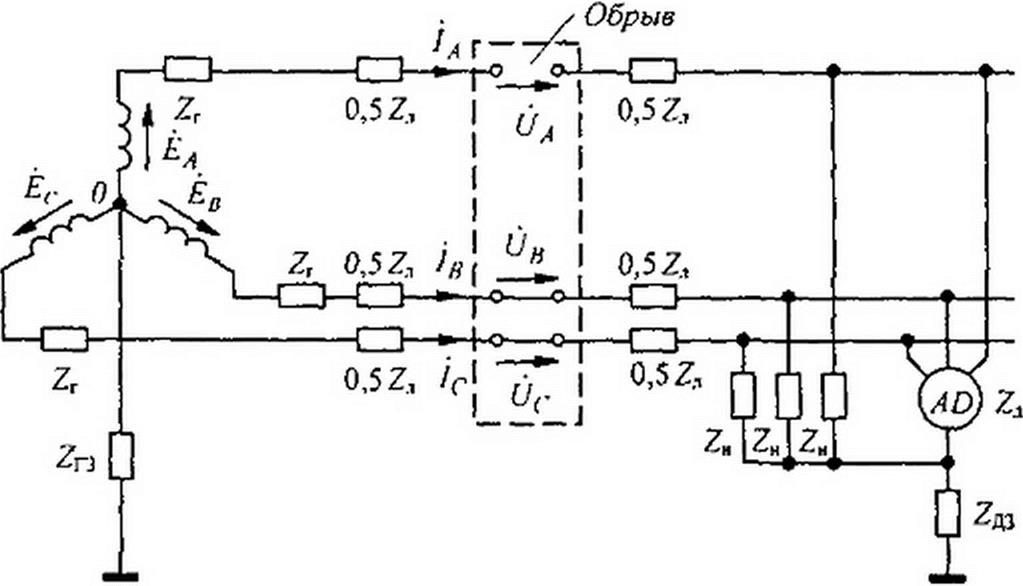
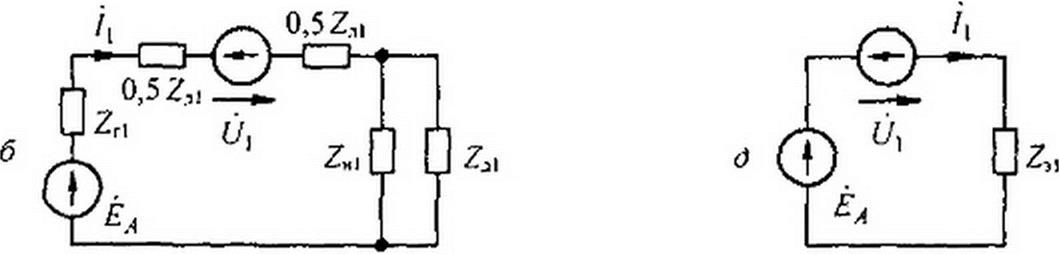
Анализ процессов в несимметричной схеме на рис. 6.28, а методом симметричных составляющих сводится к анализу процессов в трех схемах, изображенных на рис. 6.28, б, в, г. Схема на рис. 6.28, б составлена для токов и напряжений прямой последовательности в фазе А, схема рис. 6.28. в — для обратной последовательности, схема рис. 6.28, г — для нулевой. Так как генератор дает симметричную систему ЭДС прямой последовательности ЁА, Ёв, Ёс (а ЭДС обратной и нулевой последовательностей нс содержит), то ЭДС Еа имеется только в схеме рис. 6.28, б, а в схемах рис. 6.28, в и г ЭДС генератора отсутствует.
Напряжения между точками а и b в этих схемах й}, </2, обозначают напряжения на источниках ЭДС соответственно прямой, обратной и нулевой последовательностей, через которые текут токи /(> /,, /0 этих последовательностей в месте аварии. Все сопротивления в схеме на рис. 6.28.6 имеют дополнительный индекс 1, в схеме рис. 6.28, в — индекс 2, в схеме рис. 6 28. г — индекс 0 или 3.
Утроение сопротивления заземления генератора и двигателя в схеме на рис. 6.28, г для нулевой последовательности объясняется тем, что по нулевому проводу течет ток, в три раза больший, чем по фазовому проводу.
Схемы на рис. 6.28, б. в, г заменяем их эквивалентами на рис. 6 28, б, е, ж, не затрагивая при этом источники ЭДС, напряжение на которых равно (,'ь U-,. 6/0.
Параметры схемы на рис. 6.28, д:
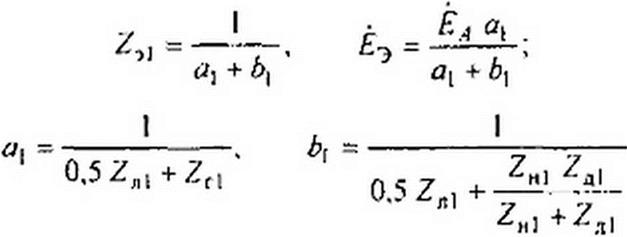 |
Параметры схемы на рис. 6.28, е:
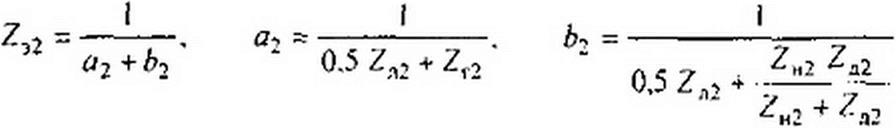 |
Параметры схемы на рис. 6.28, ж:
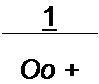 | 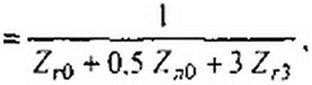 | ||
|
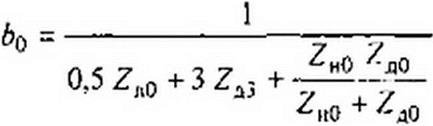 |
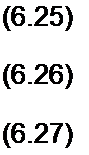
Затем для схем рис. 6.28, б, е, ж составляем уравнения по второму закону Кирхгофа:
Ц +/t Z3i =
(А + /2 Z12 = О-
+ /0 Z,o =0
и дополняем их тремя уравнениями, выражающими через их симметричные составляющие UA> /д. /<•:
 |
|
 | |||||
 | |||||
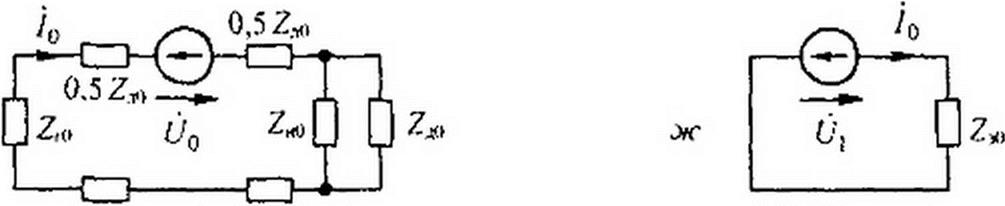 | |||||
|
|
l)A = L'O + U{ + 6'2 =0;
1н - А? +а~ А + й G;
/р = /д + й /| + а~ /j.








