Отношение выходного напряжения четырехполюсника к входному как функция час­тоты о) называют передаточной функцией четырехполюсника. Для схемы рис. 5.12, а К “ ф) /4)5.

Дата: 2025-06-02; Просмотры: 12

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Схема полосно-заграждаюшего фильтра изображена на рис. 5.13, в.

Второе направление реализации активных /?С-фильтров основано на замене обычных индуктивных элементов в к- или фильтр ах на имитированные. При замене учитывают, является ли или может ли быть заземленным один из концов имитируемого индуктивного элемента. Если один из концов заземлен, то выбирают одну схему имитации, если нет, то другую. Так, в схеме фильтра ВЧ (см. рис. 5.2, а) нижний зажим индуктивного элемен­та соединен с землей, т. е. элемент L является заземленным. В схеме фильтра НЧ (см. рис. 5.1, б) ни один из зажимов L не заземлен (т. е. L не заземлена). Поэтому индуктивные элементы в схемах на рис. 5.2, а, 5.1, б должны быть имитированы различно (см. Прило­жение П2).

§ 5.8 Передаточные функции активных ЯС-фильтров в нормированном виде. Будем различать обычную частоту о и нормированную ц>_н, выраженную в долях от частоты среза для НЧ-фильтра (рис. 5.14, а) и в долях от центральной частоты поло-

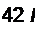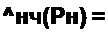
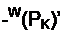
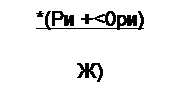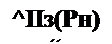Вис. 5.14

сы пропускания (рис 5.14, б) полосно-пропускающсго фильтра. То есть для

НЧФс!)_ч = о/о_с, для ППФ о)_н =со/со_г. Передаточные функции одного звена НЧ-. ПП-, ВЧ- и ПЗ-фильтров в нормированном виде записывают так;

К А,

I' Z \ _ ^Р

*nnW-

Здесь М(р) = р„‘ +т р„ ±п\ = Рн - J «_Рн— нормированная

<7_Р

резонансная угловая частота одного звена фильтра (с>_рн <1). Степень р_н в числителях этих выражений различна. У низкочастотного она нулевая, у ППФ — первая, у ВЧФ и ПЗФ — вторая Уравнение Л/(р_н) = О имеет комплексно-сопряженные корни (полюса К(р_н)). Под добротностью полюсов <?_р одного звена фильтра понимают величину 2а/-/а² + р². Она показывает, насколько острой является частотная характеристика звена (полюса равны -а ± Jp ).

При q < 2 звено фильтра считают низкодобротным, при q_p < 20 — среднедобротным, при q_p > /0 — высокодобротным. Схемы звеньев фильтров с различной величиной Яр приведены в [10].

§ 5.9 Получение передаточной функции низкочастотного активного ЛС-фильт- ра, выбор схемы и определение ее параметров. На рис. 5.14, а изображена зависимость затухания а НЧ-фильтра от частоты св; а_с— частота среза, со,— частота, начиная с которой НЧ-фильтр имеет относительно большое затухание a_min. В полосе пропускания допустимо небольшое затухание а_тах. Порядок расчета — следующий: скачала опреде­лим отношение e>_s/to_c, затем по величинам a_mj)l и a_max по таблицам, помещен­

ным в [10], при выбранном способе аппроксимации частотной характеристики фильтра (см. § 10.12) определяем знаменатель М(р_и) всего фильтра. В таблицах он представлен, как правило, в виде произведения полиномов второго порядка вида р_н² + тр_н + п. Каж­дому полиному соответствует свое звено активного /?С-фильтра. Все звенья соединяют кас- кадио. Для каждого полинома определяем добротность Я_? и по ее величине подбираем схему каждого звена по [10]. После этого передагочную функцию каждого звена денор- мируем, заменяя о_рк на со_р/а>_с. а р_н на уеэ/ш_с. Затем определяем параметры R, С каж­дого звена. С этой целью сопоставляем почленно выражение передаточной функции звена (например, выражения Ф3/Ф5 схемы на рис. 5.12) с полученной функцией К(у<л) звена. Часть параметров в схеме может быть взята произвольно (резисторы — по нескольку' килоом, а конденсаторы — доли микрофарад), другую часть находим из сопоставления. Так как вариантов решения может быть несколько, то выбираем по тем или иным сообра­жениям наиболее целесообразное.

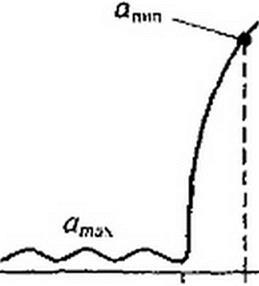
§ 5.10 Получение передаточной функции полосно-пропускающего активного /?С-фильтра. Положим, что требуется получить ПП-фильтр с относительно большим за­туханием о_|П(П в полосах затухания (от о>= 0 до <о_А.| и от o_v2 до ад ) — рис. 5.14, б — и небольшим допустимым затуханием а_тах в полосе пропускания от до a>_w. Цент­ральная частота в полосе пропускания обозначена <о, (в относительных единицах со_г — 1).

Передаточную функцию ПП-фильтра получают на основе частотных преобразований (см. Приложение П6) следующим образом: сначала подсчитывают нормированную часто- О — (Oyj ту W, =—= — НЧ-фильтра прототипа. Затем по и заданным значениям и

^а Л2 ^-°/>1

полосового фильтра, при заданном способе аппроксимации частотной характеристики (по Чебышеву, Баттерворту, Бесселю и т д.) по таблицам, приведенным в [10], определяем нормированную передаточную функцию НЧ-фильгра прототипа. После этого подсчиты- ваем коэффициент Ь = —------------- и в передаточной функции НЧ-фильтра прототипа заме-

У 2 2 ।

5 + О)_г 5 + 1

няем р_и на —------------ — = —------- , т. е. осуществляем переход от НЧ-фильтра к ПП-норми-

Ь 5_И

рованному фильтру (см. Приложение П6).

Здесь 5_И = усо_н, co_ri — текущее значение нормированной угловой частоты. Для пере­хода от нормированной частоты е>_м к ненормированной о заменяем на (о/со_г

Wv KULz М

и со_пн на ------------- .

^₽ е>_г

'ксморм

Обратим внимание на то, что степень полинома знаменателя передаточной функции ПП-филыра увеличивается при этом в два раза по сравнению со степенью полинома зна­менателя передаточной функции НЧ прототипа. Другими словами, каждое квадратичное звено НЧ прототипа заменяется на два каскадно включенных квадратичных звена ПП-филь- тра.

Вопросы для самопроверки

§ 1.1 понимают под электрическими т- и А-фильтрами? 2. Дайте определение поло­сы прозрачности и полосы затухания. Как расчетным путем найти границы полосы про­зрачности для фильтров НЧ и ВЧ, а также полосно-пропускающих и полосно-заграждаю- щих фильтров? 3. Начертите графики изменения Z_c,a и b в функции частоты о для всех известных вам типов фильтров. 4. Из чего следует исходить при выявлении характера Z_c фильтра в полосе затухания? 5. Как по схеме А-фильтра определить, к какому типу он при­надлежит? 6. В че.м недостатки А-фильтров? 7. Как согласовывают полузвенья /«-фильтра с А-фильтром? За счет чего в /«-фильтрах при некоторых частотах возникает бесконечно большое затухание? 8. В чем преимущества т- перед А'-фильтрами? 9. Что послужило ос­нованием подразделять полузвенья /«-фильтров на параллельно-производные и на после­довательно-производные? 10. Чем объяснить, что коэффициент т берут равным 0,55-0,6? II. Чем принципиально отличается /?С-фильтр от А- и /«-фильтров? 12. Что понимают под активными /?С-фильтрами и каковы их достоинства? 13. Какие вы знаете два основных направления реализации активных /?С-фильтров? 14, Какие способы создания имитиро­ванной индуктивности вы знаете'’ 15. Выведите формулы зависимости затухания а от ча­стоты о; а) для фильтра на рис. 5.12, а: б) для фильтра на рис. 5.13, б; в) для фильтра на рис. 5.13, в. 16. Решите задачи 14.1; 14.4; 14.6; 14.7; 14.18; 14.21; 14.22.

Глава шестая

ТРЕХФАЗНЫЕ ЦЕПИ

§ 1.2 Трехфазная система ЭДС. Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС оди­наковой частоты и амплитуды, сдвинутых по фазе на 120°. Графики их мгновенных значений изображены на рис. 6.1, векторная диаграмма — на рис. 6.2. Принцип получения трехфазной системы ЭДС иллюстрирует рис. 6.3. В равномерном магнитном поле с постоянной угловой скорос­тью со вращаются три одинаковые жестко скрепленные друг с другом катушки.

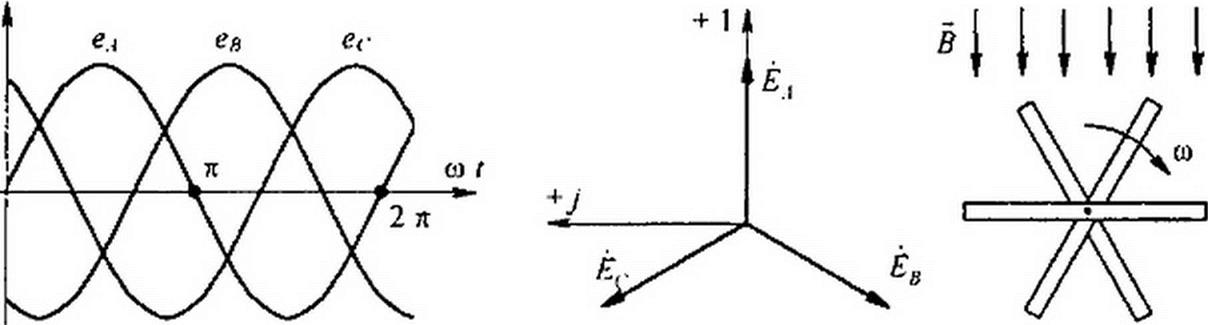
Рис. 6.1 Рис. 6.2 Рис. 6.3

Плоскости катушек смещены в пространстве друг относительно дру­га на 120°. В каждой катушке наводится синусоидальная ЭДС одинако­вой амплитуды. По фазе ЭДС катушек сдвинуты на 120°.

Аналогичным путем можно получить двух- и четырехфазную систе­му ЭДС и более фазную. Наибольшее практическое применение получи­ла трехфазная система.

ЭДС трехфазного генератора обозначают следующим образом: одну из ЭДС — Ё_А, отстающую от нее на 120° ЭДС — E_lf, а опережающую на 120° — Ё_с.

Последовательность прохождения ЭДС через одинаковые значения (например, через нулевое значение) называют последовательностью фаз.

§ 1.3 Принцип работы трехфазного машинного генератора.

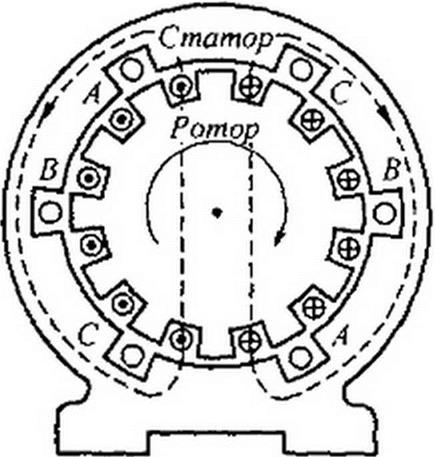
В машинном генераторе (рис. 6.4) обмотки неподвижны (помещены в пазы статора); на рисунке они обозначены буквами А, В, С. Магнитное поле в генераторе создается вращающимся ротором с намотанной на него катушкой, по которой протекает постоянный ток. Если число пар полю­сов ротора равно единице, то угловая частота вращения ротора равна уг­ловой частоте вращающегося магнитного поля. Магнитная цепь в такой конструкции почти замкнута (имеется только небольшой зазор между статором и ротором), что позволяет получить значительный поток при

относительно небольшой магнитодвижущей силе обмотки ротора. При конструировании генератора стремятся к тому, чтобы распре­деление магнитной индукции по окружнос­ти статора было практически синусоидально. На рис. 6.4 штриховыми линиями показаны магнитные силовые линии в некоторый мо­мент времени.

§ 1.4 Трехфазная цепь. Расширение по­

нятия фазы. Совокупность трехфазной сис­

темы ЭДС, трехфазной нагрузки (нагрузок) и

соединительных проводов называют трех­фазной цепью.

Токи, протекающие по отдельным участкам трехфазных цепей, сдви­нуты относительно друг друга по фазе. Под фазой трехфазной цепи по­нимают участок трехфазной цепи, по которому протекает одинаковый ток. В литературе фазой иногда называют однофазную цепь, входящую в со­став многофазной цепи. Под фазой будем также понимать аргумент си­нусоидально меняющейся величины. Таким образом, в зависимости от рассматриваемого вопроса фаза — это либо участок трехфазной цепи, либо аргумент синусоидально изменяющейся величины.

§ 1.5 Основные схемы соединения трехфазных цепей, определе­ние линейных и фазовых величин. Существуют различные способы соединения обмоток генератора с нагрузкой. Самым неэкономичным спо­собом явилось бы соединение каждой обмотки генератора с нагрузкой двумя проводами, на что потребовалось бы шесть соединительных про­водов. В целях экономии обмотки трехфазного генератора соединяют в звезду или треугольник. При этом число соединительных проводов от генератора к нагрузке уменьшается с шести до трех или до четырех.

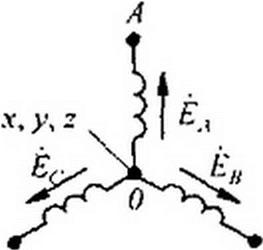
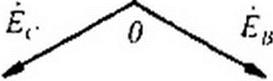
На электрической схеме трехфазный генератор принято изображать в виде трех обмоток, расположенных друг к другу под углом 120°. При соединении звездой одноименные зажимы (например, концы х_уу, z) трех обмоток объединяют в одну точку (рис. 6.5), которую называют нулевой точкой генератора 0. Обмотки генератора обозначают буквами А, В, С; буквы ставят: А — у начала первой, В — у начала второй и С — у начала третьей фазы.

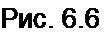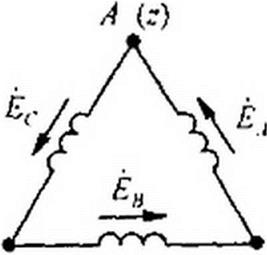
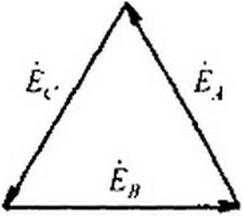
При соединении обмоток генератора треугольником (рис. 6.6) конец первой обмотки генератора соединяют с началом второй, конец вто­рой — с началом третьей, конец третьей — с началом первой. Геометри­ческая сумма ЭДС в замкнутом треугольнике равна нулю. Поэтому если к зажимам Л, 5, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток.

Обратим внимание на то, что расположение звезды или треугольника векторов фазовых ЭДС на комплексной плоскости не следует связывать с расположением в пространстве осей трех обмоток генератора.

Пять простейших способов соединения трехфазного генератора с трехфазной нагрузкой изображены на рис. 6.7-6.10.

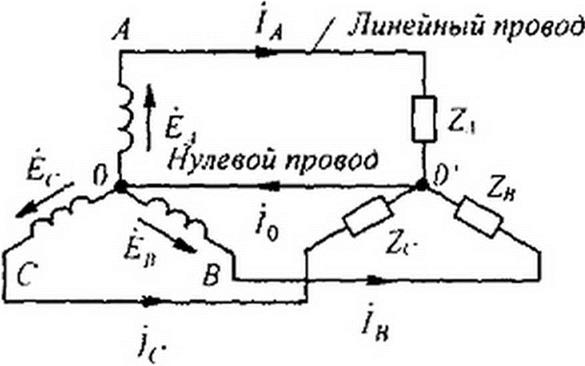
Точку, в которой объединены три конца трехфазной нагрузки при соединении ее звездой, называют нулевой точкой нагрузки и обознача­ют О'. Нулевым проводом называют провод, соединяющий нулевые точ­ки генератора и нагрузки. Ток нулевого провода назовем /₀. Положитель­ное направление тока возьмем от точки О' к точке 0.

Провода, соединяющие точки А, В, С генератора с нагрузкой, назы­вают линейными.

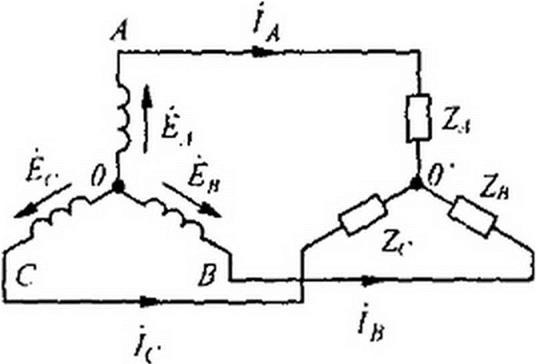
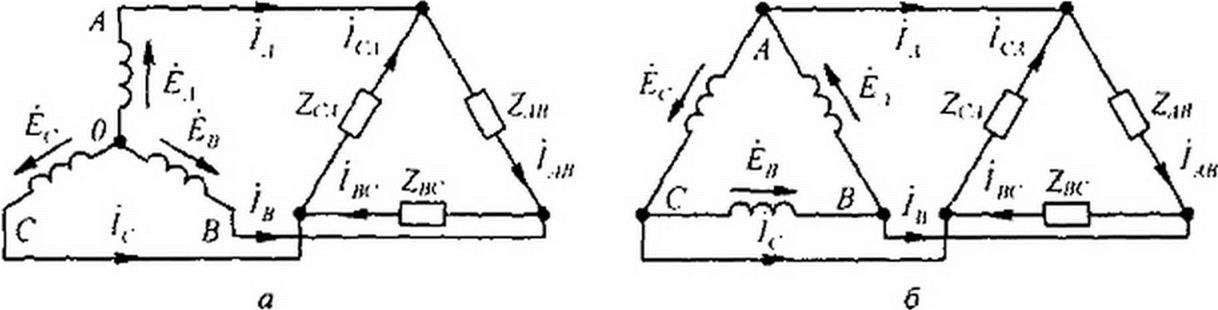
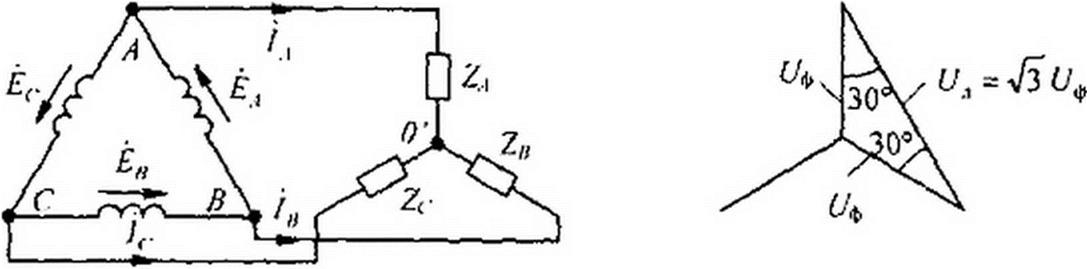
Схему на рис. 6.7 называют «звезда — звезда с нулевым проводом»; на рис. 6.8 — «звезда — звезда без нулевого провода»; на рис. 6.9, а — «звезда — треугольник»; на рис. 6.9, б — «треугольник — треугольник»; на рис. 6.10 — «треугольник — звезда».

Текущие по линейным проводам токи называют линейными', их обо­значают 1_А> /_Л, 1_С. Условимся за положительное направление токов принимать направление от генератора к нагрузке. Модули линейных то­ков часто обозначают /_л (не указав никакого дополнительного индекса), особенно тогда, когда все линейные токи по модулю одинаковы.

Напряжение между линейными проводами называют линейным и часто снабжают двумя индексами, например (j _АН (линейное напря­жение между точками А и 5); модуль линейного напряжения обозна­чают U_n.

Каждую из трех обмоток генератора называют фазой генератора; каж­дую из трех нагрузок — фазой нагрузки; протекающие по ним токи — фазовыми токами генератора /_ф или, соответственно, нагрузки, а напря­жения на них — фазовыми напряжениями (^ф)-

§ 1.6 Соотношения между линейными и фазовыми напряжения­ми и токами. При соединении генератора в звезду (см. рис. 6.7; 6.8; 6.9, а) линейное напряжение по модулю в 7з раз больше фазового напряжения генератора ((7_ф). Это следует из того, что есть основание равнобедренного треугольника с острыми углами по 30° (рис. 6.11):

= ^ав = 2 cos30° = л/з £/_ф. (6.1)

В основу формирования ряда трехфазных напряжений, когда после­дующее напряжение больше предыдущего в 7з раз, положен д/з = 1,73. Приведем часть этого ряда при относительно низких напряжениях: 127, 220, 380, 660 В.

Линейный ток /_л при соединении генератора в звезду равен фазово­му току генератора: /_л - /_ф.

При соединении генератора в треугольник линейное напряжение равно фазовому напряжению генератора (см. рис. 6.6; 6.9, б):

(6.2)

При соединении нагрузки в звезду (см. рис. 6.7; 6.8; 6.10) линейный ток равен фазовому току нагрузки: /_л = /_ф.

При соединении нагрузки треугольником положительные направления для токов выбирают по часовой стрелке. Индексы у токов соответствуют выбранным для них положительным направлениям: первый индекс от­вечает точке, от которой ток утекает, второй — точке, к которой ток при­текает.

При соединении нагрузки треугольником (см. рис. 6.9, а, б) линейные токи не равны фазовым токам нагрузки и определяются через них по первому закону Кирхгофа:

Iа ~ АН " Ё'А> W • %

h - he ~ ¹АН'

♦ г •

Ё' - Ё'А ~ he-

§ 6.6 Преимущества трехфазных систем. Широкое распростране­ние трехфазных систем объясняется главным образом тремя основными причинами:

1) передача энергии на дальние расстояния трехфазным током эконо­мически более выгодна, чем переменным током с иным числом фаз;

2) элементы системы — трехфазный синхронный генератор, трехфаз­ный асинхронный двигатель и трехфазный трансформатор — просты в производстве, экономичны и надежны в работе;

3) система обладает свойствами неизменности значения мгновенной мощности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.

§ 6.7 Расчет трехфазных цепей. Трехфазные цепи являются разно­видностью цепей синусоидального тока, и потому расчет и исследование процессов в них производят теми же методами и приемами, которые рас­сматривались в гл. 3 и 4. Для цепей трехфазного тока применим также символический метод расчета и можно строить векторные, топографи­ческие и круговые диаграммы.

Аналитический расчет трехфазных цепей рекомендуется сопровождать построением векторных и топографических диаграмм. Векторные диаг­раммы облегчают нахождение углов между токами и напряжениями, де­лают все соотношения более наглядными и помогают находить ошибки при аналитическом расчете, если последние возникнут.

§ 6.8 Соединение «звезда — звезда с нулевым проводом». Если ну­левой провод в схеме (см. рис. 6.7) обладает весьма малым сопротивле­нием, то потенциал точки О' практически равен потенциалу точки 0\ точки О' и 0 фактически представляют собой одну точку. При этом в схеме образуются три обособленных контура, через которые проходят токи — Ё _А — Ё_и /[ <• — Ё(' /

По первому закону Кирхгофа ток в нулевом проводе равен геометри­ческой сумме фазовых токов:

/₀ = /_л + /_й + /_с. (6.3)

Если Z_A - Z_c (такую нагрузку называют равномерной), то ток /₀ равен нулю и нулевой провод может быть изъят из схемы без изме­нения режима ее работы.

При неравномерной нагрузке фаз ток /₀ в общем случае не равен нулю.

При наличии в нулевом проводе некоторого сопротивления расчет схемы производят методом узловых потенциалов.

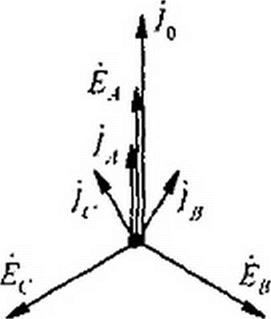
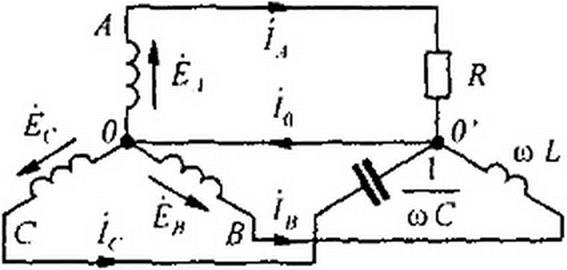
Пример 59. В схеме (рис. 6.12, а) ЭДС каждой фазы трехфазного генератора равна 127 В. Сопротивления фаз нагрузки равны по модулю (6,35 Ом), но имеют различный характер: Z _А = Я, 2_Й = jе L, Z₍- = -J/aC. Определить ток а нулевом проводе.

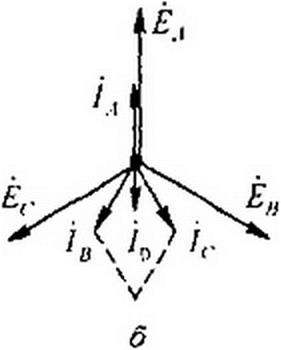
Решение. Построим векторную диаграмму (рис. 6.12, о). Токи всех фаз по моду­лю равны 127/6.35 = 20 А. Ток f_A совпадает по фазе с Е_А. Ток на 90° отстает от £_Л. Ток /(• опережает £₍> на 90°. Сумма 1_А+1_н + 1с даст вектор тока /₀. По модулю он равен 14,6 А.

Пример 60. Какое значение должно иметь сопротивление в фазе А схемы (см. рис. 6.12, о). чтобы ток в нулевом проводе стал равным нулю?

Решение. Геометрическая сумма токов /# ч- по модулю равна

2-20cos30° = 20 Л А.