Для П-фильтра ВЧ (см. рис. 5.2, б) Zcn -

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Z_c)! = /(to) представлен на рис. 5.2, д.

Если фильтр предназначен для работы на частотах, находящихся внут­ри полосы прозрачности данного фильтра и относительно далеко отсто­ящих от значения со, при котором Z_c = 0, то сопротивление нагрузки Z_H на выходе фильтров НЧ выбирают равным Z_c, которое соответствует to - <0t = 0. Для Т-фильтра НЧ (см. рис. 5.1, a) Z_c = у/2 L/C.

Для фильтров ВЧ обычно нагрузку согласовывают со значением Z_c при to ->оо. Для Т-фильтра ВЧ (см. рис. 5.2, a) Z_cT = ^2 L/C. В полосе (полосах) затухания Z_c оказывается чисто реактивным для всех типов ^-фильтров.

Для того чтобы выяснить, индуктивный или емкостный характер име­ет Z_c в полосе затухания, следует определить характер входного сопро­тивления этого фильтра (фильтр всегда работает в режиме согласован­ной нагрузки) для предельного режима, а именно для фильтров НЧ (см. рис. 5.1, а, б) при очень высокой частоте, а для фильтров ВЧ (см. рис. 5.2, а, б) при очень низкой частоте (теоретически при to —> 0), считая выходные зажимы схем закороченными. Тот же результат будет получен, если считать их разомкнутыми. В результате определим, что в зоне затухания Z_c имеет индуктивный характер для Т-фильтра НЧ (см. рис. 5.1, а) и П-фильтра ВЧ (см. рис. 5.2, б) и емкостный характер для П-фильтра НЧ (см. рис. 5.1, б) и Т-фильтра ВЧ (см. рис. 5.2, а).

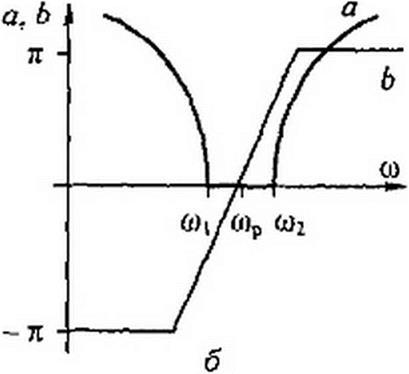
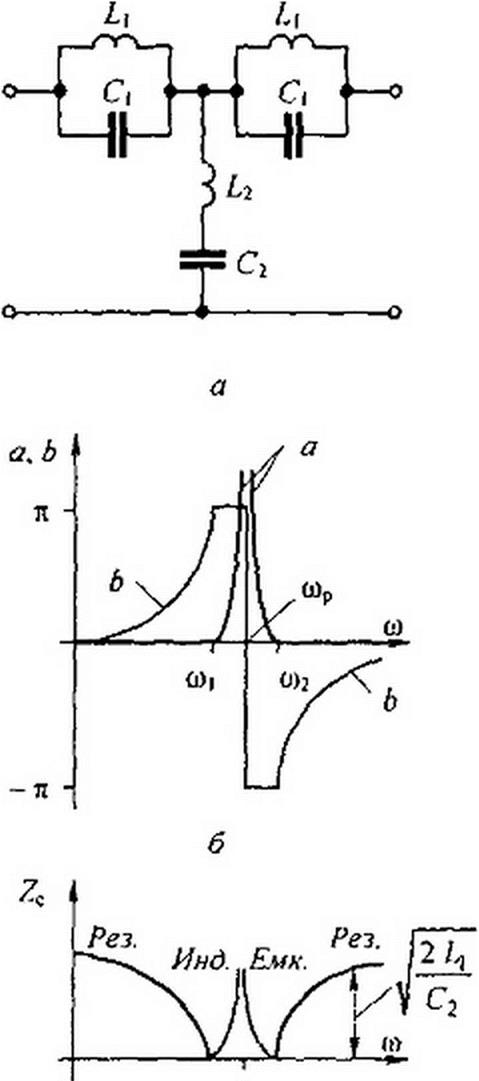
Полосно-пропускающие фильтры представляют собой фильтры, про­пускающие в нагрузку лишь узкую полосу частот от to₍ до to₂. Слева от toj и справа от <о₂ находятся полосы затухания. Схема простейшего по- лосно-пропускающего ^-фильтра изображена на рис. 5.3, а. Параметры схемы должны удовлетворять условию L\ С| = L₂ С₂.

Характер изменения а и b для полосно-пропускаюшего фильтра ил­люстрируют кривые рис. 5.3, б.

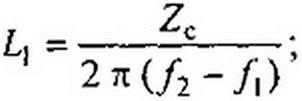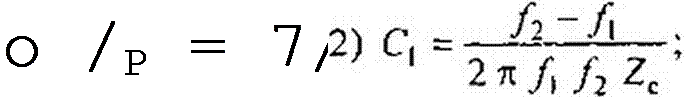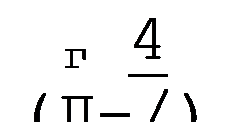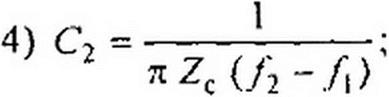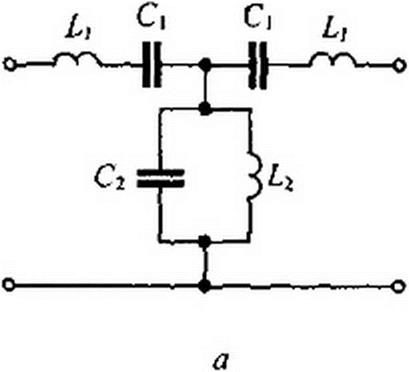
Без вывода дадим формулы для определения параметров фильтра рис. 5.3, а по заданным частотам / и /₂ и сопротивлению нагрузки фильтра Z_c при резонансной частоте /_р =со_р/2тг:

Под полосно-заграждающими фильтрами (рис. 5.4, я) понимают фильтры, в которых полоса прозрачности как бы разрезана на две части полосой затухания (рис. 5.4, б). Слева от и справа от <о₂ находятся две части полосы прозрачности.

В схеме простейшего заграждающего фильтра на рис. 5.4, а

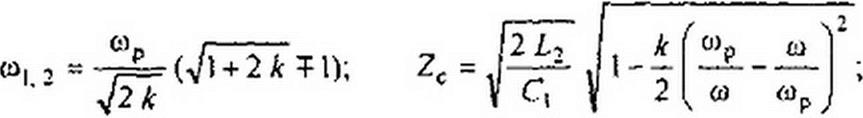для рис. 5.4, а

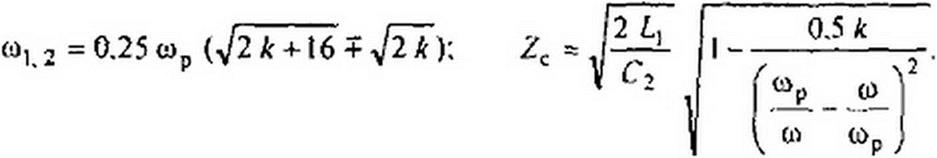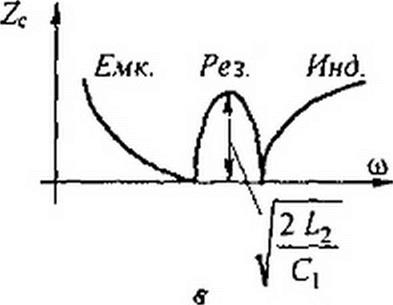
Для фильтра рис. 5.3, а в области частот от 0 до ец Z_c имеет емкостный характер, а в области частот от w₂ до <х> — индуктивный. Для фильтра рис. 5.4, а в области частот от о); до Z_c имеет индуктивный характер, а в области от <л_р до о)₂ — емкостный.

Характер изменения Z_c иллюстрируют кривые на рис. 5.3, в и 5.4, в.

Пример 57. В схеме рис. 5.5, a L = 10 мГн; С = 10 мкФ. Определить b - f (со) и а = /(со) в полосе затухания. Построить векторную диаграмму при со = 2000 рад/с и токе /₂ = 0.2 А при согласованной нагрузке. Вывести формулу расчета фильтра (рис. 5.5, а) при работе его в несогласованном режиме.

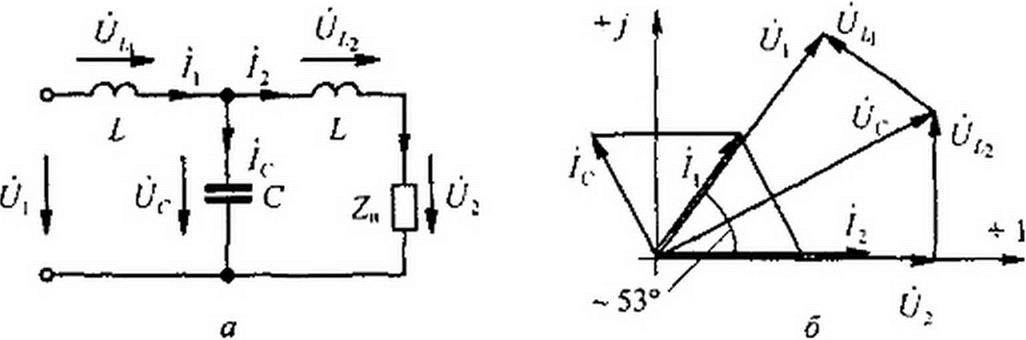
Рис. 5.5

Решение. Частота среза со₂ =■- J—— = 4470 рад/с В полосе пропускания а = 0, у Z. С ।

b = агссозЛ = агссо$(1 — со² Л С). При ы - 2000 рад/с. b - 53°15‘, о L = 20, ------------------------------------------------------------------------------- — 50 Ом,

о С

12 L

Z_H - Z_c = J----------- o>²Z?=40Om. Векторная диаграмма изображена на рис. 5.5, б;

I

02 = A Z„ = 8 В, I/. = U₂ a¹¹ c^jh -0₂ е ^/53°¹⁵ В. В полосе затухания при согласованной нагрузке а= Arch (со* LC-1). Нели Z,, будет не согласована с Z_c, то расчет фильтра в полосе пропускания и в полосе затухания можно проводить, используя соотношения

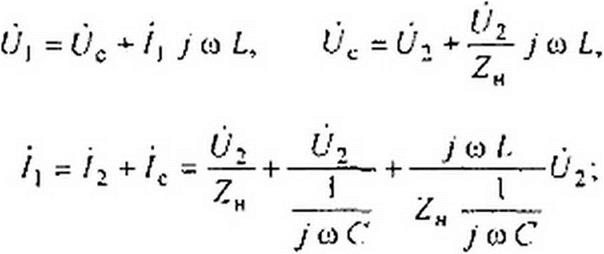
б'] = т 0₂.

где

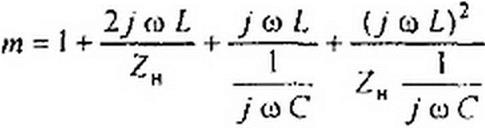
Если взять о = 2 о)2 ~ 8940 рад/с (работа в полосе затухания) и Z_K = 40 Ом (вместо /77,5 0м, исходя из условия согласованности), то от = 13.37 е^{7 50} . те. затухание будет In (Ui/IJ₂} = In 13,37 = 2,59 Hu (вместо 2,53 при согласованной нагрузке).

Аналогичные формулы для несогласованного режима можно вывести для любого дру­гого фильтра.

Пример 58. Определить параметры полосового фильтра рис. 5.3, а. исходя из того, что он должен пропускать полосу частот от / = 750 Гц до /₂ = 850 Гц и что при резо­нансной частоте /_р сопротивление нагрузки Z_K = Z_c - И30 О.м.

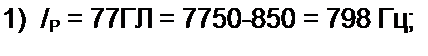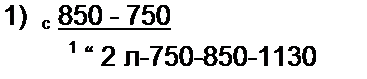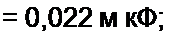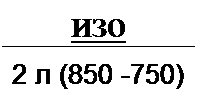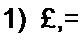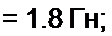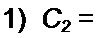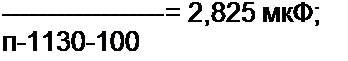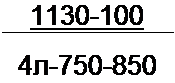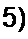§ 5.4 Качественное определение А-фильтра. По схеме А-фильтра без проведения подробного математического анализа можно судить о том, к какому из перечисленных типов может быть отнесен тот или иной фильтр. Заключение основывается на характере продольного сопротивления фильтра.

Характер продольного сопротивления А-фильтра, как правило, прямо противоположен характеру поперечного сопротивления. В этом можно убедиться, рассмотрев схемы на рис. 5.1, а, 5.2, а и 5.3, а. Действитель­но, если продольное сопротивление индуктивное, то поперечное — ем­костное. Если продольное сопротивление образовано последовательно соединенными £ и С, то поперечное — параллельно соединенными L и С и т. д. Если продольное сопротивление состоит только из индуктивно­стей, то фильтр относится к категории НЧ; если продольное сопротив­ление чисто емкостное, то фильтр — ВЧ.

Если продольное сопротивление состоит из последовательно соединенных L и С, то фильтр полосового типа. Если продольное сопро­тивление состоит из параллельно соединенных L и С, то фильтр — за­граждающего типа.

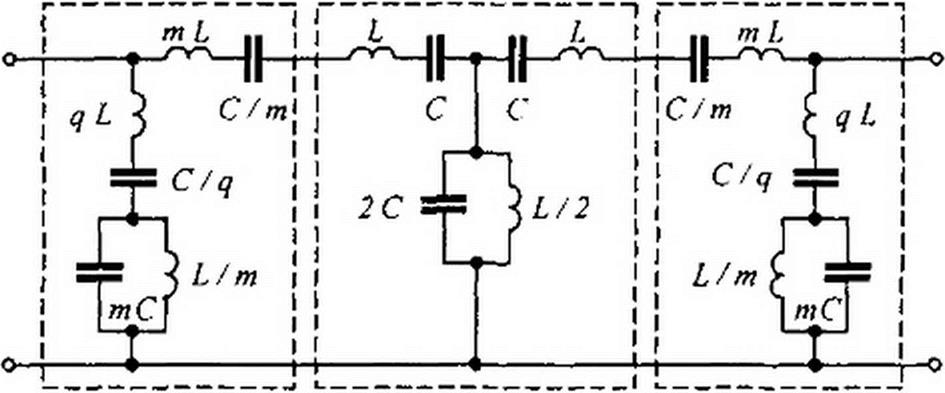
§ 5.5 Основы теории m-фильтроа. Каскадное включение фильтров. Для увеличе­ния крутизны характеристики а = /(о) в начале полосы затухания, получения заданного значения затухания при определенной частоте (частотах) и меньшей зависимости Z_c от частоты в полосе прозрачности применяют полузвенья «-фильтров. каскадно включаемые с А-фильтрами.

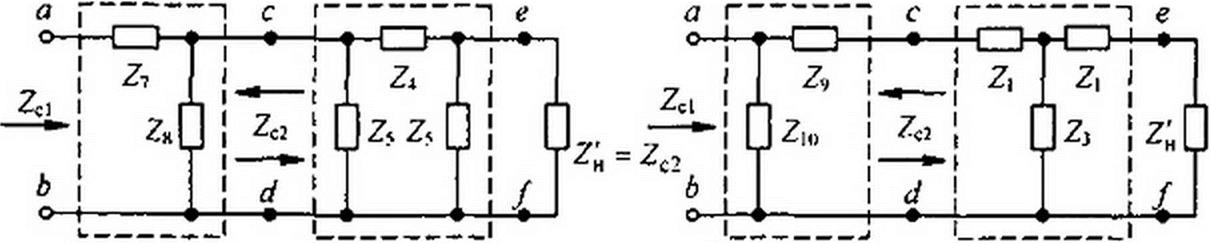
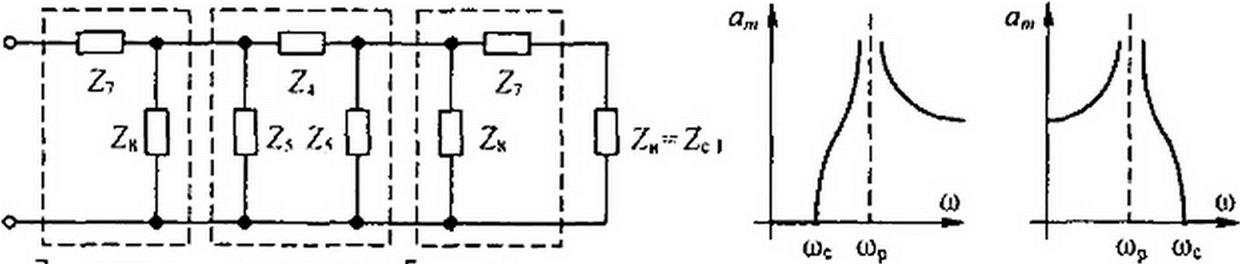
На рис. 5.6 в качестве примера изображены две возможные схемы каскадного вклю­чения “|-полузвсна т- и /с-фильтров. На практике обычно применяют также схемы, в кото­рых ^-фильтр находится между двумя полузвеньями «-фильтра.

		Рис. 5.6

Входное сопротивление фильтра Z_C1 берут равным сопротивлению источника сигнала (источника питания) Z„. Схемы, приведенные на рис. 5.6, применяют, когда сопротивление нагрузки на выходе фильтра Z„ не может быть взято равным Z_K. Схему на рис. 5.8, а и ей подобные используют, когда Z_H = Z_cl ~ Z„.

Рассмотрим свойства полузвеньев /л-фильтров и каскадных соединений их с A-фильт­рами. На рис. 5.6, а "[-полузвено /n-фильтра, состоящее из сопротивлений Z₇ и Z₈, кас- кадно соединено с П-фильтром типа к (сопротивления Z₄, Z₅, Z$). На рис. 5.6. б р-полузвено /n-фильтра из сопротивлений Z₉ и Z_l0, каскадно соединено с Т-фильтром типа А (сопротивления Z_H Z_ls Z₃). Сопротивления Z₇ и Z₈ зависят от Z₄ и Z₅, а сопротивления Z₉ и Z_t0 — от Zj и Z₃. Поэтому говорят, что прототипами или Г-полузвеньсв /и-фильтров являются каскадно соединенные с ними А-фильтры.

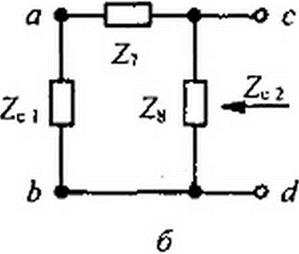
При каскадном соединении фильтров друг с другом всегда соблюдают принцип согла­сованности. Входное сопротивление А-фильтра должно быть равно сопротивлению нагрузки на выходе этого фильтра: Z_c2-Z'_r Для левого полузвена/л-фияьтра Z_c2 является сопро­тивлением нагрузки. Несимметричный четырехполюсник, каким является полузвено /п-фильтра. описывается двумя характеристическими сопротивлениями Z_C1 и Z_c2. Сопро­тивление Z_C1 в /п-фильтре рис. 5.6, а определяется как входное сопротивление схемы рис. 5.7, д, в которой нагрузкой является Z_c2 (входное сопротивление А-фильтра). Сопро­тивление Z_c2 для полузвена /n-фильтра представляет собой входное сопротивление схемы рис. 5.7, б, в которой нагрузкой является Z_cl.

Коэффициенты А, В, С, D “]-полузвена /я-фильтра рис. 5.6, а вычислим по формулам § 4.5, полагая в них Z_}=Z₇, Z₂ = О, Z₃ = Z₈. В результате получим А = I + (Z₇/Z₈). 5 = Z₇, C = l/Z₈, D = l.

Подставим найденные значения А, В, С, D в формулы для Z_c, и Z_c2.

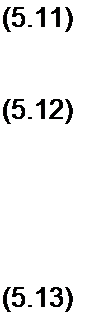Z_cl = VZ₇ Z₈(l ₊ Z₇/Z^;

7 I ^Z?^Z*
^t2 \\ + Z₇IZ_%

Входное сопротивление второго каскада схемы на рис. 5.6, а

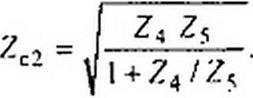
Сопротивление Z₈ в "[-полузвене /л-фильгра (см. рис 5.6, а) берут равным Z$!m. где числовой коэффициент tn находится в интервале от 0 до I. Подставляя в (5.12) Z₅1т вместо Z₈ и приравнивая подкоренные выражения формул (5.12) и (5.13), получим урав­нение для определения Z₇ :

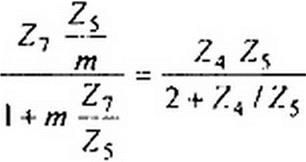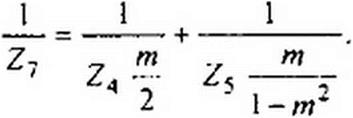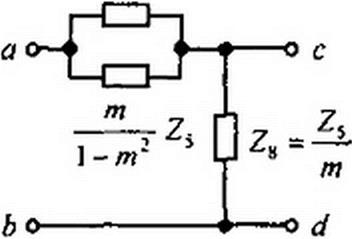
Последнее выражение свидетельствует о том. что сопротивление Z₇ образовано дву­мя параллельно соединенными сопротивлениями Z₄— и Z₅—(рис. 5.7, в). Так как 2 I - т²

Z₇ образовано параллельно соединенными сопротивлениями, которые являются зависи­мыми (производными) от сопротивлений Z₄ и Z₅ А-фильтра, /п-фильтр (см. рис. 5.6, а) называют фильтром параллельно-производного типа.

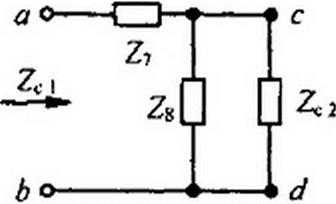
Заменим в схеме на рис. 5 6, а сопротивление Z', - Z_c2 на второе полузвено /л-филь­тра, на входе которого включим согласованную нагрузку Z_H = Z_c) (рис. 5.8, а). Если пер­вое полузвено /л-фильтра схемы на рис. 5.6, а представляло собой "[-полузвено, состоя­щее из сопротивлений Z₇ и Z₈. то второе полузвено /л-фильтра должно представлять собой ["-полузвено, состоящее из тех же сопротивлений Z₇ и Z₈, но как бы переверну­тых относительно вертикальной прямой. Для второго полузвена /п-фильтра входное сопро-

тивление слева равно Z_c2, а входное сопротивление справа (со стороны нагрузки Z_M ) — Z_cl. Практически Z_C1 для фильтра НЧ берут равным его значению при а>->0, а для фильтра ВЧ — его значению при со —>«?. Для т-фильтра (см. рис. 5.6, а) в обоих случаях _с] = ^/2С, где L и С — индуктивность и емкость А-фильтра, являющегося прототи­пом w-фильтра. Для фильтра НЧ — ото значения L и С в схеме на рис. 5.1, б, а для филь­тра ВЧ — в схеме на рис. 5.2, б.

Границы полосы прозрачности у m-фильтра определяют так же, как и у А-фильтра, т. е. полагая Л(со) = ± 1 для фильтров НЧ и ВЧ. В полосе затухания для w-фильтра

ch а = ±Л(о).

Знак минус относится к полосе частот от о_р до о_с, знак плюс — к полосе частот от Ор до оо для филыров НЧ и к полосе частот от ы_р до 0 для фильтра ВЧ (объясняется ото тем, что сопротивление Z₇ изменяет знак при резонансной частоте о_р ). Границы полосы прозрачности по частоте для А-филътра и для каскадно и согласованно с ним со­единенного w-фильтра совпадают. Результирующее затухание всего фильтра а равно сум­ме затуханий т(а_т)- и к{а_к )-фильтров:

Характер зависимости а_т = /(ад) для «-фильтров НЧ и ВЧ показан на рис. 5.8, б, в. где ад_с— частота среза (граничная частота полосы прозрачности). На рис. 5.8, б со_р — резонансная частота, при которой противоположного характера сопротивления — Z.

и —⁸ схеме на рис. 5.7, а вступают в резонанс, так что Z₇ = » (при частоте ) 1 -пг

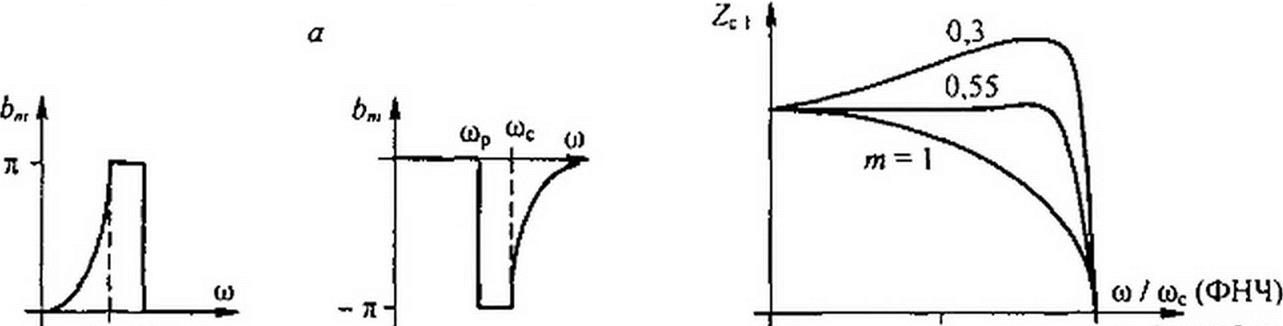
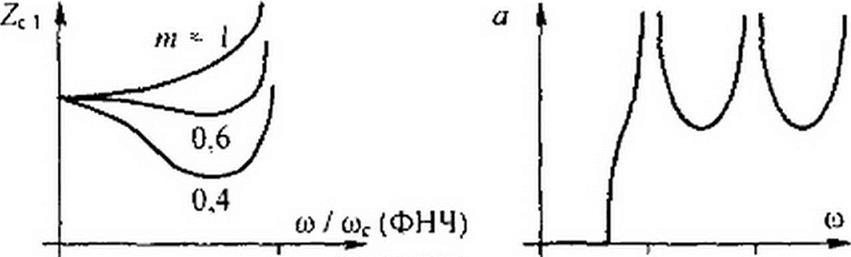
при этом бесконечно велико затухание «-фильтра. В области частот от со_с до w_p затуха­ние а„ резко возрастает, что существенно, так как получается большое затухание в нача­ле полосы затухания, где а_к мало. Уменьшение а_т при to > to_p компенсируется ростом о*. Напряжение на входных зажимах фильтра опережает напряжение на нагрузке на угол Ь = Ь_т + Ь_к, где Ь_т — угол сдвига фаз от «-фильтра, а Ь_к — угол сдвига фаз от А-фильт- ра. Зависимость £*=/(») рассмотрена в §5.3. Зависимость Ь„, = /(ад) показана на рис. 5.8, г для фильтра НЧ и на рис. 5.8, д — для фильтра ВЧ. Зависимость Z_C1 = /(ад/ад_с) для фильтра НЧ показана на рис. 5.9, б при трех значениях т. При т * 0,5+ 0,6 сопро­тивление Z_cl остается приблизительно постоянным почти по всей полосе прозрачности, резко уменьшается только вблизи частоты среза.

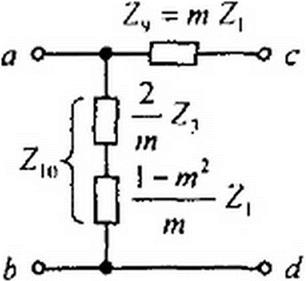
Рассмотрим свойства [“-полузвена /и-фильтра на рис. 5.9, а, являющегося составной частью фильтра на рис. 5.6, б. Опуская промежуточные выкладки, запишем окончатель­ные выражения для Z_c) и Z_c2 этого фильтра:

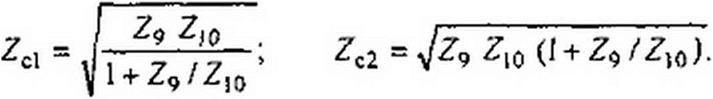Входное сопротивление ^-фильтра (см. рис. 5.6, б)

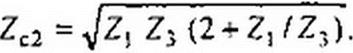(“ -полузвено «-фильтра на рис. 5.9, а называют последовательно-производным, так как его сопротивление Z₎₀ состоит из двух последовательно соединенных сопротивлений 2 l-m²

— Zj и ------------- Z;, являющихся производными от сопротивлений Z> и Z₃ /.--фильтра,

m m

Рис. 5.9

Сопротивления Z, и Z₃ имеют противоположный характер (одно — индуктивный, дру­гое — емкостный), поэтому при некоторой частоте сопротивление Z₁₀ =0 (резонанс на­пряжений). Для полосы прозрачности зависимость Z_cl = /(ад/ад_с) для фильтра НЧ (от to_c /и для фильтра ВЧ) при трех значениях m показана на рис. 5.8, е. При m * (0,5+ 0.6) Z_C| относительно мало изменяется в полосе прозрачности, чзю важно для практики. За­висимости = /(ад) и b„, = /(to) для «-фильтра на рис. 5.6, б такие же, как и для соот­ветствующего ему «-фильтра на рис. 5.6, а. Обобщенно можно сказать, что теоретически бесконечно большое затухание в /п-фильтрс на частоте м_р создается либо за счет того, что на этой частоте в последовательной ветви полузвена «-фильтра оказывается участок с бесконечно большим сопротивлением (возникает резонанс токов), либо за счет того, что параллельная ветвь «-фильтра образует короткое за.мыкаяие при возникновении в ней режима резонанса напряжений. При каскадном соединении нескольких /п-фильтров значения L, С выбирают различными, чтобы создавать большие затухания на нескольких заданных частотах (о)_р1, о_р2 и т. п.). При этом зависимость а- /(о), например, для фильтра НЧ имеет вид гребенки (рис. 5.9, в). Фильтр с такой характеристикой иногда на­зывают гребенчатым.