Электрические фильтры
§ 5.1 Назначение и типы фильтров. Под электрическими фильтрами понимают четырехполюсники, включаемые между источником питания и приемником (нагрузкой), назначение которых состоит в том, чтобы беспрепятственно (без затухания) пропускать к приемнику токи одних частот и задерживать или пропускать, но с большим затуханием, токи других частот.
Диапазон частот, пропускаемых фильтром без затухания, называют полосой прозрачности; диапазон частот, пропускаемых с затуханием, — полосой затухания.
Электрические фильтры собирают обычно из индуктивных катушек и конденсаторов. Исключение составляют /?С-фильтры (см. § 5.6-5.9), Фильтры используют главным образом в радиотехнике и технике связи, где применяют токи довольно высоких частот.
При высоких частотах индуктивные сопротивления L индуктивных катушек во много раз больше их активных сопротивлений. Поэтому будем полагать, что активные сопротивления индуктивных катушек и активная проводимость конденсаторов равны нулю, т. е. что фильтры составлены только из идеальных реактивных элементов.
Фильтры обычно собирают по симметричной Т- или П-схеме (рис. 4.4, а, б), т. е. при Z2 - Z, и Z6 - Z5.
При изучении фильтров будем пользоваться понятием коэффициента затухания и коэффициента фазы (см. § 4.10).
Условимся сопротивление Z\ в схеме (см. рис. 4,4, а) и сопротивление Z4 в схеме (см. рис. 4.4, б) называть продольными, а сопротивление Z- в схеме (см. рис. 4.4, а) и сопротивление Z5 в схеме (рис. 4.4, б) — поперечными.
Фильтры, в которых произведение продольного сопротивления на соответствующее поперечное сопротивление представляет собой некоторое постоянное для данного фильтра число (число А), не зависящее от частоты, принято называть к-фильтрами.
Сопротивление нагрузки ZH, присоединяемой на выходе фильтра, должно быть согласовано с характеристическим сопротивлением фильтра Zc (ZH-ZC). Входное сопротивление /t-фильтра при этом также равно Zc. В А-фильтрах Zc существенно изменяется в зависимости от частоты to, находящейся в полосе прозрачности. Это обстоятельство вызывает необходимость изменять сопротивление нагрузки в функции частоты (особенно при приближении к границе полосы прозрачности), что нежелательно. В /w-фильтрах при определенных значениях коэффициента т сопротивление Zc мало изменяется от частоты (в пределах
полосы прозрачности), поэтому нагрузка практически может быть одна и та же по модулю для различных со, находящихся в этих пределах.
Качество фильтра тем выше, чем более резко выражены его фильтрующие свойства, г. е. чем более резко возрастает затухание в полосе затухания.
Фильтрующие свойства четырехполюсников обусловлены возникновением в них резонансных режимов — резонансов токов или резонансов напряжений.
§ 5.2 Основы теории А-фильтров. Из § 4.10 известно, что если нагрузка ZH согласована с характеристическим сопротивлением Zc четырехполюсника, то напряжение й2 и ток в нагрузке /, связаны с напряжением и током /( на входе четырехполюсника следующими соотношениями:
^2 ~ ^1 е » ^2 = А е »
где g - In (А + 7# О а а + j b.
Тогда
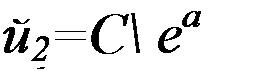 | |||
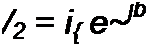 | |||
Множитель е-" определяет, во сколько раз модуль напряжения (тока) на выходе фильтра меньше модуля напряжения (тока) на его входе.
Если а = 0, то е-й = е° = 1 и фильтр пропускает колебания без затухания. Таким образом, в полосе прозрачности а - 0.
В полосе затухания я>0. Множитель е~/Л, по модулю равный 1, свидетельствует о том, что напряжение 02 и ток А отстают соответственно от и /( на угол Ь.
Фильтрующие свойства четырехполюсника рассмотрим, сравнивая выражения для коэффициента А четырехполюсника с равным ему выражением гиперболического косинуса от аргумента а + j b:
А - ch {а + j b).
Гиперболический косинус от суммы двух аргументов (с учетом того, что ch j b - cosZ> и sh j b = j sin b ) можно представить следующим образом:
ch {а + j b) = ch a cos b + j sh a sin b.
Для любого фильтра, собранного по Т-схеме (см. §4.5), // = 1 + (Z1/Z1).
Для фильтра, собранного по П-схеме (см. § 4.5), А - I + (Z4 /Z5). Из каких бы реактивных сопротивлений ни был собран фильтр, отношения Z, /Z3 в Т-схеме и Z4 /Z5 в П-схеме всегда будут действительными (не мнимыми и не комплексными) числами — отношение двух мнимых чисел всегда есть число действительное. Следовательно, всегда будет дей-
| ствительным и коэффициент А. Но если коэффициент А действителен, то действительным должно быть и выражение равного ему ch(a + j b)i |
| ch (a + j b) - ch a cosb + J sh a sin b = A. |
| Это выражение действительно, если |
| sh a sin b - О, |
| (5.1) |
| При этом |
| ch a cos b = А. |
| (5.2) |
| Уравнения (5.1) и (5.2) используют для определения границ полосы прозрачности и характера изменения угла b в этой полосе, а также характера изменения коэффициента затухания в полосе (полосах) затухания. Равенство (5.1) для полосы прозрачности {а - 0) удовлетворяется, так как sh а = sh 0 = 0. В силу того что chO = 1, уравнение (5.2) для полосы прозрачности переходит в следующее: |
| cos b = А. |
| (5.3) |
| Круговой косинус (cosb) может изменяться в пределах от + 1 до - 1. Поэтому крайние значения коэффициента А (являющегося функцией частоты -Л(со)) в полосе прозрачности равны ±1. Полоса прозрачности в общем случае лежит в диапазоне частот от со1 до <о2- Значения со, и (в2 для фильтров НЧ и ВЧ (подробнее см. § 5.3) определяют решением уравнений |
| А (со) = ± I. |
| (5.4) |
| Для полосовых и заграждающих фильтров (см. § 5.3) (В) и д>2 находят как корни уравнения Л(й)) = -1. Частоту, являющуюся граничной между полосой прозрачности и полосой затухания, называют частотой среза. Характер изменения угла b в функции со для полосы прозрачности определяют в соответствии с уравнением (5.3) следующим образом: |
| b = arccos Л(со). |
| (5-5) |
| Определим а и Ь для полосы затухания. В полосе затухания а > 0. Уравнение (5.1) удовлетворяется при условии |
| sin b = 0, |
| (5.6) |
| т. е. при |
| (5-7) |
| и (или) при |
| Ь = ± я. |
| (5-8) |
Согласно уравнению (5.2), при Ь = О
cho = ^(co). (5.9)
а при Ь = ± к
ch а - -Л(со). (5.10)
Уравнения (5.9) и (5.10) позволяют по значениям А как функции со рассчитать ch а в полосе затухания, а по cho определить а и, таким образом, построить кривую а- /(со). Из уравнений (5.7) и (5.8) следует, что в полосе затухания напряжение U-> на выходе фильтра находится либо в фазе (при Ь = 0 )> либо в противофазе (при b - ± л ) с напряжением 0} на входе фильтра.
В заключение необходимо отметить два важных положения:
1) с изменением частоты со меняются коэффициенты В и С четырех- полюсника, поэтому изменяется и характеристическое сопротивление Zc = уГвТс. Для того чтобы фильтр работал на согласованную нагрузку (только в этом случае справедлива изложенная теория фильтров), при изменении частоты необходимо менять и сопротивление нагрузки;
2) в полосе прозрачности характеристическое сопротивление 4-фильтров (§ 5.3) активное, а в полосе затухания — чисто реактивное (индуктивное или емкостное).
Если нагрузка фильтра не чисто активная или не согласована с характеристическим сопротивлением фильтра и если требуется учесть влияние активного сопротивления индуктивных катушек на работу фильтра (что существенно для низких частот), то для построения зависимости (7, /и2 - /(д>) и зависимости сдвига фаз между £7, и (У2 в функции частоты можно воспользоваться, например, методом пропорциональных величин (см. пример 57). Характеристическое сопротивление фильтра берут равным внутреннему сопротивлению источника сигнала (генератора). Яри этом и генератор и фильтр работают в режиме согласования.
§ 2.3 tf-фильтры НЧ и ВЧ, полосно-пропускаюицие и полосно-за- граждающие А-фильтры. Фильтрами НЧ (ФНЧ) называют фильтры, пропускающие в нагрузку лишь низкие частоты: с <о, =0 до о)2. Полоса их затухания находится в интервале от со2 до ос
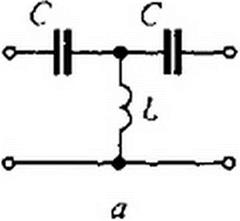
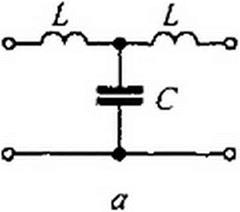
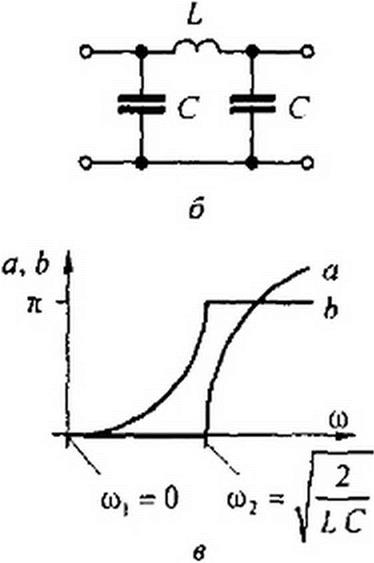
Схемы двух ФНЧ приведены на рис. 5.1, а, б. Характер изменения коэффициента затухания а и коэффициента фазы Ъ качественно иллюстрируют кривые рис. 5.1,
Под фильтром ВЧ (ФВЧ) понимают фильтры, пропускающие в нагрузку лишь высокие частоты: с со( до ос Полоса затухания их находится в интервале от 0 до
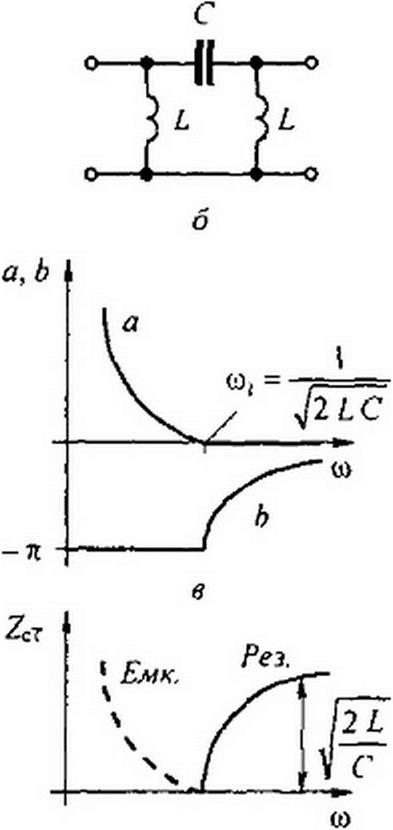
Схемы двух ФВЧ приведены на рис. 5.2, а, б. Характер изменения коэффициентов а и b для них иллюстрируют кривые рис. 5.2, в.
Рассмотрим вопрос об изменении модуля характеристического сопротивления Zc в полосе прозрачности для Т-фильтра НЧ (см. рис. 5.1, а)
 | |||||||
 | |||||||
 | |||||||
 | |||||||
|
 | |||
 | |||
|
и для Т-фильтра ВЧ (см. рис. 5.2, а), а также для П-фильтров. С этой целью в выражение Zc = Jb/C подставим значения В и С в соответствии с формулами (4.35), (4.37) и проанализируем полученные выражения.
ГГд J 2
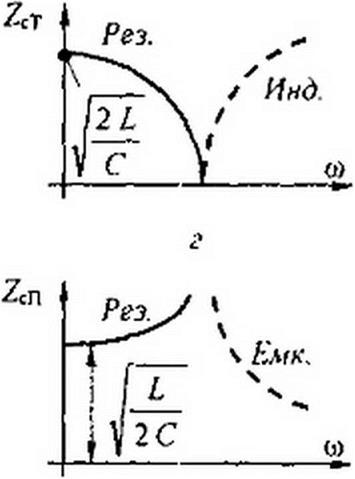
Для Т-фильтра НЧ (см. рис. 5.1, а) ZcT = J'ТГ “w - График ZcT ~ /(<») представлен на рис. 5.1, г. ’
При о = (0| =0 ZcT = ^2 LIC. С увеличением частоты ZcT уменьшается, сначала мало отличаясь от значения ^2 L/C. При достижении значения о = о, = J2ILC Z. - 0.
< 2 С У0,5
Для П-фильтра НЧ (см. рис. 5.1, 6) Zcn = — -<о2 С2 . График ^сп =/(®) Дан на рис. 5.1, <). 'ч
 Для Т-фильтра ВЧ (см. рис. 5.2, a) ZcT = ZcT - /(to) дан на рис. 5.2, г.
Для Т-фильтра ВЧ (см. рис. 5.2, a) ZcT = ZcT - /(to) дан на рис. 5.2, г.
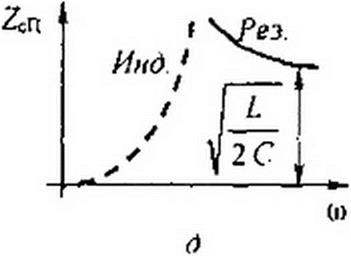
В этом случае характер изменения ZcT отличен от характера изменения ZcT для Т-фильтра НЧ, а именно ZcT =0 при o^toj ~ \ / ^2 LC. С увеличением w сопротивление ZcT увеличивается и при (о->со zcT = рис.








