§ 4.18 Построение дуги окружности по хорде и вписанному углу. Из курса геометрии известно, что вписанным углом называют угол, вершина которого находится на окружности, а стороны являются хордами.
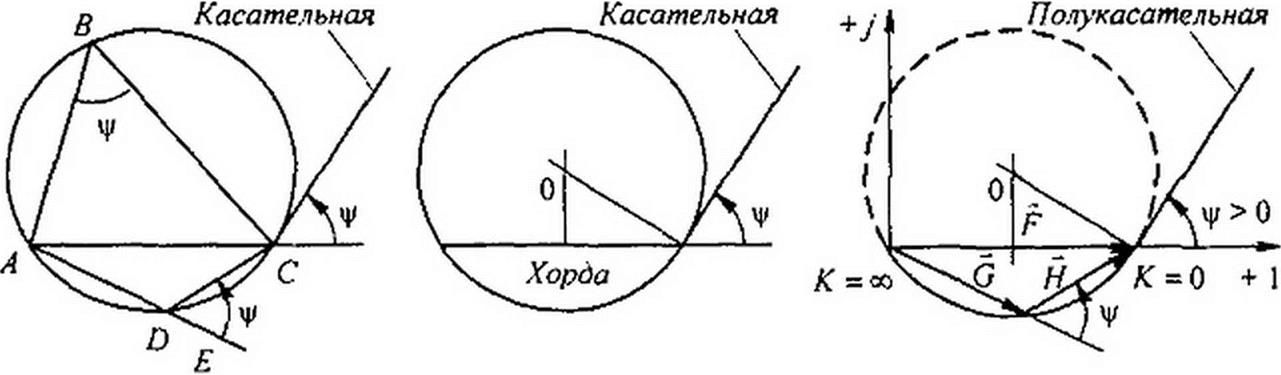
Вписанный угол измеряется половиной дуги, на которую он опирается. Так, Z.ABC = ц/ (рис. 4.18, а) измеряется дугой ADC/2, a Z.ADC — дугой АВС/2. Сумма ЛАОС + ЛА ВС - тс.
 |
|
Угол Z.EDC дополняет до л угол Z^DC, поэтому Z.EDC - ф.
Какое бы положение ни занимала точка D в интервале от А до С, угол между продолжением хорды AD (т. е. линией DE) и хордой DC остается неизменным и равным
Угол между продолжением хорды АС и касательной (полукасательной) к окружности в точке С также равняется углу V-
Центр окружности О находится на пересечении перпендикуляра к середине хорды и перпендикуляра к касательной (рис. 4.18, б).
Из изложенного следует, что если заданы хорда и вписанный угол ЧА то для нахождения центра окружности необходимо:
1 ) восставить перпендикуляр к середине хорды;
2 ) под углом V к продолжению хорды провести прямую, которая будет являться касательной к окружности;
3 ) восставить перпендикуляр к касательной; пересечение перпендикуляра к хорде и перпендикуляра к касательной даст центр окружности.
4 4.19. Уравнение дуги окружности в векторной форме записи. Построения, аналогичные построениям на рис. 4.18, а, могут быть выполнены и на комплексной плоскости. В этом случае все хорды, например, СА, DA, DC являются векторами.
На комплексной плоскости (рис. 4.18, в) совместим хорду СА - F с осью + 1. Если угол ф > 0, то от продолжения хорды его откладывают против часовой стрелки; если угол откладывают по часовой стрелке.
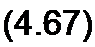 Обозначим DA-G и CD=H. Тогда
Обозначим DA-G и CD=H. Тогда
G + Н -F.
Вектор Н опережает вектор G на угол У- Пусть модуль вектора Н будет в к раз больше модуля вектора G. Тогда
(4.68)
Если к - 0, то /7 = 0 и G - F. При к = ъ Н -F и G = 0. Подставив (4.68) в (4.67), получим
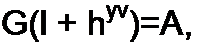 | |||
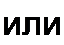 | |||
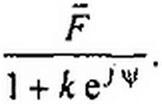 (4.69)
(4.69)
Уравнение (4.69) называют уравнением дуги окружности в векторной форме записи.
При изменении коэффициента А от 0 до со меняются оба вектора G и Я, но так, что угол ф между ними остается неизменным, а сумма векторов равна вектору F. Конец вектора G скользит по дуге окружности, хордой которой является вектор F. Поэтому можно сказать,_что дуга окружности является геометрическим местом концов вектора G.
Рабочей частью окружности, или рабочей дугой, является та часть окружности, которая по отношению к хорде лежит по обратную сторону от полу касательной (рабочая дуга на рис. 4,18, в вычерчена сплошной линией, нерабочая — штриховой линией).
Рабочая дуга меньше половины окружности при | уj < 90° и больше половины окружности при | ц/1 > 90°.
5 4.20. Круговые диаграммы. Из § 3.4 известно, что синусоидально изменяющиеся функции времени (токи, напряжения) могут быть изображены векторами на комплексной плоскости. Если процесс в электрической цепи описывается уравнением, по форме тождественным уравнению (4.69), то геометрическим местом концов вектора тока (напряжения), выполняющего в уравнении электрической цепи те же функции, что и вектор G в уравнении (4.69), является окружность.
Под круговой диаграммой тока или напряжения понимают дугу окружности, являющуюся геометрическим место концов вектора тока (напряжения) при изменении по модулю какого-либо сопротивления электрической цепи и сохранении неизменными остальных сопротивлений, частоты и ЭДС источников энергии.
С помощью круговых диаграмм производят графический анализ работы электрических цепей.
6
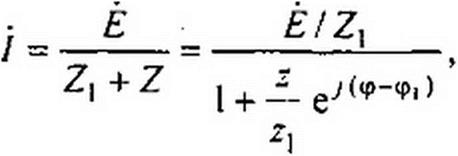 | |||
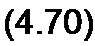 | |||
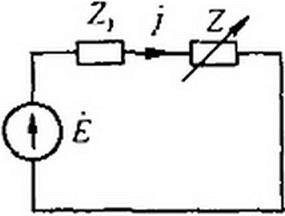
4.21. Круговая диаграмма тока двух последовательно соединенных сопротивлений. Пусть к источнику ЭДС подключены последовательно Z} = и Z = ze7<p (рис. 4.19). Сопротивление Z( неизменно, a Z может меняться лишь по модулю, так что угол ф остается постоянным. Ток в цепи
• •
где Е! Zj = Ik - ток в цепи при коротком замыкании сопротивления Z.
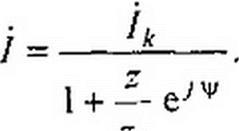
|
Обозначим ф-ф, ^ф. Тогда
(4.71)
Уравнение (4.71) тождественно (4.69). Роль вектора F выполняет комплекс 7t; роль коэффициента к — отношение z/z.; роль G — вектор 7. При изменении z вектор 7 будет скользить по дуге
|
окружности, хордой которой является 1к.
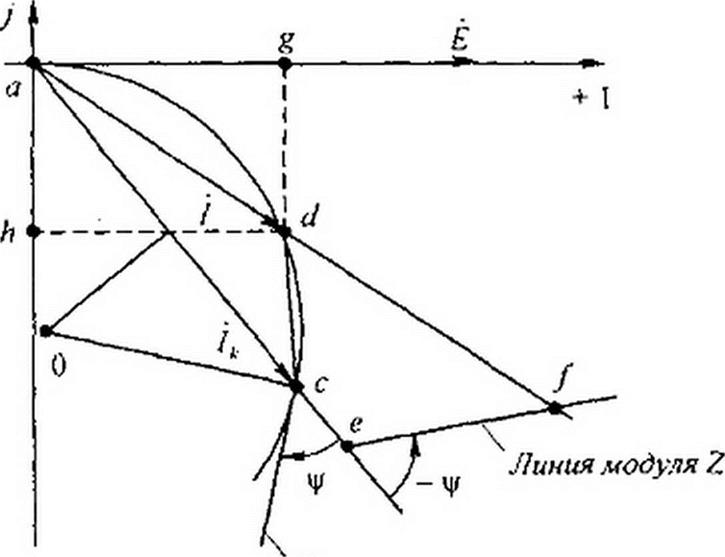
На круговой диаграмме рис. 4.20 вектор ЭДС направлен по оси + 1. Ток -Ё/х}е/ч>> отстает от ЭДС Ё на угол фР Для определенности построим диаграмму при ф <0. Выберем масштаб токов: пусть отрезок ас в масштабе выражает собой модуль тока 7а.. Отрезок da характеризует модуль тока 7, отрезок cd в соответствии с уравнением (4.71) — мо
дуль произведения 7— с7'1*. Отложим по направле- нию 1к отрезок ае в произвольном масштаое т:, выражающий модуль постоянного сопротивления zt (zl ~ает.).
Из точки е под углом - ф к линии ае проводим прямую ef которая является (как будет показано далее) линией модуля переменного сопротивления z при отсчете отточки е. На ней в масштабе нанесем деле
ния для измерения z.
Из подобия треугольников a de и aef следует
| ad ае de ef ’ |
| или z = efmz. |
| Пол vкаса me.t ьная |
| Ряс. 4.20 |
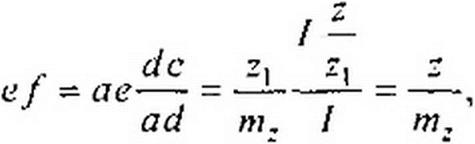
Следовательно, отрезок ef в масштабе т. определяет модуль переменного сопротивления z.
Проекция / на направление Ё (отрезок ag) в масштабе mp = Emi измеряет активную мощность:
Р = ag т = ag Е = ag Е—-Е1 cos <p; — —-costp.
ad ad aq
Проекция / на направление, перпендикулярное Ё (отрезок ah), в масштабе тр определяет реактивную мощность:
Q~ ah тр = ah Е (1 / ad) = Е 1 sin q>.
§ 4.22 Круговая диаграмма напряжения двух последовательно соединенных сопротивлении. Умножив обе части уравнения (4.71) на Zj = zj еуф| и учтя, что i Z} = C’:i, получим
(4.72)
“_РЛФ-Ф1)
-I
Уравнение (4.72) свидетельствует о том, что геометрическим место концов вектора (?.| является дуга окружности, хорда которой Ё.
§ 4.23 Круговая диаграмма тока активного двухполюсника. Ток
в цепи нагрузки ZH = 21(е'ф" активного двухполюсника (рис. 3.30, а)
(4.73)
1 4- ">1 еЛФи-<₽вх )
где ZBX =zBX е7Фв' — комплексное входное сопротивление двухполюсника по отношению к зажимам ab выделенной ветви.
Из уравнения (4.73) следует, что при изменении модуля сопротивления нагрузки zH ток /н скользит по дуге окружности.
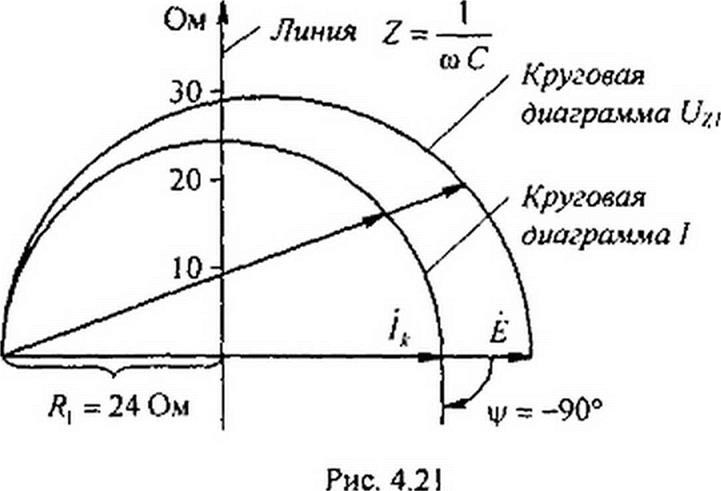
Пример 53. В схеме (рис. 4.19) Ё = 120 В; Z{= R\~ 24 Ом; сопротивление Z — чисто емкостное, модуль его изменяется от 0 до оо. Построить круговые диаграммы тока и напряжения на сопротивлении Z}.
Решение. Ток = 120/24 - 5 А Выберем масштаб для токов (т, = 1.39 А/см) и напряжений (тг/ = 26 В / см).
Найдем угол
Ф = ф - ф, = -90й - 0° = -90°.
На рис. 4.21 построены круговая диаграмма тока на токе !к как на диаметре и круговая диаграмма напряжения на ЭДС Ё как на диаметре. Масштаб для сопротивлений т. = 13 Ом/см. Для любого значения сопротивления z по диаграмме находим юк / и напряжение и.л. Так, при z = 9.5 Ом / = 4,65 A. U:} = 111,5 В.
 | |||
 | |||
|
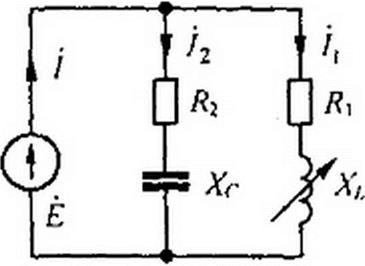
Пример 54. Построить геометрическое место концов вектора тока / неразветвлен- ной части схемы (рис. 4,22) и графически исследовать возможность возникновения резонансных режимов при следующих данных: £ = 30 В; £2 = 6Ом; .V(-=8Om; £] = 3 0м; X j изменяется от 0 до со.
 |
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
| ||||||||||||
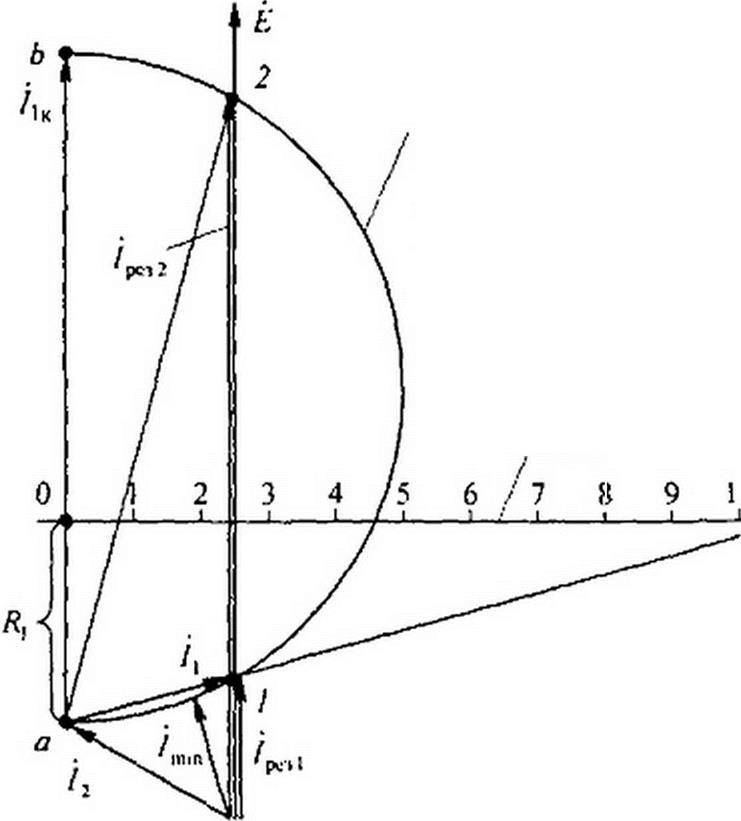
Решение. Ток Д в схеме остается неизменным: /2 ~ 30/(6 -j8) = 3ej53 10 А. Он на 53° 10' опережает ЭДС £ (рис. 4.23).
Вектор тока /, при изменении .V/ меняется так, что коней его скользит по дуге окружности. диаметром которой является вектор тока: /ц = £/£( = )0 А. гв/ = 2,65 А/см.
Ток в неразветвленной части схемы / = /, + /2. Геометрическим местом его является также дуга окружности а 12 Ь. В режимах, соответствующих точкам / и 2, ток / совпадает по фазе с ЭДС £. Следовательно, в этих режимах в схеме имеет место резонанс токов.
Выберем масштаб сопротивлений т. =2Ом/см. Графически найдем Х( для точек / и 2. Для точки 2 Xу ~ 0,8 Ом. для точки / Л'/ = 10,6 Ом. При этом ток J = 11,1 и 2.4 А.
§ 4,24. Круговая диаграмма напряжения четырехполюсника. Пусть напряжение на входе четырехполюсника на рис. 4.2, а неизменно по модулю, фазе и частоте, а нагрузка Z2 = г2 с'Фг на выходе его изменяется только по модулю, так что характеризующий ее угол ф2 остается постоянным. В этом случае для тока /2, напряжения (Д, тока /( могут быть построены круговые диаграммы. Сначала рассмотрим круговую диаграмму тока /2. С этой целью схему четырехполюсника (рис. 4.2, а), исключая нагрузку Z2, заменим активным двухполюсником и по методу эквивалентного генератора найдем ток /2 в ветви рд:
(4.74)
где Uрчк — напряжение между точками р и д при размыкании ветви рд; ZBXM = Z2KcJ^1K — входное сопротивление по отношению к зажимам рд при короткозамкнутых зажимах мп (в схеме на рис. 4.2. а к зажимам тп присоединен источник ЭДС). Разделив числитель и знаменатель правой части (4.74) на 7ъхр<{=7гк и учтя, что /Z2>t = /2к, где /2к — ток короткозамкнутой ветви рд, получим
(4.75)
Из уравнения (4.75) следует, что вектор тока /2 скользит по дуге окружности, хордой которой является ток /2к.
Построим круговую диаграмму тока Д на входе четырехполюсника. Из предыдущего (см. формулу (2.25)) известно, что при изменении сопротивления в одной из ветвей линейной электрической цепи два тока в любых двух ветвях этой цепи связаны соотношением 1„=а + Ы„. Следовательно, ток /, может быть линейно выражен через ток ;
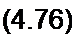 • 9
• 9
/] = а + b /2.
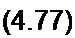 Определим коэффициенты а и Ь. Если ветвь рд разомкнута, то /2 =0 и /( = /)х. При этом из (4.76) найдем о = /2х. Если ветвь рд короткозамкнутая, то = и А = Ак- Поэтому
Определим коэффициенты а и Ь. Если ветвь рд разомкнута, то /2 =0 и /( = /)х. При этом из (4.76) найдем о = /2х. Если ветвь рд короткозамкнутая, то = и А = Ак- Поэтому
Ак “ Ах + Aix-
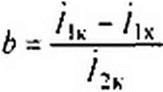 Отсюда
Отсюда
(4.78)
Подставив (4.77) и (4.78) в (4.76), получим
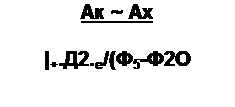 | |||||
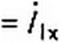 | |||||
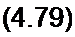 | |||||
Уравнение (4 79) свидетельствует о том, что геометрическим .местом концов вектора тока /| также является дуга окружности. Хордой ее является разность /1и -/]х; вектор /1х смещает начало отсчета.
Аналогичным образом строят круговую диаграмму напряжения. Так. если в какой-то схеме изменяется по модулю сопротивление Z, =2ге'ф2 в одной, например второй, ветви, то для напряжения на участке ab этой схемы можно записать выражение, анало*
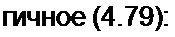 |
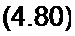 UobK-Ugb*
UobK-Ugb*
| 4. ~2 е/('₽2 "Фп > г2к
где С'пА< — напряжение на зажимах ab при z2 = °°; ^'аЬк — напряжение на зажимах ab при з2 =0; Z2k =?2Ke-'<₽I* — выходное сопротивление схемы относительно зажимов, к которым присоединено сопротивление Z2.
Формула (4.80) выведена на основании выражения Ua/t - a, +h. /2 и (4.74).
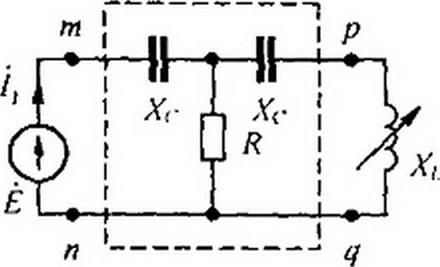
Пример 55. Построить круговую диаграмму тока Д схемы (рис. 4.24, а), в которой Л7 =5 0м; Я = 5Ом; £ _ 100 В. Нагрузкой четырехполюсника является индуктивное сопротивление Xt, которое может изменяться от 0 до ».
 |
| ||||
| ||||
 |
| ||||
| ||||
Решение. Найдем ток холостого хода при разомкнутой выходной ветви:
/1х =E/(R~jXc) = 100/(5-у5) = 14,15е>45° А.
Определим ток короткого замыкания при коротком замыкании нагрузки:
 ~-------- — = )2,82e/7|°2t> А.
~-------- — = )2,82e/7|°2t> А.
/?(-73Н
*-м<-
Рассчитаем входное сопротивление Z2ti со стороны зажимов pq при коротком замыкании зажимов тп:
ZnK = е'ф2‘ = -JXC + -^-Л-(■ - = 7.8е“77’’20' Ом.
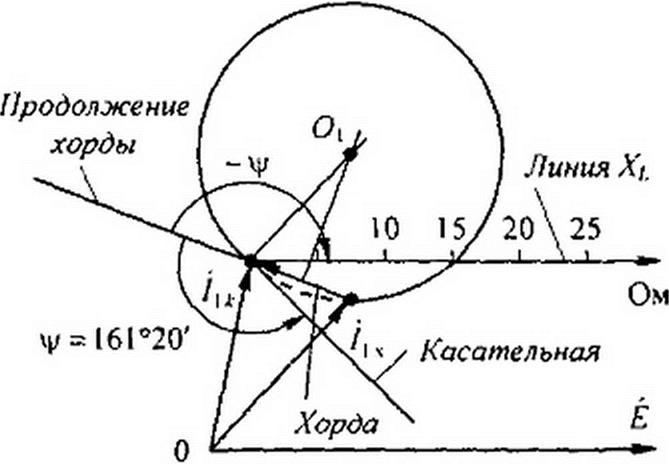
Следовательно. <р2х = -71’20'. Угол у = <р2 - <р2(. = 90° - (-71°20’) = 161®20‘.
Круговая диаграмма тока /} построена на рис. 4.24. б. Хордой окружности является разность /|к-/1х. Угол ч/>0, поэтому для определения положения касательной он отложен от продолжения хорды против часовой стрелки. Диаграмма носит несколько необычный характер: рабочая часть дуги занимает почти целую окружность.
Для определения положения конца вектора из конца вектора /)х через точку на линии Xt, соответствующую заданному значению Л'?, проводят прямую до пересечения с рабочей частью дуги окружности. При Xt =5 Ом ток Ц опережает ЭДС Е на 90’.
§ 4.25. Линейные диаграммы. Под линейными диаграммами понимают диаграммы, в которых геометрическим местом концов вектора тока (напряжения) является прямая линия. По существу, линейная диаграмма является частным случаем круговой, поскольку прямая есть дуга окружности с бесконечно большим радиусом.
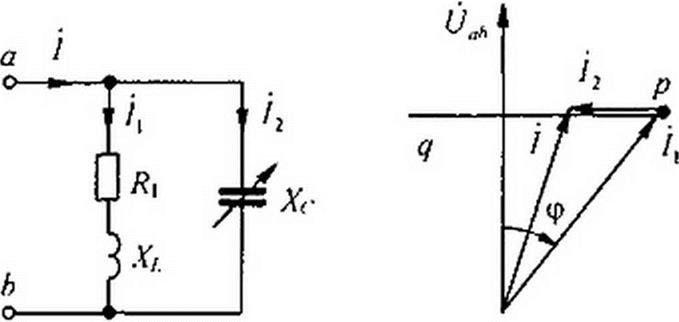
Пример 56. Построить геометрическое место концов вектора тока в схеме на рис. 4.25, а при изменении Х(-. Напряжение Uaf)= const, /?, и Х{ неизменны.
Реше н не. На рис. 4.25, б изображаем вектор йаЬ. Вектор тока /, отстает от него
а б
Рис. 4.25
на угол <p = arctgXL/Я].
Ток /2 опережает на 90°. Геометрическим местом концов вектора тока / = /( + /2 будет прямая линия pq. Она и является линейной диаграммой тока /.
Вопросы для самопроверки
I. Запишите шесть форм записи уравнений четырехполюсника, покажите для них положительные направления отсчета токов и напряжений и поясните, в каких случаях каждая форма записи имеет преимущества перед остальными. 2. Какие четырехполюсники называют взаимными, невзаимными, симметричными и несимметричными? 3. Как опытным путем определить коэффициенты Z-, К-. Н-, G-, 5-форм записи? 4. Каким образом. зная коэффициенты одной формы записи, определить коэффициенты другой формы? 5. Прокомментируйте схемы замещения пассивных четырехполюсников. 6. Какое соединение четырехполюсников называют регулярным? 7. Что понимают под Zc} и Zc2 несимметричного четырехполюсника и как их определить через коэффициенты Я, 5. С, D и через входные сопротивления? 8. Что понимают под повторным сопротивлением четырехполюсника? 9. Запишите уравнения для симметричного четырехполюсника через гиперболические функции. 10. Запишите уравнения для несимметричного четырехполюсника через гиперболические функции. 11. Что понимают под постоянной передачи симметричного и под мерой передачи несимметричного четырехполюсников? 12. В каких единицах измеряют затухание? Как эти единицы связаны между собой? 13. Охарактеризуйте свойства конвертора, инвертора и гиратора. 14. Дайте характеристику операционному усилителю как элементу электрической цепи. 15. Каким расчетным схемным эквивалентом может быть замещен ОУ? 16. Охарактеризуйте свойства управляемых источников напряжения и тока. 17. Покажите, что схема на рис. 4.12 может выполнять функции гиратора. 18. Поясните, почему схема на рис. 4.14 может выполнять функции ИНУТ, схема на рис. 4.15, а — функции ИНУТ. схема на рис. 4.15, о — функции ИТУН. а схема на рис. 4.15, в — функции конвертора отрицательного сопротивления. 19. В схеме на рис. 4.Ц Z2 = Z4 - Zs = R. Какими следует взять Z| = Zj, чтобы входное сопротивление схемы ZAH было отрицательным, чисто резистивным и пропорциональным 1 /се*’? 2Q. Каким следует взять сопротивление Z2 = Z4 в схеме на рис. 4.11 (Z, = Z3 = Z5 = R). чтобы входное сопротивление схемы Zл1! было отрицательным, чисто резистивным и пропор
циональным о)2? 21. Какой четырехполюсник называют активным автономным и какой активным неавтономным? 22. Запишите систему уравнений многополюсника в У-форме и поясните, как определить его У^- и Ypr- параметры. 23. Дайте определения активного автономного и активного неавтономного многополюсника. 24. Запишите уравнение дуги окружности в векторной форме и поясните его. 25. Сформулируйте условия, при которых можно строить круговую диаграмму. В чем преимущества исследований цепей с помощью круговых диаграмм? 26. Поясните последовательность построения круговой диаграммы двухполюсника и четырехполюсника. 27. Как определить рабочую часть дуги окружности? 28. Как определить масштаб на линии переменного сопротивления? 29. При каком условии круговая диаграмма переходит в линейную? 30. Решите задачи 6.4; 6.9; 6.13; 6.23; 6.35; 6.38.
Глава пятая








