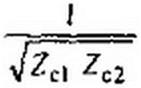При регулярном соединении матрица каждого четырехполюсника должна оставаться такой же, какой она была до соединения четырехпо­люсников.

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

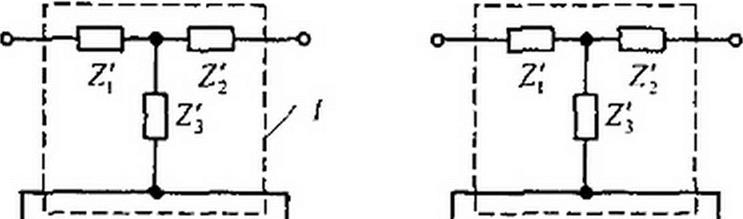
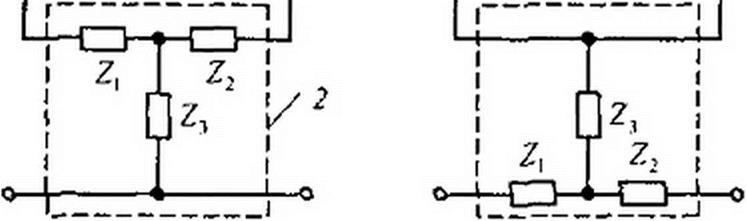
Пример нарушения условия регулярности при последовательно-по­следовательном соединении показан на рис. 4.6, а. Так соединять четырехполюсники 7 и 2 нельзя, поскольку входные зажимы второго четырехполюсника оказались накоротко соединенными с его выходны­ми зажимами.

Регулярное соединение тех же четырехполюсников показано на рис. 4.6, б — перекрещены обе пары концов второго четырехполюсника (при перекрещивании обеих пар концов все элементы любой матрицы остаются неизменными).

§ 4.9 Характеристические и повторные сопротивления четырех­полюсников. В случае несимметричного четырехполюсника (Л * D) рассматривают два характеристических сопротивления— Z_cI и Z_c2, где Z_ct — входное сопротивление со стороны зажимов тп, когда нагрузка подключена к зажимам pq и равна Z_e2 (рис. 4.7, а):

_{z = =} л h ₌ * z__c^b .

^с ' /] cu₂ + di₂ cz_c2 + d'

Z_c2 — входное сопротивление co стороны зажимов pq, когда нагрузка Z_d подключена к зажимам тп (рис. 4.7, б); при этом коэффициенты А и D меняются местами:

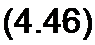PU₂+B 1₂ _ DZ_c[+B

CU₂ + Af₂ ” С Z_d + А ‘

Совместно решая (4.45) и (4.46), найдем

Z_CI = JaBICD-, = JDB/CA. (4.47)

Учитывая, что J/C = Z_)x, S/Z) = Z_lK, £/J = Z_2k, Z)/C = Z_2x, по­лучим

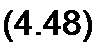Если четырехполюсник симметричен (Л = D), то

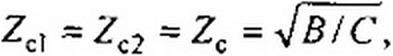где Z_c равно входному сопротивлению четырехполюсника, когда он на­гружен на Z_c (рис. 4.7, в).

В теории цепей иногда пользуются понятием повторного сопротив­ления четырехполюсника Z_n0B. Под ним понимают входное сопротивле­ние со стороны зажимов тп, если к выходным зажимам pq присоедине­но Z_noB. Из формулы (4.45), заменив в ней Z_cl и Z_c2 на Z_n0B, получим

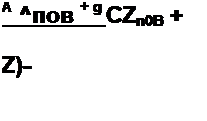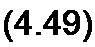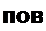Решив (4.49) относительно Z_no8, найдем

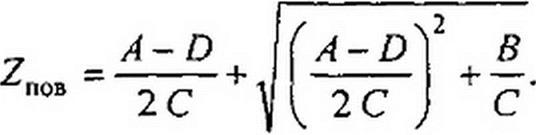Если четырехполюсник симметричный (Л = £>), то Z ~ yjB/C, т. е. оно совпадает с характеристическим сопротивлением Z_c. Сопротив­ление Z_n0B называют повторным потому, что оно повторяет сопротивле­ние нагрузки на выходе четырехполюсника.

§ 4.10 Постоянная передача и единицы измерения затухания. Для симметричного четырехполюсника, нагруженного на Z_c,

Ц = AV₂ + B/₂ = U₂(A + JbC); /, =Л(/1 + 7вС).

Комплексное число А + ВС полагают равным e^g, где g = а + jb = In (А + у/ВС) — постоянная передачи.

Из формул й_} -й₂ е° е^уЛ; /₍ = /₂ ^е° ^е'^/Л следует, что модуль й_} в е^а раз больше модуля (/₂, а модуль /, в е" раз больше модуля /₂. По фазе Ц опережает (]₂ на угол Ь, ток /, опережает /₂ также на угол Ь.

Величина а характеризует затухание четырехполюсника. Единицами затухания являются неперы (Нп) и белы (Б). Неперы определены на основе натуральных логарифмов, а белы — на основе десятичных. Зату­хание в неперах

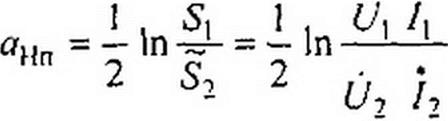При согласованной нагрузке

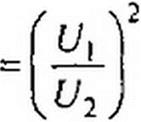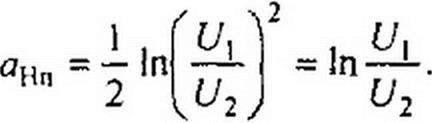Если (J\/U₂ ~ е, то затухание равно 1 Нп. Затухание в белах

а_Е = IgfS, /S₂) = lg(t/, /4Л,)² = 2 Igft/,W₂|,

а в децибелах я_дБ = 20 lg (£7_t / С₂).

Если t/| больше С₂ в 10 раз, то затухание равно 20 дБ, если Ц/(/₂ = 100, то а = 40 дБ.

Выразим неперы через белы. Если |S_t/5₂[ =10, то a_Hfl = 0,5 In 10 = 1,15; = lg 10 = 1. Таким образом, 1Б = 1,15Нп,

1 Нп = 0,868 Б = 8,68 дБ.

§ 4.11 Уравнения четырехполюсника, записанные через гипербо­лические функции. Для симметричного четырехполюсника Л-форму уравнений (4.1) и (4.2) записывают иногда через гиперболические функ­ции от аргумента g, полагая А = D = chg, Z? = Z_cshg, С = shg/Z_c. При этом AD- ВС = ch²g-sh²g = l и

U_} = chgt/₂ +Z_C shg /₂;

/,=^-C/,₊chg/₂. (4.50)

Убедимся в справедливости замены А на chg:

e^g - А + yjВС, е'^х =--------- 7==^; ch g = — (e^g + е ^g) = А

A + yjBC 2

Форму записи через гиперболические функции используют, например, в теории фильтров (см. гл. 5).

Для несимметричного четырехполюсника уравнения через гиперболические функции запишем следующим образом:

С¹) — ^/Z_C[ / Z_c2 ch Г (j f + •JZci Z_c2 sh Г /₂,

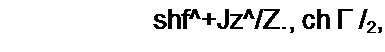где Г—мера передачи, ch Г = yU D: sh Г =

Если несимметричный взаимный четырехполюсник нагружен на Z_c2, то U₂ = /₂ Z_c2; 6’1 = б’₂ АыАз (ch С - sh Г) и /, = /₂ ^/z_c2 /Zcj (ch Г + sh Г). Имея в виду, что е^г = ch Г + sh Г, получим

A ^/zc2^еГ’ А = 4 Аз А^еГ-

Мерз передачи Г = а' + j b’ = Inf^T/Tb' + ^8С). Если четырехполюсник симметричный, то Z_c( = Z_c2 Z) = Л Г = g. Так как _>/Z_c( /Z_c2 = J А/ D, то передача по напряжению для несимметричного взаимного четырехполюсника, нагруженного на Z_c2, составляет 1ft =“ = 1н — + 1п(-^AD * -/вС) и передача по току In = In ~ + In + ^ВС).

U1 и А

§ 4.12 Конвертор и инвертор сопротивления. Если у невзаимного четырехполюсника В ~ С =0 и он нагружен на зажимах pq на сопротив­ление Z_H, то входное сопротивление со стороны зажимов шп

2 - Л _ ^н_

^8Х С Z_H + D А) ’

где = D/ А, т. е. четырехполюсник преобразует (конвертирует) сопро­тивление Z_K в сопротивление Z_H / к_}. Коэффициент называют коэф­фициентом конвертирования. Если А и D имеют одинаковые знаки, то Z_ax имеет тот же знак, что и Z„ (конвертор положительного сопротив­ления), если разные, то знак Z_BX противоположен знак}' Z_H (конвертор отрицательного сопротивления).

Если у конвертора А ~ 1, то k_} = D\ = k_} /₂- $ этом слу­

чае конвертор называют идеальным конвертором с преобразованием тока (при неизменном напряжении).

Если у конвертора D = 1, то к_} - 1/ Л; Ц = G₂ Ai; А = /3. Такой кон­вертор называют идеальным конвертором с преобразованием напряже­ния.

У конвертора есть Н- и (7-матрицы, но отсутствуют Z- и /-матрицы.

Если у невзаимного четырехполюсника А = D = 0, то Z_BX = В/(С Z„) и четырехполюсник называют инвертором сопротивления, а 5/С ~ к₂ — коэффициентом инвертирования.

Если В и С имеют одинаковые знаки, то Z_ex = \/ Z_H (инвертор поло­жительного сопротивления), если знаки у В и С разные, то Z_8X = -1/Z_H (инвертор отрицательного сопротивления).

У идеального инвертора входное сопротивление не зависит от того, к каким зажимам (pq или тп) подключена нагрузка.

У инвертора есть У- и Z-матрицы, но отсутствуют Н- и G-матрицы.

§ 4.13 Гиратор. Гиратором называют инвертор положительного со­противления, имеющий следующую /-матрицу:

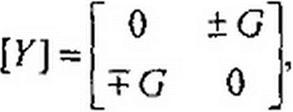
где G — проводимость гиратора. Для идеального гиратора G — веще­ственное число. Для гиратора /, = G(A; /₂ = -G

Гиратор не поглощает энергию. Он преобразует напряжение в ток. Если на выходе гиратора включено сопротивление Z₄, то его входное сопротивление Z_BX =1/(G²Z_H).

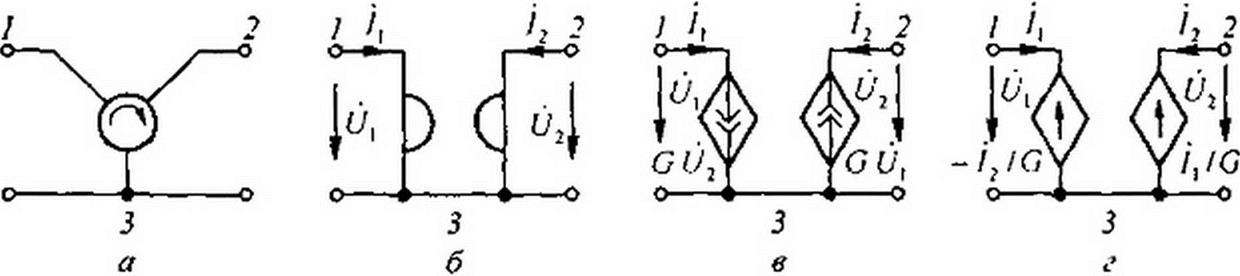
Рис. 4.8

Представим гиратор как трехполюсник (зажим 3 на рис. 4.8, а — общий для входной и выходной цепей). Его /-матрица остается неизмен­ной, если, оставив гиратор неподвижным, в направлении стрелки после­довательно изменять нумерацию его зажимов. Гиратор является невзаим­
ным (необратимым) четырехполюсником, так как для него У₎₂ * Х_2|. В настоящее время гиратор чаще обозначают в соответствии с рис. 4.8, б.

Практически осуществить гиратор можно, например, по схеме (рис. 4.8, в}, в которой использованы два управляемых напряжением ис­точника тока: G 0₂ ^и G й\> или по схеме (рис. 4.8, г) с двумя управля­емыми источниками напряжения. Воспользовавшись табл. 4.1, можно перейти от Х-параметров гиратора к его Z- и Л-парамстрам:

§ 4.14 Операционный усилитель. Операционный усилитель (ОУ) — это усилитель с очень большим входным сопротивлением, очень малым выходным сопротивлением и очень большим коэффициентом усиления £ (теоретически Л-»оо, практически к « I О'¹ + I (г). ОУ выполняют по интегральной технологии в виде отдельного кристалла, поэтому его мож­но считать самостоятельным активным элементом схем, подобно тран­зистору. Коэффициент усиления к = /(1 + у сот). Знак минус обуслов­

лен тем, что вход I является инвертирующим. Постоянная времени т учитывает инерционные свойства ОУ.

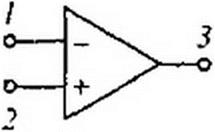
ОУ имеет обычно восемь выводов: два входных, или управляющих, один выходной (3), один заземленный (<7), два вывода для источника пи­тания и два для регулировки. Четыре последних вывода на схемах не показывают. На электрических схемах ОУ изображают в виде треуголь-

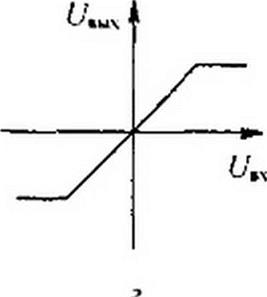Рис. 4.9

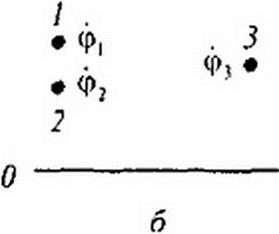
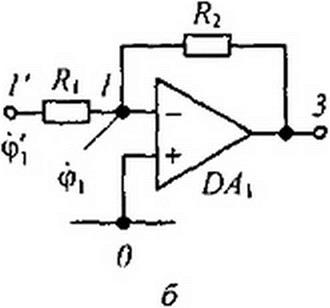
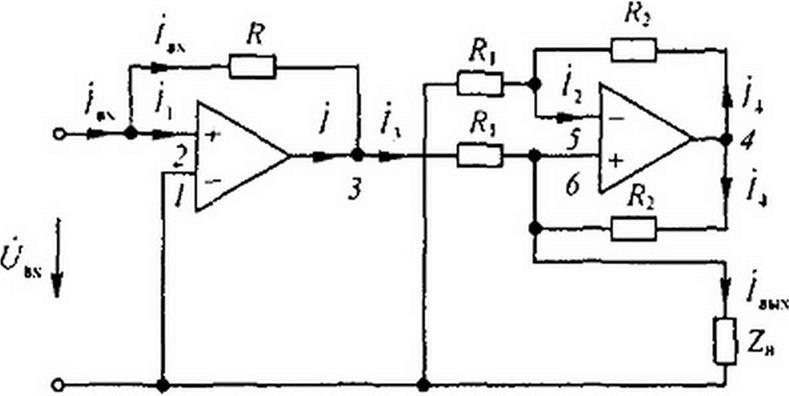
ника с тремя выводами /, 2, 3 (рис. 4.9, а), потенциалы которых относи­тельно заземленной точки соответственно <p_h ф₂, ф₃ (рис. 4.9, б). При включении ОУ по дифференциальной схеме его входное напряжение 1/_вх - ф, -ф₂. При использовании одного входа и заземлении второго (7_ЙХ = ф|. Выходное напряжение ОУ равно разности потенциалов между точкой 3 и заземленной точкой 0: {/_вых - ф₃ -0 = ф₃, оно в к раз больше входного, т. е. к (ф, - ф₂) = ф_} или £ф₍-ф₃ соответственно. Значение коэффициента усиления к записывают рядом с ОУ либо внутри его. Зна­
ние числового значения к при анализе схем с ОУ не всегда требуется, важ­но, что к велико и стремится к бесконечности. Так как к ->оо, а (/_ВЬ|Х - величина конечная, то в зависимости от способов включения (Ф_т - Ф₂ ) -> О ИЛИ (р| —> 0.

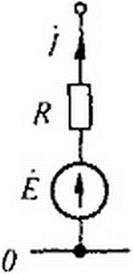
Таким образом, входные напряжения ОУ можно полагать в первом приближении равными нулю. Для облегчения анализа схем, содержащих ОУ, последние в ряде случаев будем заменять их расчетными эквивален­тами. Выходную цепь ОУ будем заменять ветвью (рис. 4.9, в), присоеди­ненной между выходной точкой 3 и заземленной точкой 0 и содержащей источник ЭДС £ = А: (ф) -ф₂) ^или £ = * Ф|» соответственно, и последо­вательно с ним включенным сопротивлением порядка десятков или со­тен Ом (точное числовое значение его обычно не задано), по которой проходит некоторый ток / (рис. 4.9, в). Значение тока / в расчетах, как правило, не требуется, а если и потребуется, то всегда может быть опре­делено по законам Кирхгофа. Входное сопротивление ОУ в первом при­ближении полагают стремящимся к бесконечности.

После замены входной и выходной цепей ОУ на расчетные эквивален­ты схему рассчитывают по законам Кирхгофа, имея в виду в первом при­ближении, что входные напряжения и входные токи всех ОУ равны нулю.

Расчет схем с операционными усилителями, когда необходимо учесть конечное (не бесконечное) значение к и конечное значение входных со­противлений, производят обычно методом узловых потенциалов.

Зависимость м_вых -/(w_BX) для ОУ линейна только до некоторого максимального значения м_вь1Х * 10-е-15 В, после чего наступает насыще­ние. В дальнейшем будем полагать, что работа схем с ОУ происходит на линейном участке характеристики ОУ (рис. 4.9, г). Заметим еще, что ско­рость изменения выходного напряжения г?«_вых / di у ОУ ограничена ве­личиной порядка 10⁶ В/с. В последнее время минусовый вход ОУ обо­значают кружком, как на рис. 4.10, а.

Рассмотрим три примера.

Сначала рассмотрим схему (рис. 4.10. б), являющуюся схемой источника напряжения, управляемого напряжением. Резисторы R_} и могут регулироваться. Через резистор /?₂ осуществляется обратная связь. Расчетная схема изображена на рис. 4.10, в. Так как вто­рой вход схемы (рис. 4.10. б) заземлен (ф₂ = 0К ^а напряжение на входе ОУ должно быть равно нулю, то ф) * 0.

Потенциал на входе схемы ф! = -//?(. Потенциал на выходе ОУ ф« =//?₂. отсюда

Так как то выходное сопротивление схемы стремится к нулю,

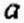т. е. действительно схема на рис. 4.10, б может выполнять функции источника напряже­ния (внутреннее сопротивление которого стремится к нулю), управляемого напряжением.

Рассмотрим схему преобразователя сопротивлений на ОУ, изображенную на рис. 4. Н, а. В схеме имеется два ОУ и пять сопротивлений Z_t - Z₅. Покажем, что вход­ное сопротивление схемы относительно зажимов АВ для малых переменных составляю­щих Z_Afj = Z₂Z_A. Обозначим токи в ветвях в соответствии с рис. 4.11, а. На

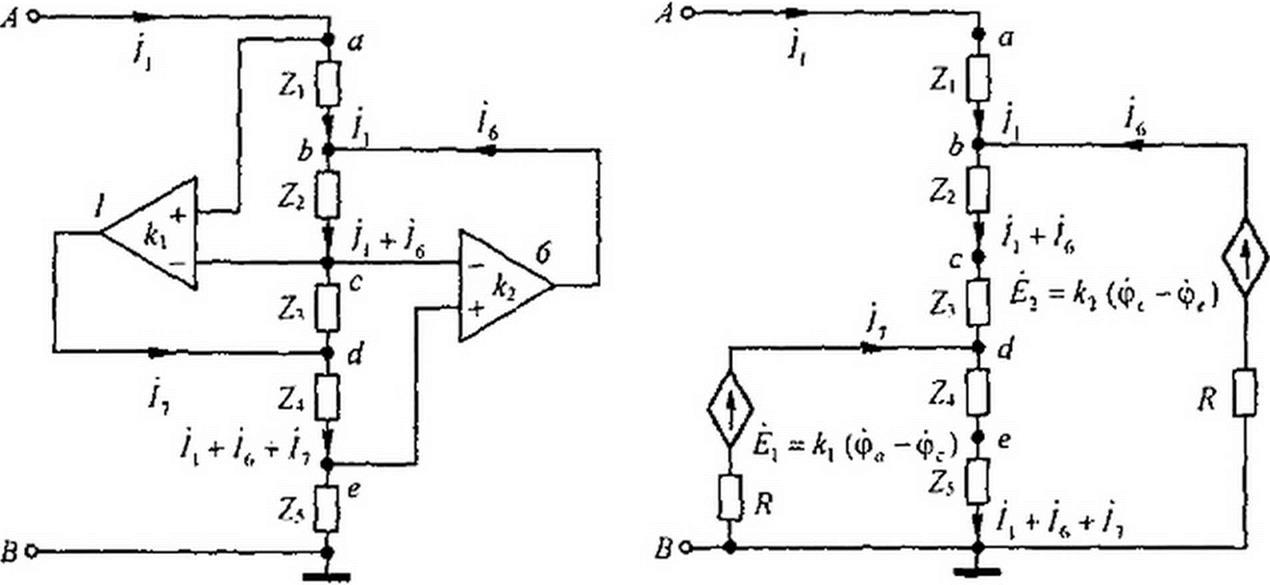
Рис. 4.1 ]

рис. 4.11,6 изображена схема, в которой выходные цепи ОУ заменены их расчетными эк­вивалентами. Для схемы рис. 4.11, б приравняем к нулю входные напряжения ОУ:

<>_Bxi = +(А +Л)2₂=0; (4.51)

6'_ах2 =Фс =(/( + /₆)2₃ •»•(/, + /₆ +Л)²4 =° (4.52)

Из (4.51)

А + 4 = “А (4.53)

^■2

7, Z

Из (4.52) с учетом (4.53) получим !_} + /_ь + /₇ = _ ¹ J . Так как U^. + t)_tV =0, то

Z₂ Z л

входное напряжение схемы

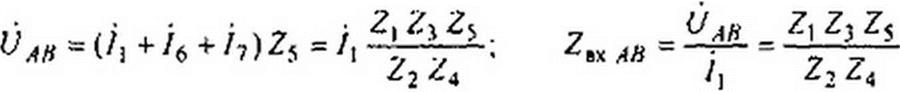
Применение ОУ для реализации гиратора иллюстрирует рис. 4.12. В этой схеме три ОУ и четыре резистора. Проводимости резисторов ft_} н Л₂ выполняют функции прово­димостей гиратора. Обозначим потенциалы узлов и токи ветвей в соответствии с рис. 4.12. Учтем, что напряжение и токи на входе каждого ОУ стремятся к нулю, а точки, обозна­ченные цифрой 0, и точка С практически имеют нулевой потенциал. В этой схеме ток /4 = t'_ej4X//?, потенциал точки / <р; = -Ц R = -U_aux. Потенциал точки С

Ф(’ — 0 — ф| — Ij /Jj .

Отсюда /j = ф] //?2 = -(/_аых //?₂. Но А⁼~/3’ поэтому

(4.54)

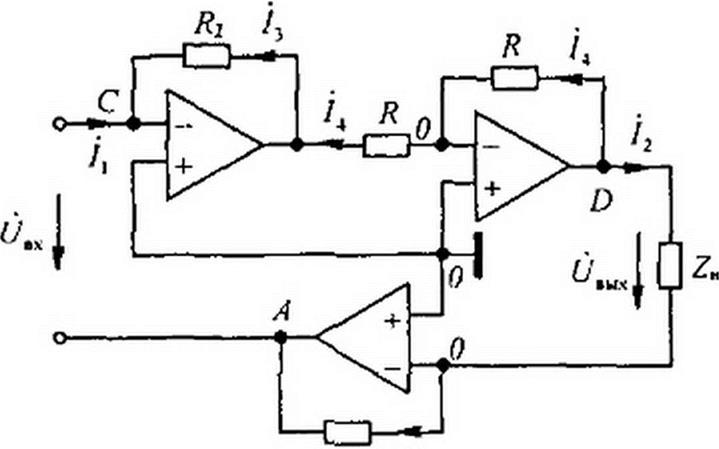
i₂

Рис. 4.12

Потенциал точки А ф_л = -i₂ R_t. Входное напряжение

(4.55)

Имея в виду, что для У-формы записи уравнений четырехполюсника ток /₂ должен иметь направление, противоположное указанному на рис. 4.12. установим, что уравнение (4.54) и (4.55) являются уравнением гиратора. Недостатком схемы на рис. 4.12 является то, что источник сигнала и нагрузка Z_H непосредственно не соединены с заземленной точ­кой.

§ 4.15. Управляемые источники напряжения (тока). Управляемый источник напряжения (тока) представляет собой невзаимный четырех­полюсник (трехполюсник), выходное напряжение (ток) которого пропор­ционально входному напряжению (току) этого четырехполюсника, а сам он обладает свойством источника напряжения (ЭДС) (напряжение на его зажимах не зависит от протекающего через него тока) или источника тока (его ток не зависит от нагрузки). Управляемый источник обозначают ча­сто в виде ромба, в котором указана стрелка (если это источник напря­жения), либо двойная стрелка (если это источник тока). Рядом записы­вают управляющую величину, умноженную на некоторый масштабный множитель. Управляющими величинами могут быть также интеграл и производная по времени от тока или напряжения.

Известны четыре типа идеализированных управляемых источников:

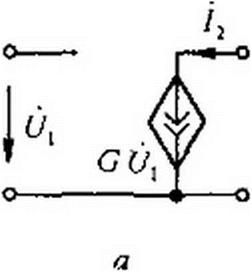
1) источник тока, управляемый напряжением (ИТУН). Схема его изображена на рис. 4.13, а, Входной ток 1_} = 0, выходной ток пропорци­онален входному напряжению: /₂ = G входное и выходное сопротив­ления бесконечно велики. Матрица У ИТУН такова:

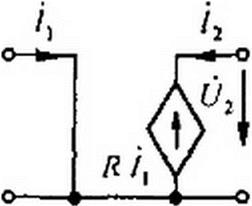
2) источник напряжения, управляемый током (ИНУТ). Схема его представлена на рис. 4.13, б. Входное напряжение =0, выходное

напряжение пропорционально входному току: (У₂ входное и выходное сопротивления равны нулю. Его Z-матрица имеет вид:

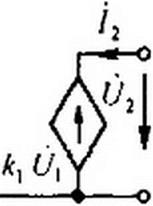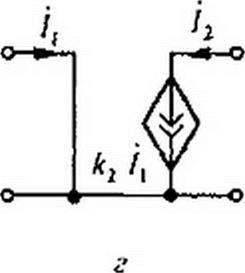Рис. 4.13

3) источник напряжения, управляемый напряжением (ИНУН). Схе­ма дана на рис. 4.13, в. Входной ток =0, выходное напряжение про­порционально входному: й₂ = А| Ц, входное сопротивление бесконечно велико, а выходное равно нулю. Его G-матрица такова:

4) 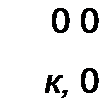источник тока, управляемый током (ИТУТ). Схема изображена на рис. 4.13, г. Входное напряжение Ц =0. выходной ток пропорционален входному: /₂ =А₂ Д, входное сопротивление равно нулю, выходное — бесконечности. Матрица //-параметров его равна

Каскадное соединение ИНУТ с ИТУН обладает свойством ИТУТ, а каскадное соединение ИТУН с ИНУТ — свойством ИНУН.

Для всех перечисленных управляемых источников выходная величи­на не влияет на входную, а входная мощность равна нулю, так как вход­ной ток либо входное напряжение равны нулю.

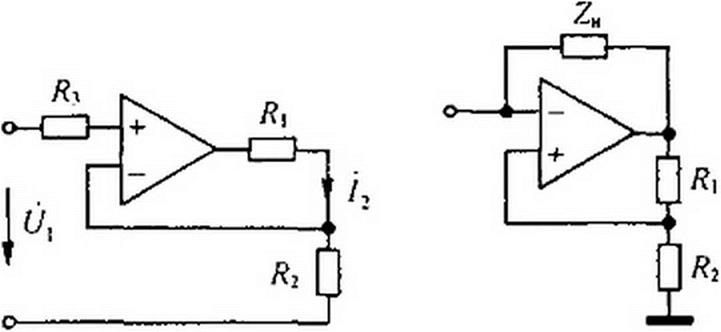
Управляемые источники часто осуществляют на основе операционных усилителей. Так, схема ИТУТ на двух ОУ — на рис. 4.14.

Убедимся, что схема на рис. 4.14 обладает свойствами ИТУТ. Воспользуемся обозна­чениями на этой схеме.

Входное напряжение первого ОУ равно нулю, =0. <р₂ = 0. Входной ток первого ОУ д =0. входной ток второго ОУ /₂=0. Входной ток схемы /_вх = -ф₃//?, отсюда Фз = -/_ex R. Выходной ток первого ОУ обозначим /, Тогда для узла 3 по первому закону Кирхгофа /₃ = /_и + /. Так как /₂ = 0, то

(4.56)

• • •

а потенциал точки 6 ср$ = q>j -/3 /?] =<₽з -(/_рч ⁴ О#|. Входное напряжение второго ОУ
равно нулю, поэтому ф₅ =ф₆. Так как сопротивление между точками 4 и 5 равно сопро­тивлению между точками 4 и б, то

■ ₌ Ф, ₌ ■>,*/„ Л+ (/„+/)/?,
Л₂ я₂

Приравняв (4.56) к (4.57), определим

Ф₄ =-—(4(Я + Я₁)(Я,+/?,)-/Л₁(Л_]+Я₂)). (4.58)

К]

Подставим (4.58) в (4.56)

(4.59)

Для узла 6, по первому закону Кирхгофа,

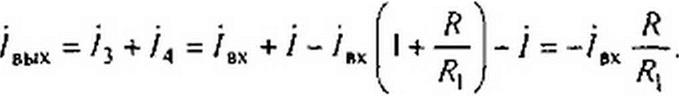Так как /_вых пропорционально /_вх, (/_вх - 0, а выходной ток /_вых не зависит от сопротивления нагрузки Z_H, то схема рис. 4.14 по отношению к выходной цепи обладает свойствами источника тока, управляемого током /_вх. На рис. 4.15. а представ-

б в

Рис. 4.15

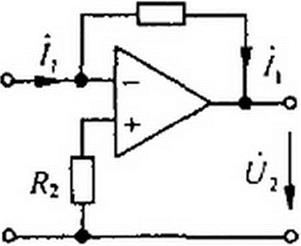
лена одна из возможных схем ИНУТ (й₂ = Я, /₍). на рис 4.15. б — одна из возможных схем ИНУН, а на рис. 4.15, в — схема конвертора отрицательного сопротивления (Z_ax - -Z_H R₂ 1Я,).

Как имитировать элементы Я. С, заземленную и незаземленную L, частотно зависи­мые сопротивления, высокоомные резисторы — см. приложение П2.

В § 4.14-4.15 было принято, что для ОУ К ----------- ------------------------------------------------------------------------------ ------------------------------------------------------------------------------- > да за счет того, что А_о —► да.

. , -2-1 ^{1 +}

Практически же А_о * 10 -5-10°, а т* 10 +10 . Поэтому при относительно высоких ча­стотах со при рассмотрении схем с управляемыми источниками следует учитывать зави­симость АГ от со.

§ 4.16. Активный четырехполюсник. Под активным четырехполюс­ником будем понимать линейный четырехполюсник, содержащий источ­ники энергии, за счет которых на разомкнутых зажимах его появляется напряжение. Следует иметь в виду, что в понятие «активный четырехпо­люсник» в литературе вкладывают также и иной смысл, а именно — такой четырехполюсник, активная мощность на выходе которого превы­шает (может превышать) активную мощность на входе. Этот эффект
достигается обычно за счет того, что в состав четырехполюсника входят активные невзаимные элементы, такие, как операционные усилители, транзисторы, электронные лампы, туннельные диоды и др. Чтобы раз­личать эти два класса активных четырехполюсников, условимся рассмат­риваемый четырехполюсник называть активным автономным (по зажимам тп и (или) pq), а четырехполюсник, обладающий свойством усиливать мощность, — активным неавтономным в направлении усиле­ния мощности.

Рассмотрим уравнения, описывающие связь между входными и вы­ходными величинами активного автономного четырехполюсника и его схему замещения.

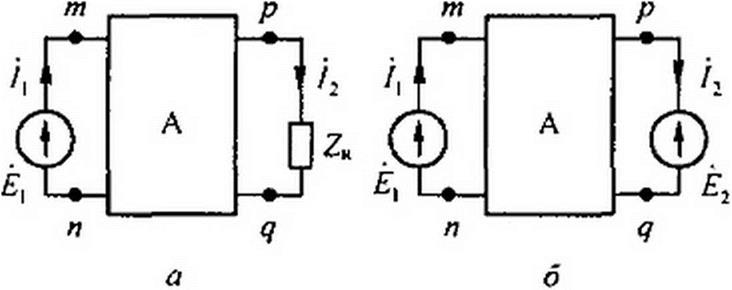
Положим, что в первой ветви тп активного четырехполюсника (рис. 4.16, а) есть источник ЭДС £_|} во второй ветви pq — нагрузка Z_H, а в остальных ветвях (3-р), находящихся внутри четырехполюсника,

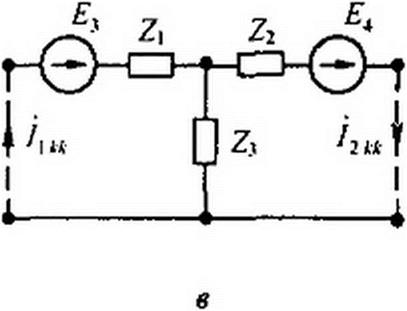имеются или могут иметься источники ЭДС Ё_к (индекс к может прини­мать значения от 3 до р). Тогда, заменив по теореме компенсации сопро­тивление Z_H на источник ЭДС £₂ (рис. 4.16, б), запишем выражения для токов и /₂:

р .

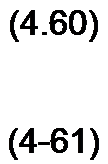- £\ У|| - ^2 Т12 ⁺ 2Z Тц,

*=3 Р .

/₂ = £| у₂| “ ^2 У 22 ⁺ zZ У2к-

к=3

Осуществим короткое замыкание одновременно на^зажимах тп и pq. При этом по первой ветви будет протекать ток /|_К = ^Ё_к у_}к, а по вто­рой — ток 1_1к = ^Ё_ку_2к.

Л=3 Р Р .

В (4.60) вместо ^Е_к у_]к, подставим /_и, а в (4.61) вместо ^Ё_ку_2к подставим /_2к. Кроме того, заменим £, на (7, и £₂ на U₂. В результа­те получим

• • • •

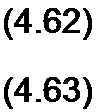Л “ Ёк ⁼ У\\У\ “Zl2 ^2’

Г • * •

^2 “ Ьк ⁼ У2\^\ ~~ У22 ^2-

Уравнения (4.62) и (4.63) отличаются от уравнений (4.14) и (4.15) толь­ко тем, что в их левых частях находятся соответственно - /_I(t и /₂ - hk вместо jj и Л. Отсюда следует, что все уравнения, получающиеся из (4.14) и (4.15) в результате их преобразований, справедливы и для актив­ного четырехполюсника, только в них Д следует заменить на 1_} -7_И, а /₂ — на /₂ - Так, Я-форме уравнений пассивного четырехполюсни­ка (Ц = А й₂ + В /₂, /| = С U₂ + D /₂) соответствует Л-форма уравнений активного четырехполюсника:

(7₁=Л(7₂+5(/₂-/_и);

А “ Ёк = С ^2 ⁺ £* (^2 " ^2*)’

Коэффициенты Л, В, С активного автономного взаимного четырехпо­люсника удовлетворяют условию Л О - ВС = 1 и определяют их так же, как и для пассивного.

На рис. 4.16, в изображена одна из возможных Т-схем замещения активного четырехполюсника. Сопротивления Z₍, Z₂ и Z₃ находят че­рез коэффициенты Л, В, С, так же как для пассивного четырехполюсни­ка, а ЭДС £₃ и Ё₄ вычисляют по значениям токов /_]Л и [_2к и сопро­тивлениям из уравнений, составленных для режима одновременного ко­роткого замыкания входа и выхода (показано штриховой линией на рис. 4.16, в):

Ёк (^1 ⁺ ^.0 “ hk ⁼

“ Аа ^3 ⁺ Ьк (?2 ⁺

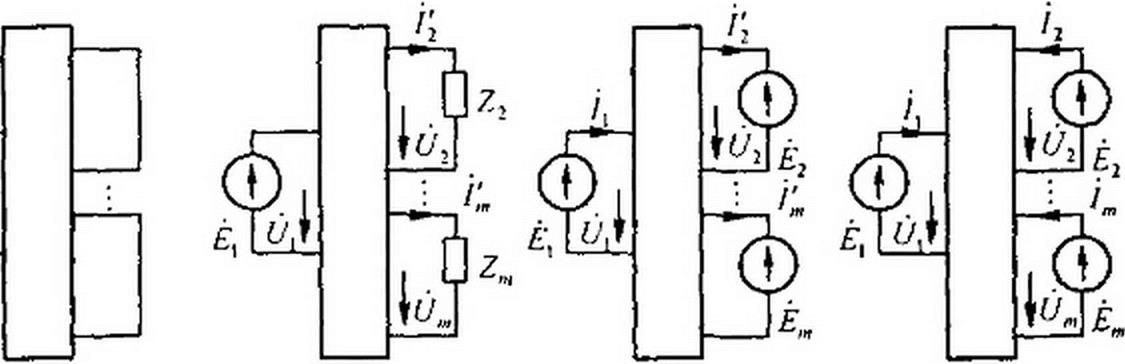
§ 4.17 Многополюсник. На рис. 4.17, а изображена пассивная схема, в которой вы­делено т ветвей (гп пар зажимов). Условимся называть такую схему многополюсником. Будем полагать известными входные у_п - у_тт и взаимные у„,_к проводимости вет­вей. Они определены в соответствии с § 2.15 (А-ветвь входит только в А-контур; направле­ния всех контурных токов при составлении уравнений по методу контурных токов одина­ковы).

Включим в ветвь I ЭДС Е, = Ц. а в ветви 2~т нагрузки Z₂-Z„, (рис. 4.17, б). Токи в ветвях 2-т обозначим Л . а в ветви / обозначим Все токи направлены по часо­вой стрелке.

а б в

Рис. 4.17

На основании теоремы компенсации заменим нагрузки Z₂-Z„ на источники ЭДС Е_г-Е_т, направленные встречно токам Г₂-1'_т (рис. 4.17, в). На основании принципа наложения запишем выражения для токов ветвей:

Л ~Ц Ун >'i2 ^_ >'□ “••• ~й_т>’|_т;
Л ⁼ ^\У2\ "(7₂ >22 ^- (^J'₃ y_2J ~ У2т>

(4.64)

т ~ \ Ут\ ^2Ут2 U ) УтЗ ~ т Утт

Изменим направления токов в ветвях 2~т на противоположные и назовем их токами /₂-/_да йг -~^2> •••• (рис. 4.17, г). Для того чтобы все слагаемые уравнений

имели положительные знаки, введем следующие обозначения: Y_klt = у_кк,

^z i* = ~У\к = 'Ль ^i>_r = = >> = У,₍> (Р * г /1).

Тогда система уравнений многополюсника (4 64) будет иметь вид

(4.65)

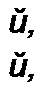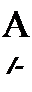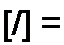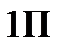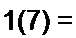m2 .................... тт

Если систему уравнений многополюсника (4.65). записанную в F-форме, решить отно­сительно [U], то получим систему уравнений многополюсника, записанную в Z-форме:

(4.66)

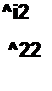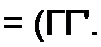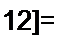Если у многополюсника Y_km * Y_mk, его называют невзаимным. Если многополюсник содержит источники энергии (активный автономный многополюсник), то его уравнения в )- или Z-форме запишутся подобно тому, как это сделано в § 4.16 для четырехполюсника:

т[й]=г-4] или izj(/-/„]=p]

Исследование работы электрических цепей часто проводят графическими методами путем построения круговых и линейных диаграмм Перед тем как приступить к изучению круговых диаграмм, рассмогрим вопрос о построении дуги окружности по хорде и впи­санному углу.