^“^22^21» £-1/.У21’ ~ (У\\У22 ~ У\2 У2]У У1\’ & ~ У|1 У21 • (4-1 8)
В уравнениях (4.16) и (4.17) заменим Ёх на и £2 на IJ1 и, воспользовавшись обозначением (4.18), получим уравнения в Л-форме
Ц = лй2+Я/2;
/, = сй2 +d!2.
Проверим выполнение соотношения (4.13) для взаимного четырехполюсника:
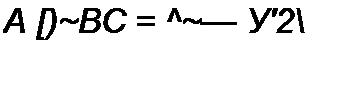 | |||
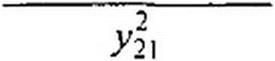 | |||
|
Для невзаимного четырехполюсника
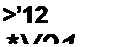 и A D- ВС = у)2! У2\ * I-
и A D- ВС = у)2! У2\ * I-
Рассмотрим соотношения, которые имеют место между й} и /, и й2 и /2, если источник ЭДС £, присоединен к зажимам pq, а нагрузка — к зажимам тп (рис. 4.3, а).
 | |||
 | |||
| |||
| |||
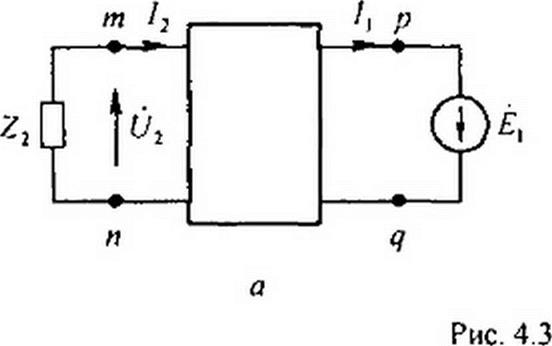 |
Как и в предыдущем выводе, заменим нагрузку Z2 ка источник ЭДС с ЭДС £2, направленный встречно току /2, и запишем выражения для токов У, и /2:
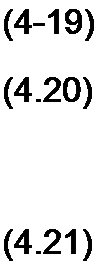 | |||||||||||||||||||||||||
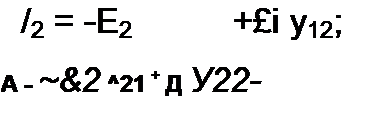 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
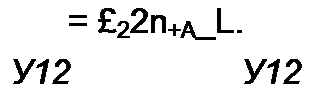 | |||||||||||||||||||||||||
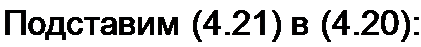 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
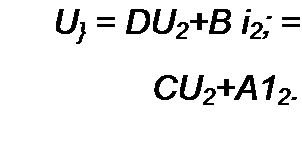 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
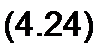 | |||||||||||||||||||||||||
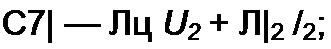 | |||||||||||||||||||||||||
 | |||||||||||||||||||||||||
|
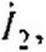 | |||
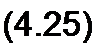 | |||
где Л| । ~ А', Л|2 — В', Л2] — С; А22 — D.
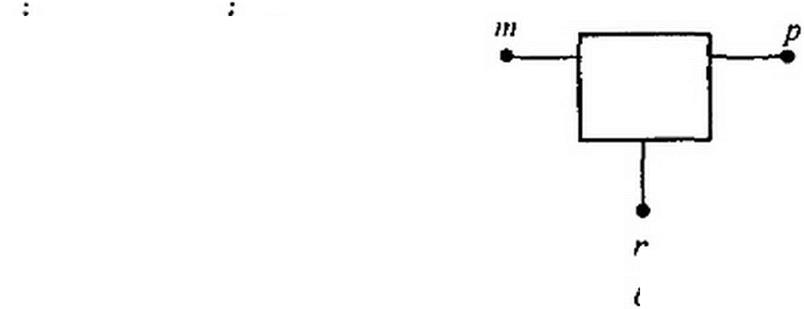
Частный случай четырехполюсника, у которого зажимы п и q схемы рис. 4.3, б имеют одинаковый потенциал (например, когда оба они соединены с заземленной точкой схемы), называют трехполюсником. Изображение трехполюсника показано на рис. 4.3, б.
Если в четырехполюснике отсутствует общая для входа и выхода точка, то такой четырехполюсник также можно рассматривать как трехпо- люсник, если схема внутренних соединений его окажется симметричной относительно мысленно проведенной посередине четырехполюсника горизонтальной линии (она и будет общим для входа и выхода «зажимом»).
§ 4.4 Определение коэффициентов /4-формы записи уравнений четырехполюсника. Комплексные коэффициенты А, В, С, D, входящие в уравнения (4.1) и (4.2), можно определить по формулам (4.18), если схема внутренних соединений четырехполюсника и ее параметры известны,
либо используя входные сопротивления четырехполюсника, полученные опытным или расчетным путем.
Комплексные входные сопротивления находят опытным путем с помощью ваттметра, амперметра и вольтметра по схеме, подобной схеме на рис. 3.24, а, с тем отличием, что вместо двухполюсника к зажимам тп и pq (в зависимости от определяемого входного сопротивления) подключают испытуемый четырехполюсник.
Определим комплексное входное сопротивление четырехполюсника при трех различных режимах его работы.
1. При питании со стороны зажимов тп и разомкнутой ветви pq (/2 = 0, индекс «х»):
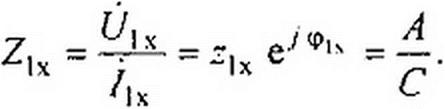 | |||
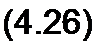 | |||
2. При питании со стороны зажимов тп и коротком замыкании ветви pq (О2 —0, индекс «к»):
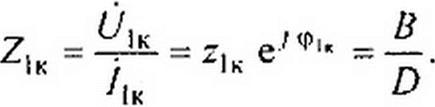 | |||
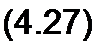 | |||
3. При питании со стороны зажимов pq и коротком замыкании зажимов тп ((?2 - 0):
(4.28)
Таким образом, для определения четырех неизвестных коэффициентов А, В, C,D взаимного четырехполюсника располагаем четырьмя уравнениями: AD-BC~\, Z}*=A!C', ZXk~B/D\ Zlk=B/A. Составим разность
L или = JL. (4.29)
Z|X AD AD 21X AD
Имеем
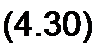 Z2k/Z1k = £>/A
Z2k/Z1k = £>/A
Умножим (4.29) на (4.30):
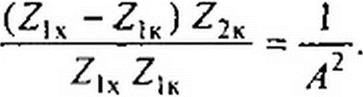 | |||||||
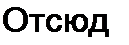 | |||||||
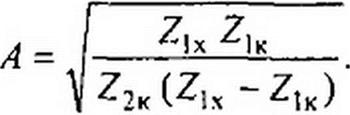 | |||||||
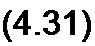 | |||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
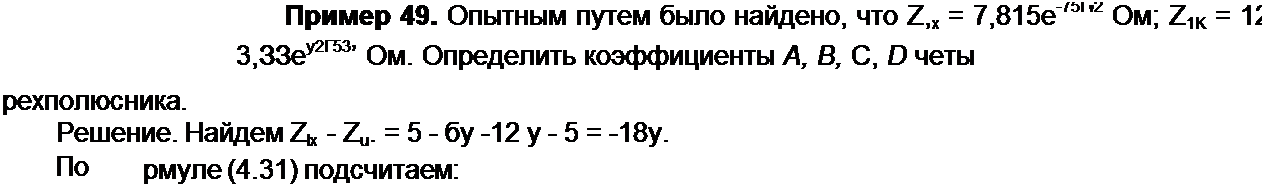 | |||||||||||||
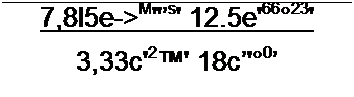 | |||||||||||||
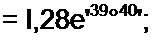 | |||||||||||||
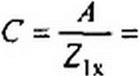 | |||||||||||||
|
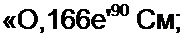 |
B=AZ2k = 4,2бе'67 Ом;
D = B/Z,K =0.34.
Пример 50. К зажимам pq (рис. 4.1) четырехполюсника примера 49 подсоединена нагрузка 22=6 + убОм; к зажимам тп—источник ЭЛС. Найти Ц и если /2 = I А.
Р е ш е н и с. По формуле (4.1)
t/; = AU, + В/2 = (AZ, + £) = Ь(1.28е/4S<>-бУ! e?45°+4,26е'бГ>) = 14,85 e7’9*45' 8.
По формуле (4.2)
Zt =С(У2+£)/2 =/2 (C Z2 + £>) = IJ65eyl23’A.
§ 4.5. T- и П-схемы замещения пассивного четырехполюсника. Функции пассивного взаимного четырехполюсника как передаточного звена между источником питания и нагрузкой может выполнять Т-схема (схема звезды рис. 4.4, а) или эквивалентная ей П-схема треугольника (рис. 4.4, б).
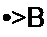 Предполагается, что частота со фиксирована. Три сопротивления Т- или П-схемы подсчитывают с учетом того, что схема замещения должна обладать теми же коэффициентами А, В, С, D, что и заменяемый ею четырехполюсник.
Предполагается, что частота со фиксирована. Три сопротивления Т- или П-схемы подсчитывают с учетом того, что схема замещения должна обладать теми же коэффициентами А, В, С, D, что и заменяемый ею четырехполюсник.
рмулах (4.31) и (4.32) перед корнем взят знак плюс. Этому знаку соответствует
отсчет й2 и /, по рис. 4.2. а. Знак минус перед корнем огброшен. так как он соответствует отсчету 02 и /2 и в противоположном направлении.
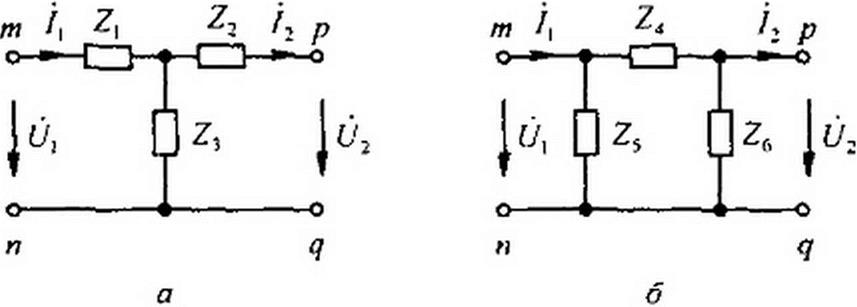 |
|
Задача эта однозначна, так как схема замещения содержит три элемента и четырехполюсник характеризуется тоже тремя параметрами (одна связь между А, В, С, D задана уравнением A D - В С - I )*>.
Выразим напряжение и ток /( Т-схемы (рис. 4.4, а) через напряжение 02 и ток /2:
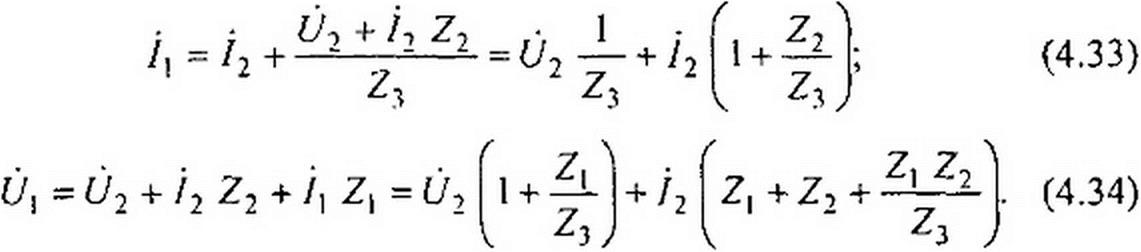 |
|
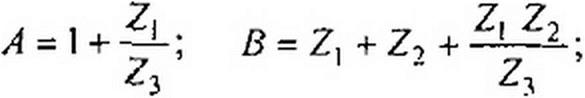 | |||
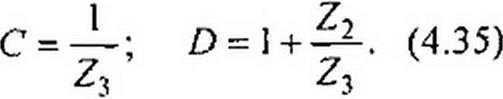 | |||
Следовательно,
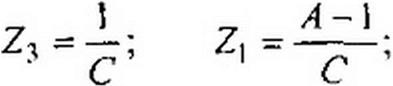 | 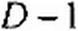 | ||||||||
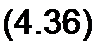 | |||||||||
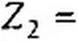 | |||||||||
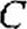 | |||||||||
Формулы (4.36) позволяют определить сопротивления Z]t Z2 и (рис. 4.4, а) по коэффициентам четырехполюсника Я, С, D. Аналогичные выкладки для П-схемы (рис. 4.4, 6) дают:
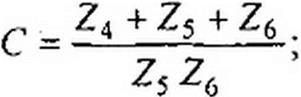 | |||||
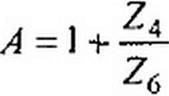 | |||||
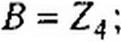 | |||||
|
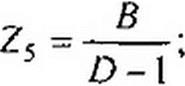
|
(4.38)
(4.39) (4.40)
______________________ А -1
*' У невзаимного четырехполюсника у)2 * поэтому для него схема замещения образована не тремя, а четырьмя элементами (см., например, схему замещения транзистора в § 13.35).
Если четырехполюсник симметричный, то А = D ив Т-схеме замещения Z, = Z2, а в П-схеме Z5 = Z6.
§ 4,6. Определение коэффициентов К, Z-, G- и //-форм записи уравнений четырехполюсника. Комплексные коэффициенты Уц, У12,
У2|, У22 в уравнениях (4.3) и (4.4) найдем следующим образом: Уп = /, /Ц при С/2 = 0; У)2 = /) /(/2 при U, -- 0; У22 - 12/02 при Ц = 0. Обозначим У22 = Ут ™ K!2=“Zi2 и r2i^ “^21-
Коэффициенты Z|t, Z)2, Z2], Z22 в уравнениях (4.5) и (4.6) определим так: Z1}=U}/li при /2=0; Zl2=t/2//] при /2-0; Z22=U2112 при = 0.
Аналогичным образом определим коэффициенты и других форм записи, например //-формы: Л/() =Ц/7) при й2 = 0; H22-I2IU2 при /| = 0; Н2[ - Л / /| при й2 - 0. Обратим внимание на то, что для взаимного четырехполюсника Yl2=Y2h Z)2=Z2I, но Gj2 =-62]’ а ^12 не равно В21 даже по модулю.
Пример 51. Вывести формулы Z-параметров для Т-схемы замещения четырехполюсника (рис. 4.4, а).
Решение. Для Т-схемы замещения
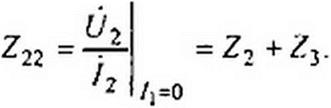 | |||||
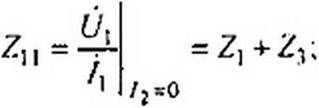 | 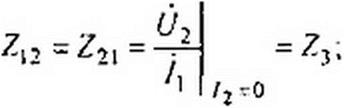 | ||||
§ 4.7 Определение коэффициентов одной формы уравнений через коэффициенты другой формы. На практике возникает потребность в переходе от одной формы записи уравнений к другой.
Для того чтобы коэффициенты одной формы записи найти через коэффициенты другой формы, необходимо выразить какие-либо две одинаковые величины в этих двух формах и сопоставить их, учтя направления токов /[ и /, в них.
Для Л-формы
Ц=/.7-Л^; (4-4|>
02 = А — - Л (4-42)
для Z-формы
Ц=А Zli+/2Z22; (4.43)
U2 = /, Z2] + /2 Z22. (4.44)
Сопоставляя правые части (4.41) и (4.43) и учитывая, что ток /2 в выражении (4.43) равен току - /2 в выражении (4.41), получим
/Н=л/С, Zl2=l/C.
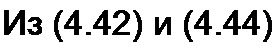 | |||||||
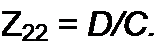 | |||||||
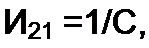 | |||||||
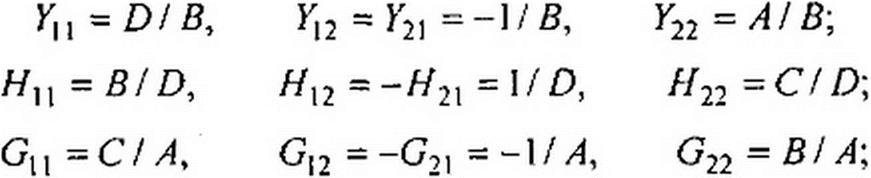 | |||||||
| ||||
| ||||
Пример 52. Определить Г-параметры четырехполюсника через Z-параметры.
Решение. Решим уравнения (4.5) и (4.6) относительно f} и /2, сопоставим полученные уравнения с уравнениями (4.3) и (4.4) В результате получим
) I1 = ^22 / Д 2 ’» — Z] । / Д2 ♦ ^12 = ^21 3 “^12 &7. ’ &7. ~ У~\ I ^-22 “ ^12'
Для Т-схемы (рис. 4.4. а)
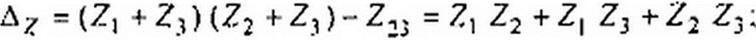 |
|
В табл. 4.1 даны соотношения для перехода от одной формы уравнений к любой другой.
§ 4.8 Применение различных форм записи уравнений четырехполюсника. Соединения четырехполюсника. Условия регулярности. Ту или иную форму записи уравнений применяют, исходя из соображений удобства. Так, в теории синтеза цепей (см. § 10.5-10.8) используют обычно У- или Z-форму записи. Параметры транзисторов для малых переменных составляющих (см. § 15.35) дают в У-, или Я-, или Z-форме, так как в этих формах их удобнее определить опытным путем.
При нахождении связи между входными и выходными величинами различным образом соединенных четырехполюсников (при определении коэффициентов эквивалентного четырехполюсника) используют Z-, Н-, G-, У- и Л-формы.
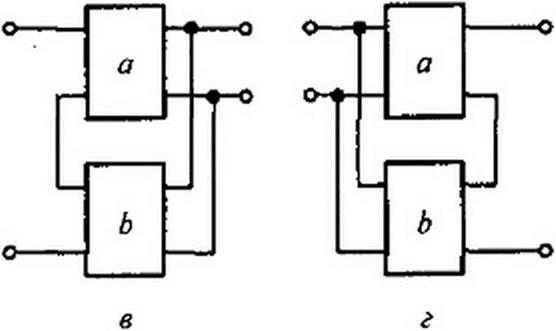
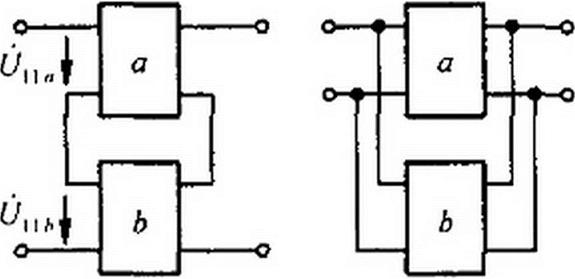
При последовательно-последовательном соединении четырехполюсников а и b (рис. 4.5, а) применяют Z-форму, при параллельно-параллельном соединении (рис. 4.5, б) — К-форму, при последовательно-параллельном (рис. 4.5, в) — Н-форму, при параллельно-последовательном (рис. 4.5, г) — G-форму, при каскадном (рис. 4.5, д) — Л-форму.
Форму записи уравнений выбирают, исходя из удобств получения матрицы составного четырехполюсника. Так, Z-матрица последовательнопоследовательно соединенных четырехполюсников равна сумме Z-мат- риц этих четырехполюсников, так как напряжение на входе (выходе) эквивалентного четырехполюсника равно сумме напряжений на входе (выходе) составляющих его четырехполюсников, а токи, соответственно,
 | |||||
 | |||||
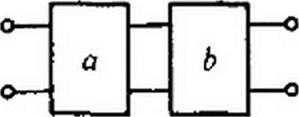 | |||||
Таблица 4.1
| К матрице | От матрицы | ||||
| И | m | (/л | [G] | <■4 A В C D J | |
| и |
| h: "hi | Ду/ Hl2 | 51 |P -ft | - =° |? ? P 9 | A _A C C _l_ D_ C C |
| A}- A, “hi hi | H:2 -w21 I | ||||
| Д] Д) | ^22 /h2 | ||||
| [И | Z22 &7. Л/ ~ ?2\ Az А/ | _L h„ //„ ^21 Д» | I ►9 cj,P J? ta bj „9 1 _ CJI O) •s> I ►-/ Ня/ | D -A В В -1 A_ В В | |
|
| «м е-4 — <ч N N К.| <1 N 7 | _L -hi hl hl hi A, hi h. |
| G22 -G|, | — Л D D -1 С D D |
| Ao- A(; -Gii G„ | |||||
| N и N •и | A,; Au | ||||
| [С] | J_ -zt8 ^11 ^11 ^21 ^Z i | : ^12 *«• tee -hl 1 F„ Г,, Л — — |
| £. — A A A £ A A | |
| A// A/z -Яз. ^ii A// A„ | |||||
| 1 1 Q О со 1________ 1 | •vl — Cl — СЧ r* e> ri <J|N N N r4 r , ~ N 1 N N | -Ka5 -1 te • _ | “A// H w | Q > 0)10) — — 1К/ |
|
| 4 r 4 ^9 . <4 •^чв । » <• <1 . ~ 1 | 3: -I a: —* 1J — ♦J 3: i L* ""Li | ||||
д
Рис. 4.5
на входе (выходе) последовательно-последовательно соединенных четы-
рехполюсников одинаковы. У-матрица параллельно-параллельно соединенных четырехполюсников равна сумме их У-матриц, так как ток на входе (выходе) эквивалентного четырехполюсника равен сумме токов на входе (выходе) параллельно-параллельно соединенных четырехполюсников, а напряжения на входе (выходе) у них одинаковы. Аналогично и в отношении /7-матрицы при последовательно-параллельном и С?-матрицы при параллельно-последовательном соединениях четырехполюсников. При каскадном соединении ток и напряжение на выходе первого четырехполюсника равны входным току и напряжению второго четырехполюсника, поэтому ^-матрица двух каскадно соединенных четырехполюсников а и b равна произведению Л-матриц этих четырехполюсников:
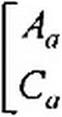 | 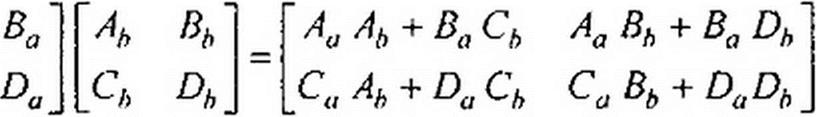 |
При параллельно-параллельном, последовательно-последовательном, параллельно-последовательном и последовательно-параллельном соединениях необходимо соблюдать условие регулярности соединения четырехполюсников — через оба первичных зажима каждого четырехполюсника должны течь равные по значению и противоположные по направлению токи; то же и по отношению к вторичным зажимам каждого четырехполюсника.








