§ 4.1 Определение четырехполюсника. Четырехполюсник — это обобщенное наименование электрической цепи, рассматриваемой по от­ношению к четырем ее зажимам.

Дата: 2025-06-02; Просмотры: 16
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Трансформатор, линию передачи энергии, мостовую схему и т. п. мож­но рассматривать как четырехполюсники.

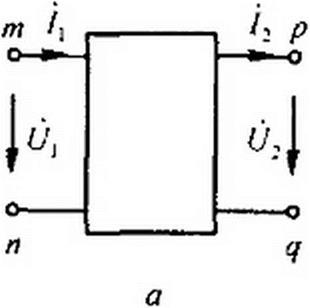
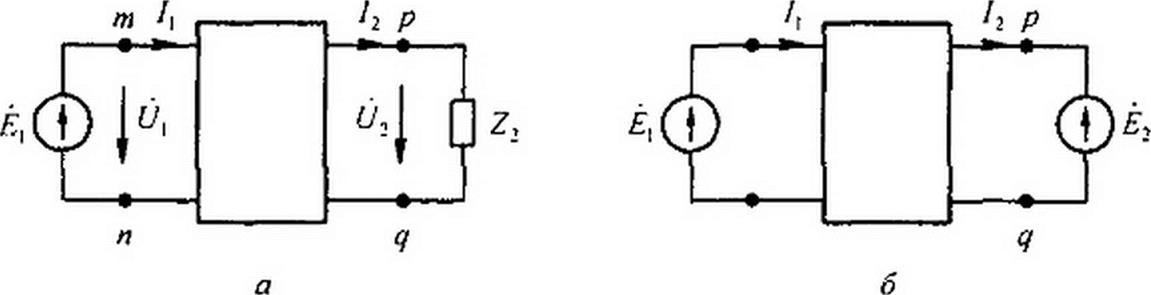
Принято изображать четырехполюсник в виде прямоугольника с выходящими из него концами (полюсами) тп и pq (рис. 4.1, а). Если че­тырехполюсник содержит источники электрической энергии, то в прямо­угольнике ставят букву А (активный); если буква А отсутствует, то эго значит, что четырехполюсник пассивный.

     
 


 
о Рис. 4.1
 


 
" q в

В общем, практически мало распространенном случае рабочими па­рами зажимов четырехполюсника могут быть три пары зажимов. При­менительно к рис. 4.1, а это, например, пары тп, рт и pq. В этом случае режим работы четырехполюсника определялся бы тремя независимыми уравнениями, в которые входили бы три независимых напряжения (что следует из второго закона Кирхгофа) между упомянутыми парами зажи­мов и тремя независимыми токами (что следует из первого закона Кирх­гофа). На практике четырехполюсник обычно работает в режиме, когда одна пара зажимов, например, тп, является входной, а другая пара, например pq — выходной. Четырехполюсник, у которого рабочими являются две пары зажимов, называют проходным. В данной главе рас­сматривается теория проходного четырехполюсника. (Термин «проход­ной» далее упоминаться не будет.)

Входной ток обозначают /ь входное напряжение— Ц; ток и напря­жение на выходе — /, и

Четырехполюсник является передаточным звеном между источником питания и нагрузкой. К входным зажимам тп, как правило, присоединя­ют источник питания, к выходным зажимам pq — нагрузку.

Предполагается, что нагрузка четырехполюсника и напряжение на входе при работе четырехполюсника в качестве связующего звена могут изменяться, но схема внутренних соединений четырехполюсника и со­противления в ней остаются неизменными.

§ 4.2 Шесть форм записи уравнений четырехполюсника. Четырех­полюсник характеризуется двумя напряжениями Ц и и двумя тока­ми jj и /2. Любые две величины из четырех можно определить через остальные. Так как число сочетаний из четырех по два равно шести, то возможны следующие шесть форм записи уравнений пассивного четы­рехполюсника:

/1-форма

= AU2 + Bi2; (4.1)

i}=CU2+D /2; (4.2)

У-форма

i} =Уци]+¥12й2, (4.3)

/2 =У21 47,+У22 ^2; (4.4)

Z-форма

i{ + z]2i2- (4.5)

02 = Z2I /, + Z22 /2; (4.6)

/7-форма

1X + H{1U2, (4.7)

/2=//2| /, + //22(>2; (4.8)

G-форма

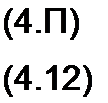/] - G)| + G]2 /2;

U2 “^21 ^^22 ^2 ’

В-форма

U2=B„l/] + Bl2 /2 — В2у t/j + В22

Обратим внимание на попарную инверсию У- и Z-форм, А- и 23-форм, Н- и G-форм.

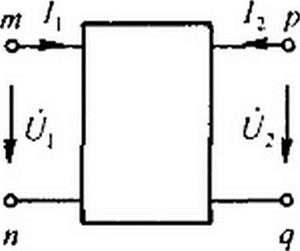
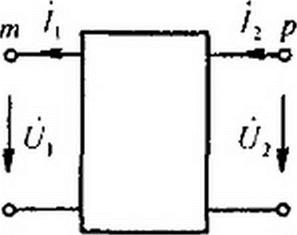
Исторически сложилось так, что для Л-формы (ее будем считать основной) положительные направления для токов и напряжений соответствуют рис. 4.1, а; для У-, Z-, Н-, G-форм — рис. 4.1,6, для В-формы — рис. 4.1, в.

Обратим внимание на то, что ток /2 на рис. 4.1, б направлен проти­воположно току /2 на рис. 4.1, а.

На рис. 4.1, в /, и /2 изменили направление по сравнению с токами /( и /2 на рис. 4.1, а.

Рассмотрение уравнений начнем с /1-формы.

§ 4.3 Вывод уравнений в /(-форме. Комплексные коэффициенты А, В, С, D в уравнениях (4.1) и (4.2) зависят от схемы внутренних соедине­ний четырехполюсника, значений сопротивлений схемы и частоты. Для каждого четырехполюсника их можно определить расчетным или опыт­ным путем. Для четырехполюсников, удовлетворяющих условию взаим­ности, коэффициенты связаны соотношением

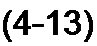A D-BC = \.

Выведем уравнения (4.1) и (4.2). С этой целью к зажимам тп подклю­чим источник ЭДС В = Umn ~ Ц, а к зажимам pq — нагрузку Z2 (рис. 4.2, а).

 


 
Рис 4.2

Напряжение на нагрузке U2 = /2 ^2 рц- Согласно теореме компен­сации (см. § 2.17), заменим нагрузку Z2 источником ЭДС с ЭДС Ё2 = й2 и направленной встречно току /7 (рис. 4.2, б). Запишем выражения для токов и Д, выразив их через ЭДС £ь £> и входные, и взаимные проводимости ветвей у,], у)2, у21, У22:

~ Ун ~ ^2 У12’ (4.14)

А = Ё] У2] ~ ^2 У 22- (4.15)

Если токи /t и /2 рассматривать как контурные, то ЭДС контуров, совпадающие с направлением контурных токов, войдут в уравнения, по­добные уравнению (2.7), со знаком плюс, а ЭДС, не совпадающие с на­правлением соответствующих контурных токов, — со знаком минус.

ЭДС Ё1 направлена согласно с поэтому она вошла в уравнения (4.14) и (4.15) со знаком плюс; ЭДС Е2 направлена встречно /2, поэто­му она вошла в эти уравнения со знаком минус.

Для линейных четырехполюсников, не содержащих нелинейных эле­ментов (для взаимных четырехполюсников), согласно принципу взаим-

ности (см. §2.16), у12 =^21- Из (4.15) найдем

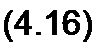
= Ё2^- + /2—.

У 21 У 2 J

Подставив (4.16) в (4.14), получим

j = Ё •Ин У2~ ~ У|2 'У'21 + i -^12.

У 21 2 ^21

Обозначим: