Двухполюсники на рис. 3.29, а, б, как и на рис. 3.29, в, г, называют эквивалентными, так как они имеют равные входные сопротивления при всех частотах.
§ 3.32 Передача энергии от активного двухполюсника нагрузке.
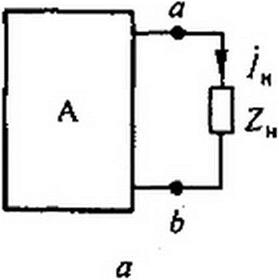
К зажимам ab активного двухполюсника (рис. 3.30, а) подключена нагрузка ZH = /?н ч- j Хн. Требуется выяснить, при соблюдении каких условий в нагрузке выделяется максимальная активная мощность.
По методу эквивалентного генератора (см. § 1.25) ток в нагрузке
/ — и ab х
'н
где ZH = Ян + j Хц — входное сопротивление двухполюсника по отношению к зажимам ab, поэтому
|
Oahx
*вх+*н+ЛЛх+*н)
По условию RBX и Хвх заданы и изменять их нельзя. Изменять можно лишь RH и Хн. Выберем такое Хн> чтобы ток в цепи был максимальным; это возможно, если Хвх + Хн =0. При этом двухполюсник работает в резонансном режиме — ток через нагрузку по фазе совпадает с напряжением Uahx- /н = Uabx '(*вх +^н)-
Как и в цепи постоянного тока (см. § 2.27), если взять Ян = Явх, выделяющаяся в нагрузке мощность максимальна:
Uabx
4 /?нч
ПА
Таким образом, чтобы выделить в нагрузке, присоединяемой к активному двухполюснику с входным сопротивлением RBX 4- J Хвх, максимально возможную мощность, необходимо выбрать следующие сопротивления нагрузки: Хв = -Хъх, RH = RBX.
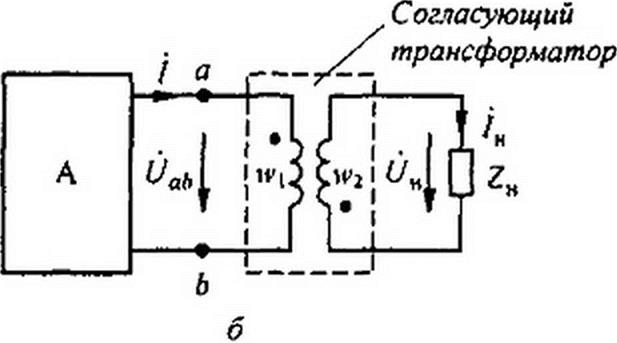
§ 3.33 Согласующий трансформатор. Нагрузкой двухполюсника может быть какое-либо уже существующее устройство, сопротивление которого ZH, так же как и входное сопротивление двухполюсника ZBX, задано и не может быть изменено. В этом случае согласование нагрузок с двухполюсником осуществляют, присоединяя нагрузку не непосредственно к зажимам двухполюсника, а через согласующий трансформатор (рис. 3.30, б). Обозначим через Wj и w2 число витков первичной и вторичной обмоток трансформатора. Активные сопротивления и индуктивности рассеяния обмоток весьма малы и при расчете не учитываем. Сердечник трансформатора (на рисунке не показан) выполнен из высококачественного магнитного материала с малыми потерями, поэтому ток холостого хода трансформатора мал по сравнению с током по обмотке W] при нагрузке. Такой трансформатор по своим свойствам приближается к трансформатору, который называют идеальным (см. § 3.34). Для него справедливы соотношения (обозначения соответствуют рис. 3.30, б) / Wj -7Н w2 я= 0, (jQh/Un - Wj /w2. Пояснения к этим формулам см. в § 15.67 (обозначения согласуются так: Uof) =U{, и / = ). Входное сопротивление изображенной штриховой линией части схемы по отношению к зажимам ab
 |
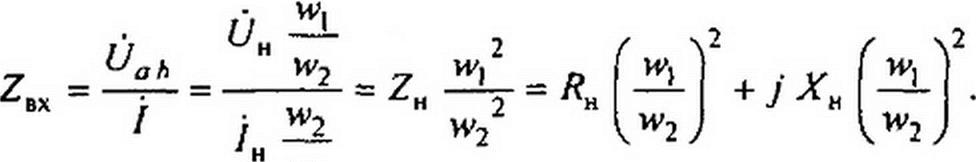В соответствии с § 3.32 это сопротивление должно быть комплексносопряженным с сопротивлением двухполюсника: ZBX = + j Хвх.
Отсюда следует, что для согласования по активному сопротивлению Явх = (wj/w,)2, а Для согласования по реактивному сопротивлению
(wj / w2)2. Отношение чисел витков и», /м>2 определим из первого условия w} / и-s = ^Лвх / RH. При выборе числа витков wt и площади поперечного сечения сердечника трансформатора 5 должно быть учтено, что в установившемся режиме работы амплитудное значение потока в сердечнике не должно достигать потока насыщения этого сердечника, иначе будет нарушено условие /, - /н w2 » 0. Для выполнения со
гласования по реактивному сопротивлению последовательно с нагрузкой включают дополнительное сопротивление соответствующего характера.
§ 3.34 Идеальный трансформатор. В качестве элементов схем замещения электрических цепей наряду с R, L, С, М в литературе используют идеальный трансформатор (ИТ).
Идеальным называют трансформатор без потерь, у которого входные и выходные токи и напряжения связаны соотношениями Ц = К U2, 12 - К 1[у где К = w, / и>2 — коэффициент трансформации. Идеальный трансформатор трансформирует напряжение в напряжении ток /j — в ток /2, сопротивление нагрузки Z — в сопротивление /С2 Z (см. § 3.33).
§ 3.35 Падение и потеря напряжения в линии передачи энергии. Генератор соединен с приемником энергии линией передачи, которая обладает активным /?л и индуктивным X п = to Ln сопротивлениями.
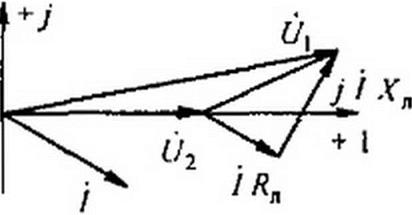
Построим векторную диаграмму для цепи, состоящей из генератора, линии передачи и приемника. Для определенности положим, что нагрузка приемника имеет индуктивный характер. Вектор напряжения в конце линии (на приемнике) направим по оси + 1 (рис. 3.31); вектор тока / отстает от него в силу индук
|
тивного характера нагрузки. Падение напряжения в активном сопротивлении линии / R„ совпадает по фазе с током, падение напряжения в индуктивном сопротивлении / j Хп опережает ток на 90°
Под падением напряжения в линии передачи понимают модуль геометрической разности векторов в начале ({?,) и конце (t/2) линии:
/Д2+(<о £л)2.
Потеря напряжения в линии передачи равна разности модулей напряжения в начале и конце линии, т е. (t/, | -1 (72 |. Потеря напряжения показывает, на сколько вольт напряжение в конце линии меньше, чем напряжение в ее начале.
Как правило, падение напряжения больше потери напряжения.
§ 3.36 Расчет электрических цепей при наличии в них магнитносвязанных катушек. В состав электрических цепей могут входить катушки, магнитно-связанные с другими катушками. Поток одной из них пронизывает другие и наводит в них ЭДС взаимоиндукции, которые должны быть учтены при расчете. При составлении уравнений для магнитно-связанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции.
Правильное заключение об этом можно сделать, если известно направление намотки катушек на сердечнике и выбрано положительное направление токов в них.
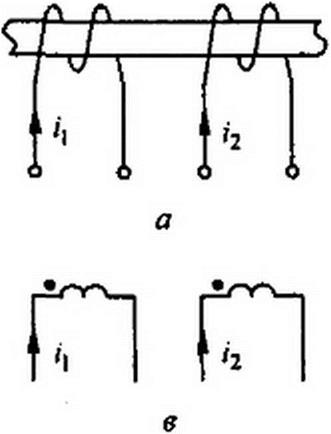
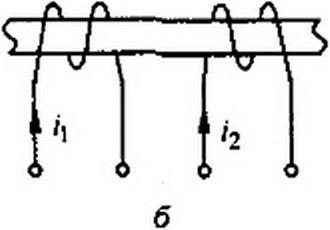
На рис. 3.32, а катушки включены согласно, на рис. 3.32, 6 — встречно. Чтобы не загромождать чертеж, сердечники катушек на электрических схемах обычно не изображают, ограничиваясь тем, что одноименные
 | |||||
 | |||||
 | |||||
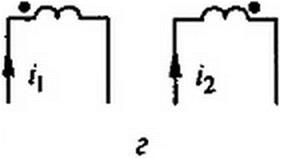Рис. 3.32
зажимы (например, начала катушек) помечают одинаковыми значками, например точками.
Схема на рис. 3.32, в эквивалентна схеме на рис. 3.32, а, а схема на рис. 3.32, г — схеме на рис. 3.32, б.
|
Если на электрической схеме токи двух магнитно-связанных катушек относительно одноименно обозначенных зажимов, например оба направлены к точкам или оба направлены от точек, то имеет место согласное включение, в противном случае — встречное.
Если магнитно связано несколько катушек, то начало и конец размечают для каждой пары катушек отдельно.
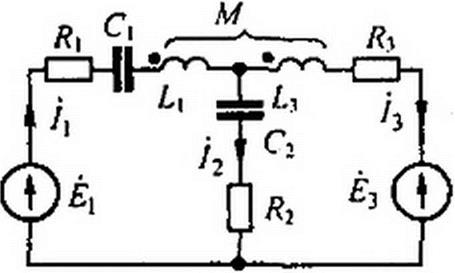
На примере рис. 3.33 рассмотрим методику составления уравнений для расчета магнитно-связанных цепей. Произвольно выберем положительные направления токов
в ветвях схемы. Направления обхода контуров выберем по часовой стрелке. Составим уравнения для мгновенных значений: = /2 + /3.
Для левого контура (первая и вторая ветви)
I, Я.+2-р, </< + £, ^+Л/^ + ^-р2Л + «2Я2=е,. (3.63)
п f di\
Перед слагаемым М поставлен тот же знак, что и перед Д
так как токи и /3 входят в одноименные зажимы магнитно-связанных катушек, т. е. имеет место согласное включение. Сумма слагаемых
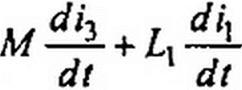представляет собой падение напряжения на первой
катушке.
Слагаемые левой части уравнения (3.63) взяты со знаком плюс, так как на всех участках первого контура положительные направления токов совпадают с направлением обхода контура.
Составим уравнение для правого контура (вторая и третья ветви). Направление тока i2 встречно направлению обхода контура, поэтому сумма падений напряжений во второй ветви войдет в уравнение со знаком минус:
1 е. , , _ , d i-> , d.
~7“ J'2 ■ ь Л2 + £3 ”77 + м — + /3 /?3 = -е3.
u? dt
 |
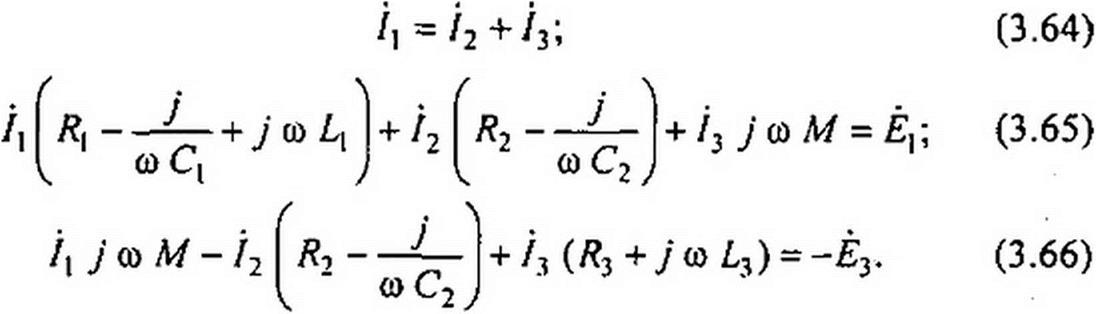В комплексной форме записи:
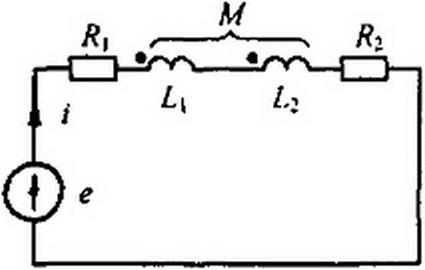
§ 3.37 Последовательное соединение двух магнитно-связанных катушек. На рис. 3.34 изображена схема последовательного согласного включения двух катушек, а на рис. 3.35 — последовательного встречного включения тех же катушек.
 |
|
 |
|
При согласном включении
В комплексной форме записи:
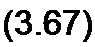/(Я1+Я2+уш(£|+£2+2Л/))*Ё; /ZcorjI =£;
^согл = £| + + У й (^1 + ^2 + 2 ^)'
 |
|
 |
|
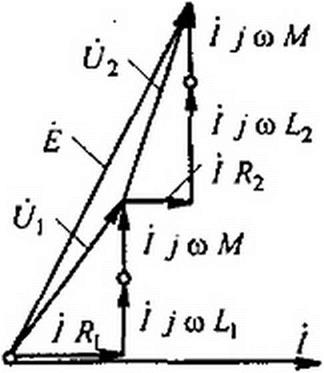
Векторная диаграмма для согласного включения изображена на рис. 3.36, где U}— напряжение на первой катушке; U2— на второй.
При встречном включении
|
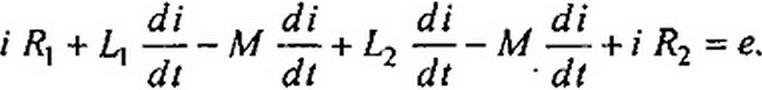
Отсюда
где
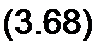Астр = /?1 +л2 w(L| +£2 -2 М).
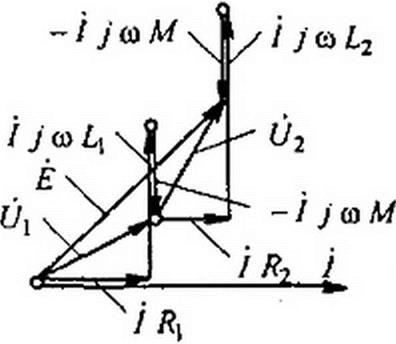
Векторная диаграмма для встречного включения при L} > М и > М изображена на рис. 3.37.
§ 3.38 Определение взаимной индуктивности опытным путем.
Обсудим два практически важных способа опытного определения взаимной индуктивности М двух магнитно-связанных катушек.
Первый способ. Проделаем два опыта. В первом включим катушки последовательно и согласно. Измерим ток и напряжение на входе и активную мощность цепи. Во втором те же катушки включим последовательно и встречно и также измерим /, U, Р. По результатам измерений найдем:
^согл - w (^i + А + 2 W);
ЛВС1р=со(£) + Д3-2Л/).
Разность А"согл - %BCTP = 4 со М, следовательно,
Y — X
согл встр
4 со
Второй способ. Подключим первую катушку к источнику синусоидальной ЭДС через амперметр (рис. 3.38), а к зажимам второй катушки присоединим вольтметр с большим внутренним сопротивлением. Измерим ток /| и напряжение С/2.
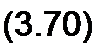Мгновенное значение напряжения и2 = М Его действующее значение (72=соЛ/ Следовательно,
(O/j '
Пример 45. В схеме (см. рис. 3.38) вольтметр показал ТОО В, амперметр 10 А; е> = 314 рад/с. Определить М.
Решение. По формуле (3.70), Л/ = 100/(314-10) = 0,0319 Гн.
§ 3.39 Трансформатор. Вносимое сопротивление. Трансформатор представляет собой статическое (т. е. не имеющее подвижных частей) устройство, служащее для преобразования числового значения переменного во времени напряжения, а также для электрического разделения цепей и преобразования числовых значений сопротивлений. Передача энергии из одной цепи в другую производится трансформатором благодаря явлению взаимоиндукции.
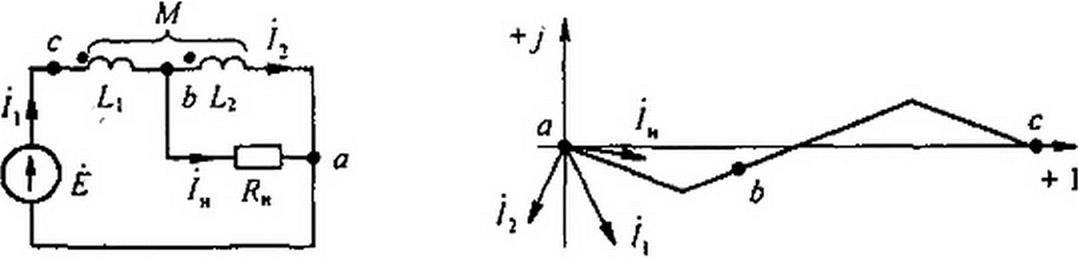
Трансформатор имеет две обмотки, находящиеся на общем сердечнике. Магнитную проницаемость сердечника будем полагать постоянной. Параметры первичной обмотки— и вторичной— R2 и Вза- имная индуктивность между обмотками — М(рис. 3.39, а). Сопротивление нагрузки, подключенной к зажимам вторичной обмотки, равно ZH.
 |
|
 |
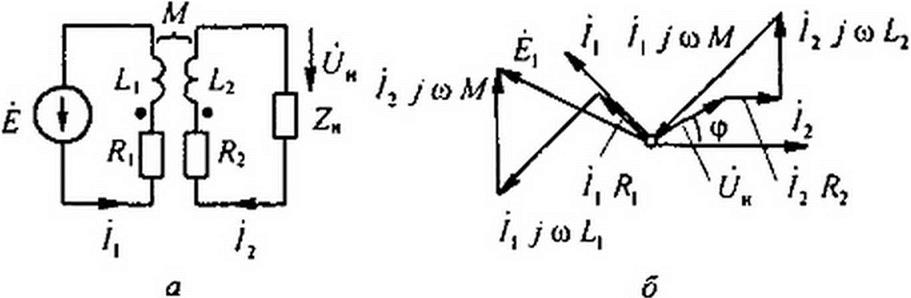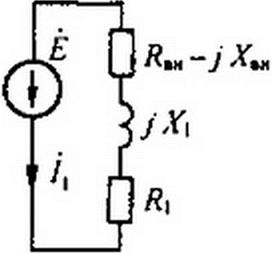Выберем положительные направления токов /, и /2. Обозначим напряжение на нагрузке 0н. Запишем уравнения в комплексной форме — для первичной цепи:
♦ • • •
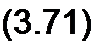h Л| + /| j А, + /2 J со М = E;
для вторичной цепи:
/2 /?2 + /2;соЕ2 + /1(/фЛ/ + (/н=О. (3.72)
На рис. 3.39, б качественно построим векторную диаграмму, полагая, что нагрузка ZH = zH е7 Фи имеет индуктивный характер. Ток /2 направим по оси + I. Напряжение на нагрузке (У опережает ток /2 на Угол <рн. Падение напряжения /2 R2 совпадает по фазе с током /2. Вектор /2уо>£2 опережает вектор тока /, на 90°.
В соответствии с уравнением (3.72) вектор А проводим так, чтобы геометрическая сумма падений напряжений во вторичной цепи равнялась нулю.
Вектор тока Ц отстает от вектора A J с& М на 90°. Вектор A R\ совпадает с вектором тока А по фазе, а вектор /t j со опережает вектор А на 90°.
Вектор I2 jсо М опережает вектор /2 на 90°. В соответствии с уравнением (3.71) геометрическая сумма A R\ + A j <о Д + /2 J со Л/ дает
Подставим в (3.72) (7Н = /2 ZH = /2 (Ян + j X*) и решим уравнения (3.71) и (3.72) относительно А •
А
(Л1+Л.н) + Л''1-*,«)’
где /?вн и А\н— вносимые из вторичного контура в первичный активное и реактивное сопротивления. При этом
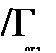
________ со2 М2________
(Я2 + Ян)2+(<о £2+Лн)2
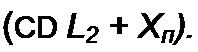со2 М2
(л2 + /?и)2+(ф л2+а;)2
Вносимые сопротивления представляют собой такие сопротивления, которые следовало бы «внести» в первичную цепь (включить последовательно с и Х}), чтобы учесть влияние нагрузки вторичной цепи трансформатора на ток в его первичной цепи (рис. 3.39, в).
 |
| ||||
| ||||
Решение. Составим уравнения по законам Кирхгофа. По первому закону Кирхгофа, /| = 12 +
При составлении уравнений по второму закону Кирхгофа обход контуров будем совершать по часовой стрелке. Тогда
/| j to L\ + /2 j to M + /н Rn ~ Е\
/| j to М + /2 j to L2- I* Rn = 0.
В двух последних уравнениях заменим /н А (/?н + у©£,)+/2 (у© Л/-/?н)= £2;
Подставим числовые значения:
А (4 + 2у) + 72 (у-4) = 100;
Решение уравнений дает:
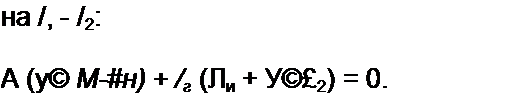
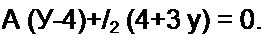А = 17,7е’'63° А; /2 = 14,6 e-j/И4° А; /н = А-/2 = 14,12 е^9’54'А.
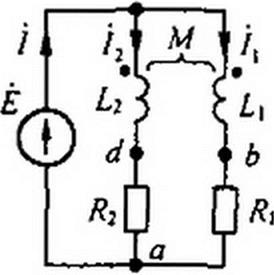
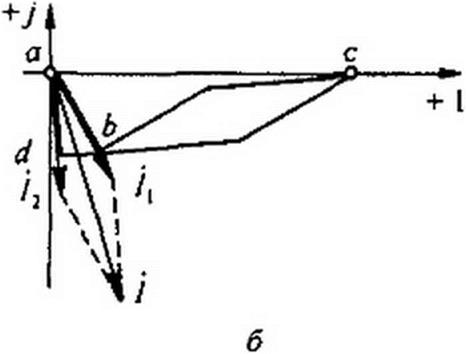
На рис. 3.40. б изображены топографическая диаграмма и совмещенная с ней векторная диаграмма токов.
 |
|
|
 |
|
Пример 47. Построить топографическую диаграмму для схемы (рис. 3.41, а), совместив ее с векторной диаграммой токов. Две ветви схемы связаны магнитно. Значения параметров: © Z.J = 3 Ом; ©£2 = 4 0м; со Л/= 3 Ом; /?|=Л2 = 2 0м; £ = 100 В.
Решение. Обозначим токи в ветвях через и /2 и ток в неразветвленной части схемы — через 1. Составим уравнения по второму закону Кирхгофа для согласного включения катушек:
А (Л] + У © £|)+ /2 у © А/ = £; /, j о М + /2 (Л2 + J а> L2) = £.
Совместное их решение дает. А = 16е"у6<г А; /2 = 16е"?86‘3<х А.
Топографическая диаграмма, совмещенная с векторной диаграммой токов, изображена на рис. 3.41, б.
Рассмотрим вопрос о переносе мощности из одной ветви в другую вследствие магнитной связи. Если ветвь к с током 1к и ветвь q с током А связаны магнитно и взаимная индуктивность между ветвями Л/, то магнитный поток из ветви к в ветвь q переносит комплексную мощность, равную произведению ЭДС взаимоиндукции в еу-ветви Ту о Л/ 1к, на сопряженный комплекс тока (/-ветви, т. е. / ;
S=(?j(oЛ//*)/*.
Знак минус соответствует согласному, плюс — встречному соединению.
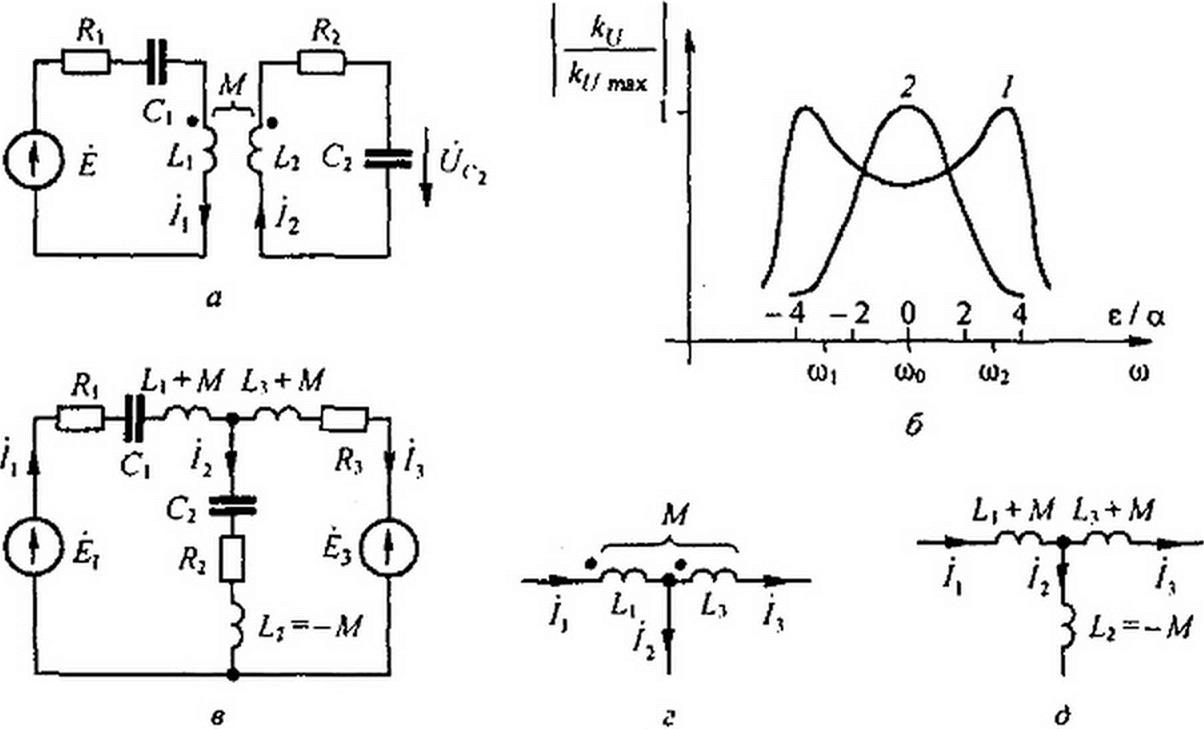
§3.40. Резонанс в магнитно-связанных колебательных контурах. В §3.23-3.27 были описаны резонансные явления в параллельном, последовательном и последовательнопараллельном резонансных контурах. Рассмотрим резонанс в магнитно-связанных
контурах, например в схеме (рис. 3.42, а), часто применяемой в радиотехнике. Для упрощения выкладок положим £( = £2 = L, Q = С2 =С; Л[ = R2 - R, что дает возможность относительно легко выявить основные закономерности резонанса в этой схеме.
 |
|
Составим уравнения по второму закону Кирхгофа:
/j j + у со £ ——• I - /2 j to М ~ Ё\
<0 С j
- 7> j о М + /, I R + j to £ —— ] = 0.
1 Ч шС J
j to M E
R + j w £ —— + to2 M 2
toCj
Напряжение на конденсаторе второго контура
 |
« •
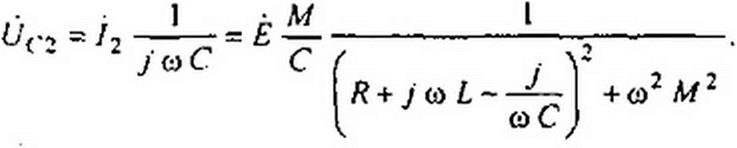Пусть t/(-2 / Е = к(/. тогда
 | |||
 | |||
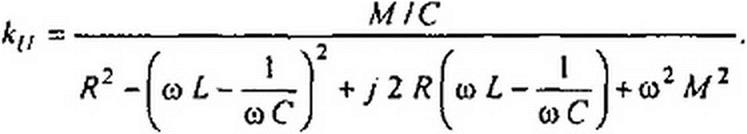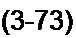Обозначим
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
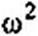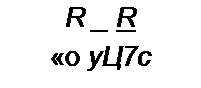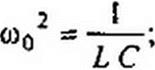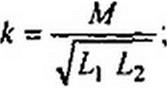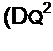С помощью параметра £ учитывается отклонение текущей частоты <и от резонанс* ной о0. Рассмотрим работу схемы при относительно малых отклонениях to от о>о. Положим to = <оо - Део. Тогда
to2 соо2 - со2 (е>0-со)(<о0+со) 2 Део - ~ - - - -
2 2 2
<00 (,)0 <оо
В свою очередь.
При малых отклонениях <о от ю0, вынеся в знаменателе выражения (3.73) за скобку а2I? = ы02 L2 и использовав указанные обозначения, получим
Модуль
 |
|
 |
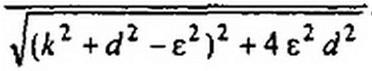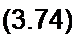При фиксированных к и d можно исследовать | ки | на экстремум в функции £ для двух случаев: k>d и k<d.
При k>d имеются три экстремума: минимум при е = 0, т. е. при <о = <о0, и два мак* симума при с, 2 - ~ d2, которым соответствуют частоты to, , = соо ^1-е, 2 •
Резонансная кривая при этом имеет два горба (кривая 1 на рис. 3.42, б построена при к = 3d). С увеличением к горбы кривой раздвигаются.
При k<d имеется только один экстремум: максимум при е = 0 (кривая 2 на рис. 3.42. б). По оси абсцисс на этом рисунке отложено г /d, по оси ординат «е 1*(,т„|=1/(2</) = -ЛТс/2Я.
Ток первичного контура в функции от г /d при к > 0,49 d имеет двугорбую форму.
3.41 3.41. «Развязывание» магнитно-связанных целей. Иногда в литературе можно встретить расчетный метод, который называют развязыванием магнитно-связанных цепей (катушек). Метод состоит в том, что исходную схему с магнитно-связанными индуктивностями путем введения дополнительных индуктивностей и изменения величины имевшихся преобразуют так, что магнитная связь между всеми индуктивностями в преобразованной схеме будет отсутствовать.
Так как преобразования осуществляют на основе составленных по законам Кирхгофа уравнений для исходной схемы, то вновь полученная и исходная схемы в расчетном смысле полностью эквивалентны, а расчет схемы после развязывания упрощается за счет возможности применения метода узловых потенциалов.
Составим, например, схему, эквивалентную схеме на рис. 3.33. С этой целью в уравнении (3.65) заменим /3 на /t - /2 ив уравнении (3.66) —
на /, +1у. Замену одних токов другими производим так, чтобы в каж
дое из получающихся после замены уравнений входили только те токи, которые текут в ветвях рассматриваемого контура.
В результате получим:
 |
|
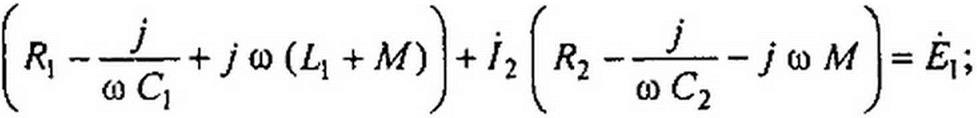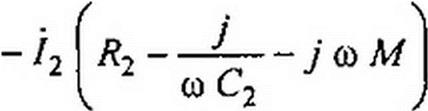
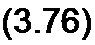
ь •
+ /3 (/?2 <о £| + j w М)- -Е3.
Уравнениям (3.75) и (3.76) соответствует схема на рис. 3.42, в. Сопоставляя схемы на рис. 3.33 и рис. 3.42, в, замечаем, что £j заменена на (£] + Л/), £3— на (£3 + М), а во вторую ветвь введена отрицательная индуктивность L2 = -М (физически осуществить полученную расчетным путем отрицательную индуктивность в цепи только с линейными элементами невозможно). Таким образом, участок цепи, изображенный на рис. 3.42, г, в расчетном смысле может быть заменен участком, показанным на рис. 3.42, д. Если катушки будут включены встречно, то на рис. 3.42, д следует изменить знак перед М. Покажем, как можно осуществлять развязывание, не составляя полных уравнений по второму закону Кирхгофа. В основу положим неизменность потокосцепления каждого контура до и после развязывания. Пусть в схеме (рис. 3.33) после развязывания х — индуктивность первой ветви, у — второй, z — третьей. Условие неизменности потокосцепления левого контура:
ц L} + i3 М = i} + 0| -i2) M = i} x + /2 у,
откуда х = £, + М и у = -М.
Условие неизменности потокосцепления правого контура
'i М + /3 £3 = (/2 + /3) М + /3 £3 = i3 z - /2 у,
откуда у = -М и z = М + L3. Знак минус поставлен потому, что при обходе контура по часовой стрелке перемещаемся встречно току /2.
3.42 . Теорема о балансе активных и реактивных мощностей (теорема Лонже- вена). В любой линейной электрической цепи сумма активных мощностей источников ЭДС равна сумме активных мощностей приемников, а сумма реактивных мощностей источников ЭДС — сумме реактивных мощностей приемников энергии.
Пусть схема содержит / узлов, b ветвей и все ветви или часть их связаны друг с другом магнитно. По первому закону Кирхгофа сумма токов в любом узле равна нулю. Например, для A-узла, в котором сходится п ветвей, £/^=о или £4 = о.
Умножим каждое слагаемое этой суммы на потенциал £-узла
« ♦
ф* =0-
/>=1
Просуммируем аналогичные выражения для всех /-узлов схемы:
А=1 л=1
В двойную сумму любой ток схемы, например ток 1тч, входит дважды и притом с разными знаками. Действительно, при к-т и P-q слагаемое равно фда i а при k = q и р-т равно ©/' Так как 1 = то эти слагаемые можно объединить и получить /m<? (<pm - ). Положим, что какая-то ветвь схемы, например ветвь kq магнитно связана с вет
|
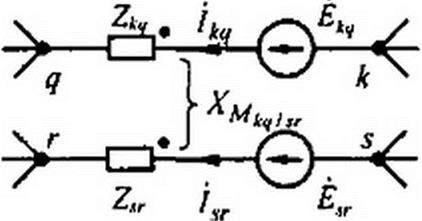
вью sr так, что сопротивление взаимоиндукции между ними XMk Itr (рис. 3.43).
В соответствии С рис. 3.43
для ветви qk
Ф<? " Фа = &kq - hq Zkq - f sr J XMkqhr i
для ветви sr
фг -фЛ. = £^- - liT Zy ~ /ty J
Если принять !k(f = Iktf eJ ; ixf = е7Ф'\ и учесть /^ =/А</е’7Ф*’ и
К = Avr е"7 Флг, то сумма двух слагаемых itr j Хм + lk4 hr j Хм h4 1„ = = Л, /». Мм,„„ (e-'(’‘,'’,’'> + e'/‘’'’''’'>) = J2X4v4r7i, I, со5(ф,,-ф„).
Таким образом, попарное рассмотрение слагаемых двойной суммы позволяет переписать ее в виде:
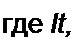й k q ?кд ~ Е ^Atf + J Е I sr ^Mkq!xr c^(^kq ~Флг)> (3.77)
кч — квадрат модуля тока ветви kq\ Zk<J = Rkq + j Xkq-
Левая и правая части формулы {3.77) представляют собой комплексы. Равенство действительных частей комплексов
'»«*>«• <3 78> равенство мнимых частей
Im I kq = Z + 2 E l kq I.<r XMk„lsr <*>^kq ~ Ф,г )• (3 79>
В этом выражении принято положительным при согласном направлении по
токов взаимоиндукции и самоиндукции ветвей kq и sr и отрицательным при встречном их направлении. Формулы (3.78) и (3.79) являются математической записью сформулированной теоремы.
Пример 48. По данным примера 46 убедиться в справедливости теоремы о балансе мощности применительно к схеме на рис. 3.40, а.
Решение. Активная мощность, доставляемая источником ЭДС,
Re £ / = Re 100 • 17.7 с'6Г = 1770 cos 63° = 800 Вт.
Активная мощность, потребляемая приемниками, /?н = I4.I22 - 4 = 800 Вт. Следовательно. равенство активных мощностей действительно выполнено. Реактивная мощность источника ЭДС 1m £ / = 1770 sin 63° = 1582 ВАР. Реактивная мощность приемников энергии с учетом согласного включения катушек
/2 <о £[ + /22 о L2 + 2 /| /2 to М cos(<p,| - ф,2) =
17,72 • 2 +14.62 • 3 + 2 ■ 17,7 ■ 14,6 cos(63° -144°) = 1582 ВАР.
Таким образом, баланс реактивных мощностей тоже удовлетворяется.
§ 3.43 Теорема Теллегена. Пусть в некоторой схеме имеется п ветвей и узловая матрица ее (Л). Матрицу-столбец комплексно-сопряженных токов ветвей обозначим [/д], а матрицу-столбец комплексных напряжений на ветвях (включая ЭДС ветвей и падение напряжения на них) обозначим [()н J.
В соответствии с законом сохранения энергии
 | |||
 | |||
|
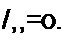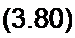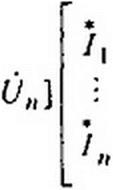
Соотношение (3.80) можно записать так:
(3.81)
Но в соответствии с § 2.35 [(?л] = (/}z [<р], где [ф!— матрица-столбец потенциалов незазсмленных узлов.
В свою очередь,
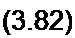
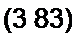(««I' =(<pf И
Подставим (3.82) в (3.81):
[ф|’М)(/Д = 0.
рмуле (3.83) произведение [Л][/д]= 0 физически выражает собой систему урав
нений по первому закону Кирхгофа для незаземленных узлов схемы, составленную для комплексно-сопряженных токов ветвей.
Из (3.83) следует, что если в одной и той же схеме с неизменной (Л)-матрицей создать два режима, отличающихся сопротивлениями и ЭДС ветвей, и всем величинам, относящимся к первому режиму, присвоить один штрих, а ко второму — два, то
(3.84)
Соотношение (3.84), получившее название теоремы Теллегена. справедливо и по отношению к режимам в двух разных схемах, лишь бы у них были одинаковые узловые [Л]-матрицы.
§ 3.44 Определение дуальной цепи. Две электрические цепи называют дуальными, если закон изменения контурных токов в одной из них подобен закону изменения узловых потенциалов в другой. В качестве простейшего примера на рис. 3.44 изображены две дуальные цепи.
 |
а б
Рис. 3.44
Схема на рис. 3.44, а состоит из источника ЭДС Е и последовательно с ним включенных активного, индуктивного и емкостного элементов (/?, £, С). Схема на рис. 3.44, б состоит из источника тока ,7Э и трех параллельных ветвей. Первая ветвь содержит активную проводимость вторая — емкость Сэ, третья — индуктивность
Для того чтобы показать, какого рода соответствие имеет место в дуальных цепях, составим для схемы на рис. 3.44, а уравнение по методу контурных токов:
j о>С
а для схемы на рис. 3.44, б — по методу узловых потенциалов, обозначив потенциал точки а через фа, положив равным нулю потенциал второго узла:
(3.86)
Если параметры £э. Сэ, схемы (рис. 3.44, б) согласовать с па
раметрами /?, L, С схемы (рис. 3.44, а) таким образом, что
 |  | ||
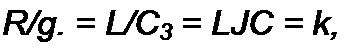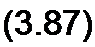где к — некоторое произвольное число (масштабный множитель преобразования), Ом2, то
 |
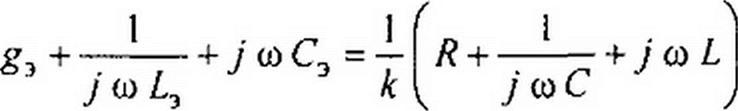С учетом равенства (3.88) перепишем уравнение (3.86) следующим образом:
(3.89)
Из сопоставления уравнений (3.85) и (3.89) следует, что если ток источника тока в схеме на рис. 3.44, б изменяется с той же угловой частотой, что и ЭДС Ё в схеме на рис. 3.44, а, и численно равен Ё, а параметры обеих схем согласованы в соответствии с уравнением (3.87), то при к = 1 Ом2, закон изменения во времени потенциала фа в схеме на рис. 3.44, б совпадет с законом изменения во времени тока / в схеме на рис. 3.44, а.
Если свойства какой-либо из схем изучены, то они полностью могут быть перенесены на дуальную ей схему.
Между входным сопротивлением ZBCX исходного двухполюсника и входной проводимостью Кдуал дуального ему двухполюсника существует соотношение ZBCX -к Удуал.
Из (3.88) получаем соотношение между частотной характеристикой чисто реактивного исходного двухполюсника Хисх((о) и частотной характеристикой дуального ему тоже чисто реактивного двухполюсника
^дуал(ш)' Действительно, так как ZHCX = j >VMCX(co), а ^дуал = - J £дуал (<о), то Л'исх = -к ЬяуалМ, т. е. частотная характеристика дуального двухполюсника получается из исходной частотной характеристики путем опрокидывания ее относительно оси и деления на масштабный множитель к.