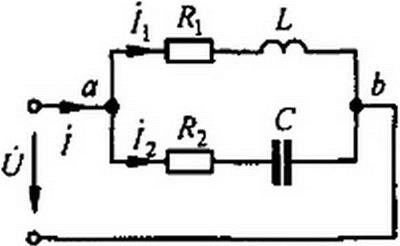
§ 3.26. Резонанс токов. Явление резонанса в схеме (рис. 3.25, а), об­разованной двумя параллельными ветвями с разнохарактерными реактив­ными сопротивлениями, называют резонансом токов.

Дата: 2025-06-02; Просмотры: 15

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Пусть первая ветвь содержит активное сопротивление R_} и индуктив­ное со £, а вторая ветвь — активное R₂ ^и емкостное 1/соС.

Ток в первой ветви отстает от напряжения 0 ~lJ_ah (рис. 3.25, б) и может быть записан как

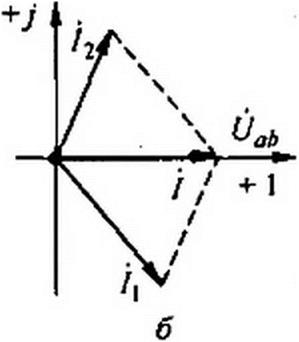Рис. 3,25

/,=(7>1=^(g₁-j6_l).

Ток /₂ во второй ветви опережает напряжение:

/₂=У/₂=У(52-7Л).

Ток в неразветвленной части цепи

/ = А +/₂ +g₂)-7^(^i +^)«

По определению резонансного режима ток / должен совпадать по фазе с напряжением U. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю: Ь_} + Ь₂ - 0.

В соответствии с (3.38)

Следовательно, условие наступления режима резонанса токов в схе­ме на рис. 3.25, а можно записать так:

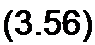to L __ I / со С

+ со² L² " R] + 1/со²С² *

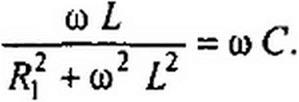На рис. 3.25, б изображена векторная диаграмма для резонансного режима. Из (3.56) следует, что если R₂ = 0, то резонанс наступит при

(3.57)

В еще более частном случае, когда R₂ =0 и R\ «coL, резонанс на­ступит при

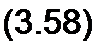со² £С~1.

Резонанса можно достичь изменением со, £, С или R_} и R₂. Число­вое значение тока в неразветвленной части схемы может быть меньше токов в ветвях схемы. При R₂ = 0, » 0 ток / может оказаться ничтож­

но малым по сравнению с токами /, и /₂.

В идеализированном, практически не выполнимом режиме работы, когда Я, = Я₂ =0, ток в неразветвленной части схемы на рис. 3.25, а равен нулю и входное сопротивление равно бесконечности.

Обратим внимание на следующее. В формулу (3.56) входит пять величин (L, С, Я_и Я₂, ©)• Если определять из нее L или С, то может оказаться, что для искомой величины будут получены одно или два дей­ствительных значения либо мнимое значение.

Получение двух действительных значений для L и С свидетельствует о том, что при неизменных четырех параметрах вследствие изменения пятого можно получить два резонансных режима. (Пояснения к возник­новению двух резонансных режимов при изменении одного параметра и неизменных остальных даются в примере 54.)

Получение мнимых значений L и С свидетельствует о том, что при данных сочетаниях параметров резонанс невозможен.

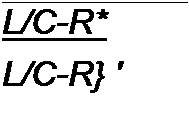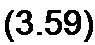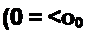Определим w из (3.56):

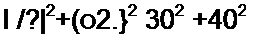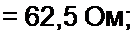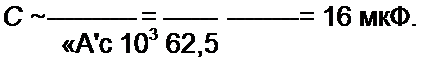где со₀ = 1/yl~L~C— резонансная частота в контуре без потерь при /?1 = /?₂ — 0.

Поскольку угловая частота действительна и положительна, то числи­тель и знаменатель формулы (3.59) должны быть с одинаковыми знака­ми. Это имеет место при

а) I/O/?!²; £/С>Я₂²;

б) LIC<tf-, L/C<R₂.

При R_x = R₂ частота (о - w₀. При L/C - Я² = Я²

со = со_о Vo/0,

т. е. со получается величиной неопределенной. Физически это означает, что резонанс может возникать при любой частоте. Сопротивление парал­лельного контура равно J— = Я, = Я₂.

V

Пример 43. В схеме (рис. 3.25, а) /?₍=ЗООм; а £ = 40 Ом; Я₂=0; cj = 10^Jpaa/c. При каком значении емкости конденсатора в схеме будет резонанс токов?

Ре ш е н и е. По формуле (3.56)

§ 3.27 Компенсация сдвига фаз. Входное сопротивление большин­ства потребителей электрической энергии имеет индуктивный характер. Для того чтобы уменьшить потребляемый ими ток за счет снижения его
реактивной составляющей и тем снизить потери энергии в генераторе и подводящих проводах, параллельно приемнику энергии включают бата­рею конденсаторов.

Уменьшение сдвига фаз между напряжением на приемнике и током, потребляемым от генератора, называют компенсацией сдвига фаз.

Компенсация сдвига фаз существенна для энергоемких потребителей, например крупных заводов. Осуществляется она в месте ввода линии питания в распределительном устройстве. Экономически выгодно подключать конденсаторы на возможно более высокое напряжение (ток через конденсаторы 1_C~U со С). Сдвиг фаз ср между напряжением и током, потребляемым от источника питания, доводят до значения, при котором cos ср « 0,9-г 0,95.