Совокупность точек комплексной плоскости, изображающих комплек­сные потенциалы одноименных точек электрической схемы, называют топографической диаграммой.

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Термин «топографическая» объясняется тем, что диаграмма напоми­нает топографическую карту местности, где каждой точке местности отвечает определенная точка карты. Расстояние между двумя точками на местности можно определить, измерив расстояние между одноименны­

ми точками на карте.

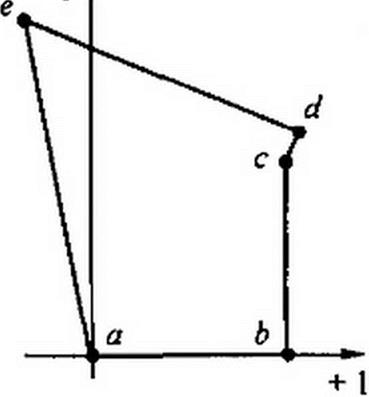
Аналогичные измерения можно проводить и на топографической диа­грамме. Напряжение между любыми двумя точками электрической схе­мы, например между точками а и Ь, по значению и направлению опре­деляется вектором, проведенным на топографической диаграмме отточ­ки Ъ к точке а.

При построении топографической диаграммы, как и потенциальной (см. § 2.10), потенциал любой точки схемы может быть принят равным нулю. На диаграмме эту точку помещают в начало координат. Тогда по­ложение остальных точек схемы на диаграмме определяется параметра­ми цепи, ЭДС и токами ветвей. Рассмотрим несколько примеров.

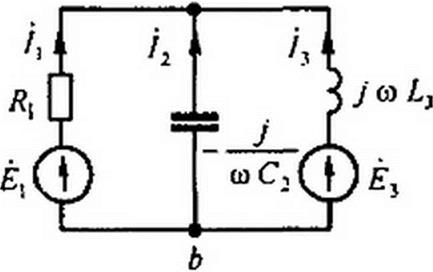
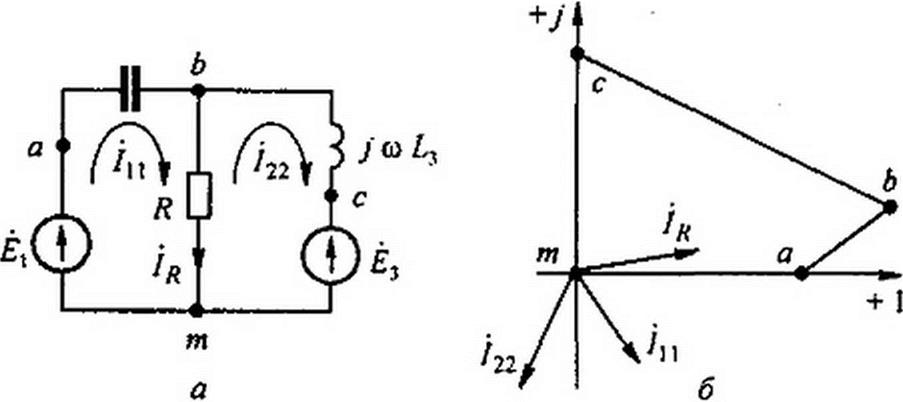
Пример 37. По данным примера 35 построить топографическую диаграмму для схе­мы рис. 3.16, а.

Решение. Обозначим буквами а, Ь. с,... точки схемы на рис. 3.16. а. которые хо­тим отобразить на топографической диаграмме. Примем потенциал тонкий равным нулю: = 0.

Выразим потенциал точки b через потенциал точки а:

Фь = Ф_в + А Kj = Ф_О + ю.

Знак плюс перед слагаемым j_} Я, обусловлен тем, что при переходе от точки а к точ­ке b перемещение происходит навстречу току /₍ (при тгом потенциал увеличивается на /?|). Точка b на диаграмме имеет координату по оси абсцисс + 10. Аналогично

Фо = Фл + Л =10 + 7 Ю;

Ф</ = Фо + 6 /?з’.

Фе =Ф</ +Л у w Aj.

Совокупность точек a. b. с, d. е на комплексной плоскости (рис. 3.18) представляет собой топографическую диаграмму схемы на рис. 3.16. а. По ней удобно определять на-

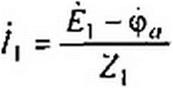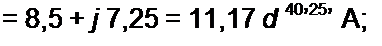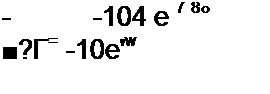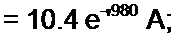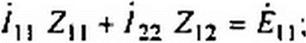где Z_l}— собственное сопротивление первого контура; Z_u = R--^— = 5-2 j\ Z_r — (!)C

собственное сопротивление второго контура, Z₂₂ = R + j w L = 5 + 5 j, Z_]2 = Z₂| — сопро­тивление смежной ветви между первым и вторым контурами, взятое со знаком минус, Z_I2 = -R = -5; £, । — алгебраическая сумма ЭДС первого контура, £_{( (} = £\ = 100; Ё₂₂ — алгебраическая сумма ЭДС второго контура, £,, = -£₂ = -100 J.

Следовательно,

7_п (5-2;)-5/₂₂ = 100;

-5 /_п + /₂₂ (5+ 5» = -100/

Определитель системы

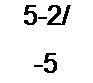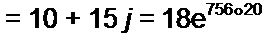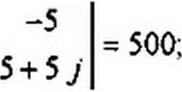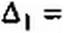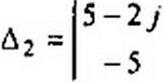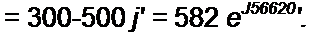Токи в схеме

/_п = Д|/Д = 500/18е^;56’²⁰' = 27,8 6''⁵⁶°²⁰' А;

/₂₂ = Д₂ /Д = 582 е-'⁵⁹⁶ /18е' ^5<™' = 32,3 е~' "⁵’²⁰‘ А;

4 = /„-/,, = 30е^у,1<М}.

Топографическая диаграмма изображена на рис. 3.20, б.

§ 3.21. Активная, реактивная и полная мощности. Под активной мощностью Р понимают среднее значение мгновенной мощности р за период Т:

1 г 1 г

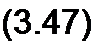Р = — \р dt - — ui dt.

Т J ^r T J

1 О 'о

Если ток / I_m sin со/, напряжение на участке цепи и = U,„ sin(co/ + ф), то

Р = — U_ni sin о/ sin(<of + <p) dt = —со5ф. (3.48) Г о 2

Активная мощность физически представляет собой энергию, которая выделяется в единицу времени в виде теплоты на участке цепи в сопро­
тивлении Я. Предполагается, что в I с укладывается целое число перио­дов Т. Действительно, произведение U cos<p = / Я. Следовательно,

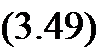Р = U cos<p / = /^[2] R.

Единица активной мощности — ватт (Вт).

Под реактивной мощностью Q понимают произведение напряжения U на участке цепи на ток / по этому участку и на синус угла ф между напряжением U и током / :

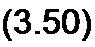Q = U 1 sin ф.

Единица реактивной мощности — вольт-ампер реактивный (ВАР). Если sin ф > 0, то 0>О, если 5шф<0, то Q<0.

Рассмотрим, что физически представляет собой реактивная мощность. С этой целью возьмем участок цепи с последовательно соединенными Я, £ и С. Пусть по нему протекает ток i = l„, sin со/. Запишем выражение для мгновенного значения суммы энергий магнитного и электрического по­лей цепи:

и/ w/ ы/ Си² Ll^.i С 2

^мэ = =------- +------ “ “ sm" ^{со/ +}------- ^cos =

^{МЭ м [3]} 2 2 2 2(w С)²

£ /² Z²

=------- (1 - cos 2и>г) +---- г— (1 + cos 2cor).

2 2 ar С

Из полученного выражения видно, что имеет постоянную составляющую ^_МЭ0’ неизменную во времени, и переменную составляю­щую и>_мэ изменяющуюся с двойной угловой частотой:

^мэ “ И'мэо “ ^WM3>

где

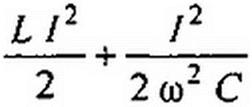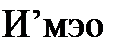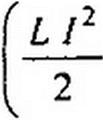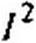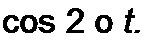На создание постоянной составляющей была затрачена энер­гия в процессе становления данного периодического режима. В дальней­шем при периодическом процессе энергия ^_МЗо остается неизменной и, следовательно, от источника питания не требуется энергии на ее со­здание.

Среднее значение энергии поступающей от источника за ин­

тервал времени / от -7/8 до +7/8,

/«778

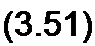^МЭ ср ~

Таким образом, реактивная мощность Q пропорциональна среднему за четверть периода значению энергии, которая отдается источником питания на создание переменной составляющей электрического и маг­нитного полей индуктивной катушки и конденсатора.

За один период переменного тока энергия Й^_МЭср дважды отдается ге­нератором в цепь и дважды он получает ее обратно, т. е. реактивная мощ­ность является энергией, которой обмениваются генератор и приемник.

Полная мощность

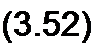S = U I.

Единица полной мощности — В • А.

Мощности Р, Q и S связаны следующей зависимостью:

P²+Q²=S². (3.53)

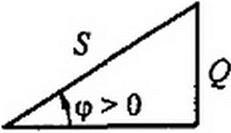
ически эту связь можно представить в виде прямоугольного тре­угольника (рис. 3.21) — треугольника мощности с катетами Р, Q и гипо­тенузой S'.

На щитке любого источника электрической энергии переменного тока (генератора, трансформатора и т. д.) указывается значение S, характеризующее ту мощ­ность, которую этот источник может отдавать потреби­телю, если последний работает при со$ф = 1 (т. е. если потребитель представляет собой чисто активное сопро­тивление).

§ 3,22. Выражение мощности в комплексной форме записи. Пусть задан некоторый комплекс

А = А е^7Фг = A cosq^ + j A sincp^.

Под комплексом А, сопряженным с комплексом А, будем понимать

А = А е"^/ф-' = A coscp ₄ - j A sinф_л.

Рассмотрим простой прием определения активной и реактивной мощ­ностей через комплекс напряжения и сопряженный комплекс тока. На­пряжение на некотором участке цепи U -U е^{у ф}*, ток по этому участку / = Z е^уф'. Угол между напряжением и током ф = (р_и -ф,.

_w Умножим комплекс напряжения на сопряженный комплекс тока / = / е'^УФг и обозначим полученный комплекс через S :

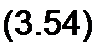S =(И = 1) /е^/(ф‘~^ф'⁾ = (J /е^УФ =

= U I созф + j U / sin ф = Р + j Q.

Значок - (тильда) над S обозначает комплекс (а не сопряженный ком­плекс) полной мощности, составленный при участии сопряженного ком­плекса тока /.

Таким образом, активная мощность Р есть действительная часть (Re), *

а реактивная мощность Q — мнимая часть (Im) произведения U I:

(3.55)

Пример 40. Определить активную, реактивную и полную мощности по данным при­мера 31.

Решение. Напряжение на входе всей схемы равно ЭДС 0 = £ = 100 В. Ток в цепи / = 17,2 е"^{7 31} А. Сопряженный комплекс тока 1 ~ 17,2 е^{7 31} А. Комплекс полной мощности S = I/ / = 100• 17.2 е^{7 31}° = i 720 cos31 ° + У 1720sin31° = 1475 + у 886; Р = 1475; Q = 886

Следовательно, активная мощность Р-1475 Вт, реактивная (7 = 886 ВАР и полная 5 = 1720 В А.

§ 3.23, Измерение мощности ваттметром. Измерение мощности производят обычно с помощью ваттметра электродинамической системы, в котором имеются две катушки — неподвижная и подвижная.

Подвижная катушка, выполненная из очень тонкого провода, имеет практически чисто активное сопротивление и называется параллельной обмоткой. Ее включают параллельно участку цепи, подобно вольтметру. Жестко скрепленная со стрелкой (указателем), она может поворачивать­ся в магнитном поле, создаваемом неподвижной катушкой.